A Study on the Optimization Algorithm for Correlation Analysis of the Underground Utility Structure Density in Urban Areas and Recorded Ground Subsidence

Changho Choi; Jin-Young Kim; Sung-Ha Baek; Jae Mo Kang

doi:10.7843/kgs.2021.37.10.77

Preview

Journal of the Korean Geotechnical Society. 31 October 2021. 77-87
https://doi.org/10.7843/kgs.2021.37.10.77

A Study on the Optimization Algorithm for Correlation Analysis of the Underground Utility Structure Density in Urban Areas and Recorded Ground Subsidence

도심지 지중매설물 밀집도와 이력지반함몰의 상관성 분석을 위한 최적화 알고리즘에 관한 연구

Changho Choi¹^*

Jin-Young Kim²

Sung-Ha Baek²

Jae Mo Kang²

최 창호¹^*

김 진영²

백 성하²

강 재모²

¹Member, Research Fellow, Korea Institute of Civil Engr. and Building Tech.

²Member, Senior Researcher, Korea Institute of Civil Engr. and Building Tech.

¹정회원, 한국건설기술연구원 지반연구본부 연구위원

²정회원, 한국건설기술연구원 지반연구본부 수석연구원

^{*Corresponding Author}

ABSTRACT

Several studies have been conducted to analyze, predict, and prevent the risk of ground subsidence occurring in urban areas. Nevertheless, there is insufficient research effort on risk analysis that utilizes the correlation between the density of underground structures (i.e., the spatial quantity of buried objects installed in the ground around the interested area) and the occurrence of ground subsidence. In this paper, a study was conducted to analyze the line density of underground structures using GIS-based spatial information data, and to link this with the recorded ground subsidences. An optimization algorithm was developed to maximize the correlation between the line density of 29 recorded ground subsidences and 6 types of underground structures that occurred between 2010 and 2015 for the analysis area. The concept of normalized line density was also proposed for the analysis. The normalized line density of the analysis area was divided into five grades (Grade 1: lowest, Grade 5: highest). When the optimization algorithm was applied, the case where the normalized line density was Grade 4 or higher at the location of the recorded ground subsidences was about > 80%. It is thought that the density analysis result of underground facilities can be applied to the ground subsidence risk analysis by using the proposed optimization algorithm.

Keywords

Ground subsidence

Optimization

Sinkhole

Underground structure

Utility pipeline density

도심지에서 발생하는 지반함몰의 위험도를 분석하고 예측 및 예방하기 위한 연구가 다양하게 진행되었다. 기존의 연구 중에 지하매설물의 밀도(즉, 대상 공간 주변 지중에 설치된 매설물의 공간적인 물량)와 지반함몰 발생의 상관성을 활용한 위험도 분석 연구는 미비하다. 본 논문에서는 GIS기반 공간정보 데이터를 활용하여 지하에 설치되어 있는 매설물의 선형밀도(line density)를 분석하고, 이를 이력지반함몰 발생 현황과 연계하는 연구를 수행하였다. 분석 대상 지역에 대하여 2010～2015년 사이에 발생한 29개 이력지반함몰과 6종 지하매설물 선형밀도의 상관관계를 극대화하기 위한 최적화 알고리즘을 개발하였고, 보편적인 분석을 위해 정규선형밀도의 개념을 제안하였다. 분석 대상 지역의 정규선형밀도를 5개 등급(1등급 최저, 5등급 최고)으로 구분하였으며, 최적화 알고리즘을 적용할 경우 이력지반함몰 위치에서 정규선형밀도가 4등급 이상인 경우가 약 80%이상으로 나타났다. 제안된 최적화 알고리즘을 활용하여 지하매설물의 밀집도 분석 결과를 지반함몰 위험도 분석에 적용할 수 있을 것으로 판단된다.

MAIN

1. 서 론
2. 공간정보 분석 지역 및 지하매설물 선형밀도 산정
2.1 공간정보 분석 지역
2.2 대상지역 선형밀도 분석
3. 이력지반함몰 데이터 기반 최적 정규선형밀도 분석 알고리즘
4. 이력지반함몰 데이터를 활용한 정규선형밀도 및 상관성 분석
4.1 이력지반함몰 데이터 기반 정규선형밀도 분석 결과
4.2 5개 등급 구분을 통한 이력지반함몰 데이터 분포
5. 결 론

1. 서 론

2014년에 발생한 석촌지하차도 하부의 대형 공동, 제 2 롯데월드 전면 도로에 발생한 지반함몰 등으로 인해 도심지에서 발생하는 지반침하에 대한 우려가 높아졌다. 정부는 선제적으로 지하안전관리체계를 구축하기 위해 지하안전관리에 관한 특별법을 제정하였고, 2018년부터 지반 굴착공사 전에 사업자가 지하안전영향평가를 실시하도록 하고 있다(Han, 2018). 도심지에서 발생하는 지반 침하 및 함몰 위험도를 예측하고 이를 방지하기 위한 다양한 연구가 진행되었다. Choi et al.(2016)과 Park et al.(2017)은 상하수도의 건전도 분석과 관로누수 및 결함을 감지하여 관로 주변에서 발생할 수 있는 지반함몰 위험도를 분석하고, 실시간으로 위험상황을 파악할 수 있는 시스템을 개발하였다. 또한, 대다수의 지반함몰이 하수관로의 결함, 구조상태 등과 관련이 있다는 데이터를 기반으로 하수관로의 설치 상태, 강우, 연식 등과 연계하여 지반함몰 위험도를 예측하는 연구가 수행되었다(Kim et al., 2018; Kwak et al., 2019). 서울시에서는 광역적 관점에서 지자체에서 보유하고 있는 GIS 기반의 매설물 위치정보와 기 발생한 지반함몰 또는 공동 위치의 이격거리 등의 상관관계를 분석하여 지반함몰 위험도를 분석하고자 하는 연구가 진행되었다(Seoul Metropolitan Government, 2017a). 지난 6년간 상기와 같은 다양한 연구가 진행되었으나, 현재까지 설치된 지하매설물의 밀도(즉, 대상 공간 주변에 설치된 지하매설물의 공간적인 물량)와 지반함몰 발생의 상관성에 기반한 위험도 분석 연구에 관한 것은 미비한 실정이다.

도심지 지하공간에는 다양한 매설물이 설치되어 있다. 대표적인 지하매설물은 상수도관로, 하수관로, 전력지중관로, 가스관로, 열배관, 통신관로 등이며, 대상 시설물은 공공 인프라이므로 주로 도로하부에 설치되어 있다. 지중의 관로는 도로를 개착하고 거치한 후 되메우기 하는 것이 일반적인 시공 방법이며, 시공 중에 하부지반을 교란한다. 다양한 관로가 복잡하게 설치되는 경우 굴착, 되메우기의 횟수가 증가하여 하부지반 토사의 교란도가 증가한다. 교란도가 높아지면 시간이 지남에 따라 지반침하 또는 지반함몰이 발생하는 빈도가 높아지는 것이 일반적인 사실이다. 대상 지역에서 지하매설물의 밀집도는 지반교란도와 밀접한 관계가 있으며, 상관성을 물리적으로 정량화하는 것은 어려우나 이력지반함몰과의 연계 분석을 통해 지반함몰의 위험도를 분석할 수 있을 것으로 판단된다.

본 연구에서는 국내 도심지의 GIS기반 공간정보 데이터를 활용하여 대상지역 하부에 설치되어있는 매설물의 선형밀도를 분석하고, 2010～2015년 사이에 발생한 이력지반함몰의 위치와 상관관계를 분석하였다. 1km×1km 대상 지역을 선정하여 6종 지하매설물의 선형밀도 데이터를 분석하고, 해당 지역에서 발생한 29건의 지반함몰 위치데이터와 공간상의 상관관계를 분석하였다. 선형밀도는 공간분석(spatial analysis)에서 활용되는 방법으로, 관심 셀 주위의 임의의 반경 내에 설치되어 있는 지하매설물 길이를 단위 면적당의 크기로 정의한다. 지하매설물에 따라 설치깊이, 직경, 기능 등이 상이하기 때문에 관심 셀에서 선형밀도는 임의의 반경내에서 각 매설물 길이별로 가중치를 설정하여 분석해야 한다. 본 연구를 통해 이력지반함몰 데이터와 지하매설물 선형밀도의 상관성을 높일 수 있는 가중치 분석을 수행하였으며, 가중치를 랜덤으로 생성하여 이력지반함몰 위치에서 선형밀도를 높게 분석할 수 있는 최적화 알고리즘을 개발하여 제안한다.

2. 공간정보 분석 지역 및 지하매설물 선형밀도 산정

2.1 공간정보 분석 지역

본 연구에서는 지하공간통합지도시스템에 구축되어 있는 데이터를 활용하여 지반함몰이 다수 발생한 구역을 분석 대상 지구로 선정하였다. 선정된 지역의 대형 지반함몰 발생 위치를 중심으로 1km×1km 격자를 생성 한 후 격자 안에 매설되어 있는 6종 지하매설물의 위치데이터와 지반함몰 이력 데이터를 추출하여 분석에 활용하였다. 계산된 선형밀도 래스터 파일을 분석에 활용하기 위해 셀 사이즈 10m로 격자를 나누고, 격자의 중심점에서 선형 밀도 값을 추출하여 지반함몰과의 상관성 분석에 활용하였다.

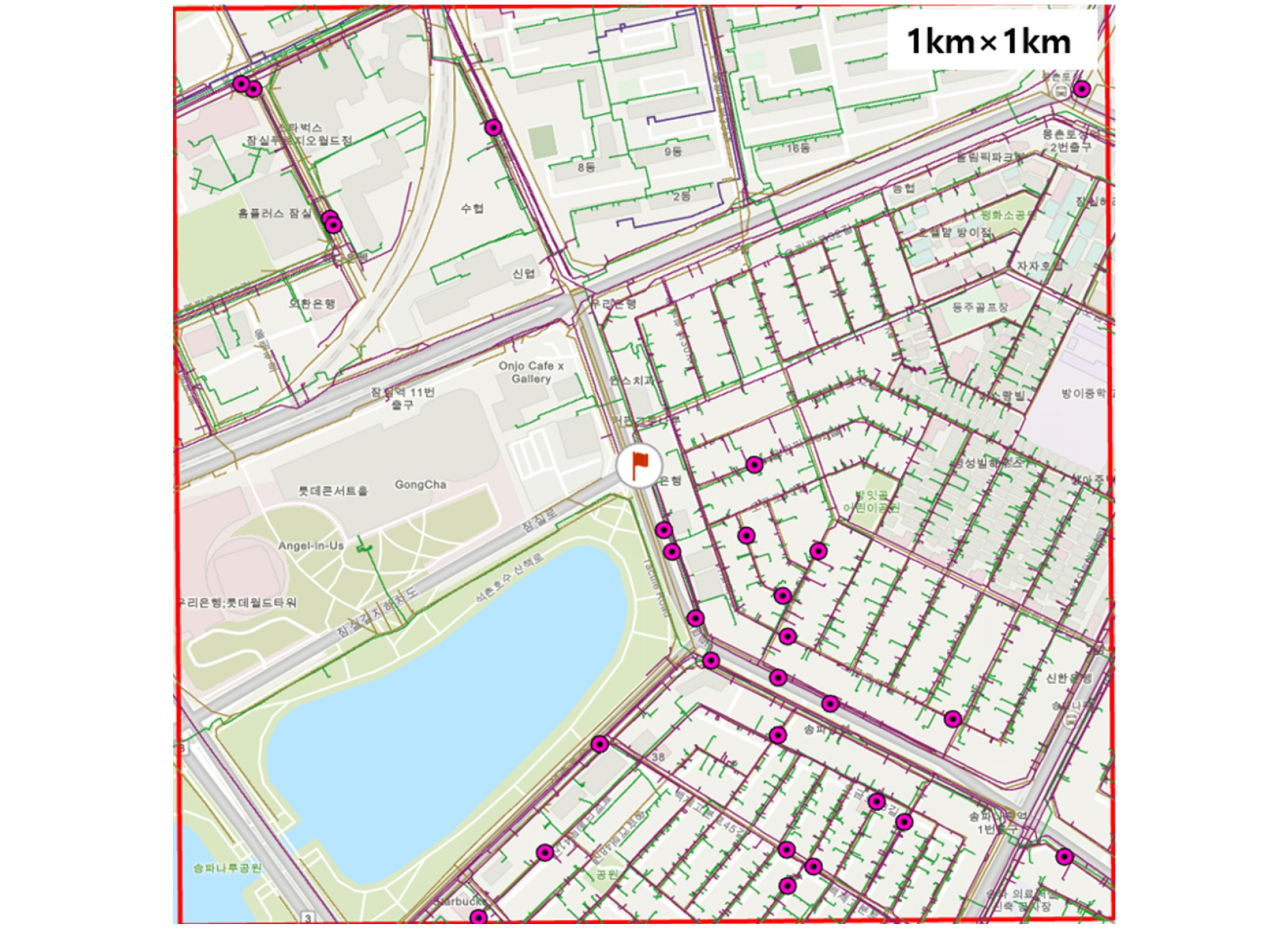
Fig. 1은 연구의 대상인 서울시 일부지역(1km×1km)의 맵을 보여주며, 맵 상에 빨간색 점들은 해당 지역에서 2010～2015 기간 동안 발생한 29개의 지반함몰 발생 위치를 보여준다. Table 1은 해당 지역에 설치된 6종 지하매설물(상수관로, 하수관로, 전력지중관로, 가스관로, 열 배관, 통신관로)의 총 설치길이와 단위 관로의 개수를 보여주고 있다. 각 매설물별 총 설치 길이는 상수관로(35,246m), 통신선로(34,443m), 천연가스관로(32,772m), 하수관로(26,630m), 전력지중관로(18,727m), 열배관(2,298m) 순으로 나타났다. 설치 길이로 보면 열배관의 길이는 타 매설물에 비해 매우 적은 것으로 나타났다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371007/images/kgs_37_10_07_F1.jpg

Fig. 1

1km×1km map of analysis region and 29 ground subsidence locations with magenta circle symbol

Table 1.

Length and number of unit for 6 buried utility structures

Buried structures	Total length (m)	No. of unit pipe (ea)	Avg. unit length (m)	Portion to total (%)
Water	35246	2840	12.41056	23.48
Sewer & Storm water	26630	873	30.50401	17.74
Power	18727	816	22.94975	12.48
Natural gas	32772	3363	9.744871	21.83
Heat	2298	28	82.07143	1.53
Communication	34443	636	54.15566	22.94
Total	150,116	8,556	-	100

2.2 대상지역 선형밀도 분석

지하공간에 설치된 매설물 밀집도는 해당 공간의 지반 토사의 교란도와 직접적인 관계가 있는 것으로 알려져 있다(Tokyo Metropolitan Government, 2012). 밀집도가 높다는 것은 해당 지역에서 개착 및 되메우기 시공이 다수 수행되었다는 것을 직간접적으로 나타낸다. 높은 밀집도는 지반의 안정성에 미치는 영향이 매우 크므로, 중장기적으로 지반침하 및 공동(cavity)을 발생시킬 확률이 높아지는 것이 일반적이다.

선형밀도는 ArcGIS에서 제공하는 공간분석 기능의 하나이다(ArcGIS, 2021a). 선형밀도(line density)는 각 단위 셀 주변의 선형으로 구성된 구조물의 밀도특성을 제시하며, 해당지역 내에 포함된 선의 공간적인 밀집 정도를 나타낼 수 있는 지표로 단위면적당 길이로 산정된다. Fig. 2는 셀(grid cell)별로 선형밀도(ρ)를 계산하는 개념을 보여준다. 개념적으로 원내에 위치하는 선들의 길이의 합을 산정하고 이를 원의 면적으로 나누어 선형밀도(ρ)를 계산한다. L1과 L2는 원 안에 설치되어 있는 2개 매설물의 공간상의 길이를 나타내며, 각 매설물의 특성에 따라 가중치 w₁과 w₂를 가정할 수 있다. 이때의 선형밀도(ρ)는 식 (1)을 통해 산정할 수 있다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371007/images/kgs_37_10_07_F2.jpg

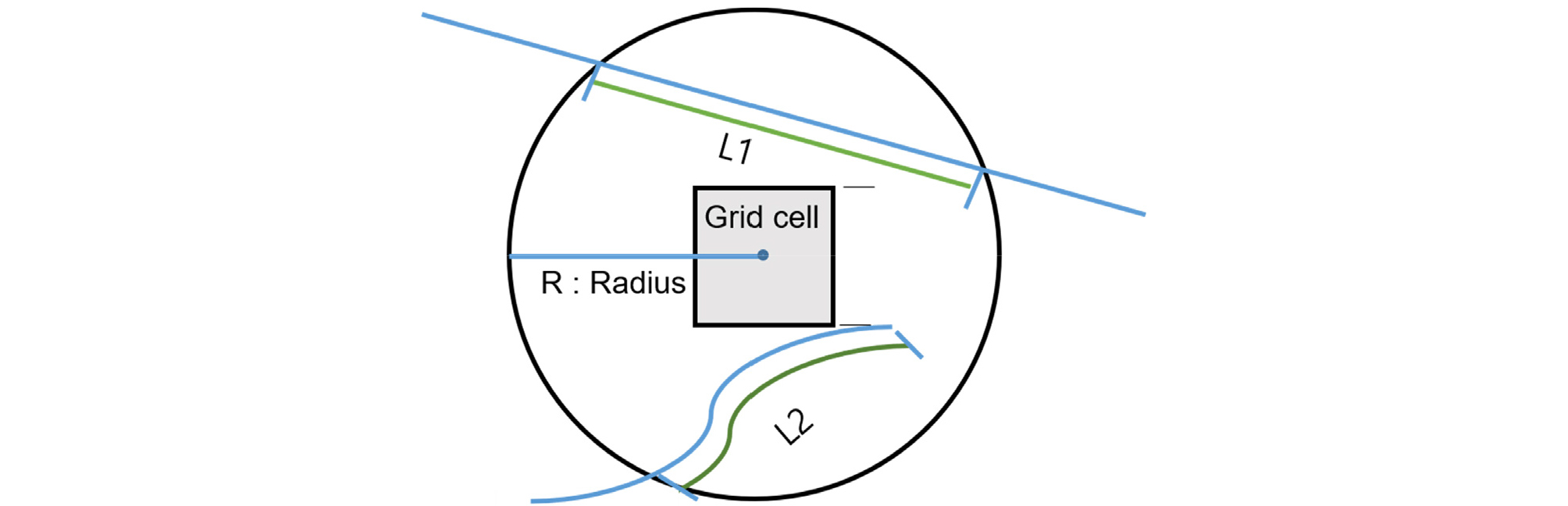
Fig. 2

A raster cell and the circular neighborhood used to determine the length for the line density (Redrawn from ArcGIS (2021a))

(1)

ρ = \frac{w_{1} L_{1} + w_{2} L_{2}}{A_{R}}

여기서, A_R은 해당셀에 영향을 미치는 원의 반지름 R로부터 계산된 원의 면적이다. ArcGIS에서 관로의 선형 밀도를 계산하기 위해서는 다선 특징(polyline features)이 있는 쉐이프파일(shape file)이 필요하다. Fig. 2와 식 (1)로부터 셀(grid cell)의 크기, R의 크기, 가중치 w₁, w₂를 결정해야 한다. A_R은 반지름의 제곱에 반비례하는 함수이므로, R이 커지면 일반적으로 선형밀도(ρ)가 $~ \frac{1}{O^{2}}$ 로 비례하여 감소하게 되나, 해당 구역 내에 관로의 길이가 증가하므로 도심지역의 특성에 따라 변화할 수 있다. 따라서 해당 지역의 특성을 분석하여 R을 결정하는 것이 중요한 요소이다.

식 (2)는 대상 지역의 지하매설물 선형밀도를 정규화하기 위해 활용될 수 있다.

(2)

ρ_{n} = \frac{w_{1} L_{1} + w_{2} L_{2} \dots + w_{n} L_{n}}{n \cdot A_{R}}

where, w₁, w₂, …w_n : weight factors L₁, L₂, …L_n : length of each buried structures

n : number of buried structure types

R : radius of affecting zone

(3)

\sum_{i = 1}^{n} w_{i} = 1.0

식 (2)에서 ρ_n(정규선형밀도)은 고려 대상의 지하매설물 종류의 개수로 정규화된 선형밀도 값이며, 대상지역의 정량적인 선형밀도는 ρ=n・ρ_n으로 산정할 수 있다. 식 (3)은 n개 매설물별 weight factor의 합이 1.0으로 제한됨을 의미한다.

Table 2는 선형밀도 분석에 활용하기 위해 ArcGIS로부터 산정한 3개의 Raw-data set를 정의하여 보여준다. x(1km)×y(1km) 대상지역에 대하여 셀사이즈를 10m로 설정하고, 3개의 Radius(해석반경)을 적용하여 데이터 세트를 구성하였다. 각각의 데이터 세트는 셀의 ID, x 및 y grid-ID와 6종 지하매설물(상수관, 하수관, 전력지중관, 천연가스배관, 통신선로, 열배관)의 개별 선형밀도, 지반함몰 발생 여부(1: 발생, 0: 미발생) 개수의 열(column)벡터로 구성되었다. 대상지역 경계에서는 선형밀도의 정확도를 향상시키기 위해 경계 외측에서도 R의 범위 내에 있는 매설물의 길이를 선형밀도 분석에 포함하였다.

Table 2.

Raw-data set used for line density analysis

Raw-data ID	Cell size (m)	Radius (m)	Range(m)
R50	10	50	x(1000)×y(1000)
R100		100
R150		150

* To obtain appropriate line densities in the x and y boundaries, outer pipelines within the range of R were considered in ArcGIS domain.

3. 이력지반함몰 데이터 기반 최적 정규선형밀도 분석 알고리즘

본 절에서는 식 (3)의 조건을 충족하고 Fig. 1의 지반함몰이 발생한 29개 위치에서 정규선형밀도가 높게 분석될 수 있도록 w₁, w₂…, w₆을 산정하는 방법을 제시한다. 이를 위해 $\sum_{i = 1}^{6} w_{i} = 1.0$ 의 제약조건(constraint)을 만족하는 6종의 매설물별로 w_i값을 랜덤으로 생성하였다. 설정된 간격에서 $\sum_{i = 1}^{6} w_{i} = 1.0$ constraint을 준용하여 무작위로 균일(uniform)한 벡터를 생성하는 알고리즘을 활용하였다(Stafford, 2021). 『Random Vectors with Fixed Sum』 알고리즘은 a≤w_i≤b의 공간에서 합이 s인 [w₁; w₂; w₃; …w_n] 값으로 구성된 m개의 임의 요소 열벡터를 생성한다. 생성된 벡터는 m-1차원 공간에 무작위로 균일하게 분포된다. 아래는 Matlab 코드의 function header를 보여준다.

function [w] = randomVectorsWithFixedSum(n,m,s,a,b)

여기서, return variable [w]=[n×m]의 매트릭스로 구성되며, n은 고려대상 지하매설물 종류의 개수이다.

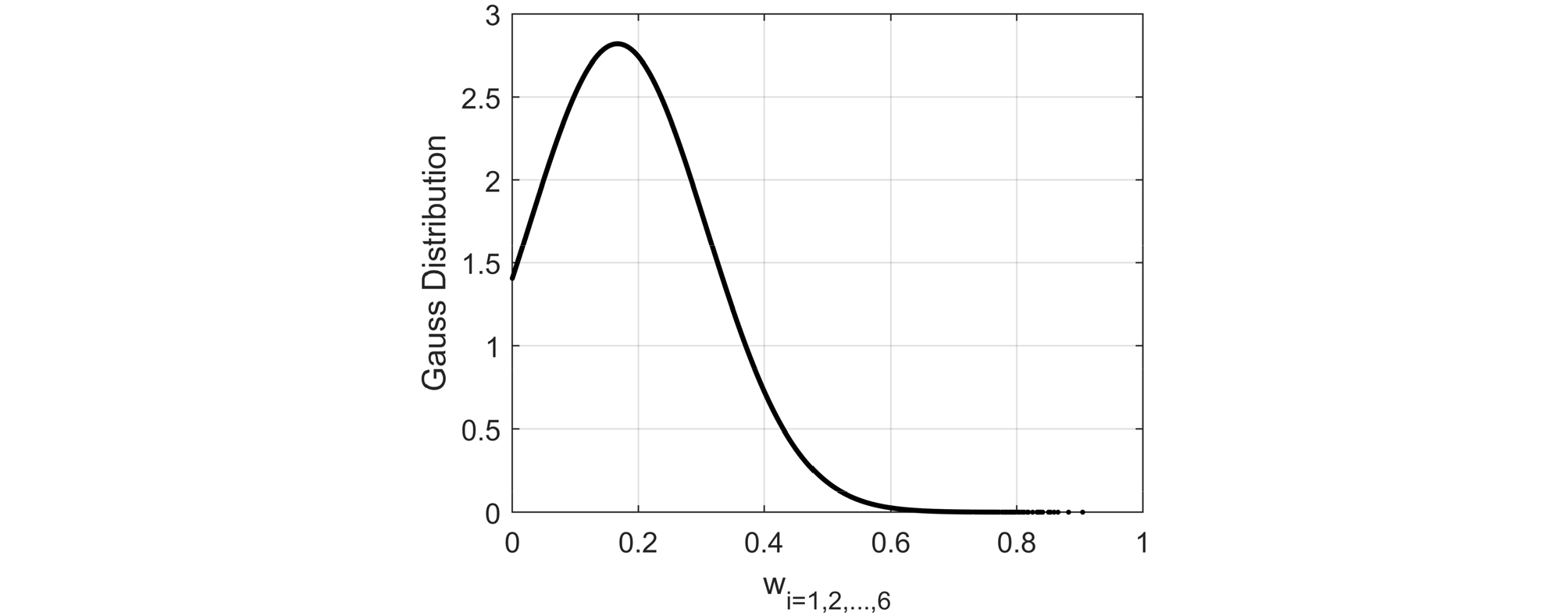
6종 지하매설물(상수관, 하수관, 전력지중관, 천연가스배관, 통신선로, 열배관)의 정규선형밀도 분석을 위해 『Random Vectors with Fixed Sum』 function을 활용하여 100,000세트의 w_i=[w₁; w₂; w₃; w₄; w₅; w₆]을 생성하였다. 즉, w₁, w₂, w₃, w₄, w₅, w₆은 각각 상수관, 하수관, 전력지중관, 천연가스배관, 통신선로, 열배관의 개별밀도의 가중치이다. Fig. 3은 랜덤으로 생성된 100,000개 w₁의 Gauss-distribution 커브를 예로 보여주며, w₂, w₃, w₄, w₅, w₆도 동일한 양상의 커브이다. Fig. 3에서와 같이 각 w_i=1,2,…,6 들은 1/6에 해당하는 0.167에서 곡선의 정점(peak)에 위치하고 가장 일어나기 쉬운 값이다. 즉, 6개의 지하매설물별로 1/6의 가중치를 가질 확률이 높다는 것을 의미한다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371007/images/kgs_37_10_07_F3.jpg

Fig. 3

Gauss distribution of randomly and uniformly distributed w₁, w₂, w₃, w₄, w₅, w₆ subjected to $\sum_{i = 1}^{6} w_{i} = 1.0$

Fig. 1에서 지반함몰이 발생한 29개 셀에 대하여, 상기의 100,000세트의 w_i=[w₁; w₂; w₃; w₄; w₅; w₆]를 적용하고 정규선형밀도를 산정하였다. 식 (4)는 지반함몰이 발생한 29개 셀의 정규선형밀도를 100,000세트의 랜덤 w_i=[w₁; w₂; w₃; w₄; w₅; w₆]로 산정하기 위한 일반식을 보여준다.

(4)

ρ_{n s} = ρ_{s h} \cdot w_{i}

여기서, ρ_ns: 지반함몰이 발생한 29개의 셀에서 정규선형밀도, ρ_sh: 지반함몰이 발생한 29개의 셀에서 선형밀도이다. Dot product •는 Matrix multiplication를 의미한다. ρ_ns는 w_i를 적용한 정규선형밀도로서, 본 해석에서는 29개의 위치에서 100,000의 개의 w_i-set(세트는 w₁~w₆의 6개의 벡터 값을 의미)를 적용하므로, [29×100,000]의 Matrix로 구현된다. 지반함몰이 발생한 지점의 ρ_n은 해석 구역에서 높은 값을 갖는다는 가정하에 최적화(optimization)을 위한 Error 함수를 제안하였다. 식 (5)는 100,000개의 w_i-set중 29개 이력지반함몰 위치에서 정규선형밀도의 Error 함수를 제시한다.

(5)

E r r^{k} = ||1 - N_{p s}^{k}||

where, $N_{ρ s}^{k} = \frac{ρ_{n s}^{k}}{M a x (ρ_{n}^{k})}$

식 (5)에서 Err^k는 k번째 w_i-set을 적용할 때 29개 지반함몰 발생위치에서 에러값의 Norm을 나타낸다. ρ^k_ns는 29개 지반함몰 발생위치에서 w^k_i를 적용할 때 정규선형밀도이며, ρ^k_n는 식 (6)과 같이 해석영역에 w^k_i를 적용할 경우의 정규선형밀도로서 최대값은 Max(ρ^k_n)로 정의된다. 즉, N^k_ρs은 지반함몰이 발생한 위치에서 w^k_i를 적용할 때 Max(ρ^k_n)으로 정규화된 선형밀도의 비율(0～1.0)로 정의된다.

(6)

ρ_{n}^{k} = ρ_{r a w} \cdot w_{i}^{k}

식 (6)의 ρ^k_n는 k번째 w_i를 ρ_raw(모든 셀에서 6종 매설물별 선형밀도)에 적용하여 구한 정규선형밀도이다. 식 (5)를 통해 100,000개의 Error Norm을 분석하고, 식 (7)을 통해 Error가 최소인 w_opt-set을 결정한다.

(7)

w_{o p t} = w_{i}^{k^{o p t}}

(8)

k^{o p t} = f i n d (M i n (E r r))

식 (8)의 k^opt는 100,000개의 w_i-set 중에서 식 (5)의 Err가 최소화 될 때의 인덱스로 정의된다. Table 3은 식 (4)～식 (8)을 구현하기 위한 Psuedo-code를 보여준다.

Table 3.

Pseudo-code to obtain optimal w_i-set for finding higher correlation between normalized line density and ground subsidence

Pseudo-code	Description
for k=1:100,000
$ρ_{n}^{k} = ρ_{r a w} \cdot w_{i}^{k}$	% ρ^k_n : normalized line density with k^th w_i-set % ρ_raw : line density obtained from ArcGIS % w^k_i : k^th w_i-set
$ρ_{n_{m a x}}^{k} = m a x (ρ_{n}^{k})$	% ρ^k_{n_max} : maximum scalar value of ρ^k_n
$ρ_{n s}^{k} = ρ_{s h} \cdot w_{i}^{k}$	% ρ^k_ns : normalized line density at the locations of ground subsidence % ρ_sh : line density at the locations of ground subsidence
$N_{ρ s}^{k} = \frac{ρ_{n s}^{k}}{ρ_{n_{m a x}}^{k}}$	% N^k_ρs: normalized ρ^k_ns with ρ^k_{n_max}
$E r r^{k} = n o r m (1 - N_{p s}^{k})$	% Err^k : error norm with k^th w_i-set
end
$k_{o p t} = f i n g (M i n (E r r))$	% k_opt : Index where Err is minimum
$w_{o p t} = w_{i}^{k_{o p t}}$	% w_opt : w_i-set at the index of k_opt

Fig. 4는 100,000개의 랜덤 w_i-set을 적용하여 식 (5)의 Error를 분석한 결과의 예를 보여준다. 그림에서와 같이 29개 지반함몰 위치에서 Error Norm값은 약 1.5～4.5에 위치하며, 별표로 표기된 w_i-set ID=33838(k^opt)에서 Error가 최소화되는 것으로 나타났다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371007/images/kgs_37_10_07_F4.jpg

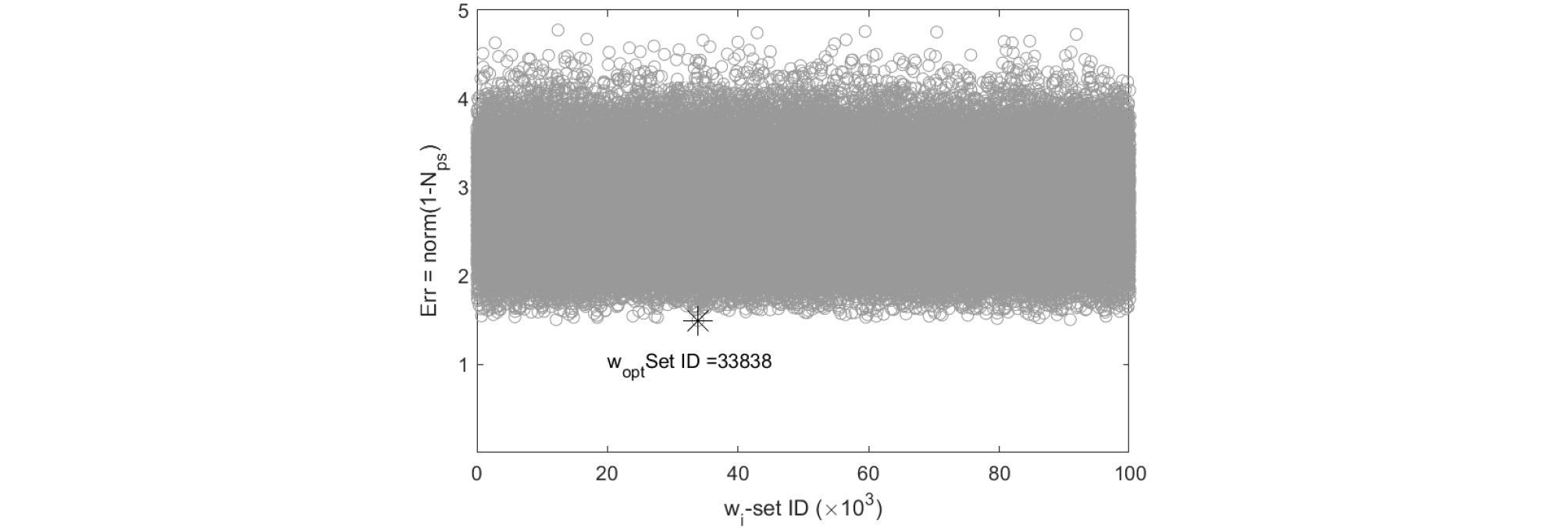
Fig. 4

Error analysis (Eq. (5)) for optimization of normalized line density with randomly created w_i-set for R50 case

4. 이력지반함몰 데이터를 활용한 정규선형밀도 및 상관성 분석

4.1 이력지반함몰 데이터 기반 정규선형밀도 분석 결과

본 절에서는 29개 이력지반함몰과 연구대상 지역의 정규선형밀도의 상관성 분석 결과를 제시한다. w_i=w₁, w₂, …, w₆=1/6와 w_i=w_opt를 적용하여 정규선형밀도를 분석하고 이력지반함몰의 위치에서 상관성을 분석하였다.

• w₁, w₂, …, w₆= $\frac{1}{6}$ 적용시 정규선형밀도와 이력지반함몰 상관성 분석 결과

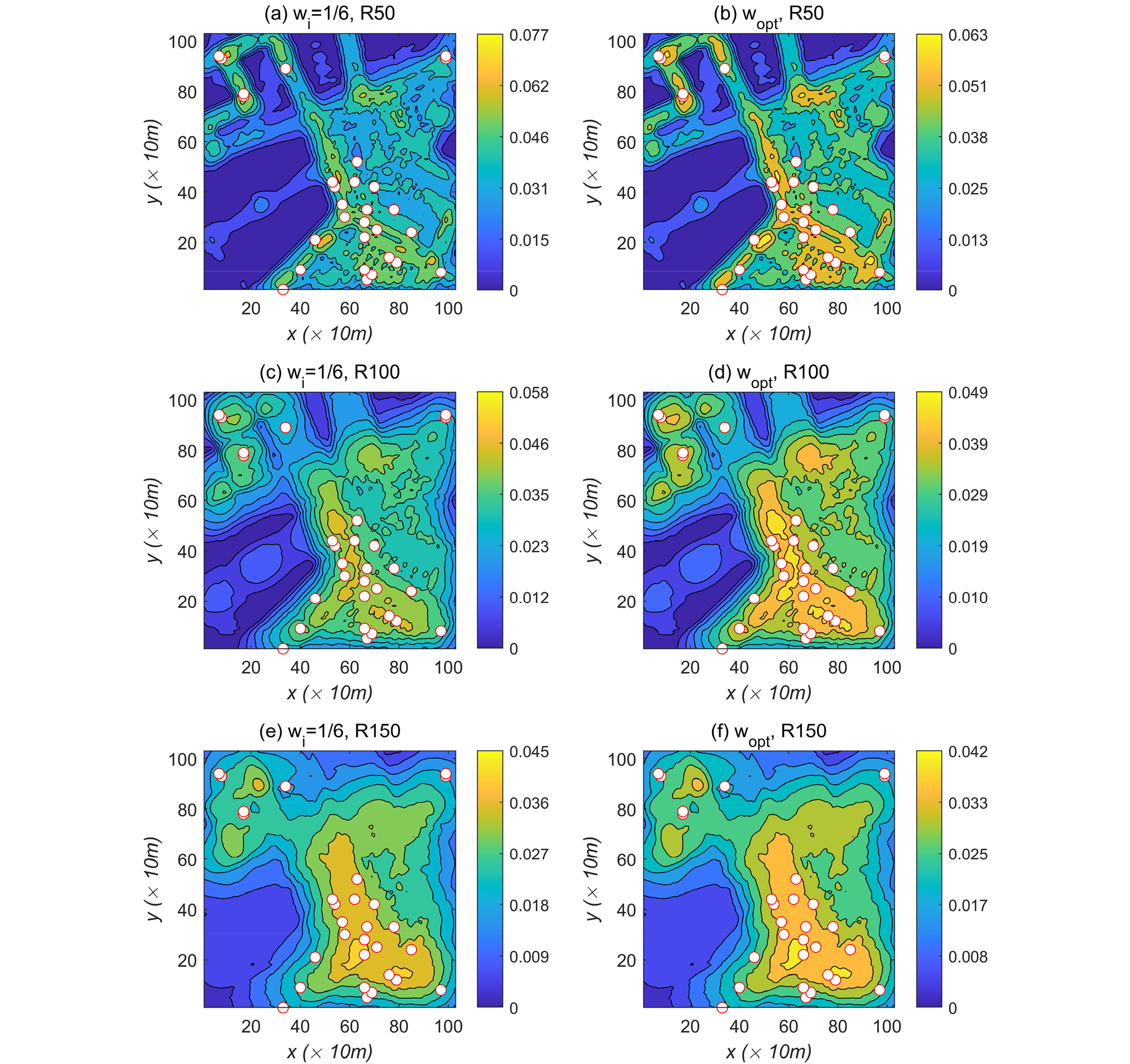
Fig. 5(a), 5(c), 5(e)는 각각 세 개의 R(50m, 100m, 150m)을 식 (2)에 적용하여 분석한 6종 지하매설물의 정규선형밀도(ρ_n)이다. 여기서, w₁, w₂, …, w₆=1/6로 동일하게 가정하였기 때문에 공간상에서 관로의 선(line) 정보만 고려된 경우이다. 그림에서 빨간색 원심볼은 29개의 지반함몰이 발생된 위치를 나타내며, 육안관찰로부터 정규선형밀도가 높은 지역에서 지반함몰이 상대적으로 많이 발생했음을 알 수 있다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371007/images/kgs_37_10_07_F5.jpg

Fig. 5

Comparison of ρ_n (normalized line density, m/m²) analysis results subjected to w₁, w₂, …, w₆=1/6(left column) and w_opt (right column) with R: 50m, 100m, 150m (colorbar represents 5 degrees of normalized line density for individual cases)

Table 4는 ρ_n의 최대값, 최소값, 평균값, 표준편차를 보여준다. ρ_n(m/m²)의 최대값은 R이 증가함에 따라 0.0774, 0.0581, 0.0449 순으로 감소하는 경향을 보여주었고, 평균값과 표준편차 모두 R의 증가에 따라 감소하였다.

Table 4.

Statistics of normalized line density (ρ_n) with the various R subjected to w_i=1/6 and w_opt

Weight factor	R50				R100				R150
Weight factor	Max	Min	Avg.	σ	Max	Min	Avg.	σ	Max	Min	Avg.	σ
w_i=1/6	0.0774	0	0.0238	0.0155	0.0581	0	0.0227	0.0117	0.0449	0.0017	0.0217	0.0097
w_opt	0.0635	0	0.0285	0.0180	0.0485	0	0.0260	0.0125	0.0418	0.0016	0.0236	0.0096

σ : Standard deviation

• w_opt 적용시 정규선형밀도와 이력지반함몰 상관성 분석 결과

무작위로 생성된 100,000 w_i-set를 Table 3의 최적화 알고리즘에 적용하여, 29개 지반함몰 위치에서 Error의 Norm값을 최소화하는 w_i-set를 분석하였다. Table 5는 최적화 알고리즘을 적용하여 분석한 R50, R100, R150 데이터 세트별로 w_opt값을 보여준다. 표에서 Err와 k는 각각 w_opt에서 식 (5)의 Error값과 100,000개의 랜덤 w_i-set중 최적 세트가 위치하는 인덱스이다.

Table 5.

w_opt out of 100,000 w_i-set obtained from minimizing Error function (Eq. (5)) with the variation of R

Radius (Cell 10m)	w_opt						Err=‖1-N_ps‖	k⁺
Radius (Cell 10m)	w₁ (Water)	w₂ (Sewer)	w₃ (Power)	w₄ (Gas)	w₅ (Comm)	w₆ (Heat)	Err=‖1-N_ps‖	k⁺
R50	0.2064	0.4107	0.0271	0.2851	0.0673	0.0034	1.4931	33838
R100	0.0202	0.6381	0.0012	0.2287	0.1007	0.0112	1.3595	24073
R150	0.0023	0.5529	0.0659	0.1861	0.1423	0.0505	1.6675	79685

⁺ Index out of 100,000 random w_i-set

Fig. 5(b), 5(d), 5(f)는 각각 세 개의 R(50m, 100m, 150m)에 대하여 w_opt을 식 (2)에 적용하여 분석한 6종 지하매설물의 정규선형밀도(ρ_n)이다. 그림에서 빨간색 원심볼은 29개의 지반함몰이 발생된 위치이다. 좌측의 w₁, w₂, …, w₆=1/6를 적용한 경우의 분석결과와 비교해보면 지반함몰이 발생한 위치에서 해당 분석 지역에서의 상대적인 정규선형밀도가 보다 높게 분포함을 알 수 있다. Fig. 5의 좌측과 우측의 해석결과 비교로부터, Table 3의 최적화 알고리즘이 대상 지역의 정규선형밀도를 산정하는데 적합하게 활용될 수 있음을 확인할 수 있다.

Table 4의 마지막 행은 w_opt적용시 ρ_n의 최대값, 최소값, 평균값, 표준편차를 보여준다. ρ_n(m/m²)의 최대값은 R이 증가함에 따라 0.0635→0.0485→0.0418로 감소하는 경향을 보여주었고, 평균값과 표준편차 모두 R의 증가에 따라 감소하였다. 표에서 w_i= $\frac{1}{6}$ 와 w_opt의 결과를 비교해보면, w_opt를 적용할 경우 ρ_n 최대값은 감소하고 평균값과 표준편차는 다소 증가하는 경향을 나타냈다. 향후 본 연구결과를 기초로 다양한 도심지역에서 셀크기 및 R변화에 따른 지하매설물 정규선형밀도의 영향을 분석할 필요가 있다.

4.2 5개 등급 구분을 통한 이력지반함몰 데이터 분포

Table 4의 w_i= $\frac{1}{6}$ 와 w_opt을 적용하여 산정한 정규선형밀도 통계결과의 최대 정규선형밀도를 바탕으로 밀도를 5개 등급으로 분류하였다. ArcGIS의 동일간격(Equal interval) 데이터 분류를 방법을 참고하여 5개 등급으로 설정하였다(ArcGIS, 2021b). 5개 등급은 ρ_{n_max}/5으로 나누어 G1(최저), G2, G3, G4, G5(최고)로 결정되며 등급이 높아질수록 지하매설물의 밀도가 상대적으로 높아지고 지반함몰 발생 위험도가 높아짐을 의미한다.

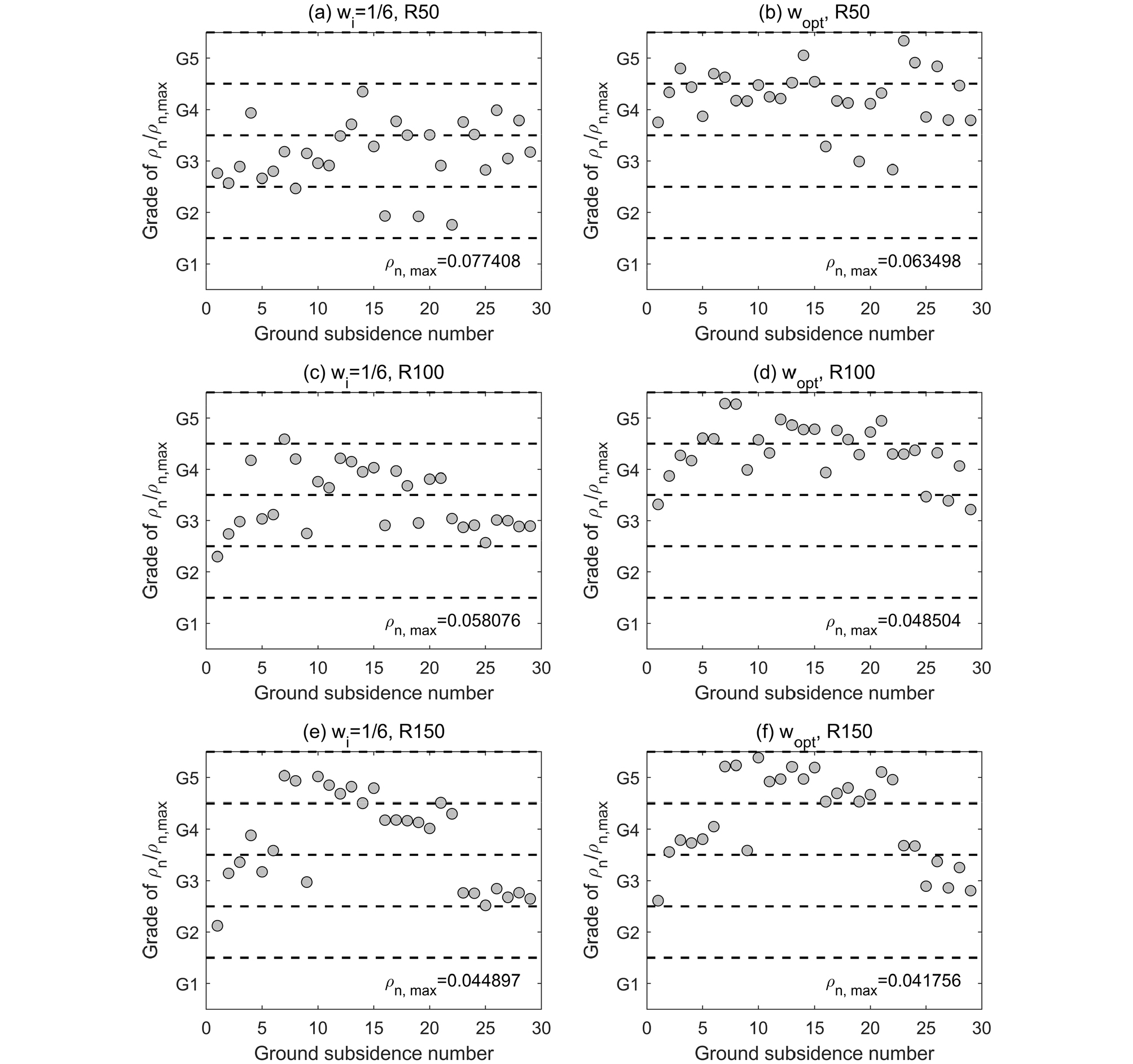
Fig. 6은 29개 이력지반함몰 위치에서 w_i= $\frac{1}{6}$ 과 w_opt를 적용한 정규선형밀도의 등급을 보여준다. 좌측열은 w_i= $\frac{1}{6}$ , 우측열은 w_opt을 적용한 해석결과이다. 각 열의 위에서부터 R은 각각 50m, 100m, 150m을 적용한 결과이다. 비교로부터 w_opt을 선형밀도분석에 적용할 경우 이력지반함몰이 일어난 위치에서 정규선형밀도의 등급이 상승하는 것을 볼 수 있다. 즉, 이력지반함몰 발생 위치에서 상대적인 지반함몰 위험도가 높다는 것을 의미한다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371007/images/kgs_37_10_07_F6.jpg

Fig. 6

Comparison of grades of $\frac{ρ_{n}}{ρ_{n, m a x}}$ at 29 sinkhole locations between w_i= $\frac{1}{6}$ (left column) and w_opt (right column) with R: 50m, 100m, 150m

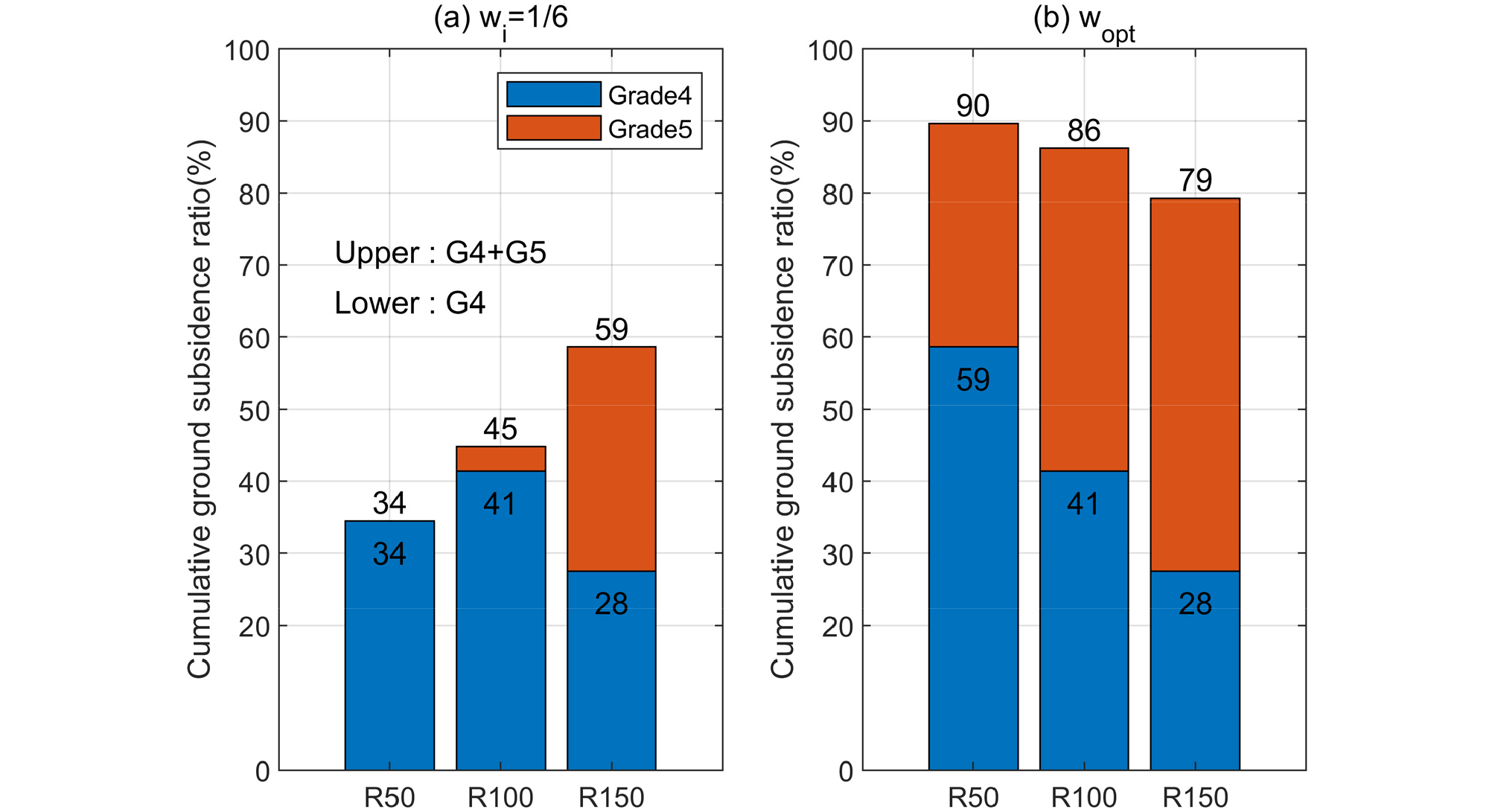
Table 6은 29개 이력지반함몰 위치에서 정규선형밀도를 분석하여 5개 등급별로 포함되는 함몰개수를 정리하여 보여준다. w_opt을 적용하여 정규선형밀도를 산정할 경우 모든 해석조건에서 29개 지반함몰은 3등급(G3) 이상의 값에서 발생한 것으로 나타났다. w_i= $\frac{1}{6}$ 을 적용한 경우에는 2등급(G2)에서도 다수의 지반함몰이 발생하였다. Fig. 7은 G4(파란색)와 G4+G5(빨간색) 등급에서 발생한 이력지반함몰의 비율을 그래프로 보여준다. w_i= $\frac{1}{6}$ 적용의 경우 R50: 34%, R100: 45%, R150: 59%, w_opt을 적용의 경우 R50: 90%, R100: 86%, R150: 79%의 이력지반함몰이 4등급(G4)이상의 정규선형밀도 지역에서 발생했음을 알 수 있다.

Table 6.

Number of ground subsidences corresponding to 5 grades at 29 sinkhole locations with w₁, w₂, …, w₆=1/6 and w_opt

Radius	R50		R100		R150
Grade	w_i=1/6	w_opt	w_i=1/6	w_opt	w_i=1/6	w_opt
G1	0	0	0	0	0	0
G2	4	0	1	0	1	0
G3	15	3	15	4	11	6
G4	10	17	12	12	8	8
G5	0	9	1	13	9	15
% (≥G4)	34	90	45	86	59	79

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371007/images/kgs_37_10_07_F7.jpg

Fig. 7

Cumulative percent and number of 29 sinkholes when ρ_n (normalized line density) ≥ Grade 4 along with R: 50m, 100m, 150m; (a) w_i= $\frac{1}{6}$ and (b) w_opt

Table 6과 Fig. 7은 본 연구의 최종 결과분석을 제시하였다. 본 연구를 통해 제안된 최적화 알고리즘을 적용하여 도출한 w_opt을 관심지역의 지하매설물 선형밀도분석에 적용하면, 지반함몰 위험도를 보다 정확하게 분석할 수 있음을 확인할 수 있다.

5. 결 론

본 논문에서는 GIS기반 공간정보 데이터를 활용하여 지하에 설치되어 있는 매설물의 선형밀도(line density)를 분석하고, 이를 지반함몰 위험도와 연계하는 연구를 수행하였다. 분석 대상 지역에서 2010～2015년 사이에 발생한 29개 이력지반함몰과 선형밀도의 상관관계를 최적화 할 수 있는 알고리즘을 개발하였고, 보편적인 분석을 위해 정규선형밀도의 개념을 제안하였다. 제안된 최적화 알고리즘을 적용하여 1km×1km 지역에 대한 정규선형밀도를 분석하고, 해당 지역에서 기 발생한 29건의 이력지반함몰 데이터와의 공간상의 상관관계 분석을 통해 정규선형밀도의 변화에 따른 지반함몰 발생 등급을 확인하였다. 본 연구를 통해 다음과 같은 주요 결론을 도출했다.

(1) 이력지반함몰과 6종 지하매설물 선형밀도의 상관성을 극대화하기 위한 연구를 수행하였다. 이를 위해 Constraint가 있는 Random Vector를 통해 6종 매설물에 최적의 weight factor를 산정하고, 정규선형밀도를 분석할 수 있는 최적화 알고리즘을 개발하였다. 최적화 알고리즘은 지반함몰이 발생하는 위치에서의 정규선형밀도가 높게 분포한다는 가정하에 개발되었다. 최적화 알고리즘을 적용할 경우 이력지반함몰 위치에서 정규선형밀도가 4등급(G4) 이상인 경우가 약 80% 이상으로 나타났고, 알고리즘의 적용이 적합함을 검증하였다.

(2) 본 논문에서는 도심지 일부 구간을 선정하여 최적화 알고리즘의 적용가능성을 검증하는데 초점을 맞추었다. 대상지역과 이력지반함몰의 데이터를 확장하여, 지하매설물의 밀도와 이력지반함몰과의 상관관계를 추가로 분석할 필요가 있다. 제안된 최적화 알고리즘을 활용하여 해석결과를 확장, 검증하면 도심지에서 지반함몰 위험도 지도를 구축하고 시설물 유지보수를 위한 의사결정 기초자료로 활용될 수 있을 것으로 판단된다.

Acknowledgements

본 연구는 한국건설기술연구원 (21주요-대1-임무) 지하공간 정보 정확도 개선 및 매설관 안전관리 기술개발(2/3) 지원으로 수행되었으며, 이에 깊은 감사를 드립니다.

References

ArcGIS(2021a), https://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-analyst-toolbox/how-line -density-works.htm

ArcGIS(2021b), https://desktop.arcgis.com/en/arcmap/10.3/map/working-with-layers/classifying -numerical-fields-for-graduated-symbols.htm

Choi, C., Kim, J., Kang, J., and Park, Y. (2016), "Ground Subsidence Risk Analysis with Intensity and Duration of Rainfall", Proc. of 3rd International Conference on Geotechnics for Sustainable Infrastructure Development, GEOTEC HANOI 2016 in Hanoi, Vietnam. 10.15341/mese(2333-2581)/03.03.2017/003

Han, Y. (2018), "Proposal of the Development Direction on the Special Act on Underground Safety Management for Preparation of the Proactive Underground Safety Management System", Journal of the Korean Geotechnical Society, Vol.34, No.7, pp.17-27.

Kim, K., Kim, J., Kwak, T-Y., and Chung, C-K. (2018), "Logistic Regression Model for Sinkhole Susceptibility due to Damaged Sewer Pipes", Natural Hazards, Vol.93, pp.765-785. 10.1007/s11069-018-3323-y

Kwak, T-Y, Chung, C-K, Kim, J., Lee, M., and Woo, S-I (2019), "Experimental Assessment for the Effect of Burial Depth on the Formation of Underground Cavities and Ground Cave-ins by Damaged Sewer Pipes", Journal of the Korean Geotechnical Society, Vol.35, No.11, pp.37-49.

Park, S., Kwak, P., Lee, H., and Choi, C. (2017), Development of Leakage Test Facility for Leak Signal Characteristic Analysis in Water Pipeline, Journal of Korean Society of Water and Wastewater, Vol.31, No.5, Oct. 2017. 10.11001/jksww.2017.31.5.459

Seoul Metropolitan Government (2017a), Development of road management big-data system, Project report (Step 1). Report No. 201705-PJ4-3-2.

Seoul Metropolitan Government (2017b), Seoul paved-road management system, https://pave.eseoul.go.kr, limited access to public.

Stafford, R. (2021), "Random Vectors with Fixed Sum", https://www.mathworks.com, MATLAB Central File Exchange.

Tokyo Metropolitan Government (2012), Survey results of situation of excavation about cavity below the road surface, Bureau of Construction,

UGS (2017), Urban buried structure monitoring and management system based on IoT (Internet of Things), Final Report. NST Combined Research Program.

Journal of the Korean Geotechnical Society ISSN:1229-2427(Print) 2288-646X(Online) 한국지반공학회 논문집

Preview

A Study on the Optimization Algorithm for Correlation Analysis of the Underground Utility Structure Density in Urban Areas and Recorded Ground Subsidence

ABSTRACT

MAIN

Fig. 1

1km×1km map of analysis region and 29 ground subsidence locations with magenta circle symbol

Table 1.

Length and number of unit for 6 buried utility structures

Fig. 2

A raster cell and the circular neighborhood used to determine the length for the line density (Redrawn from ArcGIS (2021a))

(1)

(2)

(3)

Table 2.

Raw-data set used for line density analysis

Fig. 3

Gauss distribution of randomly and uniformly distributed w1, w2, w3, w4, w5, w6 subjected to ∑i=16wi=1.0

(4)

(5)

(6)

(7)

(8)

Table 3.

Pseudo-code to obtain optimal wi-set for finding higher correlation between normalized line density and ground subsidence

Fig. 4

Error analysis (Eq. (5)) for optimization of normalized line density with randomly created wi-set for R50 case

Fig. 5

Comparison of ρn (normalized line density, m/m2) analysis results subjected to w1, w2, …, w6=1/6(left column) and wopt (right column) with R: 50m, 100m, 150m (colorbar represents 5 degrees of normalized line density for individual cases)

Table 4.

Statistics of normalized line density (ρn) with the various R subjected to wi=1/6 and wopt

Table 5.

wopt out of 100,000 wi-set obtained from minimizing Error function (Eq. (5)) with the variation of R

Fig. 6

Comparison of grades of ρnρn,max at 29 sinkhole locations between wi=16 (left column) and wopt (right column) with R: 50m, 100m, 150m

Table 6.

Number of ground subsidences corresponding to 5 grades at 29 sinkhole locations with w1, w2, …, w6=1/6 and wopt

Fig. 7

Cumulative percent and number of 29 sinkholes when ρn (normalized line density) ≥ Grade 4 along with R: 50m, 100m, 150m; (a) wi=16 and (b) wopt

Acknowledgements

References

Gauss distribution of randomly and uniformly distributed w₁, w₂, w₃, w₄, w₅, w₆ subjected to $\sum_{i = 1}^{6} w_{i} = 1.0$

Pseudo-code to obtain optimal w_i-set for finding higher correlation between normalized line density and ground subsidence

Error analysis (Eq. (5)) for optimization of normalized line density with randomly created w_i-set for R50 case

Comparison of ρ_n (normalized line density, m/m²) analysis results subjected to w₁, w₂, …, w₆=1/6(left column) and w_opt (right column) with R: 50m, 100m, 150m (colorbar represents 5 degrees of normalized line density for individual cases)

Statistics of normalized line density (ρ_n) with the various R subjected to w_i=1/6 and w_opt

w_opt out of 100,000 w_i-set obtained from minimizing Error function (Eq. (5)) with the variation of R

Comparison of grades of $\frac{ρ_{n}}{ρ_{n, m a x}}$ at 29 sinkhole locations between w_i= $\frac{1}{6}$ (left column) and w_opt (right column) with R: 50m, 100m, 150m

Number of ground subsidences corresponding to 5 grades at 29 sinkhole locations with w₁, w₂, …, w₆=1/6 and w_opt

Cumulative percent and number of 29 sinkholes when ρ_n (normalized line density) ≥ Grade 4 along with R: 50m, 100m, 150m; (a) w_i= $\frac{1}{6}$ and (b) w_opt