1. 서 론
2. 연구대상 지역
3. 시험방법
3.1 표준관입시험(SPT) 및 다운홀테스트(Downhole test)
3.2 화학적 풍화지수
4. 데이터 분석방법 및 결과
4.1 분석자료
4.2 비선형 다변량 회귀분석
5. 결 론
1. 서 론
화강암은 국내 지반의 대표적인 암종이며 풍화토와 풍화암을 포함하는 화강 풍화대 지반은 대부분의 주요 건설공사에서 지반구조물의 지지층으로 활용되고 있으므로 화강 풍화대의 지반특성 및 지반정수를 평가하는 것은 구조물의 성능과 안전성 확보를 위해 중요하다.
풍화대 지반은 시료 채취 시 실내시험에 적합한 불교란 시료를 충분히 확보하기 어렵기 때문에 일반적으로 현장시험을 통해 지반특성을 평가하며, 풍화대 지반의 강도특성 및 변형특성과 관련된 연구가 활발히 진행되어 왔다(Lee and Jang, 2003; Sun et al., 2006; Choi et al., 2010). 특히, 최근 경주, 포항 지진으로 인해 내진설계의 중요성이 부각되고 있음에 따라 다양한 공학적 특성 중에서도 풍화대 지층의 분류, 내진설계 시 지반분류 및 지반 최대 전단 탄성계수(Gmax) 평가에 활용되는 전단파 속도(VS)의 합리적인 평가의 중요성이 증가하고 있다.
전단파 속도(VS)는 SASW(Spectra Analysis of Surface Waves), 다운홀(downhole), 업홀(uphole), 크로스홀(crosshole) 등 다양한 현장 탄성파 탐사를 통해 평가할 수 있으며, 국내에서 수행된 현장 탄성파 시험 결과를 바탕으로 전단파 속도 평가에 대한 연구가 활발히 수행되어 왔다(Sun et al., 2006, 2007, 2008; Do et al., 2011; Kim et al., 2014). 현장 탄성파 탐사는 지층의 전단파 속도를 비교적 정확히 평가할 수 있는 장점이 있으나, 비용과 시간의 제약으로 인해 제한적으로 수행되고 있는 실정이다. 이에 기존 연구자들은 비교적 간편하고 경제적인 표준관입시험(SPT: standard penetration test) 결과 N값을 이용하여 전단파 속도를 평가하기 위한 연구를 수행하였다. Sun et al.(2006)은 홍성 지역 풍화대를 대상으로 전단파 속도와 N값 간의 상관관계를 분석하였고, 다양한 화학적 풍화지수와 전단파 속도의 상관관계를 제시한 바 있으나, N값과 화학적 풍화지수 각각을 단일 독립변수로 하는 단순 회귀분석만을 수행하였다. Sun et al.(2008)은 국내 8개 지역에서 수행한 시험 결과를 바탕으로 전단파 속도와 N값 간의 상관관계를 지반분류에 따라 제시하였고, Jung et al.(2009)에서는 전국 227개 현장에서 측정한 전단파 속도와 N값을 바탕으로 지역별, 지층별 전단파 속도와 N값의 상관관계를 제안하였다. Do et al.(2011)은 충청지역을 대상으로 점성토, 사질토, 자갈, 풍화토, 풍화암층의 전단파 속도와 N값의 상관관계를 제시하였고, 기존 연구에서 제안된 국내 지반의 전단파 속도-N값 관계와 비교, 분석하였다. 그러나, 기존 연구에서는 N값만을 변수로 하는 단순회귀분석을 수행하여 전단파 속도의 추정식을 제시하였으며, 대부분의 국내 연구에서는 풍화대 지반정수에 중요한 영향을 미치는 풍화도를 고려하지 않았다. 또한, 국내 선행연구에서 제시한 전단파 속도-N값 상관관계의 결정계수(R2)는 0.165~0.342로 비교적 약한 상관관계를 보여, 실무적인 활용을 위해서는 풍화대 전단파 속도의 영향 인자를 추가적으로 고려하여 상관성을 높일 필요가 있다.
풍화대는 신선암이 풍화작용을 받아 생성되는 지층으로 풍화도는 풍화대의 공학적 특성에 영향을 미친다. 풍화에 따른 암의 공학적 특성 변화에 주목하여 국내외에서 풍화도와 암의 공학적 특성에 관한 연구가 활발히 수행되어 왔다. 특히, 암 구성 광물의 화학적 조성 변화를 바탕으로 풍화도를 정량적으로 평가할 수 있는 화학적 풍화지수를 산정하고, 암의 공학적 특성과 상관성 분석을 수행한 연구가 주를 이루었다(Chiu and Ng, 2014; Dearman et al., 1978; Gupta and Rao, 2001; Rigopoulos et al., 2015; Udagedara et al., 2017). 이는 화학적 풍화지수가 소량의 시료를 분석하여 풍화도를 평가할 수 있기 때문이다. 특히, 풍화대의 경우 별도의 시료 채취 과정을 거치지 않고 현장 표준관입시험 시 채취되는 시료를 사용할 수 있으므로 현장 적용성이 우수하다. Sun et al.(2006)은 홍성 지역 화강 풍화대를 대상으로 수행한 탄성파 탐사 및 표준관입시험 결과와 다양한 화학적 풍화지수를 분석하였으며, 국내 화강 풍화대에 대한 Vogt’s ratio(VR)의 공학적 활용성을 제시한 바 있으며, Lee(2020)는 화학적 풍화지수를 사용한 화강 풍화암의 지반정수 평가 시 VR의 적용성을 제시한 바 있다.
본 연구에서는 국내 화강 풍화대에 대한 사례 연구로 N값과 Sun et al.(2006)과 Lee(2020)의 연구에서 국내 화강 풍화대의 지반정수 평가에 적용성을 확인한 대표적인 화학적 풍화지수인 VR를 이용하여 전단파 속도를 평가할 수 있는 관계식을 제안하였다. 3개 현장에서 수행한 SPT, 다운홀 결과를 이용하였고, N값과 VR를 변수로 하는 비선형 다변량 회귀분석을 수행하였으며, 분석 결과로 도출된 전단파 속도 추정식을 선행 연구 결과와 비교 분석하였다.
2. 연구대상 지역
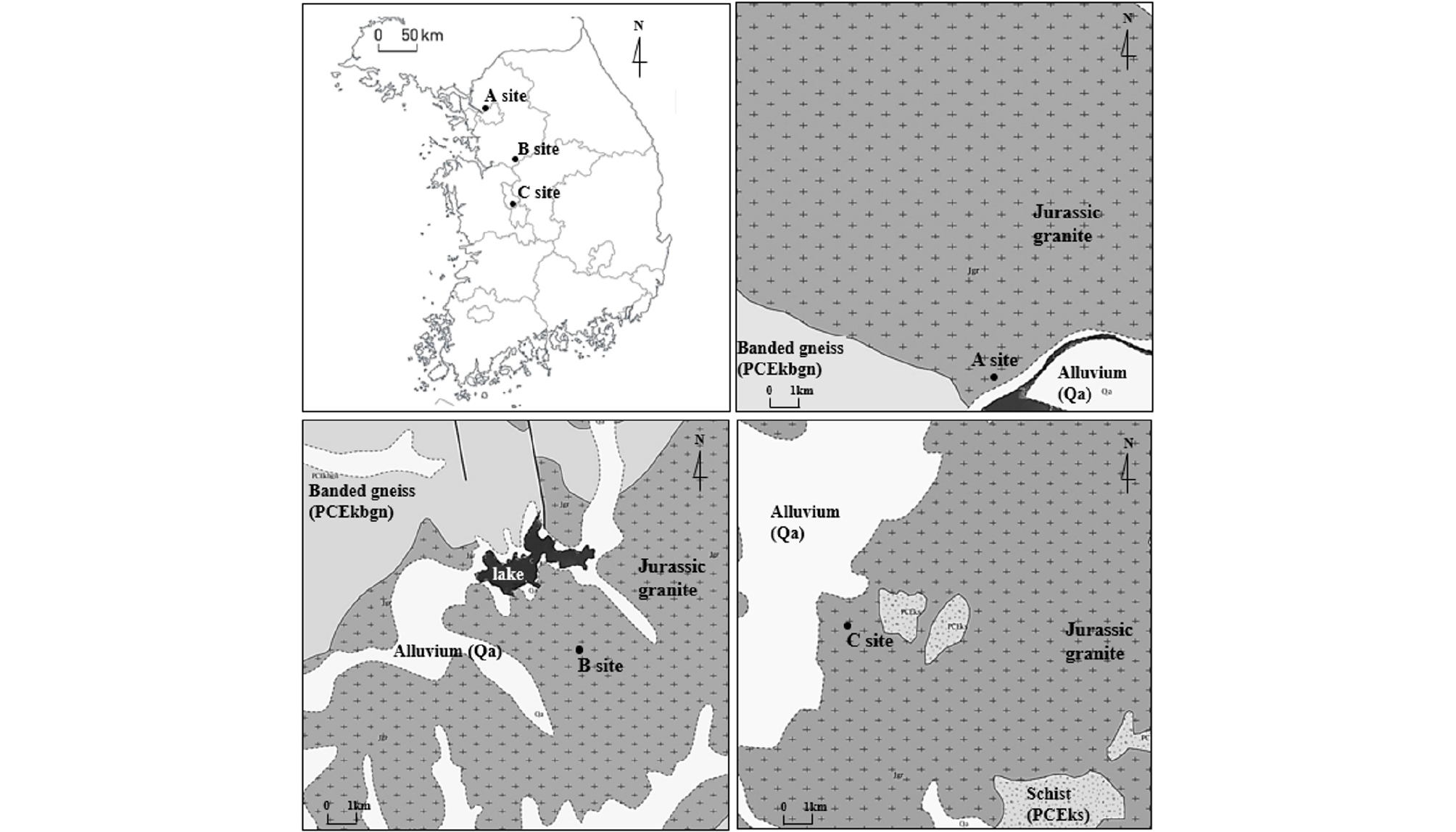
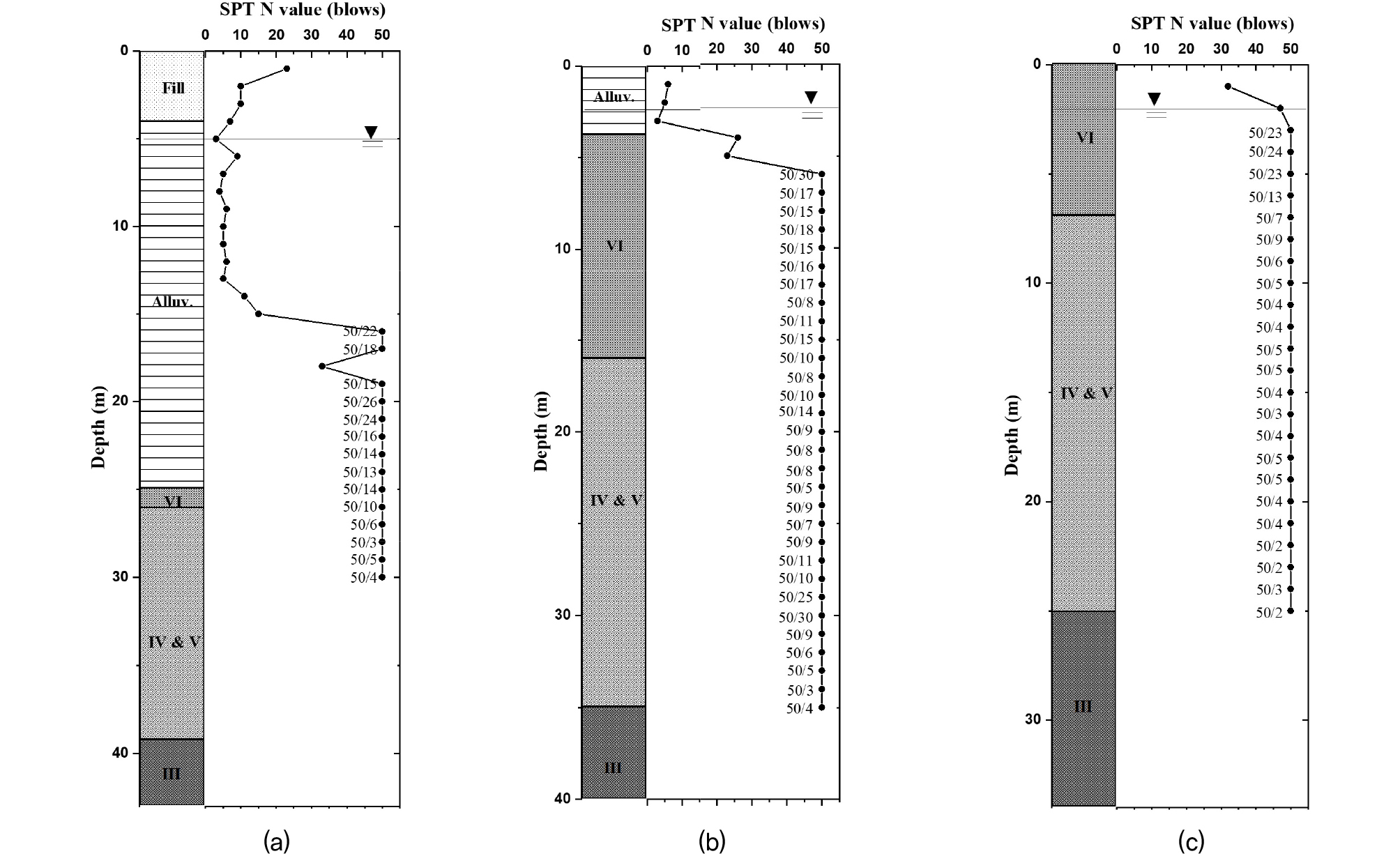
본 연구는 국내 중서부 지역의 3개 현장을 대상으로 수행되었다(Fig. 1). 3개 현장 모두 쥬라기 화강암 지역이며, 시추조사를 수행한 결과 풍화대는 A, B, C 현장에서 각각 14m, 25m, 23m로 두껍게 발달하였다(Fig. 2). A 현장은 강 하구 인접지역으로 풍화대 상부에 충적층이 매우 두껍게 발달되어 있었으며, B 현장은 인접한 소하천 지류의 영향으로 충적층이 약 3m 정도로 형성되어 있었다. 반면, C 현장은 구릉지역으로 퇴적작용이 발생할 지역적 요인이 없어 지표에서부터 풍화대가 발달하였다. 각 현장에서 표준관입시험(SPT: Standard Penetration Test)과 다운홀테스트(Downhole test)를 수행하였으며, 채취된 시료를 사용하여 화학적 풍화지수를 평가하였다. 상세한 시험 방법 및 획득한 데이터는 3장 및 4장에서 다루었다.
3. 시험방법
3.1 표준관입시험(SPT) 및 다운홀테스트(Downhole test)
표준관입시험은 ASTM D1586의 규정을 준수하여 수행하였으며 예비타(초기 15cm 관입 시 타격수)를 제외한 본타의 합(30cm 관입 시 타격횟수)을 측정하였다. 50타 이상의 타격 시 30cm 미만의 관입량이 측정되는 경우 50타에 해당하는 관입량을 측정하였으며, 연속된 10회의 타격에도 관입량이 발생하지 않는 경우 SPT를 종료하였다. 50타 타격 후 관입량이 30cm 미만으로 측정되는 경우 국내 유사 연구를 참고하여 본 연구에서는 측정된 N값을 선형 외삽하여 30cm 관입 시 타격수로 환산하여 분석에 활용하였다(Sun et al., 2006; Sun et al., 2008; Jung et al., 2009; Do et al., 2011). N값을 이용한 지반정수 추정 시 신뢰도 확보를 위해 에너지 효율, 연직유효응력, 시추공 직경, 샘플러 종류, 롯드 길이 등과 관련된 보정을 수행하여야 한다. 하지만 실질적으로 모든 인자에 대한 보정을 수행하기 어려우므로 현장 측정 N값을 사용하는 경우가 빈번하며, 국내에서 수행된 다수의 연구에서도 전단파 속도와 N값의 상관관계 분석 시 현장 측정 데이터의 활용성을 확보하기 위해 보정하지 않은 N값을 사용한 바 있다(Sun et al., 2006, 2008; Do et al., 2011). 본 연구에서는 N값 보정 중 가장 중요한 인자인 에너지 전달율을 고려하여 에너지 효율 60%에 상응하는 N60으로 보정하고 분석에 활용하였다.
다운홀은 OYO사의 장비를 이용하여 수행하였으며, 지표에서 대형 해머를 사용하여 압축파와 전단파를 발생시키며 시추공 내에서 1m 심도 간격으로 수신된 탄성파를 측정하였다. 탄성파의 전파 거리와 수신파와 발신파의 시간 차이를 이용하여 전단파 속도를 평가하였다. 다운홀을 이용한 전단파 속도의 상세한 평가 과정은 ASTM D7400에 상세히 기술되어 있다.
3.2 화학적 풍화지수
화학적 풍화지수는 풍화에 따라 변화하는 암의 주요 산화물의 함량비를 바탕으로 제안된 것으로 채취된 시료에 대한 X선 형광분석(XRF: X-ray fluorescence)을 통해 산정된다. 화학적 풍화지수는 시료의 물리적인 교란과 상관없이 풍화도를 평가할 수 있으므로 시료 채취 시 쉽게 파쇄되는 풍화대의 풍화도를 평가하기에 적합하다. 본 연구에서는 3개 현장의 표준관입시험 및 다운홀테스트가 수행된 심도에서 채취된 화강 풍화대 시료를 활용하여 XRF 분석을 수행하였으며, 분석 결과인 주요 산화물의 함량비를 몰비(molecular ratio)로 환산하여 화학적 풍화지수를 산정하였다. 다양한 화학적 풍화지수가 제안되어 있으나(Vogt, 1927; Ruxton, 1968; Vogel, 1975; Nesbitt, 1979; Irfan, 1996), 국내 화강 풍화대의 전단파 속도 등 지반정수 평가에 Vogt’s ratio(VR) 적용성이 제시된 바 있다(Sun et al., 2006; Lee, 2020). 본 연구에서는 선행 연구를 참고하여 대표적인 화학적 풍화지수인 VR(식 (1))를 화강 풍화대의 풍화도를 평가하는 지표로 활용하였다. VR은 알칼리 산화물과 알칼라인 산화물의 풍화에 따른 이동성을 바탕으로 제안된 화학적 풍화지수로, 풍화가 진행될수록 알칼리 산화물과 알칼라인 산화물의 함량비가 감소하므로 VR은 증가하는 이론적 경향을 보인다.
4. 데이터 분석방법 및 결과
4.1 분석자료
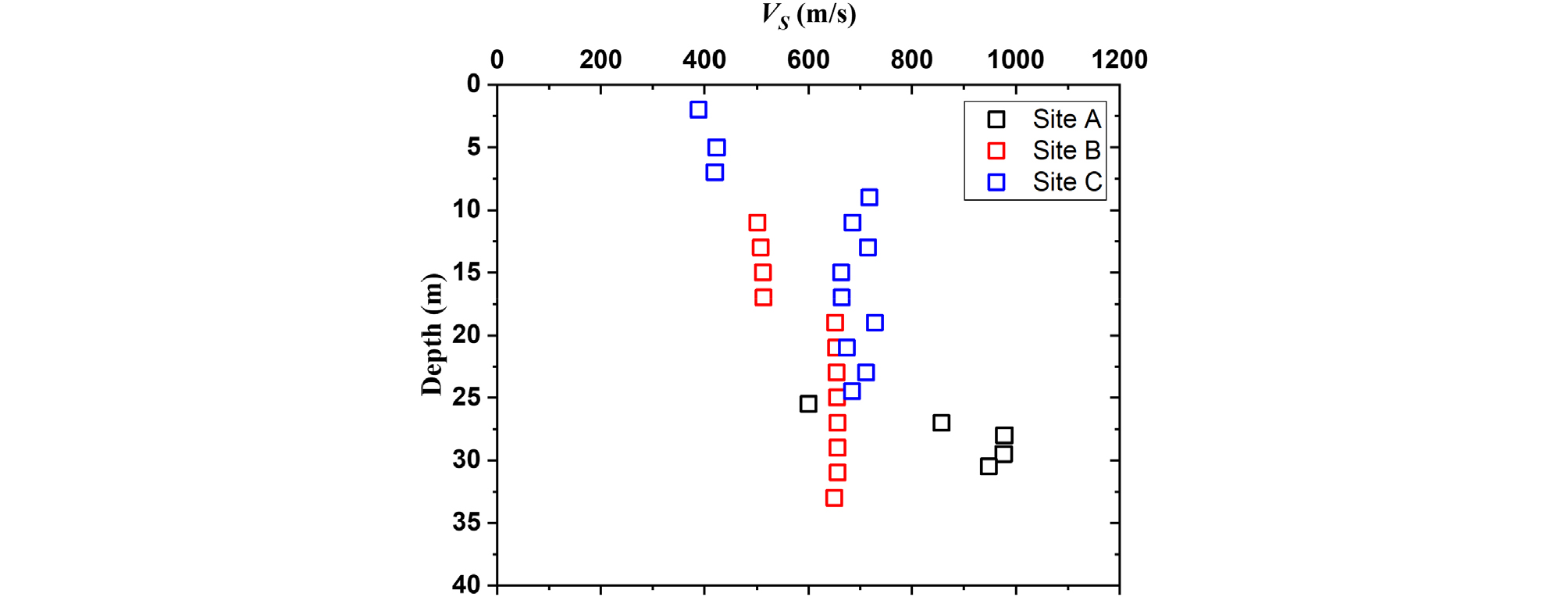
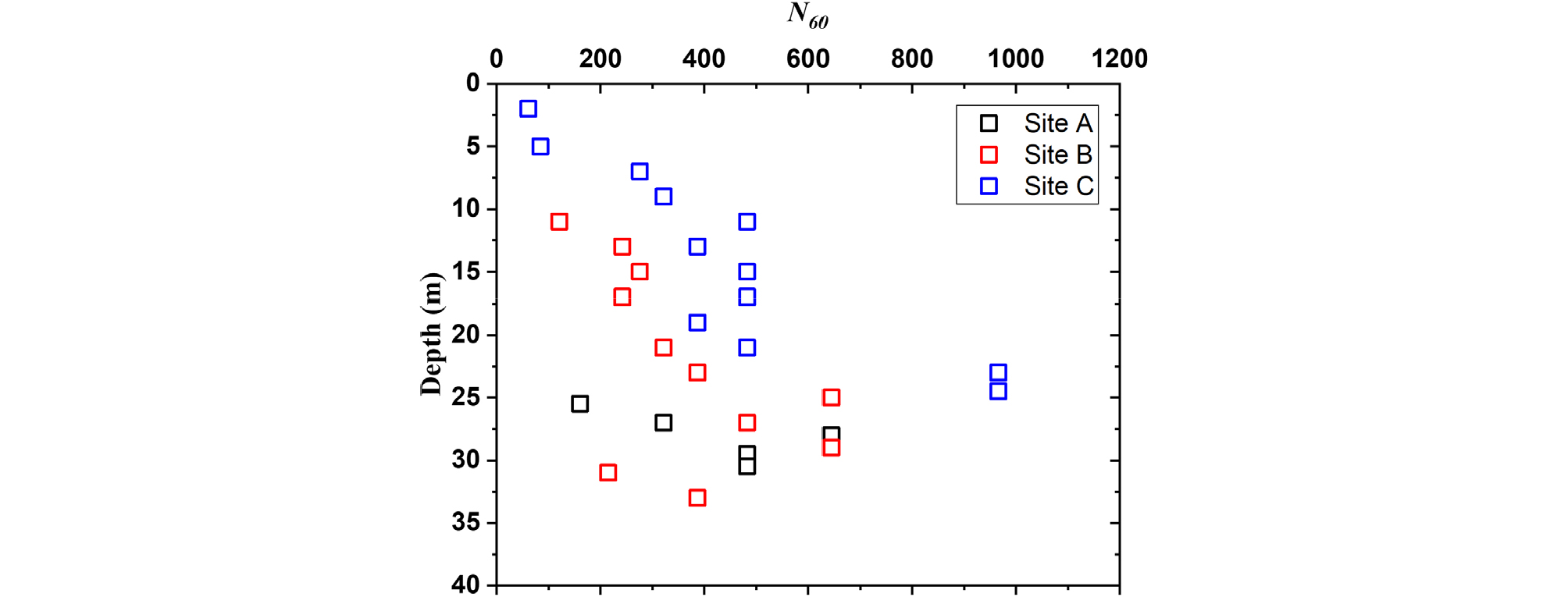
3개 현장에서 다운홀을 통해 측정한 전단파 속도는 약 389~987m/s의 범위로 나타나 국내 암반지층의 지진공학적 기반암을 결정하기 위해 풍화암의 전단파 속도를 분석한 Sun(2014)의 연구 결과(평균=665m/s, 표준편차=194m/s)와 유사하였으며, 전반적으로 심도가 깊어질수록 증가하는 것으로 나타났다(Fig. 3). 각 현장에서 측정한 전단파 속도는 풍화토와 풍화암의 경계(A 현장: 26m, B 현장: 17m, C 현장: 7m) 부근에서 뚜렷한 변화를 보였다. A 현장은 풍화토와 풍화암 경계에서 크게 증가하였으며, B 현장과 C 현장의 경우 현장 측정 N값을 바탕으로 결정한 풍화토와 풍화암 경계면보다 다소 깊은 심도에서 전단파 속도가 뚜렷하게 증가하였다. 3개 현장 모두 전단파 속도가 증가한 구간은 현장 측정 N값이 50타/6cm(선형 외삽하여 환산 시 N60=322)보다 큰 것으로 나타났다(Fig. 4). 국내 지반분류 기준 상 풍화토와 풍화암의 구분을 현장 측정 N값 50타/10cm로 정하고 있으나, 전단파 속도의 관점에서 분석 결과와 상이하므로 풍화암 분류 기준에 대한 추가적인 연구도 필요할 것으로 판단된다.
30cm 관입량으로 선형 외삽하여 환산한 N60은 3개 현장에서 61~966 범위로 나타났으며, 전반적으로 심도에 따라 증가하는 경향을 보였으나, 일부 구간에서는 감소하였다(Fig. 4). 선형 외삽한 N값과 30cm관입 시까지 타격하여 실측한 N값 관계에 대한 연구가 부족하지만, 국내 유사 연구에서 선형외삽한 N값을 적용하여 지반특성 분석에 활용하고 있고, 단순히 N값 50을 적용하는 것에 비해 합리적으로 지반특성을 평가할 수 있으므로, 정밀조사 위치 선정 등을 위한 예비조사에 충분히 활용 가능할 것으로 판단된다.
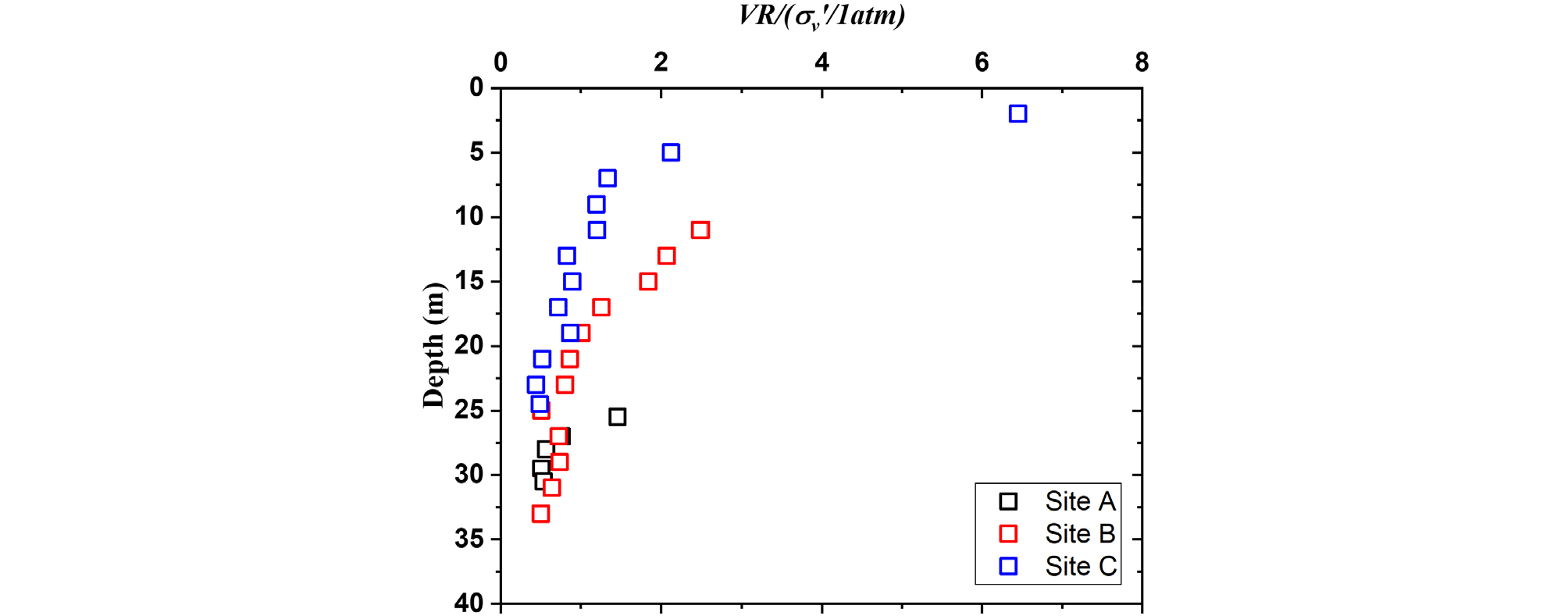
풍화는 신선암이 풍화되어 발생하는 지층이며 대상 현장 위치에 따른 지역적 특성 및 지질학적 특성에 의해 풍화대의 발생 심도가 다르게 나타난다. 3개 현장의 풍화대 발생 심도에 따라 풍화대에 작용하는 연직유효응력 차이가 발생하므로 이에 대한 영향을 배제하기 위해 본 연구에서는 연직유효응력과 대기압을 사용하여 VR을 정규화 하였다. 연직유효응력은 각 현장에서 수행된 밀도검층 자료를 활용하여 산정하였다. 정규화 한 VR은 심도가 증가함에 따라 전반적으로 감소하는 경향을 보였으며(Fig. 5), 이는 풍화가 진행됨에 따라 증가하는 VR의 이론적 경향 및 선행연구와 일치하였다(Arel and Tugrul, 2001; Price and Velbel, 2003; Ban et al., 2017). 본 연구에서는 N60, 정규화 한 VR을 사용하여, 전단파 속도를 추정하기 위해 비선형 다변량 회귀분석을 수행하였으며, 상세한 분석 방법 및 결과는 다음 절에 서술하였다.
4.2 비선형 다변량 회귀분석
3개 현장에서 측정한 N60과 채취된 시료의 XRF 분석을 통해 측정한 화학적 풍화지수(i.e. VR)를 활용하여 전단파 속도를 평가할 수 있는 추정식을 도출하기 위해 비선형 다변량 회귀분석을 수행하였다.
비선형 다변량 회귀분석에 앞서 전단파 속도와 N60 간의 단순회귀분석을 수행하여 기존 연구 결과와 비교하였다. 기존 국내 연구에서 제시한 풍화대의 전단파 속도와 N값의 상관관계는 거듭제곱 형태로 나타났으며, 결정계수는 0.165~0.342로 비교적 약한 상관관계를 보였다(Table 1). 특히, Sun et al.(2006)의 연구에서 제시한 상관관계의 결정계수가 타 연구자가 제시한 상관관계에 비해 비교적 크게 나타났으며, 이는 여러 암종의 풍화대에서 측정된 전단파 속도를 바탕으로 제시된 연구(Sun et al., 2008; Jung et al., 2009; Do et al., 2011)와 달리 모암이 동일한 특정 풍화대의 자료를 사용하여 분석하였기 때문으로 판단된다.
Table 1.
Empirical equations of VS in weathered granite with SPT-N in previous studies
| Empirical equations | Researchers |
| VS(m/s)=122.33(N)0.185 (R2=0.342) | Sun et al. (2006) |
| VS(m/s)=107.94(N)0.418 (R2=0.220) | Sun et al. (2008) |
| VS(m/s)=182.3(N)0.229 (R2=0.165) | Jung et al. (2009) |
| VS(m/s)=215.5(N)0.180 (R2=0.250) | Do et al. (2011) |
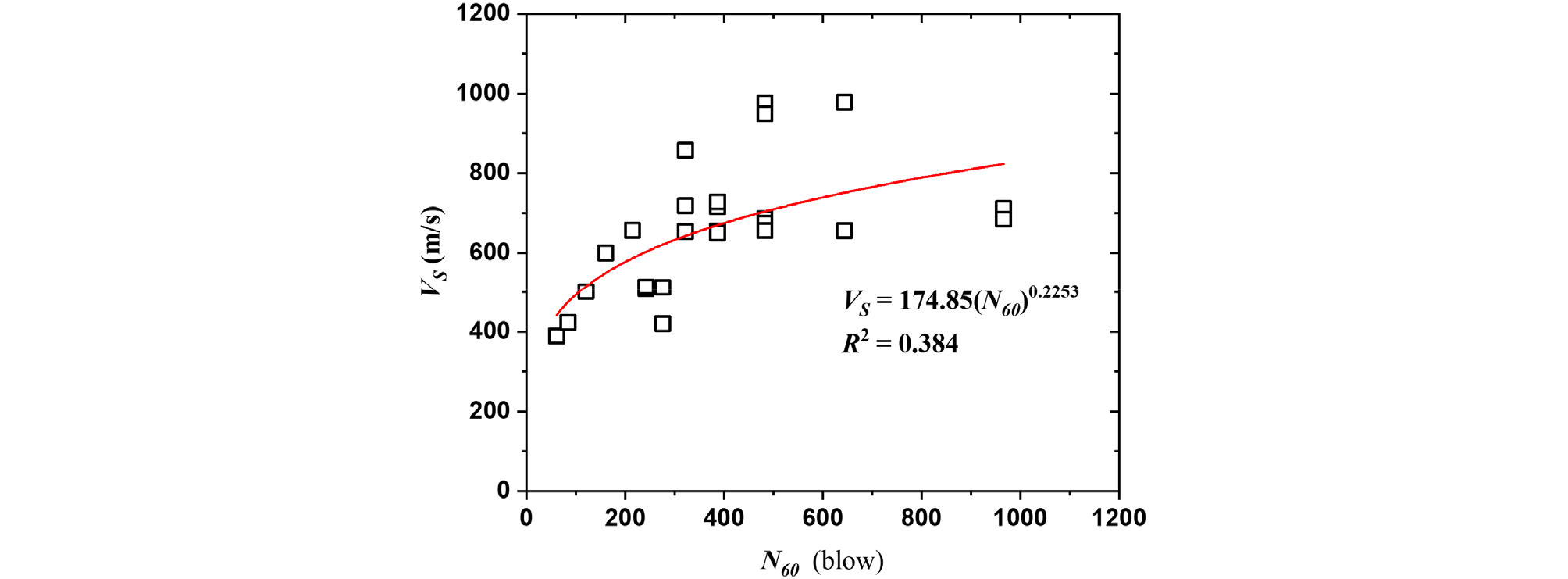
본 연구에서는 기존 연구를 참고하여, 화강 풍화대의 전단파 속도와 N60 관계를 식 (2)와 같이 설정하고 회귀분석을 수행하였다. 3개 현장의 전단파 속도는 전반적으로 N60에 따라 증가하였으나, 약 N60=322(현장 측정 N=50타/6cm) 이후부터 N60에 대응하는 전단파 속도의 편차가 증가하였다(Fig. 6). 이는 SPT 장비의 관입력 부족으로 비교적 단단한 풍화암에 대한 N60의 신뢰도가 감소하기 때문으로 판단된다. 3개 현장에서 측정한 전단파 속도와 N60을 바탕으로 분석한 화강 풍화대의 전단파 속도-N60 상관관계는 Jung et al.(2009)의 연구와 유사하게 나타났다(Fig. 6; Table 1). 결정계수는 0.384로 기존 연구들에 비해 좋은 상관성을 보였으나, 단단한 풍화암 지반에 대한 N60의 신뢰도 문제로 인하여 결정계수의 절대값은 비교적 약한 상관관계를 보였다.
본 연구에서는 기존 연구의 전단파 속도 추정식(Table 1)을 참고하여 독립변수인 N60과 정규화 한 VR을 거듭제곱 형태의 기본 함수로 설정하여 분석하였다(식 (3)). 다변량 회귀분석 시 독립변수들 간의 상관성은 회귀분석 결과의 신뢰도를 저하시킬 수 있으므로, 분산팽창지수를 확인하여 독립변수 간의 다중공선성(독립변수 간 상관성으로 인해 회귀분석 전체 가정을 위배하는 문제)을 확인하여야 한다. 통계학 이론에서는 다중공선성 검증을 위하여 분산팽창지수를 확인하며, 다중공선성에 문제가 없다고 판단되는 일반적인 기준은 분산팽창지수 10 미만이며, 엄격한 기준은 5 미만으로 제시하고 있다. 본 연구의 독립변수 간의 분산팽창지수는 1.5로 다변량 회귀분석의 독립변수로 적절함을 확인하였다.
비선형 다변량 회귀분석을 수행하여 도출한 전단파 속도와 N60 및 정규화 한 VR의 관계식은 식 (4)와 같다. 도출한 관계식의 결정계수는 0.528로 기존 연구자들이 제시한 전단파 속도-N60 관계(Table 1)에 비해 좋은 상관도 보이는 것으로 나타났다. 또한, 본 연구에서 도출한 전단파 속도 추정식의 정확도를 확인하기 위해 최소제곱근오차(RMSE: Root mean square error)를 산정한 결과 기존 제안식에 비하여 정확도가 향상된 것을 확인하였다(Table 2). 이는 기존 연구자들이 제안한 전단파 속도 추정식은 N60만을 변수로 사용하여 분석하였기 때문에 특정한 N60에서 하나의 전단파 속도를 추정하지만 본 연구에서는 풍화도를 평가할 수 있는 풍화지수(i.e. VR)를 추가하여 동일한 N60 에서도 풍화도에 따라 보다 세밀하게 전단파 속도를 추정할 수 있기 때문으로 판단된다. 결정계수의 절대적인 수치(0.528)는 강한 상관도를 나타내지 않았지만 기존 연구의 결정계수를 고려하였을 때, N60만을 사용한 단순 회귀분석에 비해 풍화지수를 추가 변수로 사용하여 결정계수가 증가한 것에 의미가 있다.
Table 2.
RMSE (Root mean square error) of each empirical equation
| Researchers | RMSE |
| Sun et al. (2006) | 321 |
| Sun et al. (2008) | 130 |
| Jung et al. (2009) | 123 |
| Do et al. (2011) | 123 |
| This study | 101 |
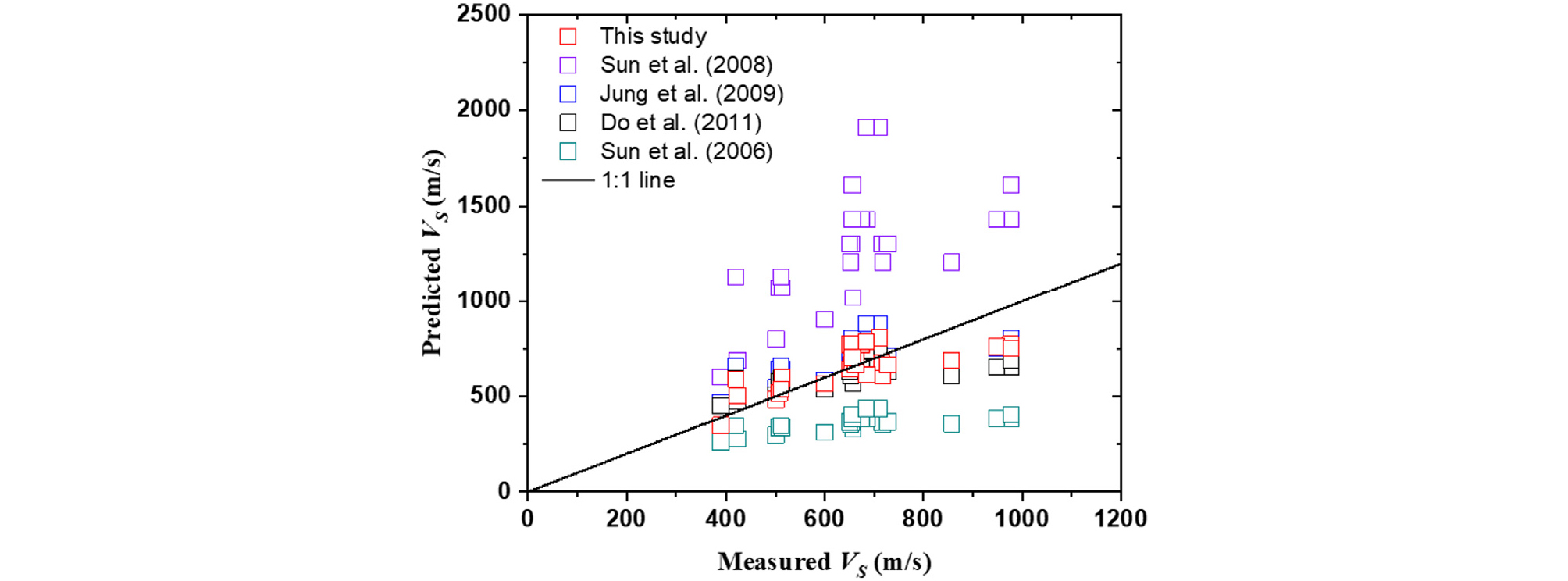
기존 제안식(Table 1)을 이용하여 추정한 전단파 속도와 비교한 결과(Fig. 7), 본 연구의 전단파 속도 추정식은 Jung et al.(2009) 및 Do et al.(2011)의 연구결과와 유사한 범위를 갖는 것으로 나타났다. 반면, Sun et al.(2008)의 연구결과는 전단파 속도를 과대 평가하였고, Sun et al.(2006)의 제안식은 과소 평가하였다. 본 연구에서 사용한 데이터를 활용하여 각 연구에서 전단파 속도와 N값의 상관관계를 평가하기 위해 사용된 데이터 수가 제한적이고 지역적 차이 등으로 인해 추정식의 편차가 발생한 것으로 판단된다. 향후, 풍화특성을 대변할 수 있는 화학적 풍화지수와 전단파 속도 데이터를 충분히 확보하여 추가적인 분석이 이루어질 경우 지반조사 시 국내 화강 풍화대의 특성을 평가할 수 있는 방법으로 활용할 수 있을 것으로 판단된다.
5. 결 론
본 연구에서는 표준관입시험을 통해 측정한 N60과 풍화도를 정량적으로 평가할 수 있는 화학적 풍화지수를 사용하여 전단파 속도를 추정할 수 있는 경험식을 제시하였다. 국내 3개 현장에서 수집된 화강 풍화대의 N60, 전단파 속도, VR을 사용하였으며, N60과 정규화한 VR을 독립변수로 하는 비선형 다변량 회귀분석을 수행하여 전단파 속도 추정식을 제안하였고, 국내 풍화대를 대상으로 수행된 선행 연구 결과와 비교하였다. 본 연구를 통해 발견한 사실과 결론은 다음과 같다.
(1) 각 현장에서 측정한 전단파 속도는 풍화토와 풍화암의 경계 부근에서 뚜렷한 변화를 보였다. 특히, B 현장과 C 현장의 경우 현장 측정 N값을 바탕으로 결정한 풍화토와 풍화암 경계면 보다 다소 깊은 심도에서 전단파 속도가 뚜렷하게 증가하였다. 3개 현장 모두 전단파 속도가 증가한 구간은 현장 측정 N값이 50타/6cm(본연구의 N60=322)보다 큰 것으로 나타났다. 국내 지반분류 기준 상 풍화토와 풍화암의 구분을 현장 측정 N값 50타/10cm로 정하고 있으나, 전단파 속도의 관점에서 분석 결과와 상이하므로 풍화암 분류 기준에 대한 추가적인 연구도 필요할 것으로 판단된다.
(2) 3개 현장의 전단파 속도는 전반적으로 N60에 따라 증가하였으나, 약 N60=322(현장 측정 N=50타/6cm) 이후부터 N60에 대응하는 전단파 속도의 편차가 증가하였다. 이는 SPT 장비의 관입력 부족으로 비교적 단단한 풍화암에 대한 N60의 신뢰도가 감소하기 때문으로 판단된다. 3개 현장에서 측정한 전단파 속도와 N60을 바탕으로 분석한 화강 풍화대의 전단파 속도와 N60 상관관계는 Jung et al.(2009)의 연구와 유사하게 나타났으며, 결정계수는 0.384로 기존 연구들에 비해 좋은 상관성을 보였으나, 단단한 풍화암 지반에 대한 N60의 신뢰도 문제로 인하여 결정계수의 절대값은 비교적 약한 상관관계를 보였다.
(3) 비선형 다변량 회귀분석을 수행하여 도출한 전단파 속도와 N60 및 정규화 한 VR의 상관관계에 대한 결정계수는 0.528로 나타나 기존 연구자들이 제시한 전단파 속도-N60 관계에 비해 증가하였으며, 본 연구에서 수행한 전단파 속도-N60의 결정계수(0.384)에 비해 약 0.15 증가하였다. 결정계수의 절대적인 수치(0.528)는 강한 상관도를 나타내지는 않았지만 기존 연구의 결정계수를 고려하였을 때, N60만을 사용한 단순 회귀분석에 비해 풍화지수를 추가 변수로 사용하여 결정계수가 증가한 것에 의미가 있다.
(4) 기존에 연구자들이 제안한 전단파 속도 추정식은 N60만을 변수로 사용하여 분석하였기 때문에 특정한 N60에서 하나의 전단파 속도를 추정하지만 본 연구에서는 풍화도를 평가할 수 있는 풍화지수(i.e. VR)를 추가하여 특정한 N60 에서도 풍화도에 따라 다수의 전단파 속도를 추정할 수 있다. 이는 동일한 N60을 갖는 풍화대에서 풍화도에 따라 보다 세밀하게 전단파 속도를 추정할 수 있음을 의미하므로, 현장의 풍화특성을 반영하여 보다 정확하게 전단파 속도를 평가할 수 있을 것으로 판단된다.
향후, 화강 풍화대의 전단파 속도와 화학적 풍화지수 데이터를 확보하여 추가적인 분석이 이루어질 경우 본 연구에서 제안한 전단파 속도 추정식을 보완하여 지반조사 시 화강 풍화대의 특성을 평가할 수 있는 방법으로 활용할 수 있을 것으로 판단된다. 데이터 수집 이외에 풍화암의 전단파 속도 평가의 신뢰성을 보다 향상시키기 위해서는 N값 50 이상의 단단한 풍화암에 대한 선형외삽이 아닌 적합한 환산방법에 대한 연구가 진행되어야 할 것으로 판단된다. 또한, 국내 풍화암 분류기준인 N=50타/10cm 보다 단단한 풍화암(N=50타/6cm)에서 전단파 속도의 뚜렷한 증가가 발견되었으므로, 국내 지반조사 자료를 바탕으로 풍화대의 지반정수와 N값의 분포를 분석하여 공학적 의미의 풍화암 분류 기준에 대한 연구도 필요한 것으로 판단된다.