1. 서 론
2. 말뚝재하시험
2.1 현장 개요 및 시험 계획
2.2 지반조건
3. 시험결과 분석
3.1 항타 응력
3.2 동재하시험(시항타)
3.3 동재하시험(재항타)
3.4 정재하시험
4. 동역학적 지지력 공식을 이용한 항타시공관리
5. 결 론
1. 서 론
항타 말뚝공법은 기성 말뚝을 해머(또는 항타기)로 타격하여 말뚝을 지중에 설치하는 공법으로, 빠른 시공속도로 경제적일 뿐 아니라, 지지층에 관입 시키기 위한 타격에너지와 말뚝의 관입량의 관계로부터 시공 중 말뚝 지지력을 간접적으로 확인하며 시공할 수 있는 장점이 있다. 국내의 경우 도심지 건설에서 소음 및 진동 등의 사회, 환경 문제로 매입공법 적용이 증가하고 항타 말뚝공법의 사용빈도가 감소하고 있으나, 시공 편의성 및 경제성 때문에 주거지와 떨어진 연안의 항만공사나 대규모 토목사업에서 여전히 제한적으로 사용되고 있다. 그러나 베트남을 비롯한 여러 동남아 국가에서는 항타공법은 가장 널리 쓰이는 말뚝 공법으로 유압 해머 뿐 아니라 국내에서는 환경문제 및 민원 등으로 사용을 지양하고 있는 디젤 해머도 많이 쓰이고 있는 상황이다.
항타말뚝의 지지력 연구의 초기에는 에너지 보존법칙을 토대로 제안된 항타공식(또는 동역학적 지지력 공식, dynamic formula)을 중심으로 연구가 이루어졌다. 항타공식에서의 항타에너지는 말뚝 관입시 지반 저항력과 항타시 발생한 에너지 손실의 합으로 나타낼 수 있는데, 이는 사용성이 간편한 장점이 있으나 에너지 손실과 경험계수 산정, 항타 중 측정되는 값들의 정확도에 따라 그 신뢰성이 크게 달라지는 문제가 있다(FHWA, 2016; Chung and Kim, 1985). 또한 항타공식은 긴 말뚝을 하나의 집중된 질량(lumped mass)으로 기본 전제하기 때문에 말뚝 내에 작용하는 응력을 고려하지 않는 기본적인 문제가 내제되어 있다. 이후 이를 보완하기 위해 말뚝을 여러 질량계의 합으로 가정하여 일차원 파동방정식(one-dimensional wave equation)으로 풀이한 동적해석 방법이 제안되었고, 이는 말뚝의 극한 지지력과 항타응력의 예측할 수 있을 뿐 아니라 항타장비 조합에 따른 항타시공성(drivability)도 함께 평가할 수 있는 장점을 가지고 있다(Pile dynamics inc, 2015). 그러나 일차원 파동방정식은 말뚝내의 응력 변화로부터 말뚝의 변위와 시간 그리고 요소위치 사이의 관계를 결정하기 위해서는 항타공식에 비해 상대적으로 많은 초기조건과 경계조건을 필요로 하기 때문에, 현장 시공관리단계에서는 입력 값 산정의 불확실성 등으로 적용에 용이치 않은 문제가 있다(Hong et al., 1997; Randolph, 2003; Masouleh and Fakharian, 2008).
이러한 불확실성으로 인해 어느 일정 규모 이상의 말뚝 시공 현장에서는 동재하시험 또는 정재하시험을 수행하여 설계 지지력이나 극한 지지력을 확인하고 있으며, 특히 동재하시험은 정재하시험과 비교하여 상대적으로 소요 시간이 적게 들고 경제적이며 시험시 말뚝의 시공품질 또한 평가할 수 있어 널리 적용되고 있다(Seo et al., 2015; La et al., 2011). 그러나 말뚝의 시공관리에 있어서는 동재하시험이나 정재하시험의 횟수 등 제한된 관리 규정만 있으며, 전체 말뚝에 대한 시공관리방법은 명확하게 규정되어 있는 가이드라인이 있지 않다. 또한 현실적으로 수많은 말뚝을 시공하는데 품질관리를 위하여 모든 말뚝에 대하여 재하시험을 실시할 수도 없기 때문에 일반적으로 국내외의 기성 말뚝 시공현장에서는 전체 물량의 1~10%의 말뚝에 대해 동재하시험을 수행하여 지지력을 확인하고, 나머지 말뚝은 시공직후의 최종 관입량을 측정하여 관리 기준 값과 비교 후 적정성을 판단하고 있다(AASHTO 2010; ICC, 2002; Standards Australia, 2009; KGS, 2018). 따라서 항타 관리 기준 값 산정방안이 전체 말뚝시공관리에 있어서 매우 중요하다 할 수 있다.
이에 본고에서는 베트남 중부 연안의 대심도 점토지반을 대상으로 항타 시공된 마찰 강관 말뚝의 동재하시험과 정재하시험의 결과를 토대로 항타 관입성과 지지력 특성을 비교 분석하고, 수정된 항타공식을 활용한 현장 항타 시공관리 방법에 대해 고찰하였다.
2. 말뚝재하시험
2.1 현장 개요 및 시험 계획
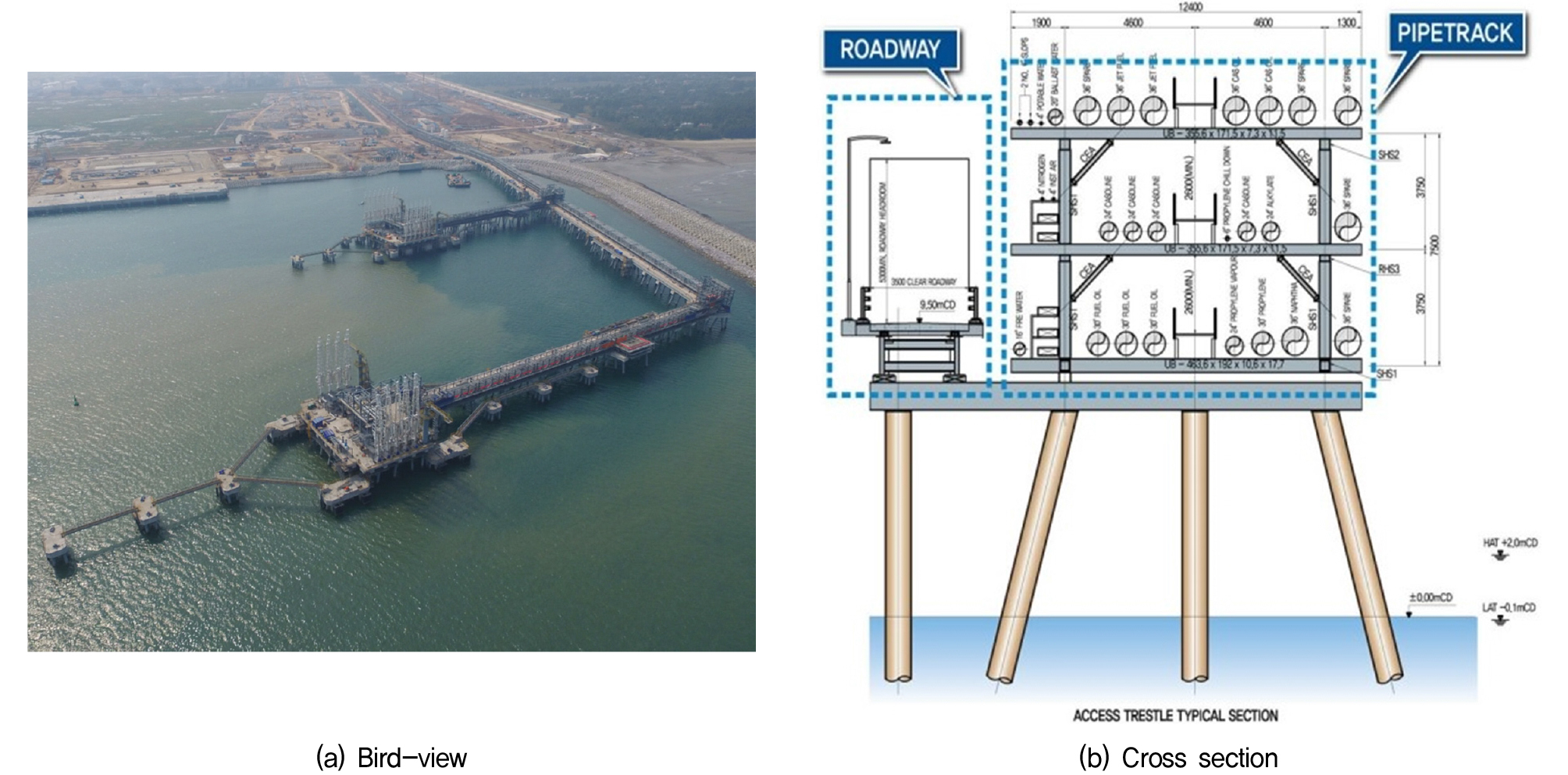
본 연구에서 시공된 시험말뚝(Test Pile)은 베트남 중부 연안에 위치한 00 정유석유화학플랜트를 위한 항만·해안공사 중 부두시설(Jetty)과 약 900m 연장의 해상교량(Trestle)의 기초시공을 위해 수행되었다. Jetty는 유류운송 목적 선박을 위한 항만시설로서, 출하 장비(Loading Arm)가 설치되는 메인 로딩 플랫폼(Loading Platform)과 접안 돌핀(Breasting Dolphin) 및 계류 돌핀(Mooring Dolphin)으로 구성되었고. Trestle에는 유류 운송을 위한 파이프 랙(Pipe rack)과 Jetty에 차량 이 접근할 수 있도록 도로(Roadway)가 계획되었다(Fig. 1 참조).
Jetty와 Trestle의 본 말뚝기초는 직경 914mm 및 812mm 두 종류의 강관말뚝을 항타 시공으로 계획되었다. 앞서 기술한 바와 같이 국내 항타말뚝 시공의 경우 풍화암 또는 기반암까지 항타하여 선단지지하는 것이 일반적이나, 본 현장의 대상 지반은 5m 두께 전후의 모래층 아래에 단단한(firm to stiff) 점토층이 두텁게 분포하고 있으며 기반암은 약 G.L-79~104m 사이에 존재함에 따라 경제성과 시공성을 고려하여 마찰말뚝으로 계획되었다.
본 현장의 말뚝재하시험은 시험말뚝의 주면 마찰 지지력 및 항타 시공성을 확인하여 본 시공시 항타 관리기준을 수립하기 위해 계획되었다. 이에 총 5본의 시험말뚝을 대상으로 정재하 및 동재하시험이 본 말뚝기초 시공 전에 사전 시행되었다. 시험 말뚝은 본 말뚝과 동일하게 두 종류(Φ914x18, Φ812x16)로 이루어졌으며, 유압해머(DKH1516)와 디젤해머(DELMAG D100-13)의 시공성 및 항타 시공관리기준을 수립하기 위해 해머별로 복수로 시공하여 ASTM D4945-17(2013)에 따라 시항타(End of initial strike, EOID) 동재하시험을 수행하였다(Table 1 참조). 점토층에 지지된 마찰말뚝의 경우 시간경과에 따른 지지력 증가(set-up) 효과가 예상됨에 따라 시험말뚝 시공 후 2주 간격을 두어 재항타(restrike) 동재하시험 및 정재하시험(static load test. SLT)을 각각 수행하였다. 본 현장의 동재하시험시 시항타 및 재항타에 적용된 해머 제원은 Table 2와 같다.
Table 1.
Summary of pile load test
Table 2.
Specification of pile hammer
2.2 지반조건
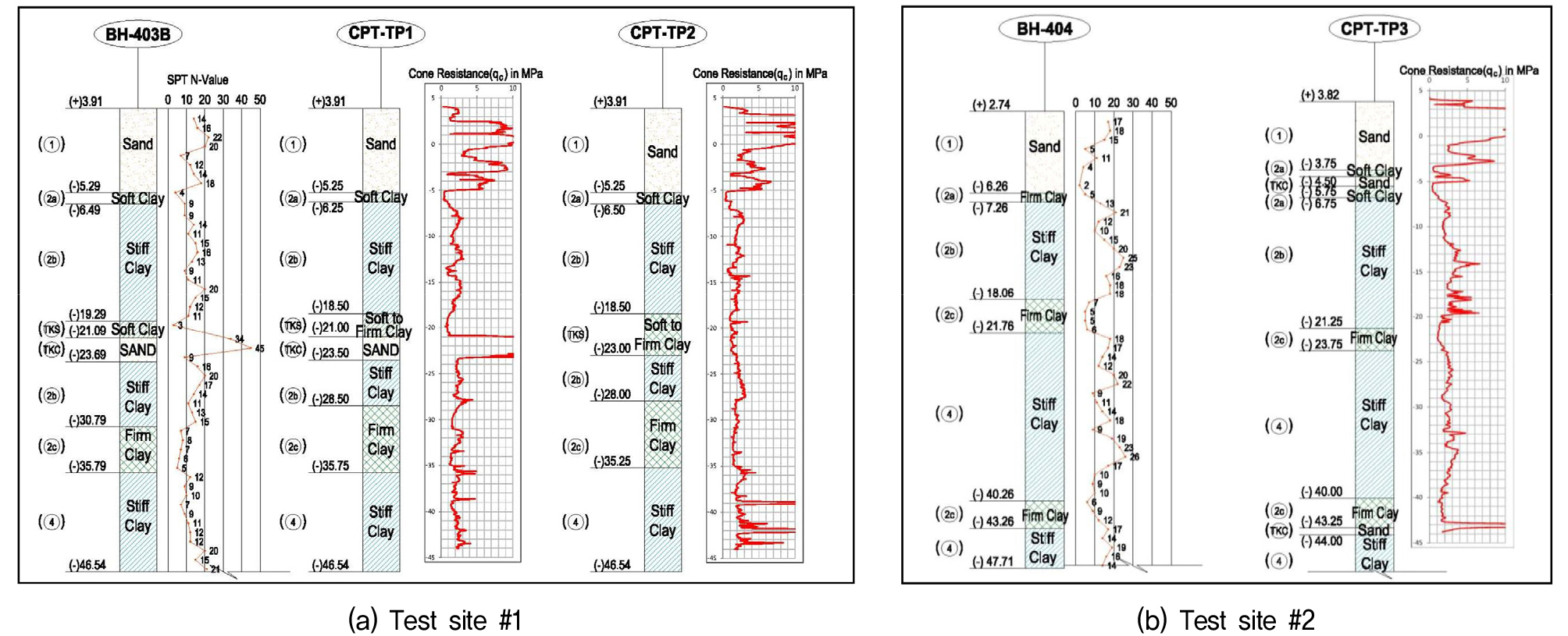
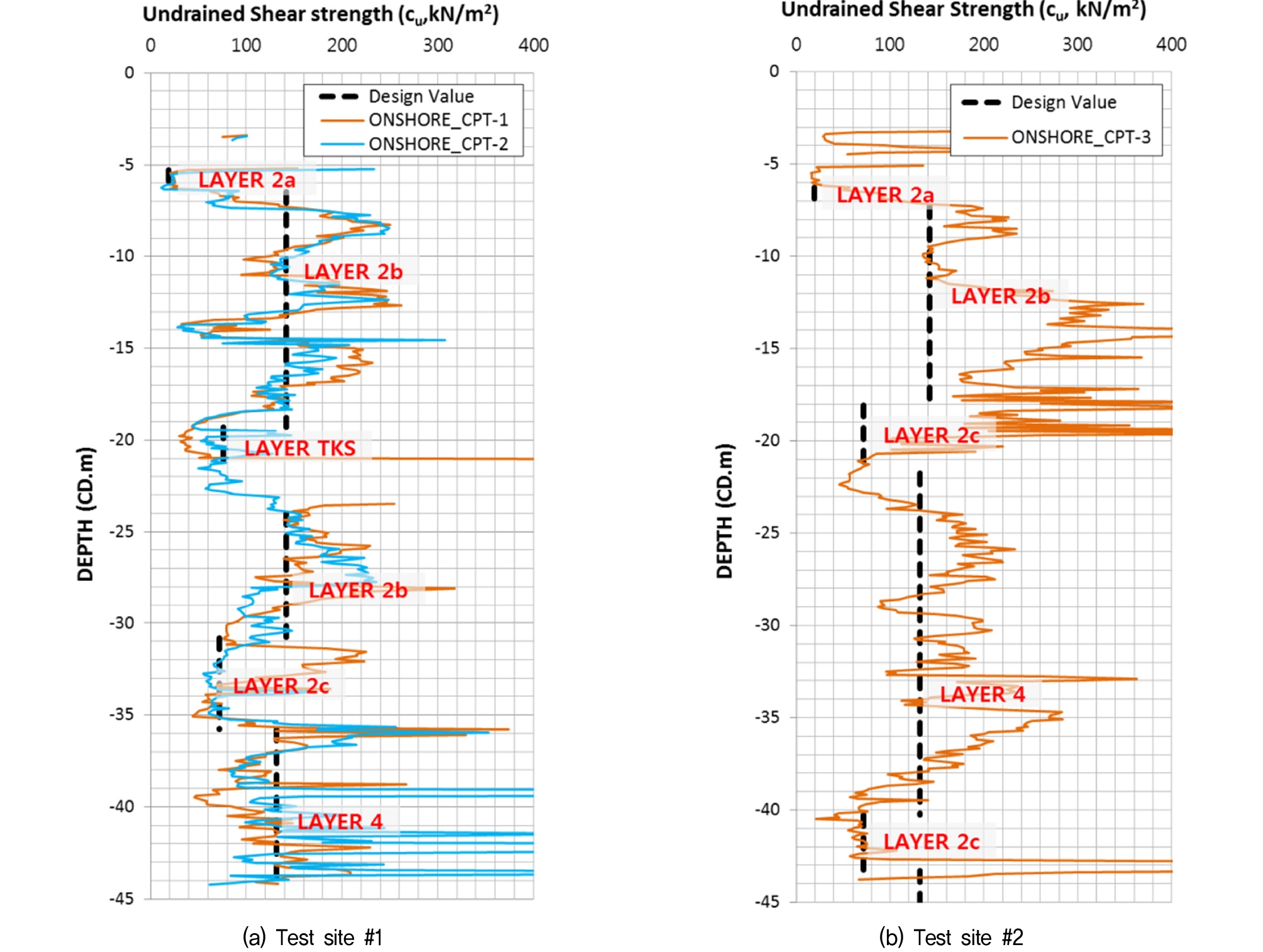
시험말뚝이 시공된 지층조건은 Fig. 2와 같이, 상부 4~6m 두께의 모래층 아래에 단단한(firm to stiff) 점토층이 주를 이루고 있으며, 두께 1~2m 정도의 점토질 또는 실트질 모래가 일부 렌즈형태로 점토층 사이에 분포하는 것으로 나타났다. 시험부지내 점토층의 경우 심도에 따라 Fig. 2와 같이 값이 증가하지 않고 조사심도(GL-48m)까지 대체로 일정한 범위를 나타났다. Table 3은 지층 별 설계물성을 요약한 것으로 시험부지를 포함한 현장 전체의 지반조사 결과를 토대로 산정된 결과이며, Fig. 3은 지층의 설계물성과 시험부지에서 수행된 콘관입시험(CPTu) 결과로부터 추정한 비배수 전단강도 값을 심도별로 비교하여 나타낸 것으로, 설계 지반물성이 점토질 지반의 강도특성을 잘 대변하는 것으로 나타났다. CPTu 결과를 이용한 비배수 전단강도 추정식은 다음 식 (1)과 같다(Lunne et al., 1997).
Table 3.
Summary of soil properties
여기서, qt는 보정된 콘관입저항치, σvo는 해당위치의 상재 응력, NKt는 피에조콘 계수로서 실시설계시 사용된 11.1을 동일하게 적용하였다.
3. 시험결과 분석
3.1 항타 응력
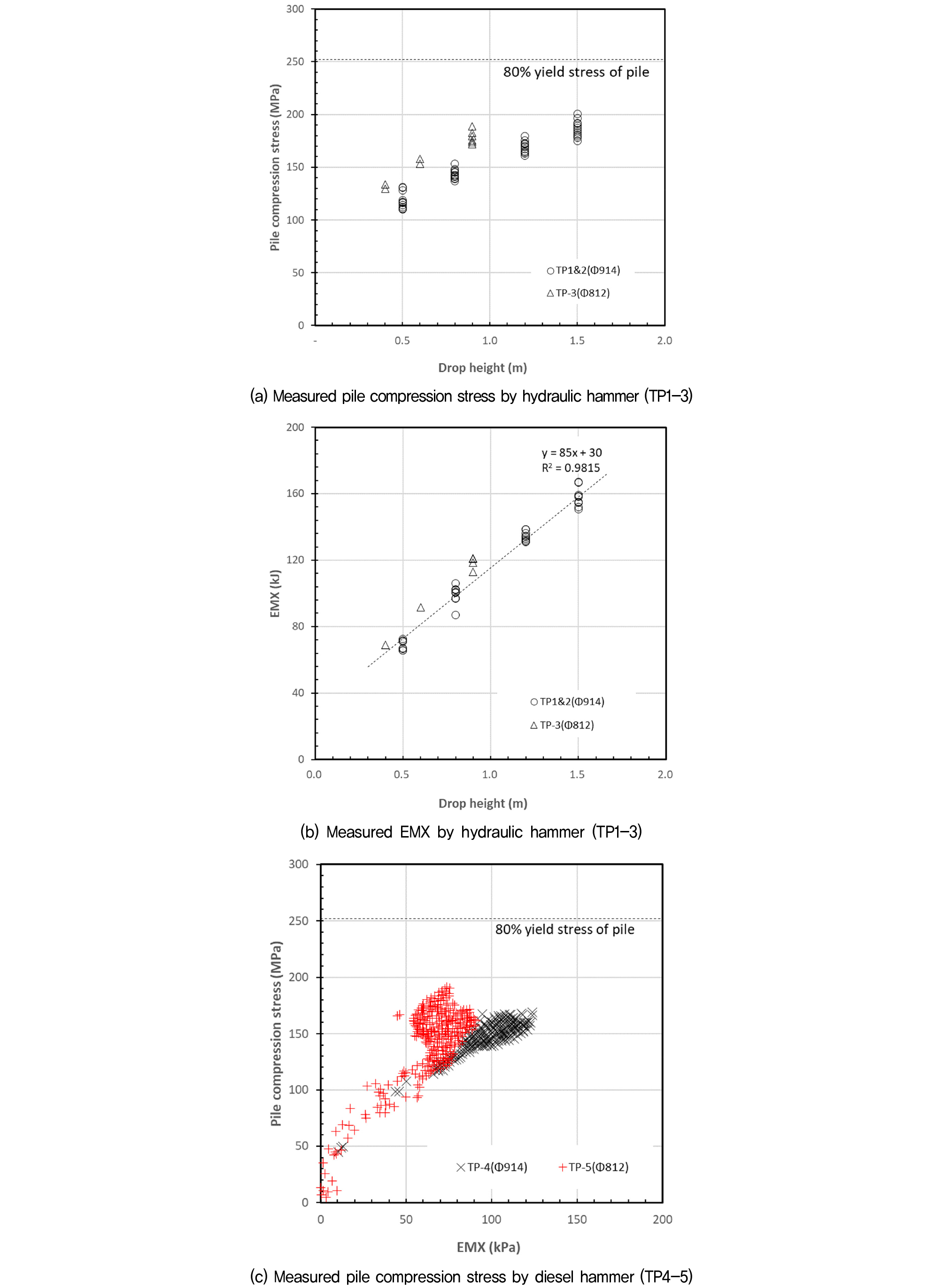
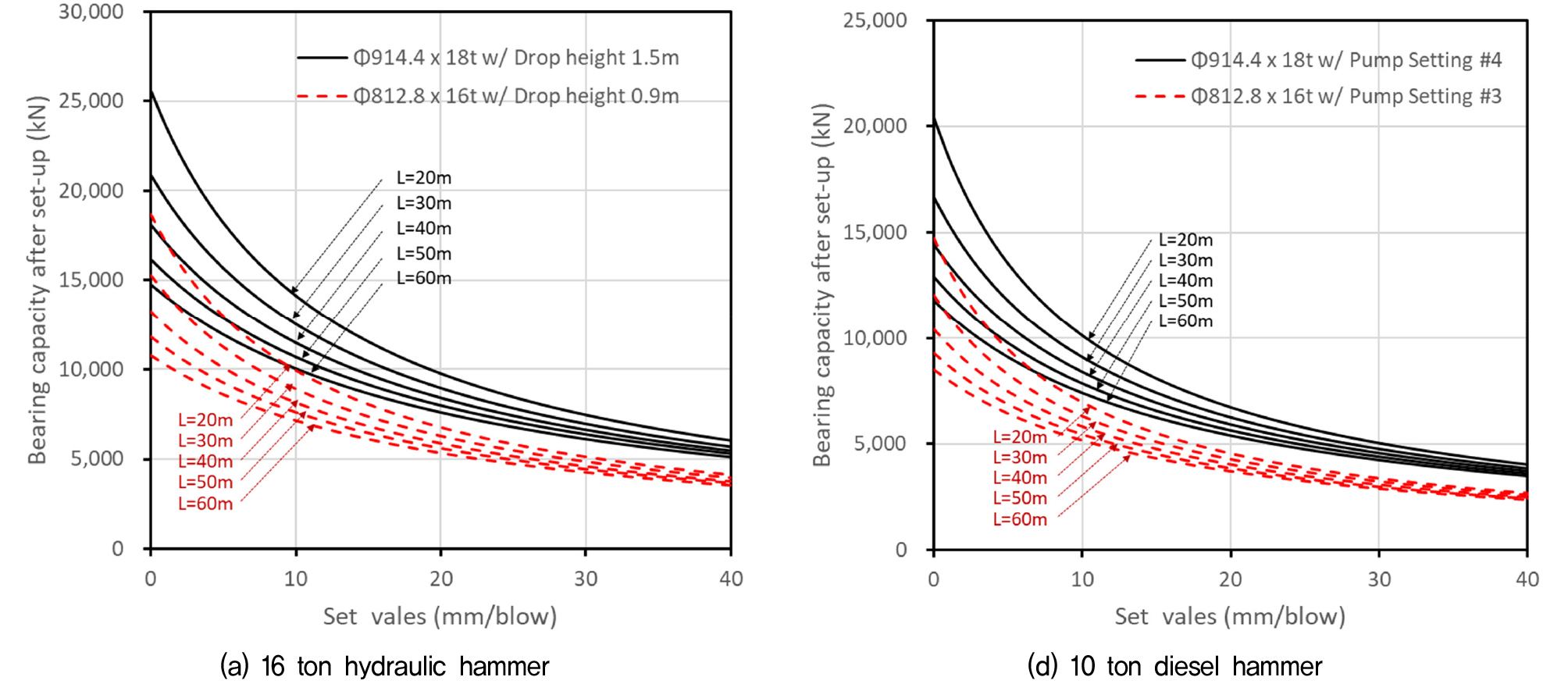
강관말뚝 항타시, 허용 항타응력은 일반적으로 강관의 항복강도의 80%를 적용하여 그 이하로 관리한다(FHWA, 2006; ASCE, 2016). 본 시험말뚝 재료의 항복강도는 315 MPa로 허용 항타응력은 80%인 252MPa로 관리되었으며, Fig. 4(a)와 같이 유압해머(램 중량 16ton)로 시공된 시험말뚝 TP1~3은 응력 측정결과 이를 만족하는 것으로 나타났다. 이때 시험말뚝 TP3(Φ812x16t)의 경우 단면적이 TP1~2(Φ914x18t)보다 상대적으로 작기 때문에 램 낙하고를 0.4~0.9m이내로 줄여 허용 항타응력 이내로 항타 시공하였다.
본 현장에서 사용된 유압해머 DKH-1516의 경우 Fig. 4(a), (b)와 같이 해머의 램 낙하고(h=0.4~1.5m)가 높아짐에 따라 PDA로 측정된 말뚝의 압축응력과 말뚝에 두부에 전달된 최대 항타 에너지(EMX, maximum energy transferred to pile) 값이 선형적으로 비례 증가하며 일정한 추세를 보인다. 이로부터 유압해머 DKH-1516의 램 낙하고와 EMX값 관계를 회귀 분석하면 다음과 같다.
따라서, 유압해머 DKH-1516의 효율, e(driving efficiency)는 다음과 같이 해머의 램 낙하고의 함수로 나타낼 수 있다.
여기서, 해머의 energy input은 해머의 램 중량(w=16ton), 램 낙하고(h), 중력가속도(g)의 곱이다. 기존 문헌(Kim et al., 2000; Seo et al., 2015)에 따르면 일반적인 유압해머의 효율은 90%정도로 알려졌으며, 실무에서는 실제 효율을 측정하지 않은 경우 이를 일괄적으로 준용하는 실정이다. 그러나 본 시험에서는 램 낙하고(h)가 증가함에 따라 유압해머의 효율이 상기 식 (3)과 같이 감소하는 것으로 나타났다.
DELMAG D100-13 디젤해머의 경우, 램 낙하고가 아닌 에너지 출력을 조절하는 펌프 셋팅(pump setting)에 따라 항타 에너지를 조절하는데, 본 시험에서는 Fig. 4(c)와 같이 시험말뚝 TP4~5 모두 hammer specification에 제안된 최대 항타 에너지(333kJ) 대비하여 항타 효율이 낮게 나타났으며, 말뚝에 발생하는 응력의 변동성이 유압해머에 비해 상대적으로 크게 나타났다. TP5의 경우 EMX와 말뚝 응력이 일정한 선형관계를 보이나, TP4의 경우 일정한 추세를 보이지 않는 것으로 보아 항타시공 중 편타 또는 계측 오차가 있는 것으로 추정된다. 따라서 일정한 추세를 보이는 TP5 기준으로 보았을 때 디젤해머 해머효율은 25~35%(평균30%) 정도로 확인되며, 편타 등이 발생했을 때 TP4와 같이 효율이 15%이하까지도 낮아질 수 있음을 알 수 있었다.
3.2 동재하시험(시항타)
시항타 동재하시험(End of initial driving, EOID)은 시험말뚝 5본을 대상으로 모두 수행되었으며, 앞서 기술한 바와 같이 본 시공시 해머에 따른 영향을 고려하기 위해 시험말뚝 TP1~3은 16ton 유압해머, 시험말뚝 TP4~5는 10ton 디젤해머를 이용하여 시험을 진행하였다.
EOID 극한 지지력은 CAPWAP(CAse Pile Wave Analysis Program)방법을 통해 산정하였으며, 그 결과는 Table 4와 같다. 시험부지#1에서 수행된 TP1, TP2, TP4(Φ914x48)의 측정된 주면마찰력은 2,040~2117kN으로 유사하게 나타났으며, 시험부지 #2에서 수행된 TP3, TP5(Φ812x47)의 주면마찰력은 2,697~2,894kN 범위로 해머타입에 따른 주면마찰력 차이는 나타나지 않았다. 다만 직경이 작은 TP3과 TP5(Φ812x47)의 주면마찰력이 Φ914 시험말뚝보다 크게 나온 것은 본 시험부지#1과 #2의 지반조건이 크게 다르지 않는 것을 감안하였을 때, 항타 관입시 지반교란 측면에서 소구경이 상대적으로 유리하였으리라 추정된다.
Table 4.
Results of EOID
선단지지력의 경우, 디젤해머를 이용하여 동재하시험을 수행한 TP3과 TP5는 620~622kN으로 나타나 유압해머를 이용한 TP1,2,4의 선단지지력(172~273kN)보다 다소 크게 나타났는데, 이는 유압해머 사용시의 EMX가 디젤해머 사용시보다 큰 것을 감안하였을 때 설명하기 어려운 사항이다. 다만 본 재하시험의 경우 선단지지력 비중이 전체 말뚝 지지력에 비해 상대적으로 낮기 때문에 EOID를 통해 주면/선단 지지력을 구분함에 있어 불확실성이 있었으리라 판단된다.
EOID을 통해 측정된 전체 지지력은 약 2,285~3,359kN으로 본 시험말뚝의 설계지지력(Table 1 참조)에 미치지 못하였다. 동재하시험시 말뚝지지력은 동하중 재하시의 저항력이 아니라 항타시 발휘된 저항력(mobilized resistance)를 의미하는 것으로 이는 정적 말뚝지지력과 차이가 발생될 수 있다. 이러한 차이는 첫째, 동재하시험시 램 중량이 작아 흙의 지지력을 발휘 시킬 수 있는 충분한 항타에너지가 가해지지 않았을 경우 지지력을 과소평가될 수 있다. 이는 통상 항타시 말뚝 관입량이 2.5mm/blow 이하일때로, 본 EOID시 final set value는 6.9~38mm 범위로 측정되었으므로 EOID시 항타에너지는 충분했던 것으로 판단된다. 둘째로는 시간 경과에 따른 말뚝 지지력의 증가(set-up) 영향으로 차이가 발생될 수 있는데, 말뚝 항타시 발생한 주변 흙의 교란과 과잉간극수압이 시간이 지나면서 안정화되어 말뚝 지지력이 증가하는 현상을 의미한다. 이러한 말뚝의 set-up 효과는 본 현장과 같이 주로 점성토지반에서 발생된다(Randolph et al., 1979; Pestana et al., 2002; Jensen, 2004). 이에 대한 논의는 다음절에서 다루었다.
3.3 동재하시험(재항타)
본 현장시험에서 시간경과에 따른 장기 지지력 증가비(set up factor, SUF) 산정을 위하여 EOID 시험 2주후에 재항타(restrike) 동재하시험을 수행하였으며, CAPWAP을 이용한 지지력 산정 결과는 다음 Table 5와 같다. 충분한 항타에너지를 가하기 위하여 40ton 램 중량을 가진 드롭 해머(drop hammer)를 이용하였으며, 허용 항타응력을 감안하여 낙하고는 1.0~1.5m 범위로 적용하였다. restrike를 통한 측정된 극한 지지력은 EOID에 비해 3~6배 증가한 것으로 나타났다. 대부분의 지지력은 주면에서 발현하였으며, 선단지지력은 전체 지지력의 10%내외에 불과하였으며 EOID시 측정된 선단지지력보다 낮게 나타났다. 본 시험의 경우 측정된 set-value 값이 17.5~37mm 범위로 나타난 바와 같이 40ton의 램 중량의 드롭 해머를 이용하여 선단의 극한 지지력이 충분히 발현시킬 항타에너지를 가한 것으로 판단된다. 그럼에도 불구하고 EOID시 측정된 선단지지력보다 낮은 것은 항타에너지 부족 보다는 동재하시험을 통해 주면/선단 지지력을 구분함에 있어 불확실성이 있음을 보여준다 판단된다. 이는 다음 정재하시험 결과에 대한 부분에서 추가적으로 기술하였다.
Table 5.
Results of restrike
3.4 정재하시험
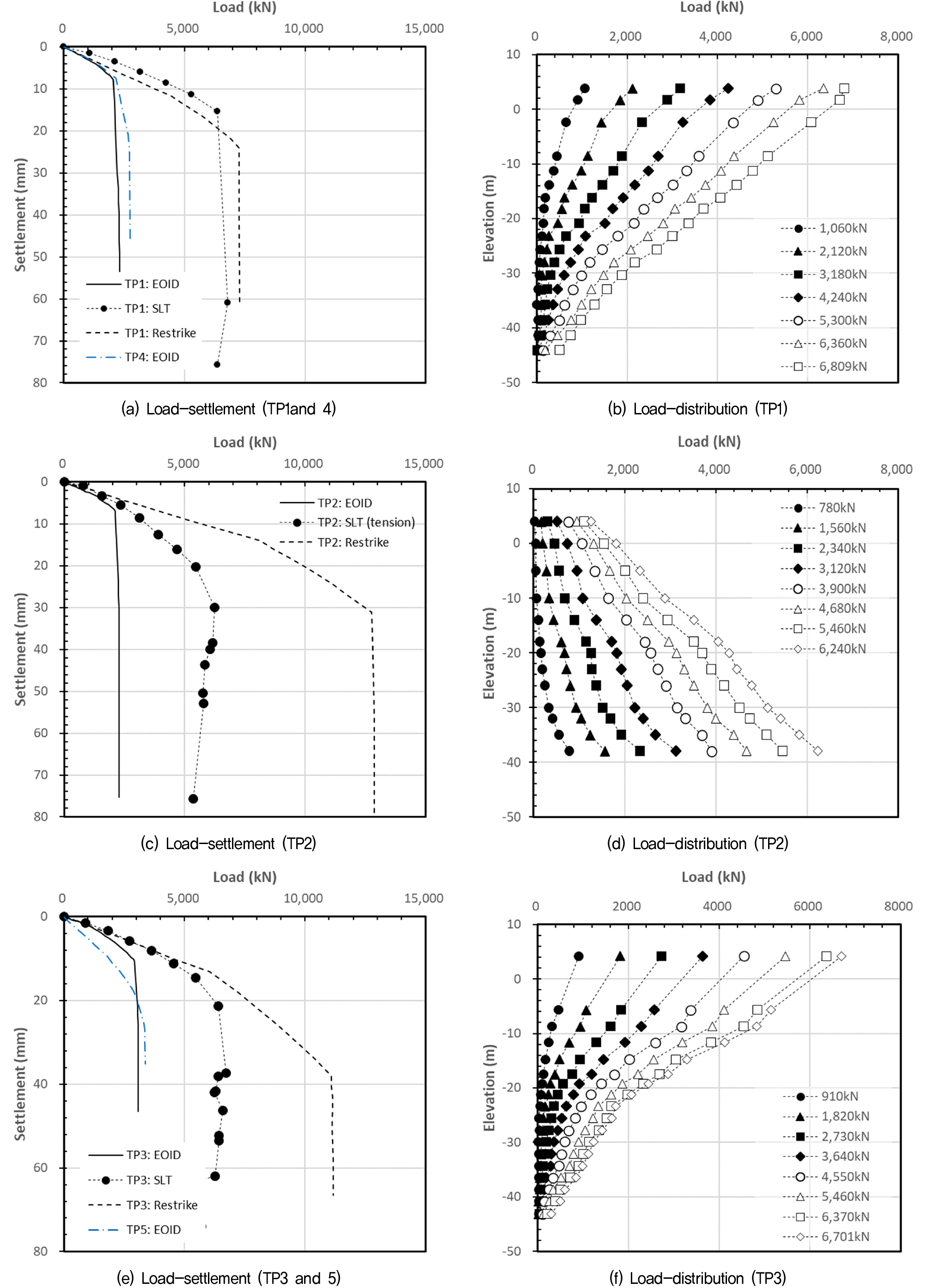
정재하시시험(static load test, SLT)은 점토지반의 set-up 효과를 감안하여 재항타 동재하시험 종료일로부터 최소 6주 이상 경과 후 동일한 시험말뚝 3본(TP1~3)을 대상으로 수행되었으며, 이 중 TP1과 TP3은 압축재하 TP2는 인발재하로 시험을 ASTM D 1143-81, ASTM D 3689-07(2013)에 따라 진행하였다. Fig. 5는 정재하시험을 통해 측정된 하중-침하 곡선을 시항타/재항타 동재하시험을 통해 측정된 결과와 함께 도시하였다. TP1의 경우 SLT와 restrike을 통해 측정된 하중-침하 곡선은 유사한 양상을 보였으나, TP2와 TP3의 경우 SLT보다 restrike을 통해 측정된 지지력이 크게 나타났다. TP1~3은 stiff clay가 우세한 유사한 또는 동일한 지반조건에서 시험이 시행되었으며 시험말뚝의 설계하중 및 제원을 고려하였을 때, TP2와 TP3의 restrike를 통해 측정된 주면 마찰력은 SLT 결과대비 매우 과다(최대 2배)하여 전체 경향성에서 벗어난 것으로 사료된다.
동재하시험은 충격하중을 통해 말뚝 선단에서 반사되어 상부로 전파되는 파동 신호를 분석하여 간접적으로 지지력을 산정하는 반면, SLT는 말뚝에 정적 하중을 점진적으로 가하여 실제 하중-침하 곡선을 측정하기에 일반적으로 참값으로 여긴다. 따라서 이러한 오차는 restrike시 시험말뚝에 부착된 게이지의 오작동, 편타에 의한 응력파의 품질 문제 등에 의해서 야기될 수 있으며, 그에 따른 지지력 차이가 매우 크게 발생 될 수 있음을 보여주는 사례이다. 따라서 시간경과에 따른 지지력 변화 측정시 restrike 만으로 수행시에는 면밀한 시험 수행 뿐 아니라 측정값의 큰 편차 발생 가능성을 대비하여 구조물의 중요도를 감안하여 충분한 시험수량을 계획하거나 SLT를 병행하는 방법도 필요시 고려되어야 한다.
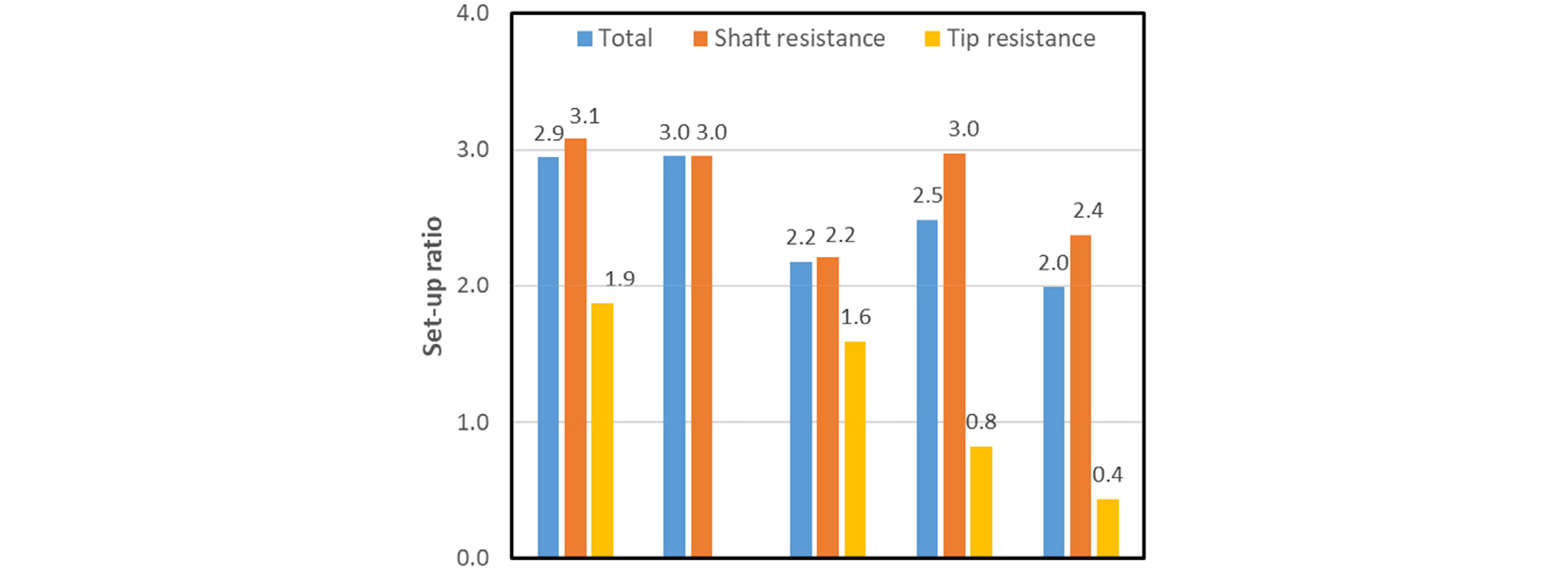
본 SLT에서는 wire type의 strain gauge를 말뚝 종방향 위치에 따라 2열로 부착하여 선단지지력과 주면마찰력을 분리 측정하였으며, 이를 동재하시험 결과와 비교하여 Table 6에 요약 정리하였다. 측정된 극한 선단지지력은 전체 지지력의 5~10% 정도로 동재하시험 결과와 같이 비중이 크지 않았으며, 대부분은 주면 마찰력으로 발현되는 것으로 나타났다. 3본 시험말뚝의 주면장을 고려한 단위 극한 주면마찰력은 45~53kN/m2으로 유사하게 나타났으며, EOID 지지력과 비교시 SUR(set-up ratio)은 2.2~3.1배 범위로 나타났다. 다만 앞서 3.2절에서 기술한 바와 같이 직경이 큰 TP1, 2, 4 시험말뚝의 EOID 지지력이 직경이 작은 TP3, 5보다 관입시 지반 교란 영향 등으로 더 낮게 나타나 SUR은 Fig. 6과 같이 더 크게 나타났다.
Table 6.
Comparison of dynamic and static load test results
선단지지력의 경우 시험말뚝 TP1과 TP2의 SUR은 1.6~1.9 정도 나타났으나, 선단지지력 비중이 전체 말뚝 지지력에 비해 10% 이내로 비중이 낮고, EOID의 선단지지력의 측정 오차범위를 고려하였을 때 이는 유의미한 값이라 볼 수 없다고 판단된다. 이는 시험말뚝 TP4와 TP5의 EOID 선단지지력이 오히려 SLT을 통한 TP1와 TP3 선단지지력 보다 크게 측정된 사실에서도 확인되며, 또한 충분한 고려 없이 EOID시 측정된 선단지지력을 적용시 오히려 실제보다 과대적용 할 수 있는 소지가 있음을 알 수 있다.
4. 동역학적 지지력 공식을 이용한 항타시공관리
단단한 하부 지층에 선단 지지되는 말뚝의 경우 지지력이 선단 지지층에 의해 좌우되고, 항타 관입량 자체가 선단 지지층 도달 후 급격히 감소하므로 소요 지지력에 맞는 항타 관입량을 산정하여 시공 관리하는 것은 신뢰성을 담보하기가 어렵다. 그러나 지층 변화에 따라 말뚝 길이 변화가 크게 발생하는 마찰말뚝의 경우에는 항타에 따른 선단 관입량이 점진적으로 감소하므로 소요 지지력을 만족하는 항타 관입량 또는 리바운드량을 이용한 동역학적 지지력 공식(항타공식)이 현장 항타 시공관리에 유용하게 사용될 수 있다. 이에 항타공식에는 많은 연구 제안들이 있었으며, 강관말뚝의 경우 Hiley 및 Danish 공식이 비교적 신뢰도가 높은 것으로 보고된 바 있다(Hong et al., 1997; Beresibo, 2021; Ramey and Johnson, 1979). 다만, 항타공식으로부터 산정된 지지력은 말뚝 관입(pile driving) 대한 지반의 동적 저항력을 의미하며 이는 말뚝의 정적 지지력(static load capacity)과는 차이가 있기 때문에 지반의 동적/정적 저항 관계에 불확실성으로 지지력 산정시 직접 적용에는 실질적으로 무리가 있다. 이에 본 현장의 경우 동재하시험과 정재하시험 결과를 함께 고려하여 Danish 항타공식(Rd)을 다음과 같이 수정(Rs)하여 항타 시공관리에 적용하였다.
여기서, α는 교정계수(calibration factor)로 EOID시 CAPWAP으로 산출된 시험말뚝의 동적 지지력(Rsi(TP))과 본래의 Danish식으로 산정된 시험말뚝의 동적 지지력(Rd(TP))의 비를 의미하며, 본 현장시험말뚝 TP1~TP5로부터 산출된 α의 경우 0.6~1.0으로 나타나 Danish식으로 산정된 동적 지지력값이 현장 동재하시험 값보다 다소 크게 나타남을 알 수 있다. α값 산정시 Danish식으로 산정된 시험말뚝의 지지력은 본 시험에서 측정된 실제 해머에너지와 효율의 중간값 0.8을 적용하였다.
St는 시간경과에 따른 지지력 증가비(Set-up ratio, SUR)로 정재하시험으로부터 얻은 지지력(Rs(TP))과 EOID시 CAPWAP으로 얻은 지지력(Rsi(TP))의 비를 의미한다. 앞서 3.4절에서 기술한 바와 SUR은 항타 시공시 지반 교란의 영향으로 말뚝 직경이 영향을 미치는 요소이나, 본 시험만으로 이를 정량화 하여 적용하기는 재하시험 횟수가 제한적이라 본 현장 시공에서는 전체 시험말뚝 5본의 평균 2.5(측정된 시험 값 범위 2.2~3.1)를 일괄 적용하였다.
본래의 Danish식(Rd)은 알려진 바와 같이 다음의 관계로 표현 가능하며(DS 415, 1998),
여기서, 해머 에너지(e)는 시험말뚝의 입력에너지(input hammer energy, EHT)와 전달 에너지(transferred hammer energy, EH)의 비로 앞서 회귀분석을 통해 도출된 식 (3)을 통해 산출할 수 있다. 또한 S는 EOID에서의 set-value로서 해머 타격 후 말뚝이 영구적으로 관입된 깊이 즉, 타격 전후 말뚝 두부의 변위 차이를 의미한다. Se는 elastic set으로 해머의 타격 에너지가 말뚝을 통해 전달될 때 말뚝과 주변 지반이 탄성적으로 압축되면서 발생하는 일시적인 변위를 나타내며, 다음과 같이 나타낼 수 있다(Olson and Flaate, 1967).
여기서, Lpile, Apile, Epile은 파일을 길이, 파일 선단의 단면적, 탄성계수를 각각 의미한다.
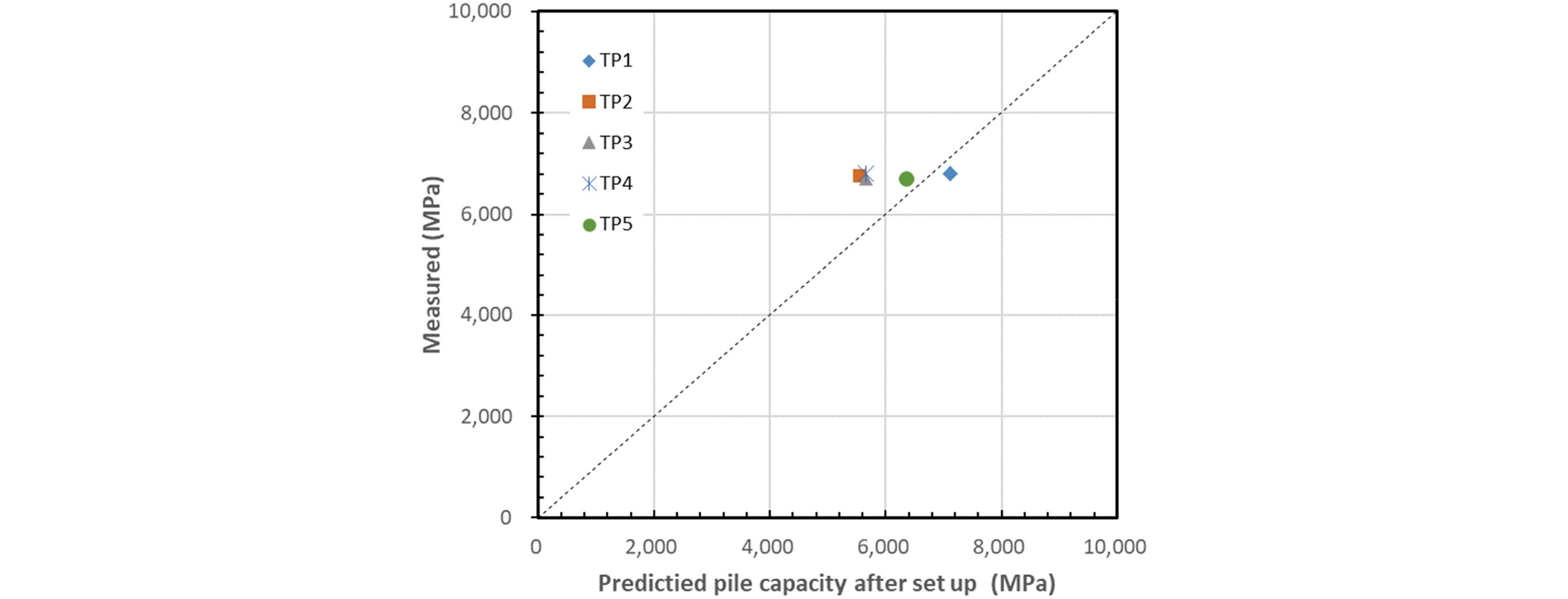
이와 같은 관계로부터 EOID시의 set value와 말뚝의 정적 지지력간의 관계를 도출할 수 있으며, 말뚝직경, 말뚝길이, 시공시 적용한 해머에 조건에 따른 말뚝의 정적 지지력을 간편하게 예측하여 시공관리가 가능하다. 수정된 항타공식을 통해 예측된 말뚝 지지력(Rs)과 정재하시험 결과를 비교한 결과는 Fig. 7에 도시하였다. Fig. 8은 이를 토대로 검토한 매개변수 결과이며, 동일한 set value을 가질 때 말뚝길이가 짧을수록 또는 말뚝의 단면적이 클수록 말뚝의 elastic set은 감소하므로 말뚝의 지지력(Rd)은 더 크게 나타남을 알 수 있다. 다만 set-value가 작아질수록 지지력 변화의 민감도가 상대적으로 크므로, 단단한 지층에 관입 되는 항타말뚝과 같이 set-value값이 작을 경우 측정시 보다 주의를 가져야 한다. 또한 본 연구에서 제안된 방법은 선단지지 말뚝과 같이 set-value 값이 지층 조건에 따라 급변하는 경우가 아닌 마찰 말뚝과 같이 지지력의 변화가 점진적으로 변하는 경우에 적절할 것으로 사료된다.
5. 결 론
본 연구에서는 베트남 중부 연안의 대심도 점토지반에 항타 시공된 마찰지지 강관 말뚝의 항타 시공관리 방법과 사례를 설명하였다. 현장 실무에서의 활용 용이성을 위하여 말뚝과 해머 제원만으로 산정 가능한 항타공식을 이용하였으며, 현장 적용성을 보완하기 위해 수행된 정/동적 재하시험의 결과를 고려하였다. 그 결과 다음과 같은 결론을 얻었다.
(1) 해머의 효율(e)은 항타말뚝의 지지력을 산정하는 주요 요소로써, 대심도 점토지반에서 유압해머의 효율은 70~80% 범위로 나타났으며, 램 낙하고(h)가 높아질수록 EMX는 선형적으로 증가하나 에너지 손실 또한 커져 해머 효율은 감소하는 것으로 나타났다. 반면 디젤해머 해머효율은 25~35%(평균30%) 정도로 확인되었으며, 편타 등 시공오차가 발생했을 때 효율이 크게 낮아질 수 있어 시공 관리시 면밀한 주의가 요구된다.
(2) 시항타 동재하시험을 통한 주면 마찰력 비교 검토결과, 해머타입(유압/디젤)에 따른 주면마찰력 차이는 나타나지 않았으나, 말뚝이 직경이 작을 수록 더 큰 단위 주면마찰력이 발현되었다. 이러한 차이는 항타 관입시 지반교란 측면에서 소구경이 상대적으로 유리하였으리라 추정되며, 이는 결과적으로 set-up ratio의 영향요소로 작용함을 확인하였다.
(3) 본 시험시공에서 측정된 선단지지력의 set-up ratio는 일부 시험말뚝에서는 측정되었으나, 대심도 마찰지지 강관말뚝에서는 선단지지력의 비중이 전체 말뚝 지지력에 비해 10% 이내로 비중이 낮고, EOID의 선단지지력의 측정 오차범위를 고려하였을 때 시간 효과에 따른 지지력 증가는 유의미하지 않는 것으로 판단된다.
(4) 지반의 동적/정적 저항 차이에 따른 불확실성 배제하고 현장 시공관리의 용이성 위하여 현장에서 실물 조건으로 시공된 시험말뚝의 재하시험 결과와 수정된 Danish 항타공식을 토대로 set value와 말뚝의 지지력간의 관계를 도출하였다. 단, 매개변수연구 결과, set-value가 작을수록 지지력 변화의 민감도는 크게 높아지므로 사용시 주의를 가져야 하며, 본 현장 지반과 같이 심도에 따라 지층 및 지반 물성 변화가 크지 않아 주면 지지력이 지반 심도에 따라 점진적으로 증가하는 마찰지지 말뚝의 경우에 제한적으로 적용 가능할 것으로 사료된다.