1. 서 론
2. 분석대상의 재료조건과 시험조건
3. 전단탄성계수 감소곡선
3.1 정규화 전단탄성계수 감소곡선 산정식 제안
3.2 정규화 전단탄성계수 감소곡선 산정식에 의한 보강효과 분석
4. 감쇠비 곡선 산정식
4.1 감쇠비 곡선 산정식 제안
4.2 감쇠비 곡선 산정식에 의한 보강효과 분석
5. 결 론
1. 서 론
비닐은 플라스틱과 함께 일상생활에서 늘 만나게 되는 필수적인 물질로 각종 포장재, 방수재, 농업용 하우스 등에 이용되어 인류 삶의 질을 높여왔다. 이러한 유용성에도 불구하고 비닐의 사용 후 처리문제는 전 세계적인 환경문제가 되고 있다. 폐비닐의 경우, 500년 이상으로 추정되는 긴 부패시간으로 매립처분은 효과가 없으며 소각처리 시에는 심각한 대기오염 문제가 발생한다. 따라서 폐비닐을 재활용하는 연구와 기술개발이 다양한 분야에서 이루어지고 있으며, 지반공학 분야에서는 주로 지반보강재로의 적용성을 연구하고 있다. 관련된 기존 연구로는 폴리에틸렌수지의 비닐하우스용 필름(Kim et al., 2000) 혹은 고밀도 폴리에틸렌(HDPE) 비닐(Chebet et al., 2014)을 스트립 형태로 잘라 지반보강재로 적용하여 투수성, 강도특성, 하중지지력을 분석한 연구가 대표적이다. 또한 Kim(2017)은 하우스용 폐비닐로 만든 골재를 아스콘에 적용한 연구를 수행하였다. 최근에는 농촌에서 하우스용 필름으로 많이 사용되는 저밀도 폴리에틸렌(LDPE) 비닐을 스트립 형태로 잘라 상대밀도 40%와 60%인 중간 모래(medium sand)의 보강재로 적용하여 정적 및 동적거동을 분석한 연구가 수행된 바 있다(Yu et al., 2018). 이렇듯 저밀도, 저중량, 고인장력 등의 특성을 지닌 폴리에틸렌 비닐은 지반의 강도증가를 위한 보강재로서의 적용성이 기존연구를 통해 입증되었으나, 제작비용이 저렴한 스트립 형태로 적용된 사례는 상대적으로 드문 실정이다(Phanikumar, 2011). 반면 유사한 성상의 HDPE 플라스틱을 스트립 형태의 지반보강재로 적용한 연구는 상대적으로 활발히 진행되어 왔으며 기초지반 및 노상토의 지지력을 향상시킨 활용사례가 있다(Consoli et al., 2003; Venkatappa et al., 2004). 폴리에틸렌 비닐은 저비용이며 재활용 비닐의 적용도 가능하여 시멘트와 혼용할 경우 적은 비용으로 보강효과를 더욱 개선시킬 수 있다(Ahmed, 2012). 본 연구에서는 전술한 Yu et al.(2018)의 연구결과 중 동적거동 분석에 이용된 공진주시험 결과에 대한 분석을 통해 비닐스트립-시멘트로 보강된 모래시편의 전단탄성계수와 감쇠비를 추정할 수 있는 함수식을 제안하고자 한다. 중간~느슨한 양입도의 모래를 대상으로 한 Yu et al.(2018)의 연구에서 비닐스트립-시멘트의 혼합 보강으로 인한 일축압축강도 증가율은 무보강 대비 2.2~2.8이었고 비닐스트립만의 영향으로도 1.2~1.3배 증가하는 보강효과를 확인하였으며, 본 연구에서는 동적보강효과에 대해 분석하고자 한다.
정규화 전단탄성계수 감소곡선은 쌍곡선(hyperbolic) 함수를 기본형으로 하며, 함수식 제안에 관한 기존 연구는 다음과 같다. Rollins et al.(1998)은 자갈의 정규화 전단탄성계수 감소곡선 산정식을 제안하였다. 정규화 전단탄성계수 감소곡선 산정식이 전단탄성계수 뿐 만 아니라 전단변형률도 기준변형률(γr, reference strain)로 정규화한 형태인데 반해 Rollins는 정규화하지 않은 전단변형률의 함수로 전단탄성계수비를 산정하는 식을 제안하였다. Oztoprak et al.(2013)은 광범위한 기존 실험결과들을 수집한 데이터베이스 분석을 통해 수정 쌍곡선(modified hyperbolic) 산정식을 제안하였다. Zhou et al.(2017)은 사력(rockfill)재에 대해 power-power 함수 형태의 정규화 전단탄성계수 감소곡선 산정식을 제안하였으나, 산정식의 계수값에 따라 쌍곡선 형상을 벗어날 수 있는 한계점이 있다. Araei et al.(2017)은 하중주파수를 고려한 산정식을, Wang et al.(2019)은 재활용 고로슬래그의 정규화 전단탄성계수 감소곡선 산정식을 제안하였다. 반면 감쇠비 곡선은 역쌍곡선 함수를 기본형으로 하는데, 정규화 전단탄성계수 감소곡선에 비해 산정식 제안에 관한 기존 연구가 상대적으로 부족한 편이다. 전술한 전단탄성계수 감소곡선 산정식의 기존연구에서 언급한 Rollins et al.(1998), Araei et al.(2017) 등이 감쇠비곡선 산정식을 제안한 바 있다.
본 연구에서는 비닐스트립-시멘트로 보강된 모래시편에 대한 Yu et al.(2018)의 공진주 시험 결과를 이용하여 정규화 전단탄성계수 감소곡선과 감쇠비 곡선 산정식을 보강조건(비닐스트립 혼합비와 시멘트 혼합비)과 구속압조건의 함수식으로 제안하였다. 제안된 식을 이용하면 공진주시험을 수행하지 않고도 비닐스트립-시멘트로 보강된 모래지반의 정규화 전단탄성계수 감소곡선과 감쇠비 곡선을 간단히 추정할 수 있으므로 시험에 요구되는 비용과 시간을 절감하는 효과를 볼 수 있을 것으로 기대된다.
2. 분석대상의 재료조건과 시험조건
본 연구에서 분석한 비닐스트립-시멘트 보강 모래시편의 재료조건과 공진주시험용 시편조건은 Yu et al.(2018)에 자세히 기술되어 있으며 본 논문에서는 기본적인 사항만을 정리하였다. Table 1은 보강대상인 흙과 보강재인 비닐스트립, 시멘트의 재료조건을 정리한 것이다.
Table 1.
Material properties (Yu et al., 2018)
전단탄성계수와 감쇠비 측정을 위한 공진주시험의 시편조건과 시험조건은 Table 2와 같다. Table 2의 비닐스트립 혼합비(Vc, vinyl strip content)와 시멘트 혼합비(Cc, cement content)는 모두 중량비이다.
Table 2.
Conditions of resonant-column test (Yu et al., 2018)
Table 2에서 보듯이 본 연구에서는 다양한 보강조건과 구속압조건에 대한 총 36개 공진주시험 자료를 분석하였다. 구속압을 가한 상태에서 진동주파수를 13단계로 증가시켜가며 각 주파수 단계마다 전단탄성계수와 감쇠비를 측정하고 구속압을 순차적으로 증가시키며 가진과정을 반복하는 다단계 시험방식으로 진행된 공진주시험 결과(Yu et al., 2018)를 본 연구에 적용하였다.
3. 전단탄성계수 감소곡선
3.1 정규화 전단탄성계수 감소곡선 산정식 제안
정규화 전단탄성계수 감소곡선을 모사하기 위해서는 Hardin et al.(1972)이 제안한 쌍곡선 모델(hyperbolic model)이 가장 널리 사용된다. 본 연구에서는 비닐스트립-시멘트로 보강된 모래시편의 전단탄성계수 감소곡선의 함수식을 제안하기 위해 조립토(Araei et al., 2017; Zhou et al., 2017)와 보강토(Liao et al., 2013)에 대한 전단탄성계수 감소곡선의 모사에 적합한 것으로 알려진 수정 쌍곡선 모델(Darendeli, 2001)을 적용하였으며, 기본식은 식 (1)과 같다.
여기서 G=전단변형률에 따른 전단탄성계수, G0=최대전단탄성계수, γ=전단변형률, γr=기준 전단변형률(reference shear strain), α=곡선조정계수
식 (1)은 2계수 모델로 γr은 G/G0=0.5에 해당하는 전단변형률이고 α는 시험결과에 곡선형상을 맞추기 위한 조정계수이다. 본 연구에서는 다양한 보강조건과 구속압조건으로 수행한 36개 시편에 대한 공진주시험 결과로 얻어진 전단탄성계수 측정값에 대해 식 (1)을 기반으로 회귀분석을 실시하여 γr과 α를 추정하였다. 전단탄성계수를 최대전단탄성계수로 정규화하면 구속압의 영향은 무시할 수 있을 만큼 미미해지며, 따라서 γr과 α는 보강조건의 영향만을 받게 된다. 보강조건에 따른 γr과 α 추정값을 Table 3에 정리하였다. 추정값을 식 (1)에 적용하여 계산된 정규화 전단탄성계수를 36개 시험 측정값과 비교한 결과, 결정계수 (R2)의 평균값은 0.965, 최소값은 0.933으로 매우 높은 신뢰도를 보여주었다.
Table 3.
Estimated values of coefficients γr and α
Table 3에서 보듯이 보강조건이 강화될수록, 즉 Vc와 Cc가 증가할수록 γr은 증가하는 반면 α는 반대의 경향을 보임을 알 수 있다. 이러한 경향을 바탕으로 Table 3의 추정값에 대한 회귀분석을 수행하여 보강조건에 따른 γr과 α값의 산정식을 식 (2)와 같이 제안하였다.
여기서 Cc, Vc, γr의 단위는 모두 %
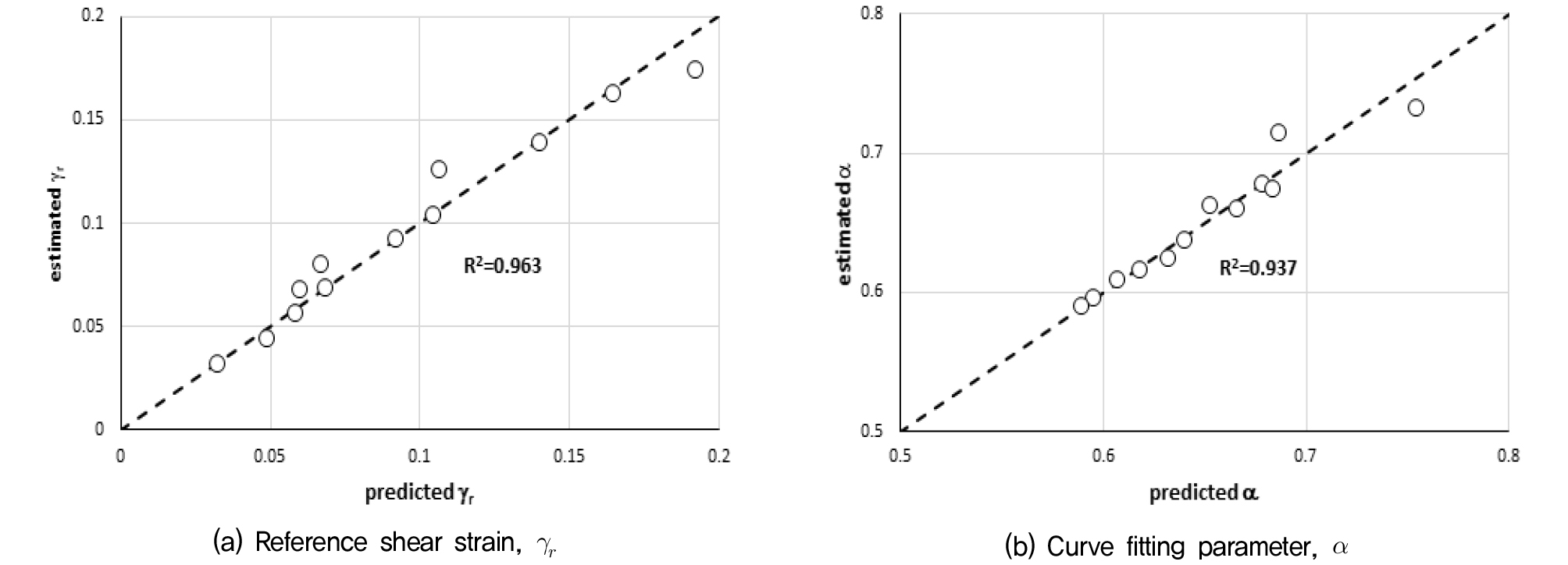
Fig. 1은 식 (2)에 의해 산정된 γr, α값과 시험결과로부터 추정된 Table 3의 γr, α값을 비교한 것으로 두 계수 모두 0.963과 0.937의 높은 결정계수를 보여주고 있다.
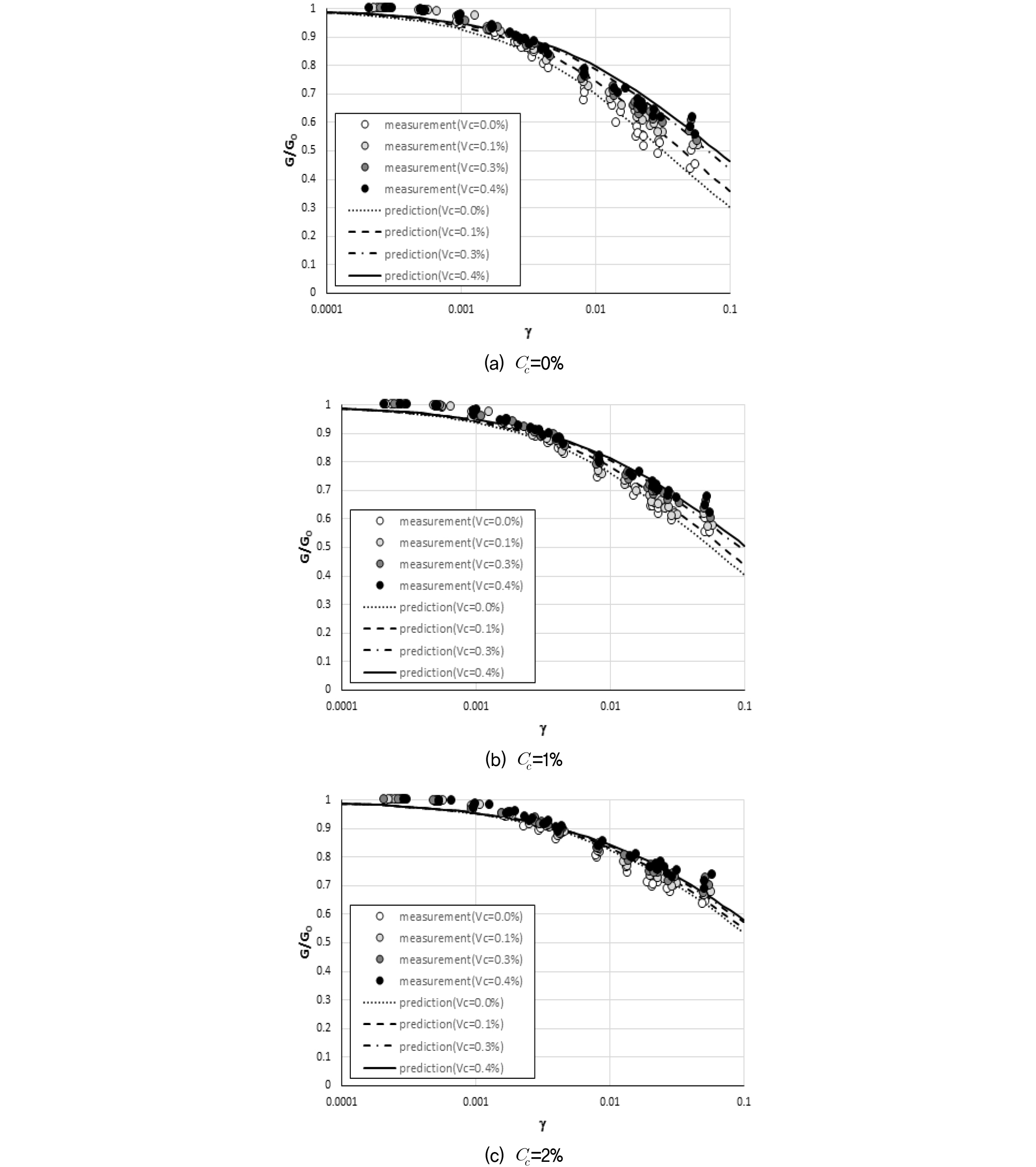
따라서 식 (2)를 식 (1)에 적용하면 보강조건에 따른 정규화 전단탄성계수 감소곡선을 도시할 수 있다. 본 연구에서 분석한 공진주시험 조건(Table 2)에서의 정규화 전단탄성계수 시험결과와 제안 함수식을 적용하여 산정된 감소곡선을 Cc=0%, 1%, 2%인 경우로 분류하여 Fig. 2에 도시하였다.
Fig. 2의 시험 측정값과 함수식 산정값을 비교·분석한 결과, 결정계수는 0.9 이상(R2=0.908~0.983)으로 산정 함수식의 신뢰도가 높음을 알 수 있다.
정규화 전단탄성계수 감소곡선 함수식 (1)에 최대전단탄성계수를 곱해주면 전단탄성계수(G)와 전단변형률(γ)의 관계를 나타내는 전단탄성계수 감소곡선을 얻게 된다. 최대전단탄성계수는 실내 혹은 현장시험을 통해 획득하거나 경험식을 이용하여 산정할 수 있다. 비닐스트립-시멘트 혼합 모래시편에 대한 최대전단탄성계수 산정식은 이미 제안된 바 있으며(Yu et al., 2018의 식 (2)), 해당 제안식에 본 연구에서 분석한 시험조건(상대밀도=0.4, 간극비=0.96, 양생기간=28일)을 적용하면 식 (3)과 같은 비닐스트립-시멘트로 보강된 느슨한 중간 모래의 최대전단탄성계수 산정식을 도출할 수 있다.
여기서 σc=구속응력(kPa), G0는 MPa, Cc와 Vc는 %
따라서 식 (1), (2), (3)을 연계하면 실무에서 필요한 보강조건과 구속압조건에 따른 전단탄성계수 감소곡선을 산정할 수 있다.
3.2 정규화 전단탄성계수 감소곡선 산정식에 의한 보강효과 분석
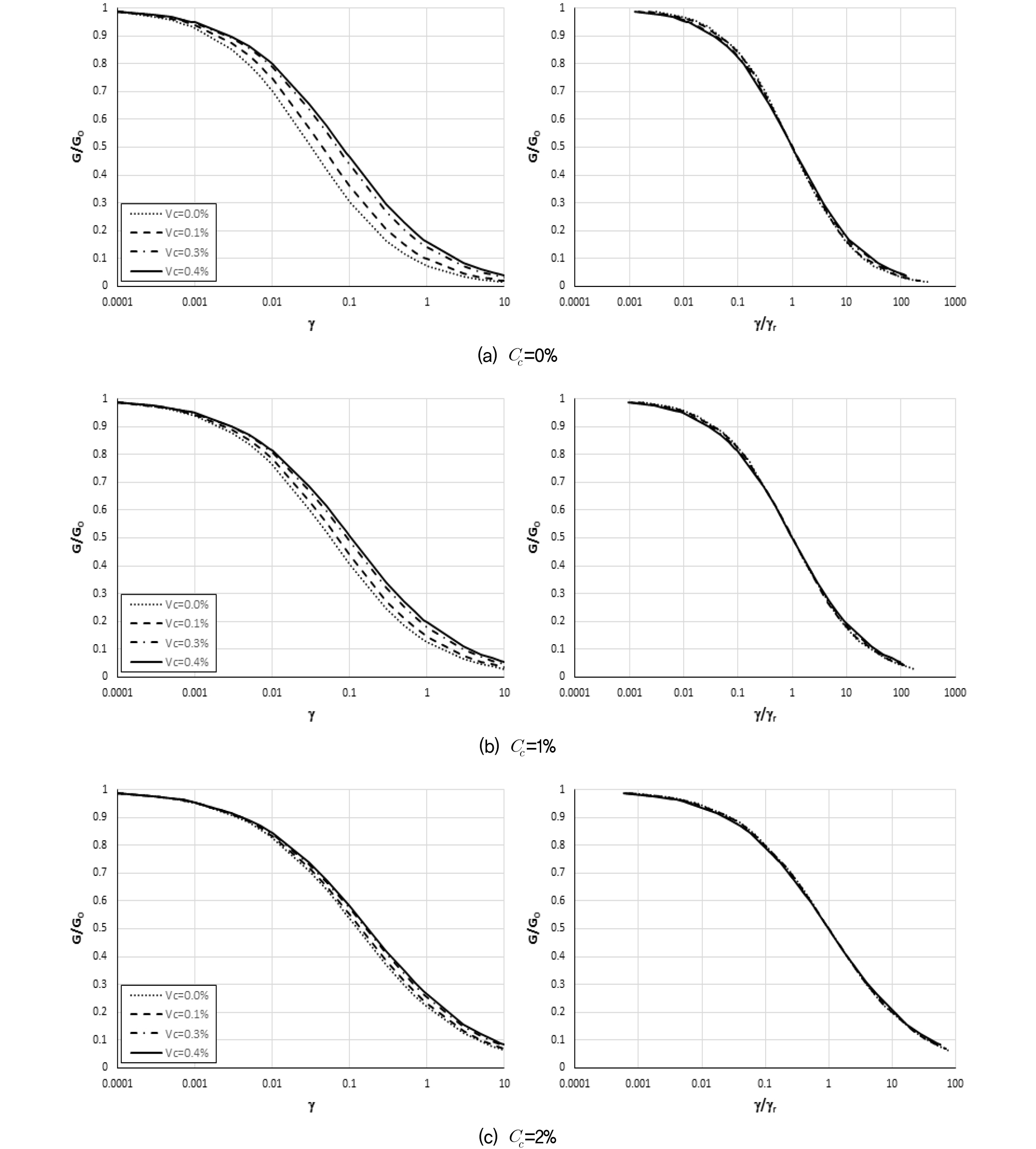
Fig. 3은 제안된 정규화 전단탄성계수 감소곡선 함수식을 Cc=0%, 1%, 2%인 경우에 대해 전단변형률 0.0001%~10%까지 확장·적용하여 도시한 것이다.
Fig. 3에서 좌측의 곡선은 G/G0-γ의 관계를 그리고 우측의 곡선은 전단변형률을 기준변형률로 정규화한 G/G0-γ/γr의 관계를 보여주고 있다. G/G0-γ곡선을 보면 Cc가 동일한 경우, Vc가 증가할수록 정규화 전단탄성계수가 증가하는 현상을 잘 반영하고 있다. 또한 같은 곡선에서 Cc가 증가할수록 비닐스트립에 의한 보강효과가 감소하는 경향을 보여주는데 이는 Cc가 증가할수록 시멘트에 의한 보강효과가 지배적이 되어 비닐스트립의 영향이 상대적으로 감소하여 발생하는 현상을 반영하는 것으로 판단된다. 반면 G/G0-γ/γr곡선은 Vc와 무관하게 동일한 Cc에서는 하나의 곡선으로 수렴하는 양상을 보인다. 이는 Vc 증가에 따른 기준변형률(γr)의 증가가 주원인으로 판단된다. Table 3과 식 (2)에서 보듯이 Vc가 증가할수록 기준변형률(γr)이 증가하고 따라서 정규화된 전단변형률 γ/γr은 감소하여 곡선이 좌측으로 이동하게 되는 반면 곡선조정계수(α)는 감소하여 곡선이 완만해지나 그 영향은 Table 3에서 보듯이 상대적으로 미미한 편이다.
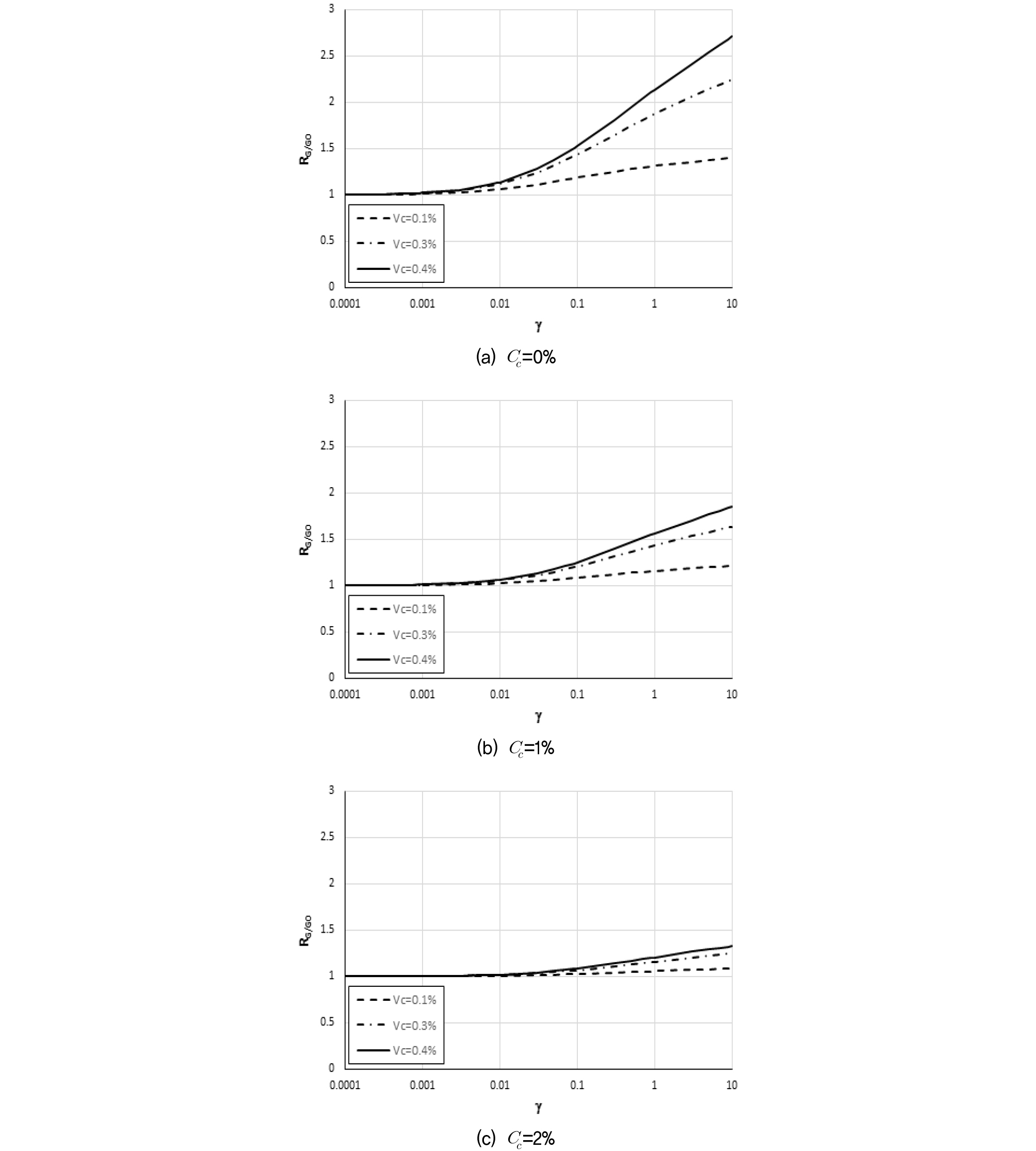
비닐스트립의 영향이 본 연구에서 제안한 정규화 전단탄성계수 산정식에 반영되는 양상을 살펴보기 위해, 동일한 Cc 조건에서 비닐스트립이 없는 경우에 대한 있는 경우의 정규화 전단탄성계수 변화비 RG/G0()를 분석하였다. Fig. 4는 전단변형율과 RG/G0의 관계를 비닐스트립 혼합비 및 시멘트 혼합비에 따라 도시한 것이다.
Fig. 4에서 보듯이 산정식에 의한 정규화 전단탄성계수 변화비는 1 이상이며 전단변형이 진행될수록 증가하는 경향을 보여 전단저항에 의한 비닐스트립의 보강효과를 반영하고 있다. 전단변형률 10%에서 최대 2.7배(Cc=0%, Vc=0.4%), 최소 1.09배(Cc=2%, Vc=0.1%) 증가하는 것으로 산정되었으나, 이는 공진주시험의 변형률 범위를 훨씬 상회하는 대변형률에서의 증가율로서 파괴가 발생하지 않는다는 전제에서의 예측값이다. 공진주시험의 일반적인 최대 변형률인 0.1%에서의 RG/G0를 살펴보면 최대 1.53(Cc=0%, Vc=0.4%), 최소 1.03(Cc=2%, Vc=0.1%)으로 나타났다. 제안된 산정식은 Cc가 증가할수록 동일한 Vc에 대한 RG/G0의 감소를 보여주는데, 특히 Cc=2% 경우 RG/G0=1.03~1.08의 범위로 비닐스트립의 보강효과가 미미한 것으로 해석될 수 있다. 그러나 이는 정규화된 전단탄성계수의 증가율이 미미한 것으로, 실제 동적해석에 필요한 전단탄성계수의 증가율을 분석할 필요가 있다.
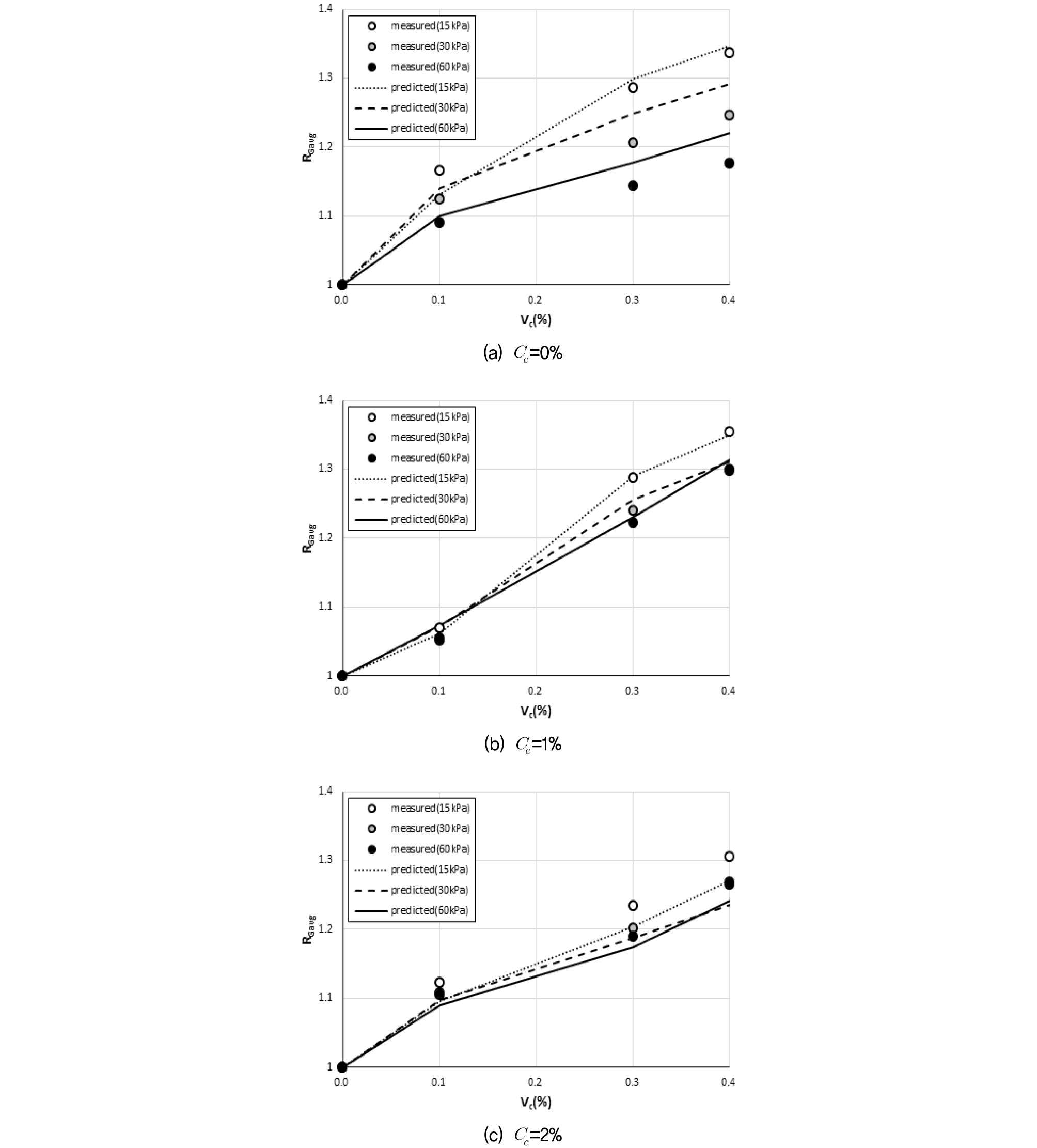
Fig. 5는 동일한 Cc 조건에서 비닐스트립이 없는 경우에 대한 있는 경우의 전단탄성계수 평균변화비, RGavg()과 비닐스트립 혼합비의 관계를 구속압 및 시멘트 혼합비에 따라 측정값과 제안식 산정값으로부터 계산된 RGavg값을 비교하여 도시한 것이다. 전단탄성계수는 보강조건과 전단변형률 뿐 만 아니라 구속압의 영향을 받으므로 모든 영향인자에 대한 전단탄성계수 변화비를 도시하기에는 어려움이 있다. 따라서 비닐스트립에 의한 전단탄성계수의 변화가 본 연구의 산정식에 반영되는 평균적인 양상을 살펴보기 위해 Yu et al.(2018)이 수행한 공진주시험의 전단변형률 범위(0.0001~0.1%) 내 전단탄성계수의 평균값을 이용하였다.
전단탄성계수는 제안식에 의해 산정된 정규화 전단탄성계수와 공진주시험 결과(Yu et al., 2018)로 측정된 최대전단탄성계수의 곱으로 산정되었다. Fig. 5에서 보듯이 모든 조건에서 Vc가 증가할수록 측정값과 산정값의 RGavg 모두 증가함을 보이고 있어, 제안식은 비닐스트립에 의한 보강효과를 반영하고 있다. Cc=2% 조건에서도 Vc=0.1%, 0.3%, 0.4%에 대해 측정값과 산정식에 의한 RGavg는 각각 1.11, 1.21, 1.28과 1.09, 1.19, 1.25로 제안된 산정식은 비닐스트립에 의한 전단탄성계수의 뚜렷한 증가를 반영하고 있다.
4. 감쇠비 곡선 산정식
4.1 감쇠비 곡선 산정식 제안
감쇠비는 전단변형률 증가에 따른 전단탄성계수 감소와 연계하여 산정되어야 하며, 무변형 상태에서의 최소감쇠비(Dmin)을 고려한 감쇠비 곡선식은 식 (4)와 같다(Yoshida, 2015).
여기서 Dmax=최대감쇠비, Dmin=최소감쇠비
식 (4)의 Dmax와 Dmin은 감쇠비 곡선의 위치와 형상을 규정하는 계수로서 본 연구의 분석대상인 비닐스트립-시멘트로 보강된 느슨한 중간 모래의 감쇠비 산정식을 제안하기 위해서는 우선 보강조건 및 구속압조건에 따른 값을 추정해야 한다. 이를 위해 Yu et al.(2018)의 공진주시험 결과로 획득한 감쇠비 측정값에 대해 식 (4)를 기반으로 회귀분석을 실시하여 Dmax와 Dmin을 추정하였으며 그 결과를 Table 4에 정리하였다.
감쇠비는 최대 혹은 최소값으로 정규화된 값이 아니므로 구속압의 영향을 고려해야 한다. Table 4의 추정값들에 대해 Cc, Vc, σc를 독립변수로 회귀분석을 수행하여 Dmax와 Dmin의 산정식을 식 (5)와 같이 제안하였다.
Table 4.
Estimated values of Dmax and Dmin
여기서 Pa=대기압=101.3kPa, Cc와 Vc는 무차원
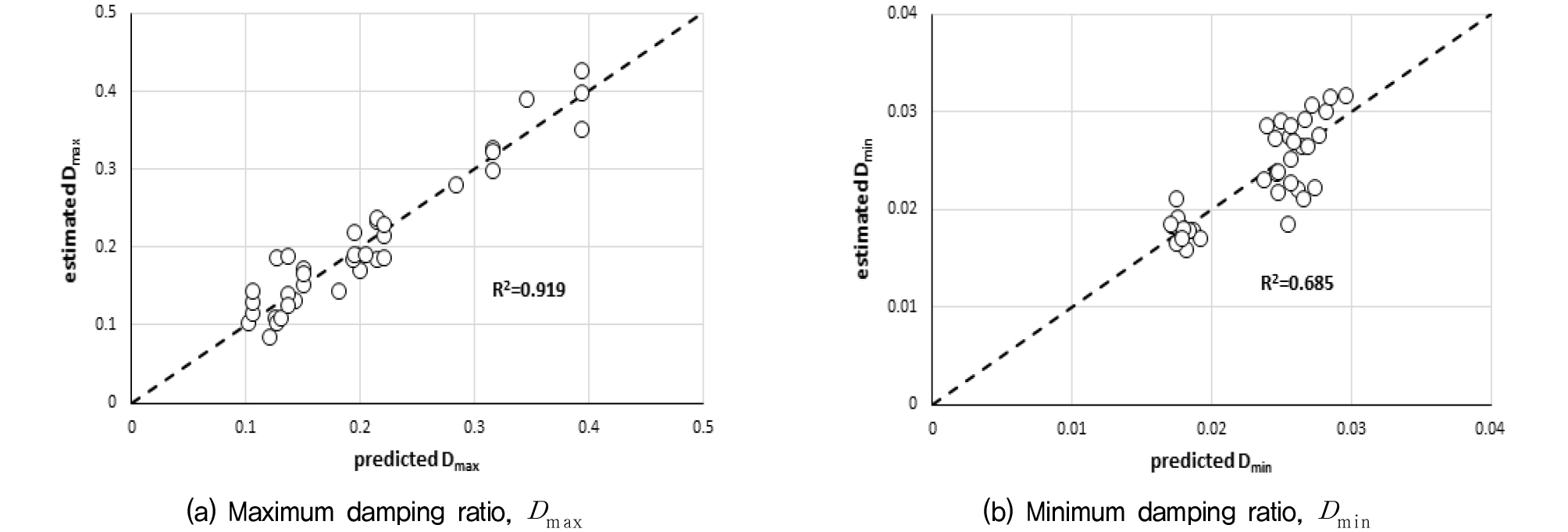
식 (5)에는 구속압이 포함되어 모든 변수를 무차원화하는 것이 바람직하며 이를 위해 구속압은 대기압으로 정규화하였다. 식 (5)에 의해 산정된 Dmax, Dmin과 시험결과로부터 추정된 Table 4의 Dmax, Dmin을 비교한 결과를 Fig. 6에 도시하였으며, 두 계수 각각 0.919와 0.685의 결정계수를 보여주었다.
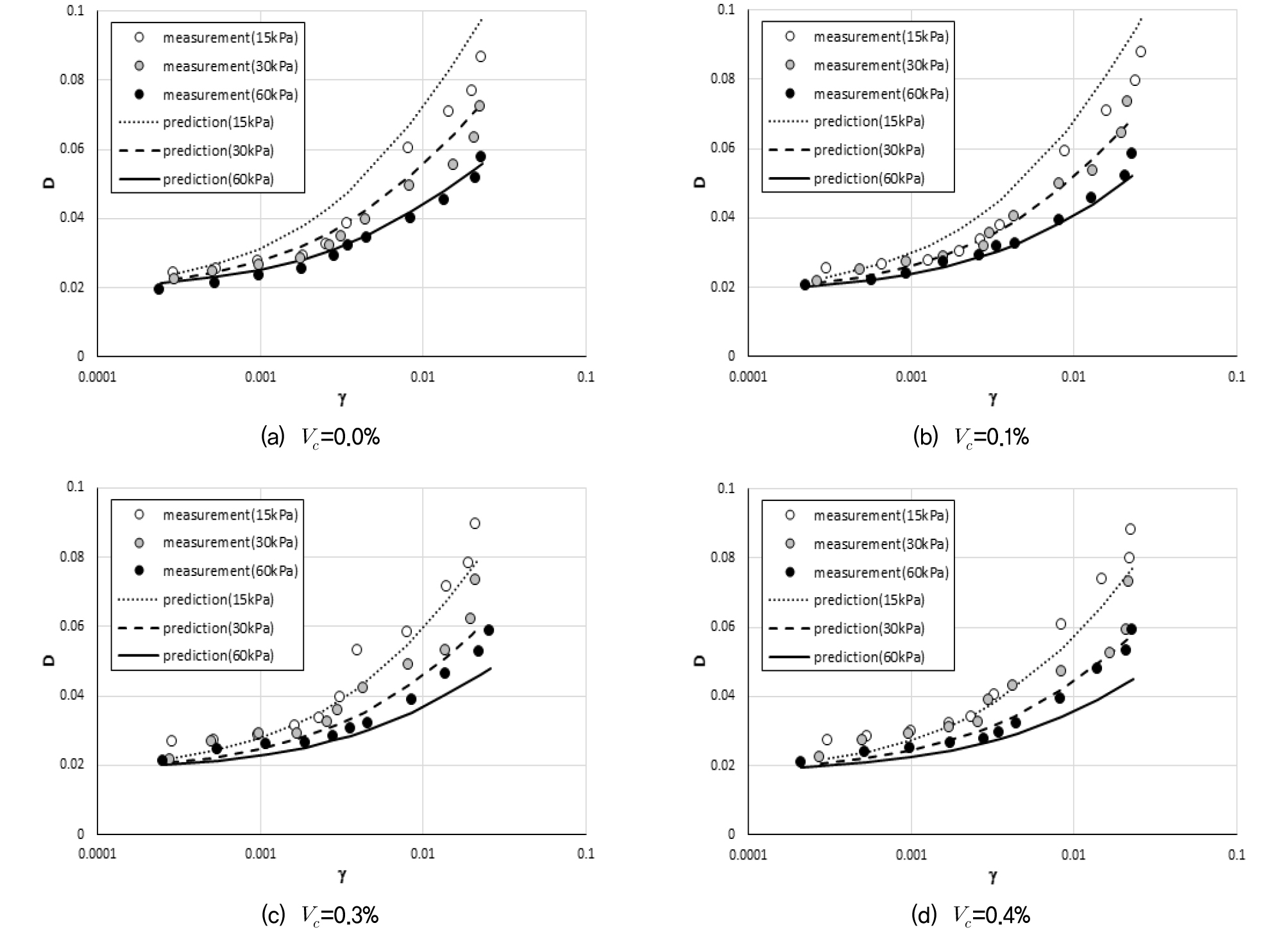
Dmin 산정식 (5b)의 결정계수가 상당히 낮으나 최소감쇠비는 매우 작은 값으로 감쇠비 곡선 산정에 있어 큰 영향요소는 아닌 것으로 판단된다. 식 (1), (2), (5)를 식 (4)에 적용하면 보강조건과 구속압조건에 따른 감쇠비 곡선을 도시할 수 있다. 일례로 Fig. 7은 시멘트 없이 비닐스트립으로만 보강된 경우(Cc=0%)에 대한 감쇠비 측정값과 제안된 식을 통해 산정된 감쇠비 곡선을 본 연구에서 분석한 공진주시험 범위에서 비교한 것이다.
Fig. 7에서 보듯이 구속압이 증가할수록 감쇠비는 감소함을 알 수 있다. 이는 구속압으로 인해 시편의 변형이 제어되어 내부에너지 소산이 감소하여 발생하는 현상이며, 구속압 증가에 따른 전단탄성계수의 증가도 같은 이유로 설명된다. 반면 Fig. 7로부터 비닐스트립이 감쇠비에 미치는 영향을 살펴보면 측정값은 뚜렷한 차이가 관찰되지 않으나 산정식에 의한 감쇠비 곡선은 Vc 증가에 따라 감쇠비의 미미한 감소가 관측되어 비닐스트립의 보강효과가 제안된 산정식에 반영된 것으로 보인다. 그러나 Table 4의 Cc=0%에 대한 Dmax 추정값의 변화를 보면 구속압이 동일한 경우 최대감쇠비는 Vc가 증가함에 따라 함께 증가하는 경향을 보이고 산정식에 의한 Dmax값도 동일한 경향을 보인다. 이는 Dmax에 해당하는 변형률에서는 비닐스트립과 흙입자 사이에 활동이 발생하여 내부에너지 소산이 증가하고 감쇠비가 증가하는 것으로 판단된다. 따라서 비닐스트립만으로 보강된(Cc=0%) 시편의 경우, 변형률이 작은 구간에서는 비닐스트립이 감쇠비를 미미하게 감소시키는 역할을 하지만 비닐스트립과 흙입자 사이의 활동이 발생하는 변형률을 넘어서면 비닐스트립이 감쇠비를 증가시키는 역할을 하게 되는 것으로 판단되며 제안된 산정식은 이러한 현상을 반영하고 있다.
4.2 감쇠비 곡선 산정식에 의한 보강효과 분석
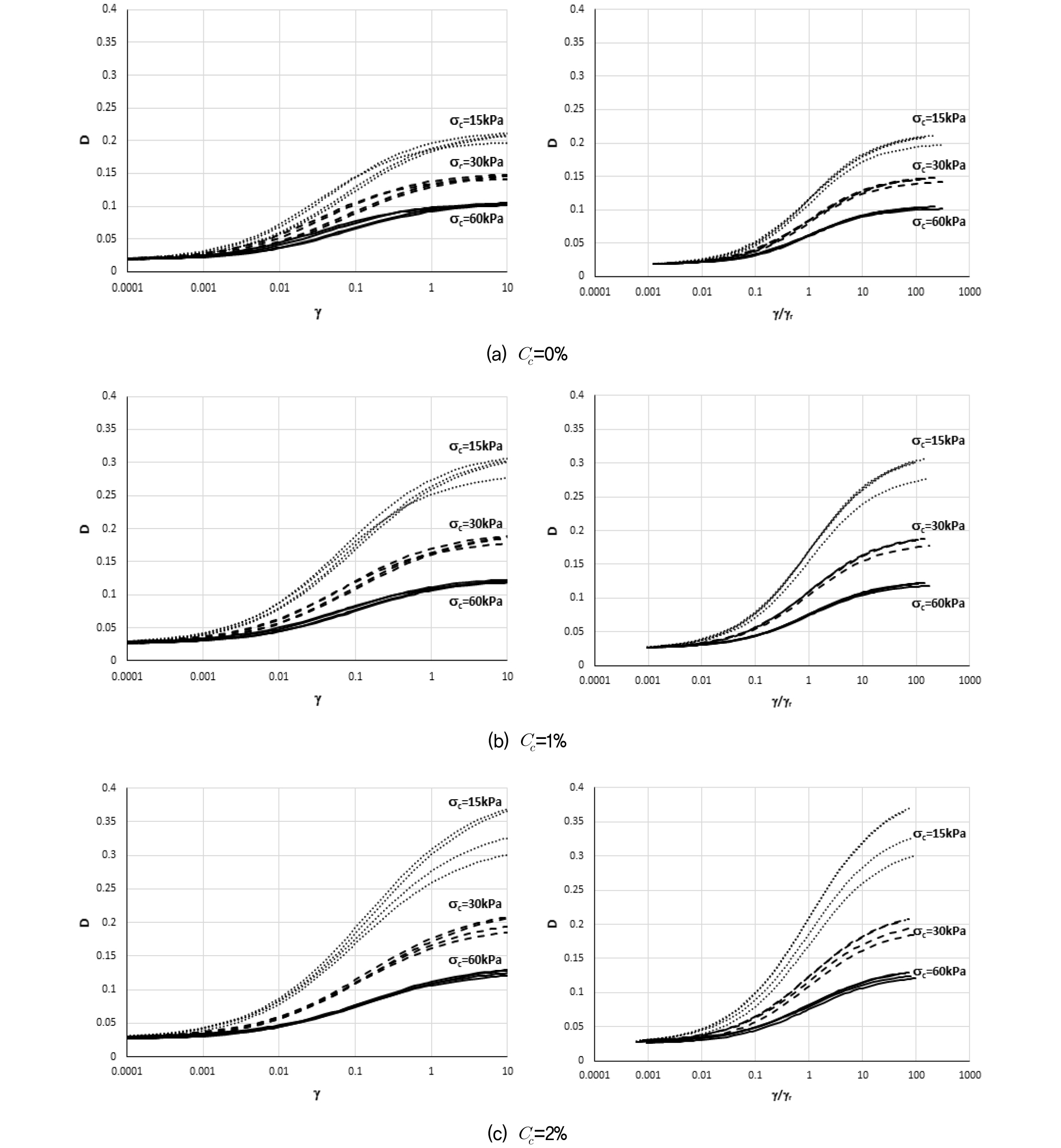
Fig. 8은 제안된 감쇠비곡선 산정식을 Cc=0%, 1%, 2%인 경우에 대해 전단변형률 0.0001%~10%까지 확장·적용하여 도시한 것이다.
Fig. 8에서 좌측의 곡선은 D-γ의 관계를 그리고 우측의 곡선은 전단변형률을 기준변형률로 정규화한 D-γ/γr의 관계를 보여주고 있다. 동일한 구속압에 대해 4개씩의 곡선이 도시되어 있는데 이는 Vc에 따른 차이이다. Vc에 따른 감쇠비의 차이는 Cc가 증가할수록 뚜렷해지는 것을 볼 수 있는데, 이는 비닐스트립과 시멘트 간의 상호작용으로 인한 내부에너지 소산양상이 변화된 것으로 판단된다. 또한 Fig. 8에서 Cc의 증가에 따른 감쇠비의 뚜렷한 증가를 볼 수 있는데, 이는 본 연구에 적용된 시멘트 혼합비로 설명될 수 있다. 본 연구의 Cc는 최대 2%로 흙입자와 비닐스트립을 부착시켜 강성을 증가시키기에는 부족한 양으로 최대 Cc인 2%를 적용하더라도 시멘트 입자가 흙입자와 비닐스트립의 표면을 코팅하는 정도의 양으로 판단된다. 따라서 시멘트가 시편의 강성을 증가시키고 감쇠비를 감소시키는 역할을 하는 것이 아니고 흙입자와 비닐스트립의 표면을 거칠게 만들어 내부에너지 소산을 촉진시키는, 즉 감쇠비를 증가시키는 역할을 하는 것으로 판단된다. 이는 시멘트 보강토의 감쇠비 특성에 관한 기존 연구결과와도 일치한다(Chiang et al., 1972; Saxena et al., 1987; Pantazopoulos et al., 2012; Thomas et al., 2020). 또한 Fig. 3의 정규화 전단탄성계수 감소곡선에서와 같이 전단변형률을 기준변형률로 정규화한 D-γ/γr곡선이 D-γ 보다 하나의 곡선으로 수렴하는, 즉 Vc의 영향이 약하게 나타나는 것이 관측되지만 그 차이는 미미하며 감쇠비 곡선에서는 구속압의 영향이 고려되기 때문인 것으로 판단된다.
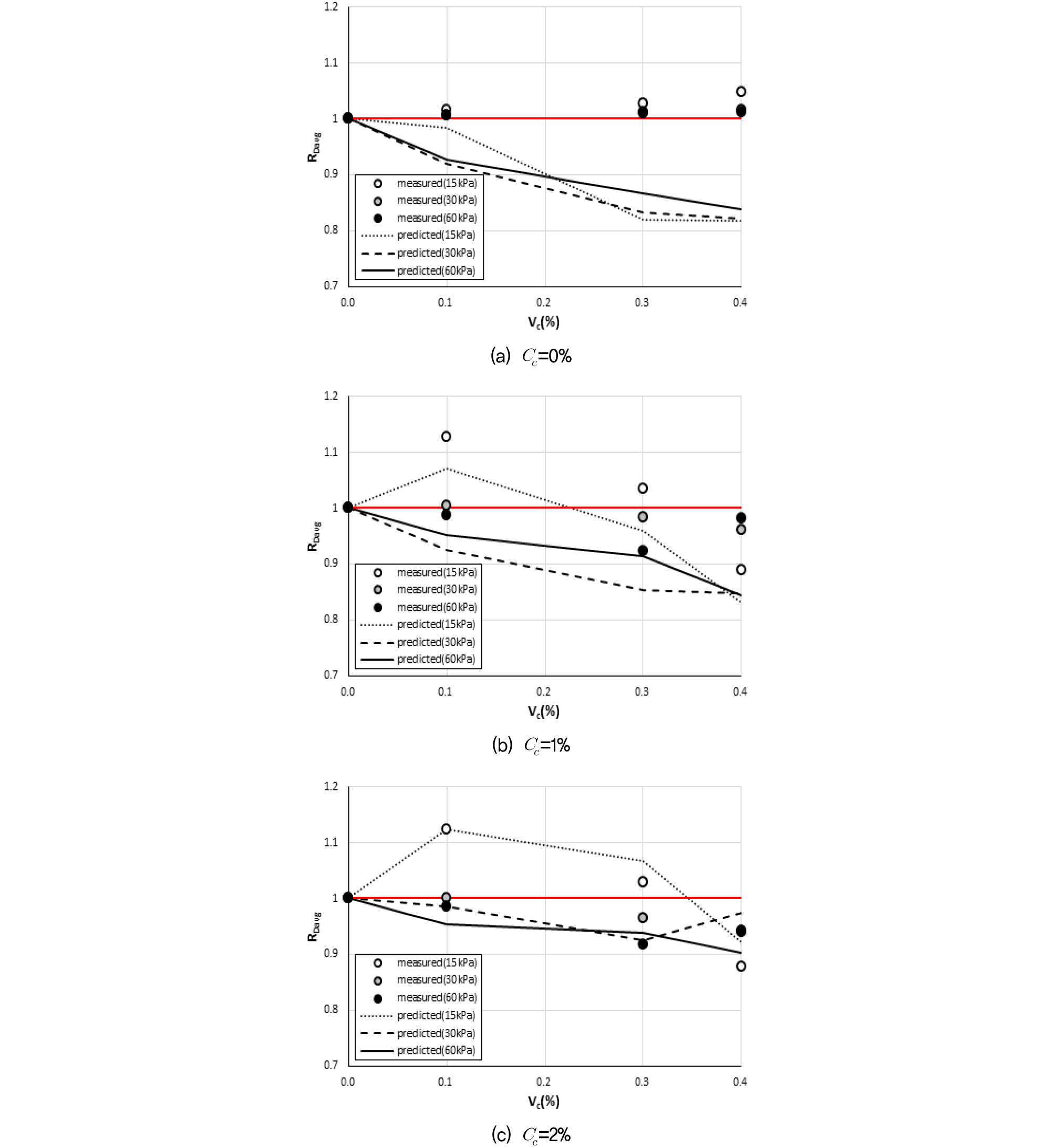
비닐스트립이 감쇠비에 미치는 영향을 살펴보기 위해 동일한 시멘트 혼합비 조건에서 비닐스트립이 없는 경우에 대한 있는 경우의 감쇠비 평균변화비, RDavg()과 비닐스트립 혼합비의 관계를 구속압 및 시멘트 혼합비에 따라 측정값과 제안식 산정값으로부터 계산된 RDavg값을 비교하여 Fig. 9에 도시하였다.
3.2절의 RGavg에서와 같이 비닐스트립에 의한 감쇠비의 변화가 본 연구의 산정식에 반영되는 평균적인 양상을 살펴보기 위해 공진주시험의 전단변형률 범위(0.0001~0.1%) 내 감쇠비의 평균값을 이용하였다. 비닐스트립에 의한 전단탄성계수의 증가는 감쇠비의 감소로 나타나는 것이 일반적이며, Fig. 9에서 보듯이 산정식에 의한 RDavg의 값은 1 이하로 Vc 증가에 따른 감쇠비의 감소현상을 반영하고 있다. 그러나 시멘트가 함유된 시편이 15kPa의 구속압을 받는 경우 Vc=0%~0.1% 구간에서는 RDavg가 증가하는데, 이는 낮은 구속압에 의한 감쇠비 증가경향이 비닐스트립에 의한 감쇠비 감소경향 보다 크게 발현되어 발생하는 현상으로 판단된다. 이러한 현상은 Cc가 증가할수록 더 뚜렷해지는데 전술한 시멘트에 의한 감쇠비 증가효과에 기인하는 것으로 판단된다. 또한 비닐스트립만으로 보강된 시편(Cc=0%)의 경우, 측정값에 의한 RDavg은 Vc의 증가와 함께 미세하게 증가하는 경향을 보일 뿐 만 아니라 1 이상으로 비닐스트립이 평균감쇠비를 증가시키는 것으로 측정되어 산정값에 의한 RDavg와는 반대의 경향을 보인다. 이는 시멘트가 없는 경우, 산정식에는 반영되지 않는 비닐스트립의 꼬임, 접힘, 혹은 구겨김 현상의 발생으로 인한 내부에너지 소산의 증가에서 기인하는 것으로 판단된다. 스트립 혹은 단섬유와 같은 단보강재가 지반 감쇠비에 미치는 영향에 대한 기존 연구결과를 살펴보면 전단탄성계수와는 달리 통일된 경향성이 없으며 감쇠비에 미치는 영향이 없다는 연구(Zhao et al., 2021)도 있어, 지속적인 연구가 필요한 것으로 사료된다.
5. 결 론
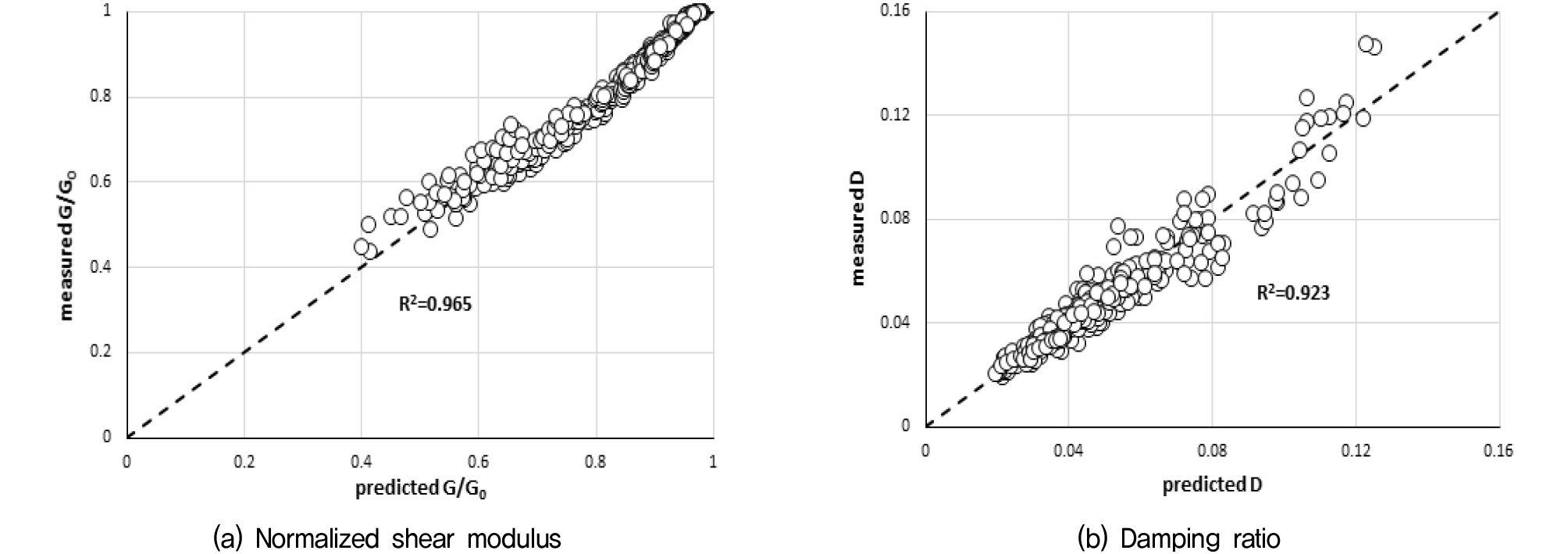
(1) 비닐스트립-시멘트로 보강된 느슨한 모래시편(상대밀도 40%)에 대한 공진주시험 결과를 이용하여 정규화 전단탄성계수 감소곡선과 감쇠비 곡선의 산정식을 제안하였다. 제안된 산정식은 보강조건(비닐스트립 및 시멘트 혼합비)과 구속압조건의 함수이며, 비닐스트립 혼합비 0~0.4%, 시멘트 혼합비 0~2%, 구속압 60kPa 이하의 범위에서 결정계수 0.9 이상의 높은 신뢰도를 보여주었다. 정규화 전단탄성계수 산정식과 감쇠비 산정식의 측정값과 산정값의 관계는 아래의 Fig. 10과 같다.
(2) 본 연구에서 제안한 정규화 전단탄성계수 산정식은 비닐스트립 및 시멘트 혼합비 증가에 따른 전단탄성계수의 증가현상과 시멘트 혼합비가 높은 경우 정규화 전단탄성계수에 대한 비닐스트립의 영향 감소현상을 잘 반영하고 있다. 또한 최대전단탄성계수 추정식을 제안하여 보강조건 및 구속압조건에 따른 전단탄성계수-변형률 관계곡선을 손쉽게 산정할 수 있게 되었다.
(3) 본 연구에서 제안한 감쇠비 산정식은 구속압 및 비닐스트립 혼합비 증가에 따른 감쇠비 감소현상과 시멘트 혼합비 증가에 따른 감쇠비 증가현상을 잘 반영하고 있으며, 시멘트 혼합비가 높은 경우 감쇠현상에 대한 비닐스트립의 영향이 뚜렷해지는 것을 보여주고 있다. 또한 제안된 감쇠비 산정식은 비닐스트립과 흙입자 사이의 활동 발생 전후의 감쇠비 변화에 비닐스트립 혼합비가 미치는 영향도 고려하고 있다.
(4) 본 연구에서 제안된 산정식을 이용하면 공진주시험을 수행하지 않고도 비닐스트립-시멘트로 보강된 느슨한 중간 모래지반의 정규화 전단탄성계수 감소곡선과 감쇠비 곡선을 간단히 추정할 수 있어 시험에 요구되는 비용과 시간을 절감하는 효과를 볼 수 있을 것으로 기대된다. 또한 제안한 산정식을 이용하여 비닐스트립-시멘트 보강 지반의 지반응답해석, 내진안정해석, 지반-구조물 동적상호작용 분석 등 실무적용성을 제고할 수 있는 추후 연구가 필요하다.