1. 서 론
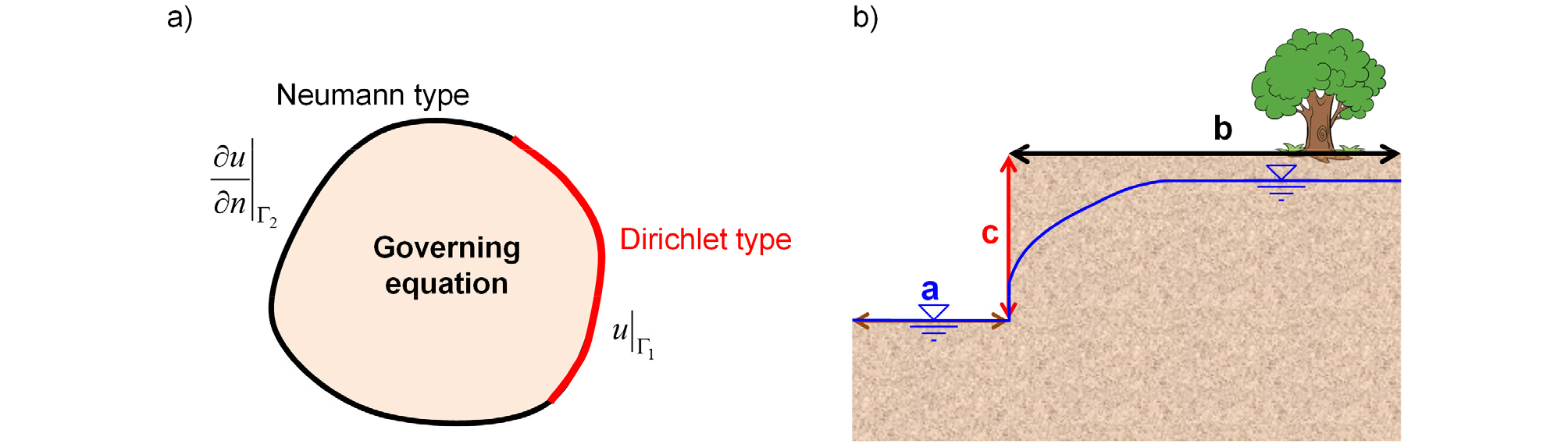
지반의 열-수리-역학적 현상에 대한 지배 방정식은 경계 조건(boundary condition)에 의하여 해석영역 내부의 변수값이 결정되는 경계값 문제(boundary value problem)이다(Table 1; Shin, 2011). 수치해석 프로그램을 이용하여 경계값 문제의 해를 구하기 위해서는 모든 경계를 Dirichlet 혹은 Neumann 형태로 지정해야 한다(Fig. 1a). Dirichlet 경계조건은 구성모델의 주변수(main variable)의 값을 직접 지정하고, Neumann 경계조건는 경계면의 법선방향으로 주변수의 공간적 기울기를 지정한다. 사용자가 지정하지 않은 경계조건은 Neumann 경계조건의 값이 0으로 자동 지정된다. 다만, 해석하고자 문제가 두가지 형태의 경계조건에 적합하지 않으면 이들을 조합한 Cauchy 형태의 경계조건을 이용하기도 한다.
Table 1.
THM problems and boundary conditions for geo-materials
| Simplified governing equation | Constitutive model | Dirichlet type | Neumann type | |
| Force equilibrium | ||||
| Water mass balance | P | |||
| Energy balance | T |
수치해석에서 역학적 문제에 대한 경계조건은 지정이 용이하지만, 수리적 문제에 대한 경계는 Table 1에서 제시된 2가지 형태로 지정하기 어려울수도 있다. 예로, Fig. 2b에서 가시설 지반굴착에 의한 바닥면(“a”)은 유입되는 지하수를 지속적으로 펌핑하면 Dirichlet 형태로 지정하고(P=0), 지면(“b”)은 강우나 증발을 무시하고 Neumann 형태로 지정할수 있다 (vn=0). 하지만, 연직 굴착면(“c”)은 간극수압이나 유량이 일정하지 않기 때문에 Dirichlet나 Neumann 혹은 조합으로 경계조건을 지정할수 없다. 수리학적 유출 경계조건은 식 (1) 같은 새로운 형태의 경계 모델이 필요하며, 대기에 노출된 지하수 흐름이나 Lysimeter와 1차원 강우 침투실험 등과 같은 모형실험에서도 필수적이다(Groh et al., 2016; Kim et al., 2012).
여기서 Rwd는 무차원의 물의 유출 저항계수(water discharge resistance)이고, <P>=max(P,0)을 의미한다. qex는 대기중으로 유출 유량이며, γw과 k는 물의 단위중량, 유출 경계에서의 불포화 투수계수이다.
지중온도는 지구내부 열원으로부터 지속적인 열흐름에 의하여 일정한 지열경사를 유지하며 연중 온도가 대체로 일정하다. 특히 깊이가 깊어질수록 높은 열용량으로 지표면의 온도변화에 의한 영향이 감소한다. 따라서 대부분의 열해석에서 관심영역이 지면으로부터 상당히 이격되어 있으면, 지면의 온도 혹은 대류열전달계수(Convective heat transfer coefficient)가 일정하다는 경계조건을 사용할 수 있다. 하지만, 지면의 온도 변화를 이용하는 지중탐사나 도시 열섬 현상에 대한 연구에서는 지면과 대기의 열적 상호작용, 그리고 지반의 열적-수리적 물성치의 영향을 고려해야 한다(Chen et al., 2019; Hwang, 2017; Qin and Hiller, 2014; Tan and Fwa, 1992).
본 연구는 지표면의 온도변화를 예측하기 위한 지반과 대기의 상호작용을 고려하는 열-수리적 경계조건에 대하여 논의하고자 한다.
2. 지면의 열적-수리적 경계조건
2.1 지면의 열적 에너지 평형
지면에서의 에너지 평형은 Fig. 2a와 같이 지면에 도달하는 태양복사(단파, qns), 지면으로부터 방출되는 지구복사(장파, qnl), 바람에 의한 대류(qc), 수분 증발에 대한 잠열(qe) 그리고 지중으로의 열전도 열전달량(ic|z=0)으로 표현할 수 있으며(Sedighi et al., 2018), 이를 수식으로 나타내면 식 (2)와 같다.
지면에 도달하는 단파 복사는 주로 태양 복사에너지이며, 순태양 복사 열유속은 다음과 같이 표현할수 있다.
여기서 는 지면의 알베도(albedo)로 대기중으로 반사되는 태양 복사의 백분율이다. qsolar는 태양 복사 강도이며 구름양(cloud cover)에 의존한다(Chen et al., 2019).
지면과 대기 중에서 방출되는 열 복사의 파장은 태양 복사의 파장보다 훨씬 길어서 장파 복사라고 한다. 지면과 천공 사이의 순장파 복사 열유속은 스테판-볼츠만(Stefan-Boltzmann) 법칙으로부터 식 (4)와 같이 산정할수 있다.
여기서 ε은 지면의 방사율(surface emissivity)이며, σ는 스테판-볼츠만 상수, 5.67×10-8W/(m2×K4)이다. Ts는 지면의 온도[K]이며, Tsky는 천공의 온도[K]이다(Fig. 2b). ψsky(sky view factor)는 천공의 관측 정도를 나타낸다(Gui et al., 2007).
바람에 의한 대기와 지면 사이의 대류현상은 식 (5)와 같이 표현할수 있다.
여기서 hc는 대류 열전달계수 [W/(m2×K)]이며 바람의 속도에 의하여 결정된다(Chen et al., 2019). 그리고 Ta는 대기온도를 나타낸다(Fig. 2b).
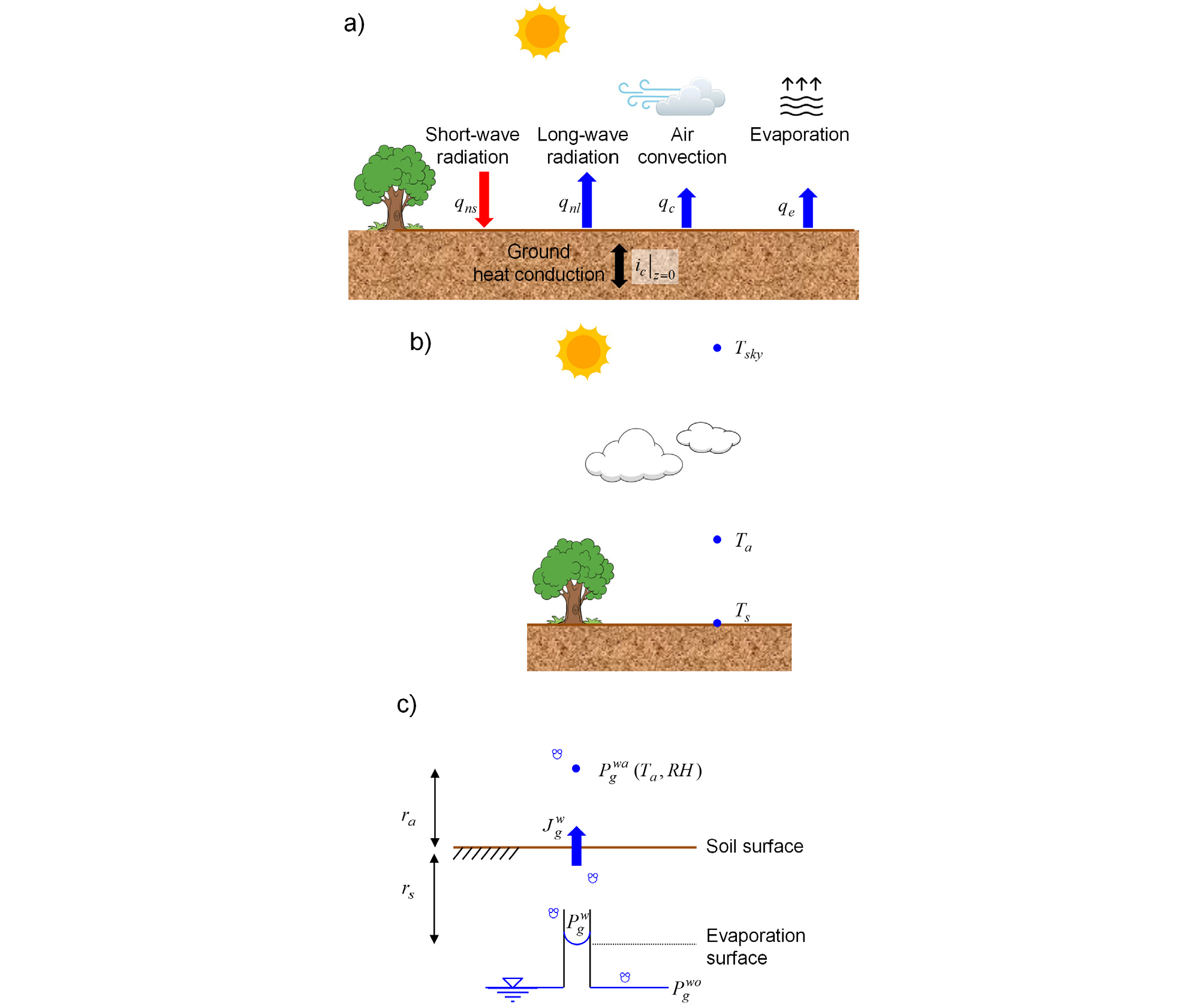
Fig. 2
a) Heat transfer process in soil-atmosphere interaction (Gui et al., 2017). b) Locations of temperature measurement. c) Schematic diagram for evaporation process (updated from van de Griend and Owe, 1994)
2.2 지면의 수분 증발
지면으로부터 수분 증발량을 산정하는 방법은 mass transfer 모델(Gray, 1970)과 resistances 모델(Aluwihare and Watanabe, 2003)로 구분할수 있다.
여기서 β는 지면 위의 풍속으로 결정되는 경험적인 계수이며, 대기중의 수증기압 Pgwa = RH·Pgws(Ta)은 대기의 상대습도(RH)와 대기온도(Ta)로부터 산정할수 있다. ra는 지면과 대기 사이의 증발에 대한 공기역학적 저항(aerodynamic resistance)이며 풍속의 함수이다. 그리고 rs는 증발면(evaporation surface, Fig. 2c)과 지면 사이의 증발에 대한 지반 저항(soil resistance)으로 공극내 물의 체적함수비로 결정된다. 식 (2)에서 수분 증발에 의한 열유속은 물의 기화 잠재열(Lgw=334kJ/kg)로부터 qe = LgwJgw과 같이 산정할 수 있다.
식 (6)에서 지중 증발면에서의 수증기압(Pgw)은 Kelvin의 방정식으로부터 다음과 같이 산정된다.
여기서 Pc는 지반내 공극의 모관흡수력(capillary suction)이며, Pgws(T)는 온도에 따른 포화 수증기압이다.
제시된 지면의 열적 에너지 평형 방정식과 증발에 대한 수리학적 제안식은 경계적분 형태로 수식화하고, 불포화 지반의 열-수리-역학 해석을 위하여 개발된 Geo-COUS(Geo-COUpled Simulator) 다차원 유한요소 프로그램과 결합하였다(Shin, 2011).
3. 울산지역 지면 온도 예측
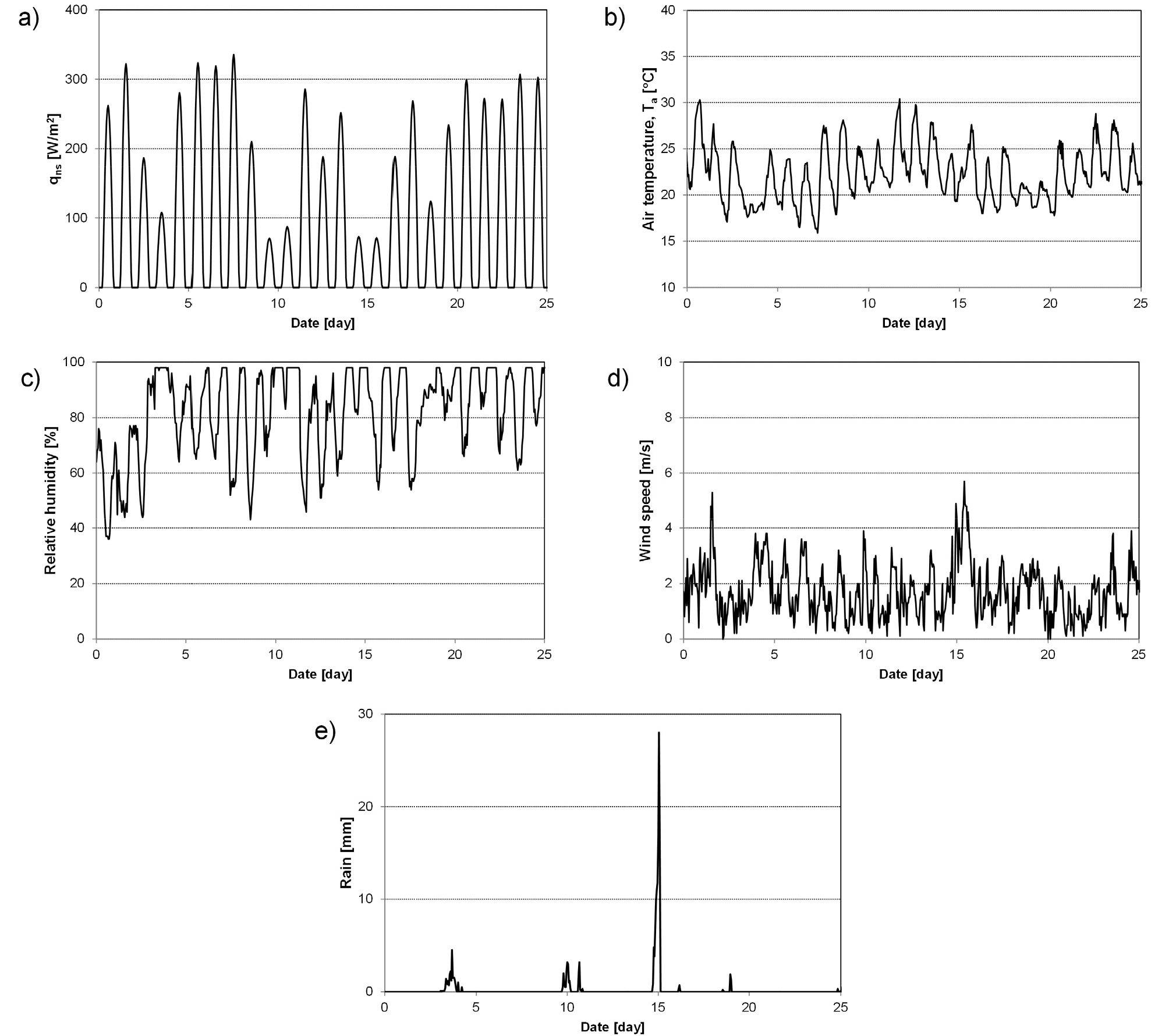
기상청에서 제공하는 2020년 6월15일~7월10일의 울산지역 기상데이터를 이용하여 지면 온도에 대한 수치해석을 수행하였다(KMA). 국내에서 태양하향복사는 안면도에서만 유일하게 관측되어 이를 이용하였다(Fig. 3a). Fig. 3b~3d는 해당기간 울산기상대에서 관측된 대기온도, 대기습도 그리고 풍속의 변화를 나타내고 있다. Fig. 3e는 울산기상대의 강우시기과 태양 복사에너지의 감소 기간이 일치하는 것을 보여주고 있다. Table 2는 수치해석에 사용한 지면의 조건에 따른 열적 물성치와 지중의 수리-열적 물성치를 정리하였으며, 아스팔트 포장해석에서 아스팔트의 두께는 20cm로 가정하였다.
Table 2.
Thermo-hydraulic properties for numerical simulations
|
Soil-atmosphere interaction |
Surface energy balance |
- Surface albedo [, -] 0.17 (bare soil), 0.12 (asphalt pavement) - Surface emissivity [ε, -] 0.972 (bare soil), 0.968 (asphalt pavement) - Solar radiation (qns, Fig. 3a) - Air temperature (Ta, Fig. 3b) - Air relative humidity (RH, Fig. 3c) - Wind velocity (u, Fig. 3d). |
| Evaporation model |
- Air temperature (Ta, Fig. 3b) - Air relative humidity (RH, Fig. 3c) - Wind velocity (u, Fig. 3d) - Resistance model aerodynamic resistance [s/m]: ra=505/u soil resistance [s/m]: rs = rs_min·exp[α(θmin-θ)] rs_min = 10.0, α = 0.3563, θmin = 0.20 | |
| Sub-surface | Hydraulic model |
- Soil-water characteristic curve Bare soil: , a=6kPa, b=5.0, c=0.5 Asphalt pavement: P0=0.2kPa, λ=0.1 (Yu-Shan and Shakiba 2021) - Saturated hydraulic conductivity [m/s] 1.0×10-5 (bare soil), 1.157×10-9 (asphalt pavement) - Relative hydraulic conductivity Bare soil: , λl=0.6 Asphalt pavement: krl = Sen, n=3.0 |
| Thermal model |
- Heat capacity [J/kg·K] 874.0 (bare soil), 920.0 (asphalt pavement, Zhao et al., 2020) - Thermal conductivity [W/m·K] λsoil=3.0, λwater=0.598 (bare soil), 1.2 (asphalt pavement, Zhao et al., 2020) |
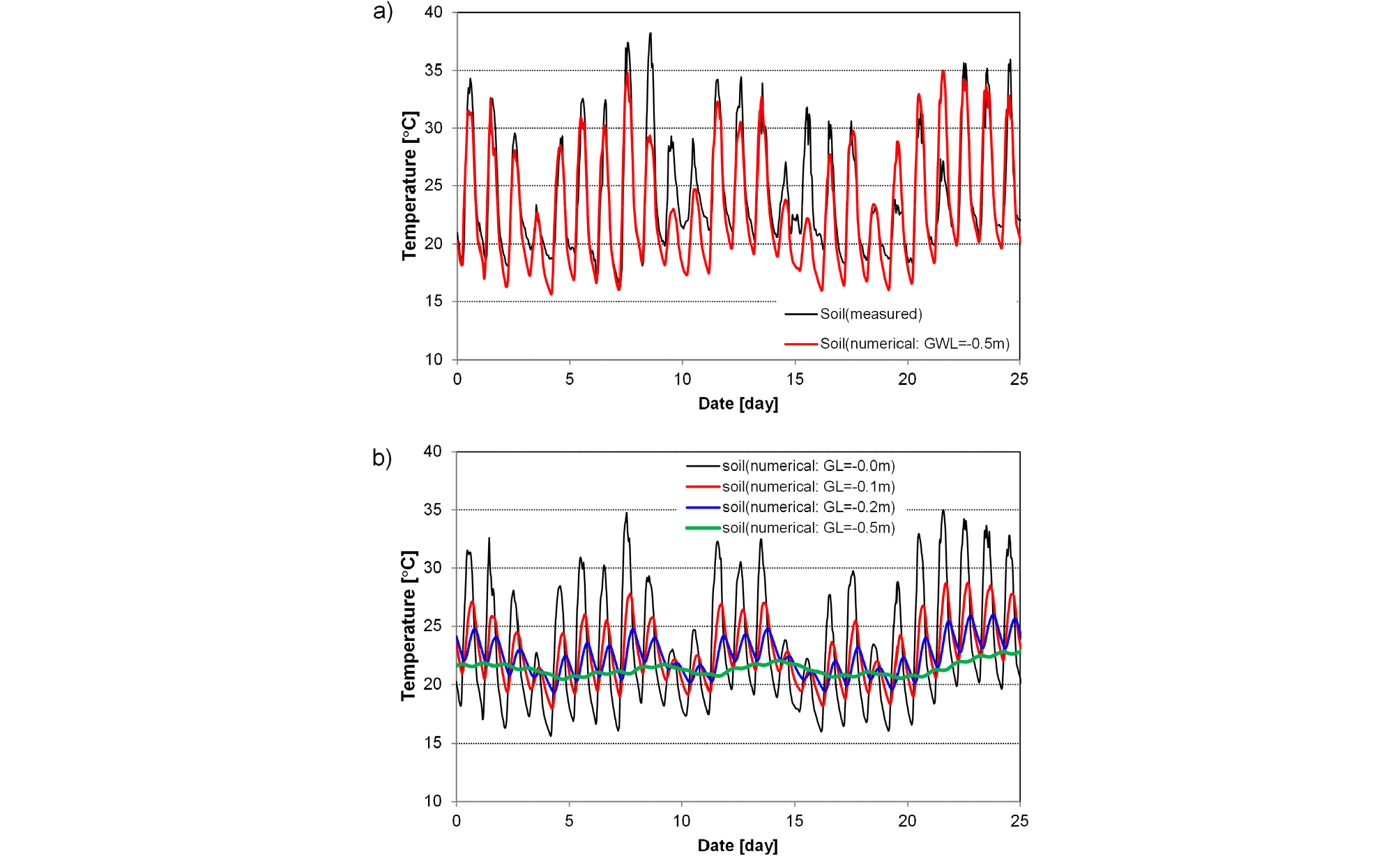
울산기상대에서 실측된 지표면 온도와 수치해석 결과는 유사한 경향을 보이고 있다(Fig. 4a). 다만, 수치해석은 강우와 지면의 열적 상호작용에 의한 지구복사에너지 차단 효과을 고려하지 못하여 지면 온도를 실측치보다 작게 예측하였다. 강우에 의한 대기중 열전달에 대하여 추가적인 연구가 필요하다(Chen et al., 2019).
Fig. 4b는 토사지반의 지하수위가 GWL=-0.5m인 조건에서 깊이에 따른 온도변화를 보여주고 있다. 지면과 대기의 열적 상호작용에 의한 온도변화는 깊어질수록 열확산으로 감소하고, 일최고와 최저온도가 발생하는 시점이 지연되었다. 그리고 지하수위 아래에서는 지반의 열용량의 증가로 지면의 영향이 더욱 크게 감소하였다.
Fig. 5a는 아스팔트 포장과 토사 지면조건에 대한 지면의 온도변화를 보여주고 있다. 낮시간에 아스팔트 포장은 토사 지반보다 약 10°C 높지만, 야간시간에는 온도 차이가 작게 나타났다. 토사지반에서 수분 증발에 사용되는 물의 기화 잠재열이 지면 온도를 낮추는 효과가 있다(Fig. 5b; Asaeda, 1993; Yilmaz et al., 2008). 그리고 야간시간에는 태양복사에너지와 수분의 증발이 사라지고, 대기와 지면의 열적 평형상태에 도달하면서 지면조건의 영향이 크게 감소하였다(Fig. 3b & Fig. 4a의 계측자료).
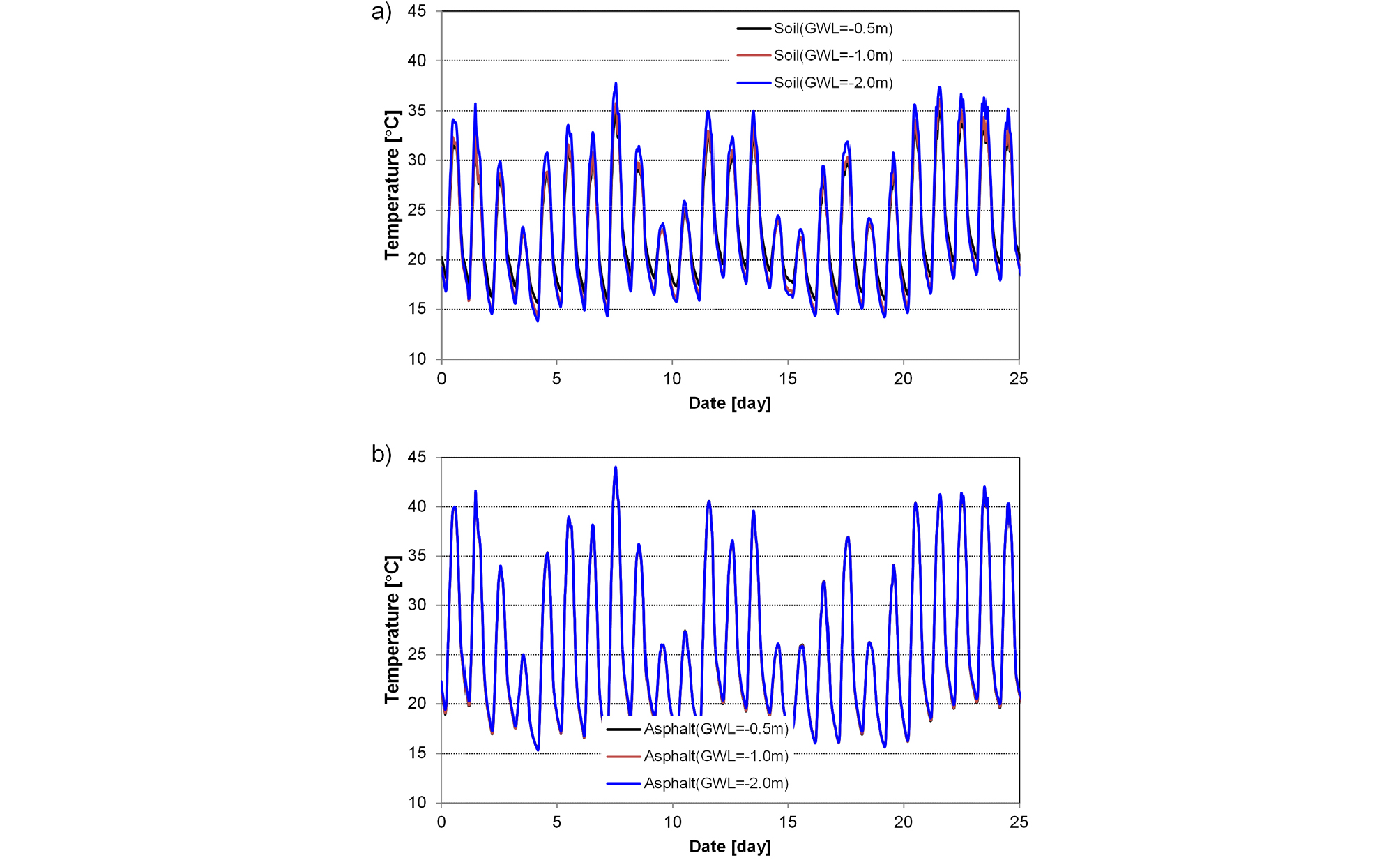
Fig. 6a는 토사 지면조건에서 지하수위에 따른 지면 온도변화를 나타내고 있다. 지하수위가 낮아질수록 지면의 모관흡수력이 증가하고 이로 인하여 수증기압이 감소한다(식 (7)). 그리고 체적 함수비의 감소로 증발에 대한 지반저항(rs)이 증가하여 증발량이 감소한다(식 (6)). 따라서 지하수위의 하강은 지면에서 수분 증발을 감소시시키고 지면 온도를 상승시키게 된다. 하지만, 아스팔트 조건에서는 작은 공극비와 낮은 투수계수로 증발량이 억제되어 지하수위의 영향이 매우 미비하게 나타난다(Fig. 6b).
4. 결 론
지반의 열-수리 현상에 대한 수치해석에서 경계조건의 설정은 해석결과에 매우 중요하다. 본 연구에서는 기존의 단순화된 경계조건이 아닌 지반과 대기와의 상호작용을 고려한 열-수리적 경계조건을 이용하여 지표면과 지중의 온도변화에 대한 수치해석을 수행하였다.
지표면의 에너지 평형은 지표면에 도달하는 태양복사, 지표면에서 방출되는 지구복사, 바람에 의한 대류, 수분 증발에 대한 잠열 그리고 지중으로의 열전도에 의한 열전달량으로 이루어진다. 수분 증발량은 Kelvin 방정식에 의한 지중 증발면의 수증기압과 지면의 수분 증발 모델로부터 산정하였다. 그리고 지중 열전도 열량을 산정하기 위하여 불포화 지반의 열-수리 현상에 대한 유한요소 프로그램과 연계하였다. 울산기상대에서 관측된 기상데이터를 이용하여 지면과 지중의 온도변화에 대한 수리-열적 수치해석을 수행하였다.
(1) 지표면 온도에 대한 수치해석는 울산기상대의 실측결과와 매우 유사하였으며, 지중에서의 온도변화는 열확산에 의하여 깊어 질수록 감소하였다.
(2) 낮시간 토사지반 표면의 온도는 수분증발에 의한 기화 잠재열로 아스팔트 표면보다 낮았으며, 야간시간에는 지면조건의 영향이 감소한 열적평형 상태에 도달하였다.
(3) 토사지반 조건에서 지하수위의 하강은 지면에서 수분의 증발을 감소시켜 지면의 온도를 상승시키지만, 작은 공극비와 낮은 투수계수를 갖는 아스팔트에서는 지하수위의 영향이 미비하였다.
수치해석 결과에 대한 관심 영역이 지표면 경계나 지중의 열원으로부터 충분히 이격되어 있으면 기존의 단순화된 열적 경계조건을 사용할수 있다. 하지만, 매설관이나 저수지의 누수, 지중 매설물의 대한 열화상 탐사, 도시 열섬 현상 등과 같이 지표면의 온도변화가 주요 관심사인 경우에는 지반과 대기의 열-수리적 상호작용을 고려한 수치해석을 수행해야 한다.