1. 서 론
2. 데이터베이스와 학습 알고리즘
2.1 데이터베이스
2.2 랜덤 포레스트
3. 모델 학습 및 결과 분석
3.1 모델 학습
3.2 모델 성능 및 입력변수 중요도 분석
4. 결 론
1. 서 론
2014년 서울시 송파구 신천동 일대에서 발생된 대규모 지반함몰을 시작으로 도심지에서 빈번하게 발생하는 지반함몰에 대한 우려가 매우 높아졌다. 국토교통부가 발표한 최근 6년간(2015~2020년) 연도별 지반함몰 발생현황을 보면 2020년에 284건, 2019년 192건, 2018년 338건, 2017년 279건, 2016년 255건, 2015년 186건으로 나타났다. 지역별로는 경기도가 302건으로 가장 많았고, 강원도 199건, 서울 156건, 충북 149건, 광주 122건, 대전 102건이 뒤를 이었다. 이처럼 국내 도심지에서 지반함몰이 꾸준히 발생하고 있으며, 지반함몰 예방을 위해 지난 6년간 647억원의 정부 예산을 투입했지만 지반함몰을 미연에 방지하기 위한 기술적 해법은 아직 부족한 상황이다.
KIGRAM(2014)에 따르면 지반함몰은 석회암 지대에서 발생하는 자연적 지반함몰과 지중 매설물 손상 혹은 지하 굴착으로 인해 발생되는 인위적 지반함몰로 구분된다. 국내의 경우 상부 지층의 대부분이 화강풍화토로 구성되어 있어 인위적 지반함몰이 주로 발생한다. 도심지에서 발생되는 인위적 지반함몰은 주로 하수관 손상에 기인하는 것으로 알려져 있다(Kuwano et al., 2010; Yokota et al., 2012; Bae et al., 2016). 대한민국 국회 국토교통위원회 천준호 의원에 따르면 국내의 경우도 하수관 손상이 전체 지반함몰의 44.2%(서울시는 46.0%)를 유발했다고 조사되어 주요한 원인으로 지적되고 있다. 따라서, 국내 도심지에서 발생되는 지반함몰을 예측하고 피해를 미연에 방지하기 위해서는, 하수관 손상으로 인해 발생되는 지반함몰 현상에 대한 연구가 필수적이다.
하수관 손상으로 인한 토사유실, 그리고 이에 따른 공동형성 및 지반함몰 발생에 대한 실험적 연구가 많은 연구자들에 의해 수행된 바 있다(Kuwano et al., 2010; Guo et al., 2013; Sato and Kuwano, 2015; Mukunoki et al., 2009; Indiketiya et al., 2017). 대부분의 모형실험은 모래를 활용해 모형지반을 조성한 뒤, 하수관 손상부를 모사한 하부 구멍을 통해 물의 유입과 유출을 반복하는 방식으로 모형시험을 수행했다. 그 결과 지반의 입도분포가 좋을수록 지반함몰에 대한 저항 능력이 우수하고, 세립분이 적고 평균입경과 초기 함수비가 클수록 지반함몰의 가능성이 증가하는 것으로 나타났다(Guo et al., 2013; Indiketiya et al., 2017). 상술한 연구들에서 사용된 모래가 국내 하수관 매립토로 사용되는 실트질 사질토와 차이가 있다는 문제를 해결하기 위해서, Kwak et al.(2019, 2020)은 화강풍화토로 모형지반을 조성해 지반함몰 모사시험을 수행하였다. 실험 중 모형지반을 촬영하고 디지털 이미지 해석을 수행해 강우강도, 세립분 함량, 매립심도, 다짐도 등에 따른 지반함몰 발생 유무를 평가하였다. 이상의 실험적 연구는 하수관 매립토의 특성이 지반함몰에 미치는 영향을 정성적으로 규명했다는데 의미가 있지만, 매립토의 특성을 하나씩 변화시켜가며 수행된 단변수적 연구라는 한계가 있다. 지반함몰은 여러가지 영향 인자들이 복합적으로 작용하여 나타나는 결과이므로 다양한 변수의 상호작용을 고려할 수 있는 분석이 필요하다.
한편, 도심지 지반함몰을 선제적으로 예측하기 위한 방법으로 관내 진단기술(CCTV, 부식탐지, 내시경 카메라 등)과 관외 진단기술(누수탐지센서, 열화상카메라, Ground Penetration Radar(GPR) 등)이 개발되었다. 관내 진단기술은 주로 관로의 일부 혹은 전체를 굴착해 관의 손상 및 지하공동을 직접 확인하는 방법으로, 시간과 비용적인 측면에서 광범위한 지역을 대상으로 적용하기에는 한계가 있다(KICT, 2020). 관외 진단기술은 관의 손상 혹은 지하공동 형성 시 발생되는 특징(수분, 열에너지, 진동 등)을 외부에서 찾아내는 기술이다. 관내 진단기술에 비해 상대적으로 시간과 비용적인 측면에서 강점이 있으나 이 또한 광범위한 지역 전체에 적용하기엔 무리가 있으며, 오차가 크고 불탐 구간이 존재한다는 한계가 있다(Kim et al., 2015).
본 연구에서는 머신러닝 기법 중 랜덤 포레스트를 기반으로 지반함몰에 영향을 미치는 다양한 인자(하수관 정보)로부터 도심지 지반함몰 발생 여부를 예측할 수 있는 모델을 만들고자 하였다. 모델을 학습시키기 위해 서울시 전역의 하수관 정보와 지반함몰 발생 위치 정보를 수집 및 활용하였다. 랜덤 포레스트 모델의 하이퍼파라미터를 최적화하여 모델의 성능을 극대화하였으며, 지반함몰 발생에 영향을 미치는 인자들, 즉 모델에 사용된 하수관 정보들이 모델에 미치는 상대적 중요도를 평가하여 지하공동 탐사 계획 수립 및 하수관 정비 사업 계획 수립의 기초 자료로 활용될 수 있도록 하였다.
2. 데이터베이스와 학습 알고리즘
2.1 데이터베이스
서울시는 운영중인 374,612개의 하수관의 정보를 하수도관리 전산시스템을 통해 관리하고 있으며, 매년 유지관리·기능고도화 및 GIS 데이터베이스 정확도 개선 사업을 통해 지속적으로 업데이트 하고 있다. 본 연구에서는 해당 시스템의 2018년 데이터베이스로부터 지반함몰에 영향을 미칠 수 있는 하수관 정보를 추출하였다. 서울시 하수도관리 전산시스템은 각 하수관에 대해 약 50여 개의 속성 정보를 제공하고 있다. 그중 기존 연구(Kuwano et al., 2010; Guo et al., 2013; Sato and Kuwano, 2015; Mukunoki et al., 2009; Indiketiya et al., 2017; Kim et al., 2018; Kwak et al., 2020)를 참고하여 손상된 하수관으로 인한 토사 유실 및 지반 침하·함몰 메커니즘에 영향을 미칠 수 있는 것으로 판단되는 7개의 속성을 위험도 평가 모델의 입력변수(설명변수)로 선정하였다. 선정된 입력변수 중 연속적인 특성값을 갖는 것으로는 하수관 크기, 길이, 해발고도, 기울기, 매립심도, 사용년수가, 범주형의 특성값을 갖는 것으로는 재질이 있었다. 하수관 재질에는 흄관, 콘크리트관, 주름관, PE관, PVC관 등 30여가지가 있는데, 이 중 흄관이 87.0%, 콘크리트관이 8.5%, 주름관이 2.0%, 나머지는 모두 합해 2.6%를 차지했다. 이에 본 연구에서는 흄관, 콘크리트관, 주름관을 제외한 나머지 관종은 ‘기타(others)’의 특성값을 갖도록 분류하였다. 다음으로 결측치(NULL value) 또는 이상치(outlier)를 포함하는 하수관을 데이터세트에서 제거하였다. 하수관 설치연도가 1920년 이전인 것, 길이가 0.1m 이하 또는 200m 이상인 것, 반경이 0.1m 이하인 것, 매립심도가 음수인 것 등을 이상치를 포함한 하수관으로 간주하였다. 그 결과, 최종적으로 216,188개의 하수관이 데이터베이스에 남게 되었고, 이는 서울시 전체 하수관 374,612개의 57.7%에 해당한다. Table 1에 설명변수 중 연속적인 값을 가지는 변수들의 기본통계량을 정리하였다.
Table 1.
Basic statistics of continuous predictor variables
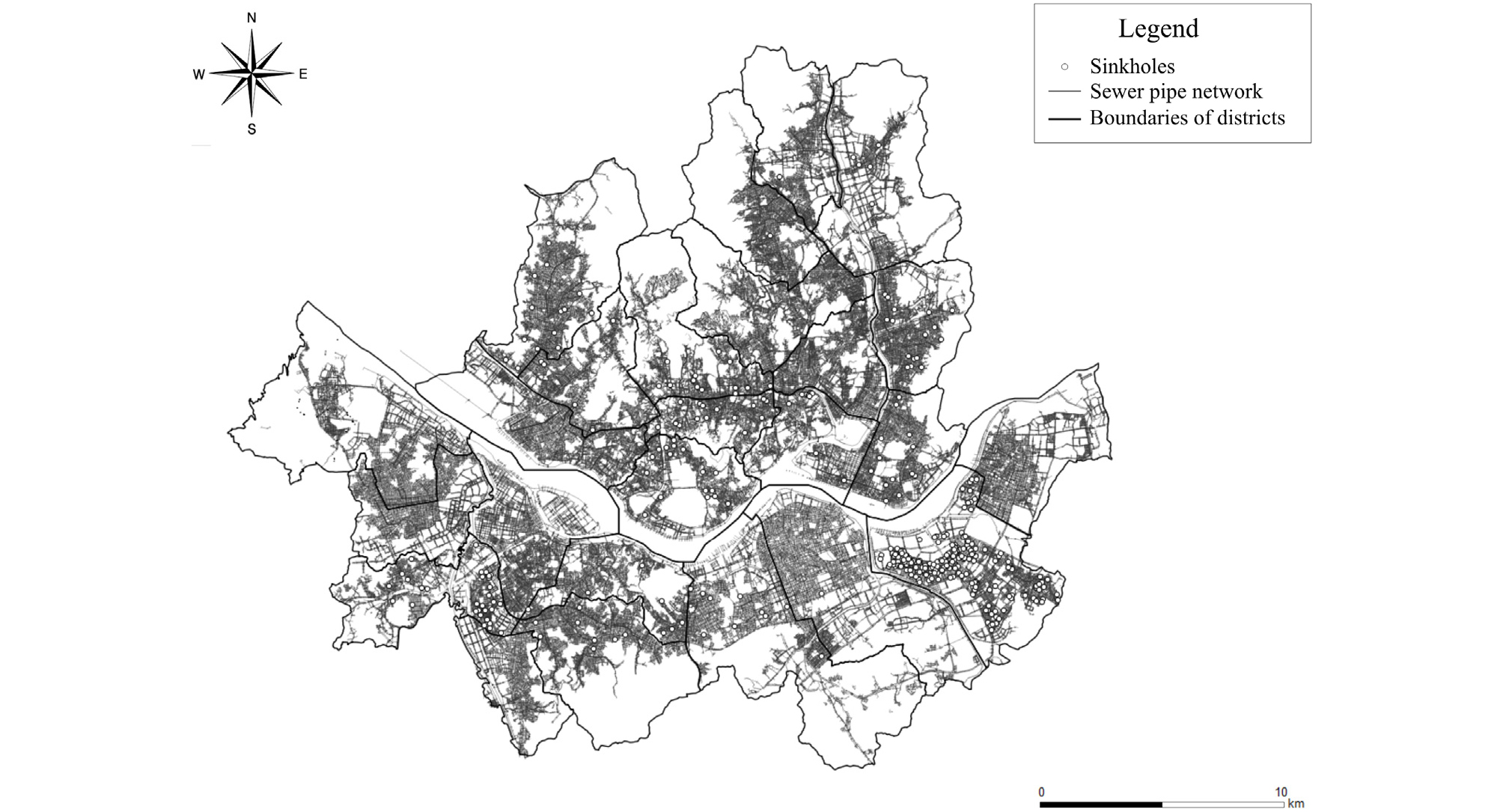
다음으로 어떤 하수관이 지반함몰을 유발하였는지 확인하기 위해, 2010년부터 2014년까지 약 5년간 서울시에서 하수관 손상으로 인해 발생한 1,100여 건의 지반함몰의 발생 위치 데이터를 확보하였다. Fig. 1에 서울시 하수관망도와 본 연구에서 취득한 지반함몰 발생 위치를 함께 도시하였다.
하수관의 특성값을 설명변수로, 지반함몰 발생, 미발생 여부를 반응변수(출력변수)로 하는 지반함몰 위험도 평가 모델을 도출하기 위해서는 지반함몰을 유발한 하수관을 특정할 필요가 있다. 하지만, 지반함몰이 도로상에 발생하는 경우가 많아, 이 경우 긴급한 복구가 필요하므로, 손상된 하수관에 대한 상세정보(관리번호, 손상 정도, 손상 부위)를 확인 및 기록하지 못한 경우가 대부분이었으며, 발생 위치 정보 또한 도로명 주소로 기록되어 있었다. 반면, 하수관의 위치정보는 TM(Transverse Mercator) 좌표계로 표현되어 있어, 하나의 좌표계로 통일하여 위치를 비교하기 위해 도로명 주소로 기록된 지반함몰 발생위치를 TM 좌표계로 변환하였다. 주어진 지반함몰 발생을 유발한 하수관을 특정하기 위해 GIS 소프트웨어를 이용하여 지반함몰 발생위치를 주변 하수관망도와 함께 도시한 다음 지반함몰 발생 위치와 가장 가까운 하수관을 해당 지반함몰을 발생시킨 하수관으로 가정하였다. 이 과정에서 지반함몰 발생 위치 주변에 하수관망이 복잡하여 하나의 하수관을 특정하기 어려운 경우, 해당 지반함몰 발생 케이스를 제외하였다. 하수관 특성값에 지반함몰 발생 유무를 표현하기 위하여 반응변수로서 ‘OCC’라는 속성을 추가하고, 지반함몰을 유발한 하수관으로 특정된 경우 이 속성값을 1로, 그렇지 않은 경우 0로 할당하였다. 이상의 과정을 수행한 결과, 데이터베이스 내 반응변수 OCC의 특성값이 1인 지반함몰을 유발한 하수관은 442개, OCC의 특성값이 0인 지반함몰을 유발시키지 않은 하수관은 215,746개로 나타났다.
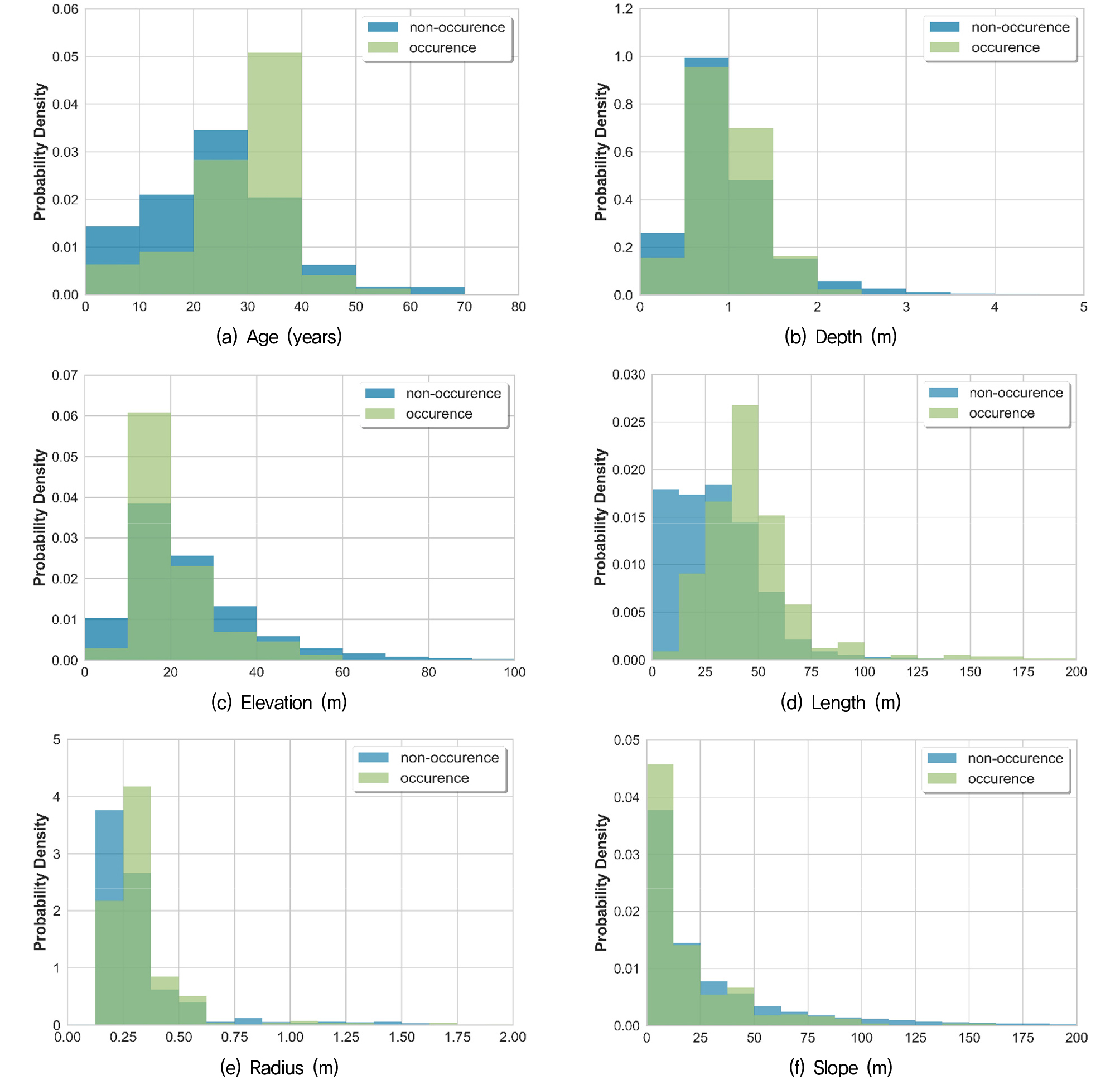
Fig. 2에 지반함몰을 발생시킨 하수관과 발생시키지 않은 하수관을 구분하여 본 연구에서 사용된 연속형 설명변수의 확률 밀도 함수를 나타내었다. 확률 밀도 함수의 비교를 통해 지반함몰을 유발한 하수관과 유발하지 않은 하수관이 각 변수별로 다소 상이한 확률분포를 가지고 있음을 정성적으로 알 수 있으며, 이 차이가 유의한지 통계 분석을 통해 확인할 수 있다. 하지만, 이러한 단일변수 분석은 각 변수가 지반함몰 발생에 영향을 미치는지 추론할 수 있으나, 지반함몰에 영향을 미치는 다양한 변수들을 함께 고려하였을 때 어떠한 변수가 더 큰 영향을 미치는지 확인하기 어렵다. 또한, 새로운 하수관 정보가 주어졌을 때 해당 하수관이 지반함몰을 유발할지, 유발하지 않을지 확률적으로 예측할 수 없다는 한계가 있다.
2.2 랜덤 포레스트
의사 결정 나무(decision tree)는 머신러닝의 지도 학습에 해당하는 알고리즘 중 하나로, 데이터를 분석하여 이들 사이에 존재하는 패턴을 예측 가능한 규칙들의 조합으로 나타내며, 귀납 추론을 위해 자주 사용되는 실용적인 방법이다. 데이터들을 트리 구조의 루트에서 시작하여 차례로 중간 노드(internal node)들을 거쳐 단말 노드(leaf node)에 배정하는 기능을 수행한다. 단말 노드의 지니 불순도(gini impurity) 또는 엔트로피(entropy)를 낮추는 방향으로 루트 노드 및 중간 노드에서 입력 변수 중 분류 기준(feature)과 기준값을 결정한다. 의사 결정 나무는 데이터를 가공할 필요가 거의 없고, 수치 자료와 범주 자료에 모두 적용할 수 있으며, 대규모의 데이터 세트에도 잘 작동한다. 결과를 해석하고 이해하기 쉽지만, 하나의 의사 결정 나무로는 복잡한 데이터로부터 반응 변수의 결과를 예측하는 데는 한계가 있다. 이에 따라 여러 개의 모델을 조화롭게 결합하여 모델의 예측 성능을 높이는 앙상블(ensemble) 방법의 기초 분류기(base learner)로 널리 활용된다. 랜덤 포레스트는 의사 결정 나무를 기초 분류기로 하여 랜덤하게 결정 나무의 숲을 만들고 각 결정 트리의 예측을 취합하여 최종 예측을 결정하는 대표적인 앙상블 기법이다.
랜덤 포레스트의 핵심은 여러 개의 학습 데이터를 생성하여 각 데이터마다 개별 의사 결정 나무 모델을 구축하는 배깅(bagging)과 의사 결정 나무 모델 구축 시 변수를 무작위로 선택하는 것(random subspace)에 있다. 배깅과 랜덤 부분공간의 사용은 의사 결정 나무들의 편향(bias)는 그대로 유지하면서, 분산(variance)를 감소시켜 랜덤 포레스트의 성능을 향상시킨다. 랜덤 포레스트는 의사 결정 나무의 쉽고 직관적인 장점을 그대로 가지고 있고, 데이터 전처리가 모델 학습에 미치는 영향이 상대적으로 적으면서 안정적이고 높은 성능을 보여 다양한 분야의 분류 및 회귀 문제에 널리 적용되고 있다. 최근 지반 공학 분야에서도 랜덤 포레스트 모델을 이용한 산사태 위험도 평가, 지반 강도 정수 예측 등의 연구가 다수 수행된 바 있다(Chen et al., 2017; Matin et al., 2018; Sun et al., 2021; Zhang et al., 2021). 본 연구에서도 이 랜덤 포레스트를 기반으로 지반함몰에 영향을 미치는 다양한 인자(하수관 정보)로부터 도심지 지반함몰 발생 여부를 예측할 수 있는 모델을 만들고자 하였다.
3. 모델 학습 및 결과 분석
3.1 모델 학습
랜덤 포레스트 모델을 학습시키기 위해 216,188개의 전체 하수관을 학습 데이터 세트(training set)과 테스트 데이터 세트(test set)로 분류하였다. 이때 학습 데이터 세트는 전체의 80%로 설정하였다. 본 연구에서 해결해야 하는 분류 문제는 지반함몰 발생 하수관이 전체 하수관의 0.2%밖에 되지 않는 균형이 맞지 않는 데이터(unbalanced data)를 활용한다. 지반함몰 발생 케이스가 적기 때문에 지반함몰을 유발한 하수관이 학습 데이터 세트 또는 테스트 세트에 집중하여 분포할 경우 모델 학습과 평가에 부정적인 영향을 끼치게 된다. 이러한 상황이 발생하지 않도록 전체 하수관에서 지반함몰을 유발한 하수관의 비율과 동일하게 지반함몰을 유발한 하수관이 학습 데이터 세트와 테스트 세트에 분포하도록 설정하였다.
랜덤 포레스트 모델은 다음 Table 2와 같은 대표적인 하이퍼파라미터(hyperparameter)를 가지고 있으며, 이 하이퍼파라미터들의 값에 따라 모델의 예측 성능이 크게 달라지므로 모델이 최고의 예측 성능을 갖도록 최적화하여야 한다. 최적의 하이퍼파라미터를 찾는 과정에서 학습 데이터 세트를 이용하여 모델을 학습한 후 고정된 테스트 데이터 세트를 이용하여 모델의 예측 성능을 평가하여 최적 모델을 도출할 경우, 해당 모델은 테스트 데이터 세트에 대해 특히 예측 성능이 높아지는데 이를 과적합(overfitting) 되었다고 한다. 과적합된 모델은 일반화 성능이 떨어져 새로운 데이터가 주어졌을 때 예측 성능이 떨어질 가능성이 높다.
Table 2.
Hyperparameters of random forest model
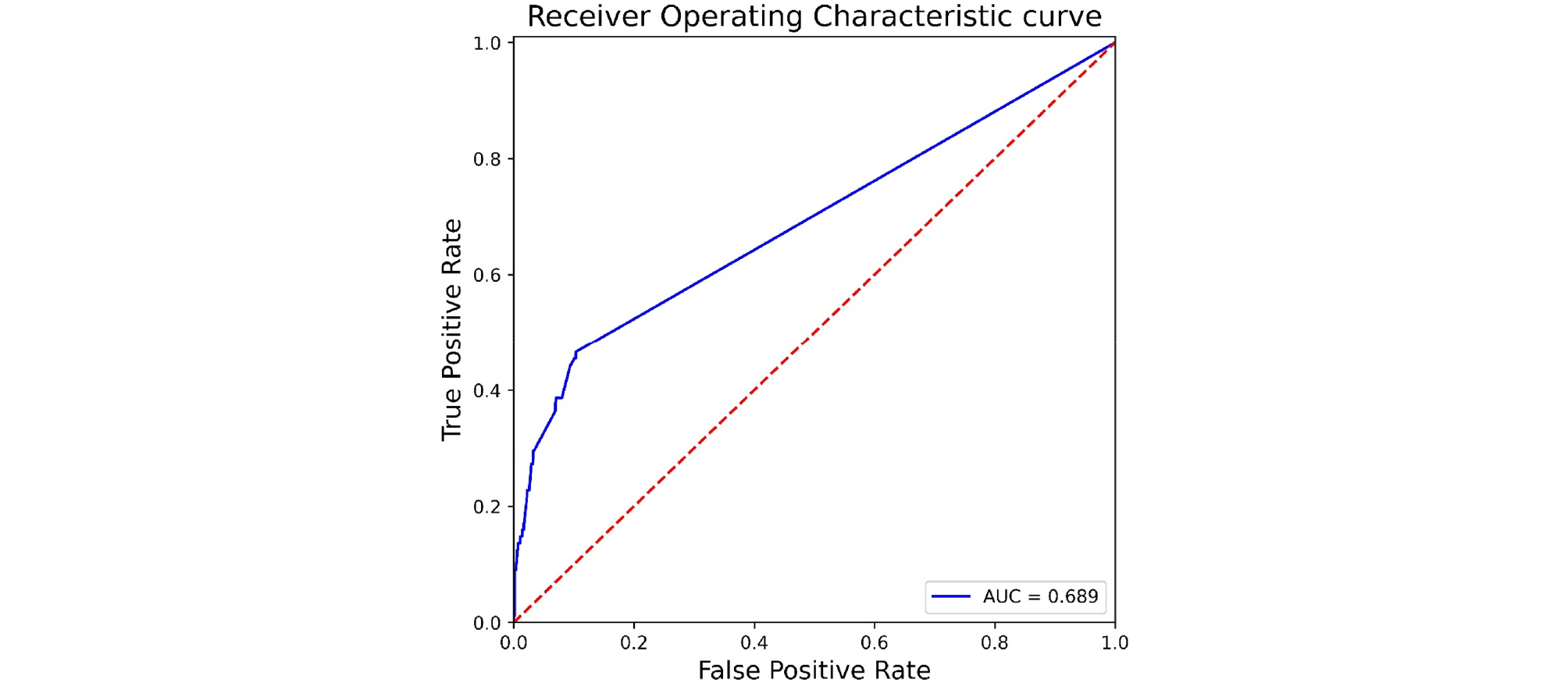
Scikit-learn(Pedregosa et al., 2011) 라이브러리 랜덤 포레스트 모델의 하이퍼파라미터 기본값(Table 2 참고)을 사용하여 랜덤 포레스트 모델을 학습한 후, 이를 테스트 데이터 세트에 적용한 ROC(receiver operating characteristic) 곡선을 Fig. 3에 도시하였다. ROC 곡선은 진단검사 결과에 근거하여 일련의 의사결정 기준점(decision threshold)에 대하여 가양성률(false positive rate)과 진양성률(true positive rate)을 나타낸 곡선이며, ROC 곡선의 하부 면적이 AUC(area under curve)로 정의된다. 이 AUC 값은 모델의 예측 성능을 평가하는 다양한 지표 중 하나로 본 연구에서는 AUC 값을 기준으로 하여 모델의 예측 성능을 평가하였다. Hosmer et al.(2000)은 AUC 값에 따른 모델의 예측 성능을 Table 3과 같이 제시하였다. Scikit-learn 라이브러리의 하이퍼파라미터 기본값으로 학습시킨 랜덤 포레스트 모델의 AUC 값은 0.689로 예측 성능이 좋지 않아 하이퍼파라미터를 최적화할 필요가 있음을 확인할 수 있다.
Table 3.
Area under curve and model performance
| AUC | Model performance |
| 0.9 - 1.0 | Outstanding |
| 0.8 - 0.9 | Excellent |
| 0.7 - 0.8 | Acceptable |
| 0.6 - 0.7 | Poor |
| 0.5 - 0.6 | No discriminatory ability |
3.2 모델 성능 및 입력변수 중요도 분석
하이퍼파라미터를 최적화하는 과정에서 과적합을 방지하기 위해 본 연구에서는 k-겹 교차 검증(k-fold cross validation) 방법을 이용하였다. k-겹 교차 검증은 테스트 데이터 세트를 모델 성능을 최종 평가하기 위해 떼어 두고, 학습 데이터 세트를 k개의 작은 세트들로 분할한 뒤, k-1개를 학습 데이터로 하여 모델을 학습시킨다. 모델 학습에 사용되지 않은 나머지 한 개의 데이터 세트를 마치 검증 데이터 세트(validation set)로 하여 모델의 성능을 평가한다. 이러한 과정을 k번 반복하여 얻은 성능의 평균치를 해당 모델의 성능으로 간주한다. 본 연구에서는 k값을 5로 하여 교차 검증을 수행하였다.
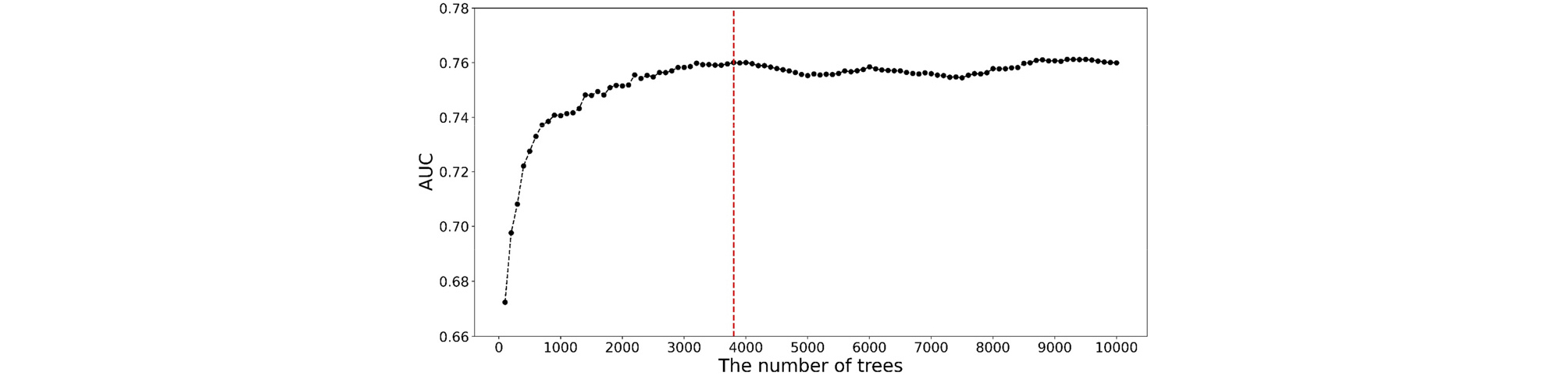
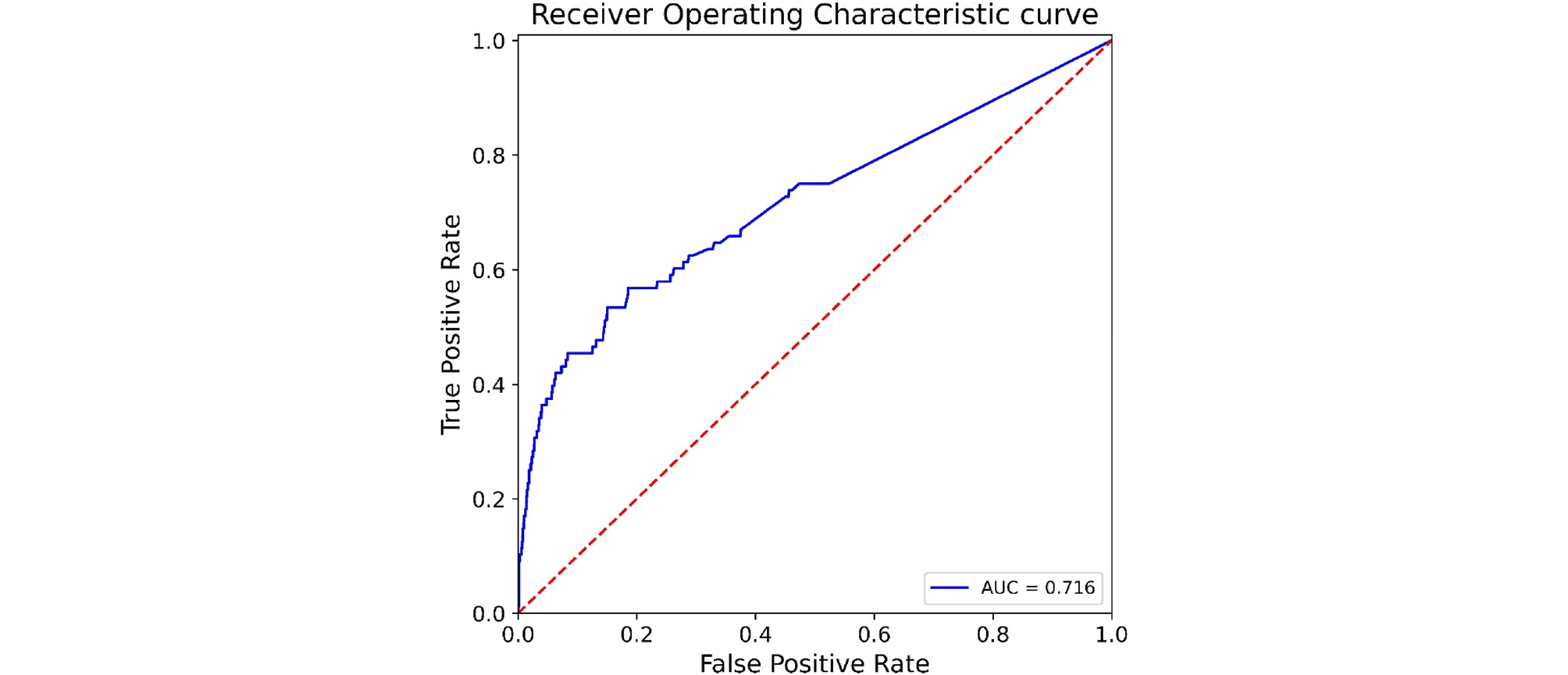
먼저 랜덤 포레스트 모델의 하이퍼파라미터 중 모델의 예측 성능에 가장 큰 영향을 미치는 의사 결정 나무의 수(n_estimator)를 최적화하였다. 교차 검증을 통해 의사 결정 나무 수를 100부터 10,000까지 100단위로 증가시키며 이에 따른 랜덤 포레스트 모델의 AUC 값 변화를 Fig. 4에 도시하였다. 랜덤 포레스트 모델은 일반적으로 의사 결정 나무 수가 증가할수록 성능이 향상되지만 계산량이 많아져 학습에 많은 시간이 소요되게 된다. 따라서, 의사 결정 나무 수가 증가함에 따라 모델 성능이 향상되는 이득이 적어지는 적정선에서 의사 결정 나무의 수를 정하는 것이 합리적이다. Fig. 4에서 의사 결정 나무의 수가 9,100일 때 AUC 값이 최대가 되는 것을 확인할 수 있으나, 의사 결정 나무의 수가 3,800일 때와 차이가 크지 않아 최적 의사 결정 나무의 수를 3,800으로 결정하였다. 의사 결정 나무의 수를 3,800으로 설정하여 학습시킨 랜덤 포레스트 모델을 테스트 데이터 세트에 적용한 ROC 곡선을 Fig. 5에 도시하였다. 이때 AUC 값은 0.716으로 하이퍼파라미터를 기본값으로 하였을 때보다 다소 향상되었으나, 학습 데이터 세트에서의 AUC 값에 비해 상당히 작게 나타나 추가적인 하이퍼파라미터 최적화가 필요함을 볼 수 있다.
본 연구에서 의사 결정 나무의 수 이외에 분할 시 고려할 기준의 최대 갯수(max_features), 분할의 질을 판단하는 기준(criterion), 의사 결정 나무의 최대 깊이(max_depth)를 모델 성능 향상을 위해 최적화하였다. 격자탐색(grid search) 방법을 이용하여 각 하이퍼파라미터가 가질 수 있는 값의 범주 또는 범위를 설정하고 모든 경우에 대해 교차 검증 시의 AUC 값을 비교평가하였다. 분할 시 고려할 기준의 최대 갯수는 3에서 7까지 다섯 가지 경우, 분할의 질을 판단하는 기준은 gini와 entropy 두 가지 경우, 결정 나무의 최대 깊이는 3에서 7까지 다섯 가지 경우를 고려하여 총 50 가지의 하이퍼파라미터 세트를 고려하여 최고의 모델 성능을 도출하는 하이퍼파라미터를 선정하였다. AUC 값을 기준으로 하였을 때, 상위 다섯 개 모델의 교차 검증 시 AUC 평균값과 그때의 하이퍼파라미터 값을 Table 4에 정리하였다. Max_features가 5, criterion이 entropy, max_depth가 7일 때 AUC 평균값이 0.8420으로 가장 높게 나타났다.
Table 4.
Summary of hyperparameter optimization
| Rank | max_features | criterion | max_depth | AUC |
| 1 | 5 | entropy | 7 | 0.8420 |
| 2 | 4 | entropy | 7 | 0.8419 |
| 3 | 3 | entropy | 7 | 0.8413 |
| 4 | 5 | entropy | 6 | 0.8406 |
| 5 | 6 | entropy | 7 | 0.8403 |
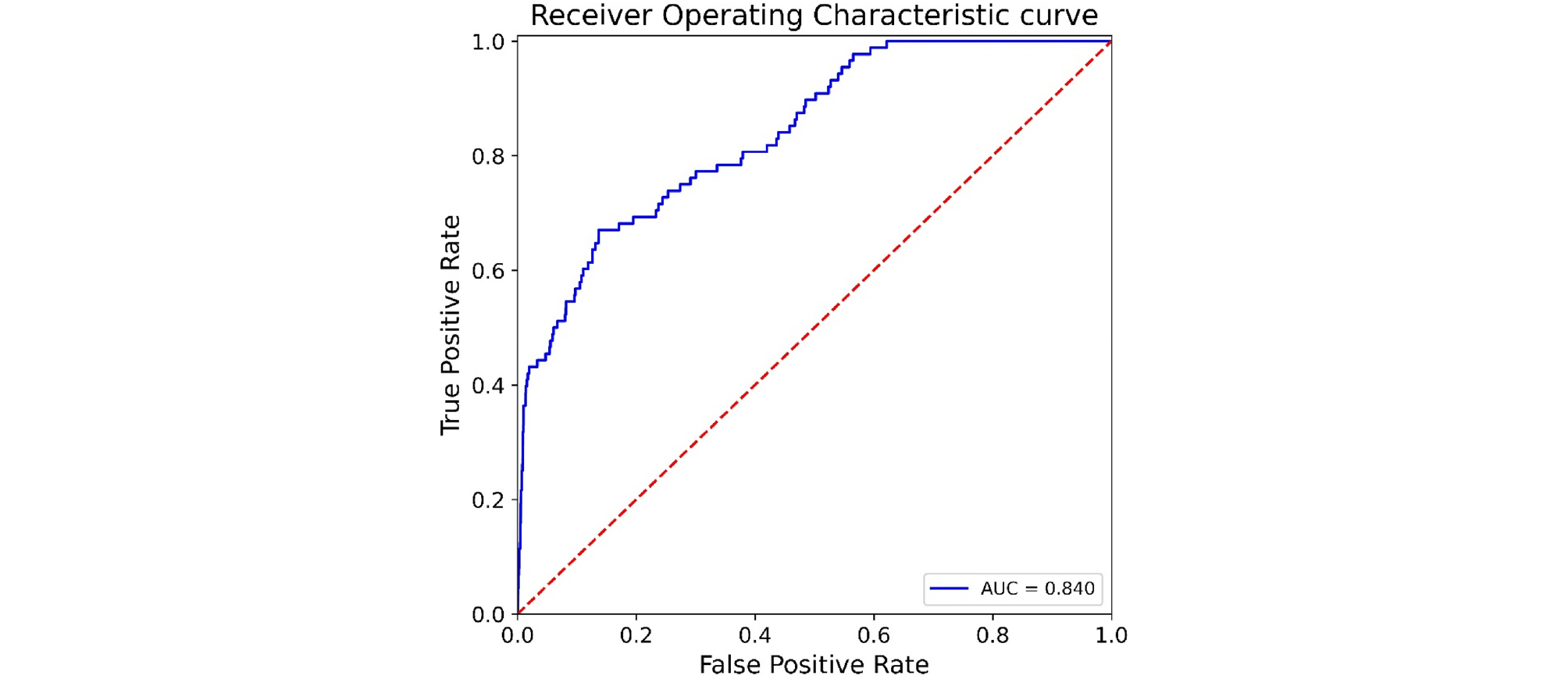
하이퍼파라미터 최적화 과정을 통해 획득한 최적값을 사용하여 랜덤 포레스트 모델을 학습하고 이를 테스트 데이터 세트에 적용한 ROC 곡선을 Fig. 6에 도시하였다. 그 결과 AUC 값이 0.840으로 테스트 데이터 세트에 대한 AUC 값 0.8420과 큰 차이가 없어 과적합이 발생하지 않았다. 하이퍼파라미터를 최적화한 랜덤 포레스트 모델의 예측 성능이 Hosmer et al.(2000)이 제시한 기준에 비춰볼 때 상당히 훌륭(excellent)하여(Table 3 참조), 이를 통해 도심지에서 하수관으로 인해 유발되는 지반함몰 발생 유무를 비교적 정확히 예측할 수 있음을 확인하였다.
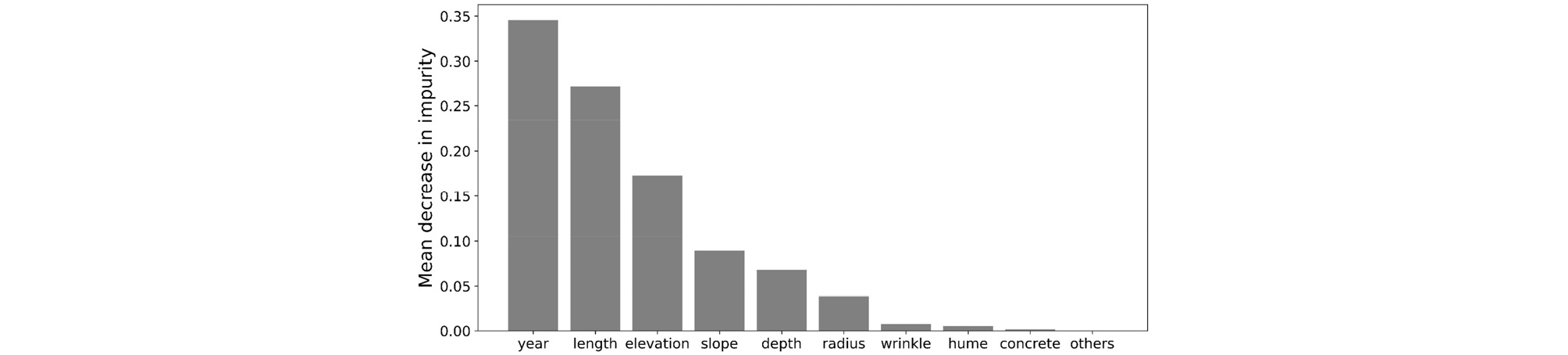
모델 입력변수의 상대적 중요성(feature importance)에 대한 정보를 얻을 수 있다는 것은 랜덤 포레스트 모델의 장점 중 하나이다. 본 연구에서는 불순도를 기반으로 입력변수의 상대적 중요성을 평가하여 Fig. 7에 정리하였다. 사용년수가 도출된 지반함몰 발생 예측 모델에 가장 큰 영향을 미치는 것으로 나타나 노후 하수관 정비의 필요성을 다시 한번 확인할 수 있었다. 사용년수 이외에는 길이, 해발고도, 경사, 매립심도, 하수관 크기의 순서로 입력변수의 상대적 중요도가 감소하는 것으로 나타났으며, 범주형 변수인 하수관 재질의 경우 하수관이 주름관일 때 가장 영향이 크지만 다른 입력변수에 비해서는 중요도가 크게 떨어지는 것으로 나타났다.
4. 결 론
본 연구에서는 머신러닝 기법 중 랜덤 포레스트를 기반으로 도심지 지반함몰 발생 여부를 예측할 수 있는 모델을 만들기 위해 서울시 전역의 하수관 정보와 지반함몰 발생 위치 정보를 수집하였다. 공간정보 분석을 통해 지반함몰을 발생시킨 하수관을 특정하여 반응 변수의 특성값이 1이 되도록 하고, 그렇지 않은 경우에는 0의 특성값을 부여하였다. 또한, 문헌 연구를 통해 많은 하수관 속성 정보 중 손상된 하수관으로 인한 지반함몰 유발에 영향을 미칠 것으로 예상되는 인자들을 선별하고, 이에 대해 결측치 및 이상치 필터링을 수행하여 최종적으로 관측값이 216,188개, 속성 정보가 10개인 데이터베이스를 구축하였다.
구축한 데이터베이스에 하이퍼파라미터 기본값을 갖는 랜덤 포레스트 알고리즘을 적용한 결과 모델 예측 성능이 매우 떨어지는 것을 확인하고, 격자탐색 방법을 이용하여 랜덤 포레스트 모델의 하이퍼파라미터를 최적화하였다. 그 결과, 테스트 데이터 세트에 대한 AUC 값이 0.840에 이르는 상당히 우수한(excellent) 예측 성능을 갖는 지반함몰 위험도 평가 모델을 도출하였다. 도출한 모델로부터 입력변수들의 상대적 중요성을 평가하여 사용년수, 길이, 해발고도, 경사의 순서로 지반함몰 발생 위험에 영향을 미치고 하수관 재질은 큰 영향이 없는 것을 확인하였다.
본 연구에서 도출한 랜덤 포레스트 모델의 지반함몰 발생 여부 예측 결과를 활용하여 지반함몰 위험도 지도의 작성이 가능하며, 이는 지하공동 탐색 등의 지반함몰 재해 관리 계획 수립과 노후 하수관 교체 등의 하수관 정비 사업 계획 수립에 유용한 자료로 활용될 수 있을 것으로 기대된다. 본 연구에서 하수관 관련 정보만을 이용하여 상당히 높은 성능을 가진 지반함몰 발생 예측 모델을 학습할 수 있음을 확인하였으나, 기존의 실험적 연구에서 지반 특성이 토사 유실 및 지반함몰 발생에 영향을 미치는 것을 확인하였으므로, 향후 연구에서 입력변수로 지반 정보를 추가 활용한다면 더 높은 성능의 예측 모델을 학습할 수 있을 것으로 판단된다.