1. 서 론
2. 해석 방법과 데이터 생성
2.1 유한요소법
2.2 한계평형해석법
2.3 사면 도메인의 구성
3. 다층 퍼셉트론 신경망과 모델 훈련
4. 결 과
4.1 사면의 안전율 예측
4.2 사면의 파괴 원호 예측과 Morgenstern-price 방법을 통한 정량적 평가
4.3 모델 입력 인자의 민감도 분석
5. 요약 및 결론
1. 서 론
한국은 지형의 3/4 가량이 산지로 되어 있기에 사면은 인공 사면과 자연 사면을 포함하여 널리 분포하는 구조물이다(National Geographic Information Institute, 2008). 사면의 붕괴는 대규모로 일어나는 경우가 많고 국내의 사면 붕괴와 그로 인한 피해 사례도 지속적으로 보고되기에 사면의 안정해석을 수행하는 것은 매우 중요한 지반공학적 문제이다(Singh et al., 2008; Wang et al., 2013; Bünz et al., 2005; Oh et al., 2008; Song, 2006). 그리하여 사면의 안정해석은 전통적인 절편법으로부터 시작하여 유한요소해석을 통한 강도감소법(Dawson et al., 1999; Matsui et al., 1992; Kim, 2004), 강우침투를 고려한 수치해석(Cai, 1998; Cai, 2004; Duong, 2019; Wei, 2019; Cho, 2019; Park and Ahn, 2019), 지하수를 고려한 지진에서의 사면안정해석(Lu, 2015) 등의 방법으로까지 발전하였다. 기존에 사용되던 유한요소법을 이용하는 방법의 경우 해석을 위한 도메인의 조건과 메쉬를 구성하는 데에 어려움이 있다는 단점이 존재한다.
그로 인해 최근 단순한 형태의 인공지능을 사면안정해석에 적용하여 보조적인 수단으로 이용하고자 하는 시도가 꾸준히 이루어지고 있다. 단순한 형태의 인공신경망(artificial neural network, ANN), 다중 회귀(multiple regression, MR), 유전적 알고리즘(genetic algorithm, GA), 서포트 벡터 머신(support vector machine, SVM)을 이용하여 지하수가 없는 사면의 안전율을 예측하는 내용이 보고되었다(Erzin and Cetin, 2013; Bui, 2020). 또한 로지스틱 회귀(logistic regression), 결정 트리(decision tree), 랜덤 포레스트(random forest, RF), 그라디언트 부스팅 머신(gradient bosting machine, GBM), SVM, 다층 퍼셉트론(multi-layer perceptron, MLP), 반딧불 알고리즘(firefly algorithm)을 이용하여 지하수가 존재하는 사면의 안정/불안정 여부를 판단하는 기계학습 알고리즘이 제시되었으며(Qi and Tang, 2018; Hoang and Pham, 2016), 더 나아가 지하수를 고려한 사면의 안전율을 예측하는 모델을 SVM, 에이다부스트(AdaBoost), GBM, RF, GA 등의 방법을 이용하여 훈련할 수 있음이 보고되었다(Samui, 2008; Shang et al., 2021; Lin et al., 2022). 최근 합성곱 신경망(convolutional neural network, CNN)을 활용하여 사면을 표현하는 입력인자를 0~255의 정수로 정규화하여 이미지로 입력을 표현하면 안전율을 예측하는 모델도 제시되었다(Azmoon et al., 2021). 또한 현장의 사면 형상을 모델링하고 획득한 물성으로 인공지능 모델을 훈련하여 해당 지역 사면의 파괴 여부를 예측하는 시도 역시 이루어지고 있다(Maxwell et al., 2020; Ghorbanzadeh et al., 2019; Ullo et al., 2021). 다만 많은 시도가 단순히 사면의 안전율을 예측하는 데에 그쳐 임계활동면에 대한 정보를 얻을 수 없거나 지하수위를 단순히 간극수압비로 고려하여 사면 내 지하수위의 분포와 불포화토의 모관흡수력에 대한 고려가 없다는 한계점이 존재한다.
사면의 파괴는 주로 지하수의 영향을 크게 받는 것으로 알려져 있지만(Brönnimann, 2011; Zhang et al., 2012) 사면에서 지하수는 불포화토에서 모관흡수력(matric suction)을 통해 전단강도를 증가시키기도 한다(Ng and Shi, 1998). 실제로 자연상태에서 대부분의 지반은 완전한 건조 상태나 포화 상태 보다는 불포화토로 존재하기 때문에 불포화토의 역학적 특성을 고려한 사면의 안정해석 결과는 현장 적용성이 높다.
따라서 본 연구에서는 간단한 형태의 인공지능인 MLP를 이용하여 사면안정해석을 수행할 수 있도록 훈련하였다. 안전율을 예측하기 위한 모델과 원호파괴면을 예측하기 위한 모델을 각각 훈련하였으며, 두 모델의 결과를 비교하기 위해 임계활동면을 예측하는 모델을 평가할 수 있는 방법론을 제시하여 단순히 안전율만 예측하는 모델에 비해 파괴 원호를 예측하는 경우 더 좋은 성능을 나타낼 수 있음을 입증하였다. 훈련에 사용된 사면의 모델링에서 지하수의 존재로 인한 불포화토의 모관흡수력을 고려하기 위해 건조 사면과 지하수위가 단계별로 고려된 사면의 경우를 모두 해석하여 데이터를 생성하였다.
2. 해석 방법과 데이터 생성
2.1 유한요소법
사면의 지하수 조건을 고려하기 위해 일반적으로 사용되는 유한요소법을 이용한 침투해석을 적용하였다. 수치해석에서는 구조를 사실상 유한한 크기의 요소로 나누고, 이러한 요소들의 집합체로 구조를 해석한다. 본 연구에서는 지하수의 정상상태 침투를 분석하기 위해 Geostudio 2012 소프트웨어의 SEEP/W 프로그램을 사용하였다. 분석하고자 하는 사면을 구성하는 토질은 국내 다양한 지역의 지반조사 결과를 참고하여 자연계에 널리 분포하는 세립분이 포함된 사질토를 가정하였다(Park et al., 2017; Jung et al., 2014). 체적 함수율 함수는 사면을 구성하는 토질이 가질 수 있는 체적함수율의 범위에서 모관흡수력을 최대 1,000kPa, 최소 0.01kPa를 가지도록 프로그램에서 계산하여 사용하였다. 이 체적 함수율 함수를 기반으로 수두(h)와 수리전도도(Kr(h))의 관계를 나타내는 수리전도도 함수를 van Ganuchten 방법으로 추정하였다(van Genuchten, 1980). 수리전도도 함수의 형태는 식 (1)로 표현되며, m, n, α는 van Genuchten 모델 파라미터이다.
2.2 한계평형해석법
사면의 안전율을 구하기 위해 한계평형해석법을 이용하여 사면안정해석을 수행하였다. 사면안정해석 방법은 크게 확률론적 해석방법과 결정론적 해석방법으로 구분되며, 결정론적 해석방법 중 한계평형법에 기초한 절편법이 널리 사용되고 있다. 극한평형법은 부정정 문제이기 때문에 문제를 풀기 위해서는 미지수에 비해 부족한 방정식의 수만큼 가정이 필요하다. 이 가정의 차이에 따라 일반 절편법, Bishop의 간편법, Janbu의 간편법, Morgenstern-Price법 등 여러 방법이 제안되었다(Bishop, 1955; Janbu, 1973; Morgenstern and Price, 1965).
본 연구에서는 Geostudio 2012 소프트웨어의 SLOPE/W 프로그램을 사용하여 절편 사이의 힘과 모멘트 평형을 모두 고려할 수 있는 Morgenstern-Price 방법을 통해 사면의 안전율과 임계면을 구하였다(Morgenstern and Price, 1965). 이 과정에서 지하수 조건은 SEEP/W의 해석결과를 사용하였으며, 불포화토의 유효응력에 대한 모관흡수력의 영향을 고려하여 해석하였다. 또한 지하수가 존재하지 않는 경우와의 비교를 위하여, 동일한 조건으로 건조 상태 사면에 대한 분석을 수행하였다.
2.3 사면 도메인의 구성
수치해석에 사용된 사면 형상은 6개 사면 높이 조건(H: 10, 12, 14, 16, 18, 20m)과 5개 비탈면 기울기 조건(β: 1:1.0, 1:1.2, 1:1.5, 1:1.8, 1:2.0)을 조합하여 구성하였다. 이 때, 비탈면 기울기는 지반설계기준의 비탈면 설계기준 중 쌓기·깎기의 표준경사를 참고하여 토질 특성이나 비탈면 조건에 따라 1:0.8 ~ 1:2.0의 범위에 분포하도록 하였다(Ministry of Land, Infrastructure and Transport, 2020). 지하수위가 존재하지 않는 건조 조건을 포함하여, 사면 내에 지하수위가 분포하는 경우를 고려하기 위해 각 사면 형상에서 지하수위의 높이를 사면 높이로 정규화한 값(Hw*: -1.0, 0, 0.2, 0.4, 0.6, 0.8, 1.0)으로 7개 지하수위 조건을 설정하였다. 해당 해석단면에 대해 지반조건을 설정하기 위해 세립분이 혼합된 사질토의 토질정수를 부여하였다. 한편, 흙의 단위중량은 마찰각과 점착력에 비해 사면의 안전율에 큰 영향을 미치지 않는 것으로 알려져 있다(Sakellariou and Ferentinou, 2005; Kim and Cho, 2006). 일반적인 세립분이 혼합된 사질토의 공극률은 0.145에서 0.495 사이에 분포하는 것으로 알려져 있으며, 이에 따라 고체의 비중(Gs)은 2.65로 간주하여 건조단위중량(γd)의 범위 13.0 ~ 22.35kN/m3로 설정하였고, 마찰각(ϕ) 및 점착력(c)은 제시된 범위에서 균일하게 분포하도록 설정하였다(Swiss Standard SN 670 010b, 1999)(Fig. 1).
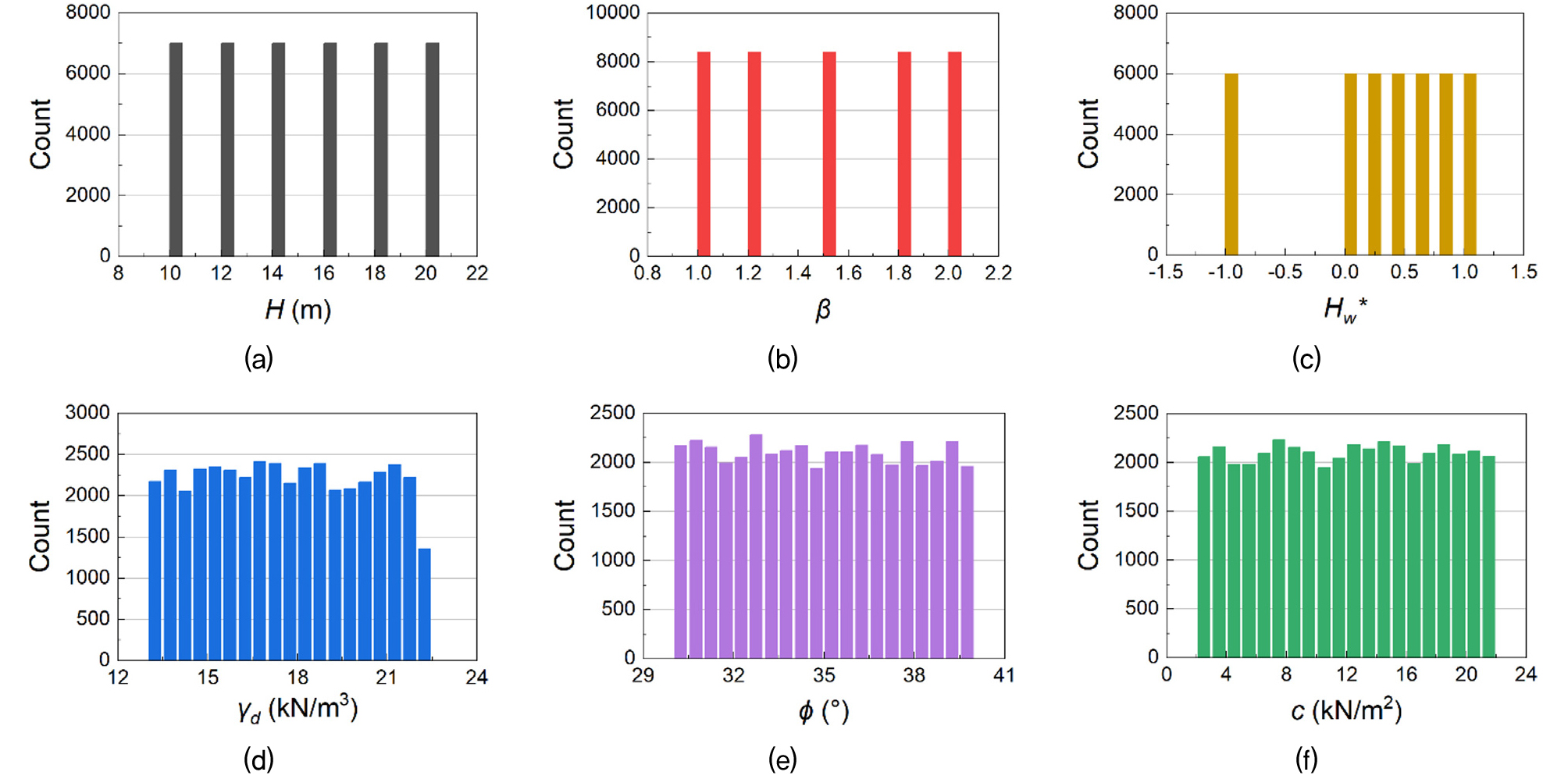
Fig. 1
Distribution of input parameters used to generate slope stability analysis data to be used for training the MLP model: (a) slope height (H), (b) cotangent of slope angle (β), (c) groundwater height normalized to slope height (Hw*) (d) dry unit weight of soil (γd), (e) friction angle of soil (ϕ), and (f) cohesion of soil (c)
30개 사면 형상과 건조단위중량, 마찰각, 점착력 등 200개 토질정수조건, 7개 지하수 조건을 조합하여 총 42,000개의 사면 해석 도메인을 준비하였다. Table 1은 42,000개 해석 도메인에 부여된 사면 형상 인자 및 토질정수의 통계를 보여주며, 이 때, Hw*의 최소값 -1.0은 건조 조건 사면을 의미하며 이에 따라 평균값이 0.5보다 작아진 것을 확인할 수 있다.
Table 1.
Range and distribution of input parameters used in seepage and slope stability analysis
| H (m) | β (-) | γd (kN/m3) | c (kN/m2) | ϕ (°) | Hw* (-) | |
| Min | 10 | 1 | 13.00 | 2 | 30 | -1 |
| Max | 20 | 2 | 22.35 | 22 | 40 | 1 |
| Mean | 15 | 1.5 | 17.64 | 12.03 | 34.96 | 0.286 |
| St. dev. | 3.42 | 0.369 | 2.67 | 5.75 | 2.87 | 0.613 |
매크로 프로그램 ‘AutoHotkey’를 이용하여, 상기의 사면 형상, 토질정수, 지하수위 정규화값이 기록된 엑셀파일로부터 사면해석 프로그램 내에 42,000개의 수치해석 도메인을 생성되도록 자동화하였다.
3. 다층 퍼셉트론 신경망과 모델 훈련
입력층(input layer)과 출력층(output layer) 사이에 여러 개의 은닉층(hidden layer)이 있는 신경망을 심층신경망(deep neural network)이라고 하며, 이러한 심층신경망의 가장 단순한 형태가 다층 퍼셉트론(MLP)이다. 기존의 단층 퍼셉트론은 0 및 1의 서로 다른 두 개 입력인자에 대해서 1을 출력하는 논리회로 XOR 문제와 같이 비선형적으로 분리된 데이터를 훈련할 수 없었으나, 다층 퍼셉트론 신경망에서는 이러한 한계를 극복할 수 있게 되었다(Rumelhart, 1986).
다층 퍼셉트론에서는 훈련 과정에서 인접한 층의 각 노드 사이의 가중치를 임의의 값으로 설정하고 편향의 초기값을 1로 설정한 후, 하나의 훈련 데이터에 대해 각 층의 입력 함수 값을 계산하고 최종적으로 출력 활성화 함수에 의한 값이 계산된다. 식 (2)는 i번째 은닉층의 j번째 노드에서 i-1번째 층으로부터 입력을 받아 활성화 함수(Φ(x))를 통해 출력값(hij)이 계산되는 과정이다. xki-1는 i-1번째 층의 k번째 노드에서의 출력값, n은 i-1번째 층의 노드 개수, bij는 i번째 은닉층 j번째 노드에서의 편향이며, wkji-1는 xki-1와 i번째 은닉층의 j번째 노드 사이의 가중치이다. 마지막 출력층에서의 활성화 함수의 출력값과 실제 값의 차이가 허용오차 이내가 되도록 각 계층의 가중치를 업데이트하고, 모든 훈련 데이터에서 허용오차를 만족하면 훈련을 멈춘다.
다층 퍼셉트론은 은닉층에서 예측한 결과값의 오차를 모델의 역방향으로 전파하면서 가중치를 업데이트하는 역전파 알고리즘을 활용한다. 다층 퍼셉트론은 역전파 알고리즘이 적용된 최초의 심층 신경망이다(Linnainmaa, 1970; Rumelhart, 1986).
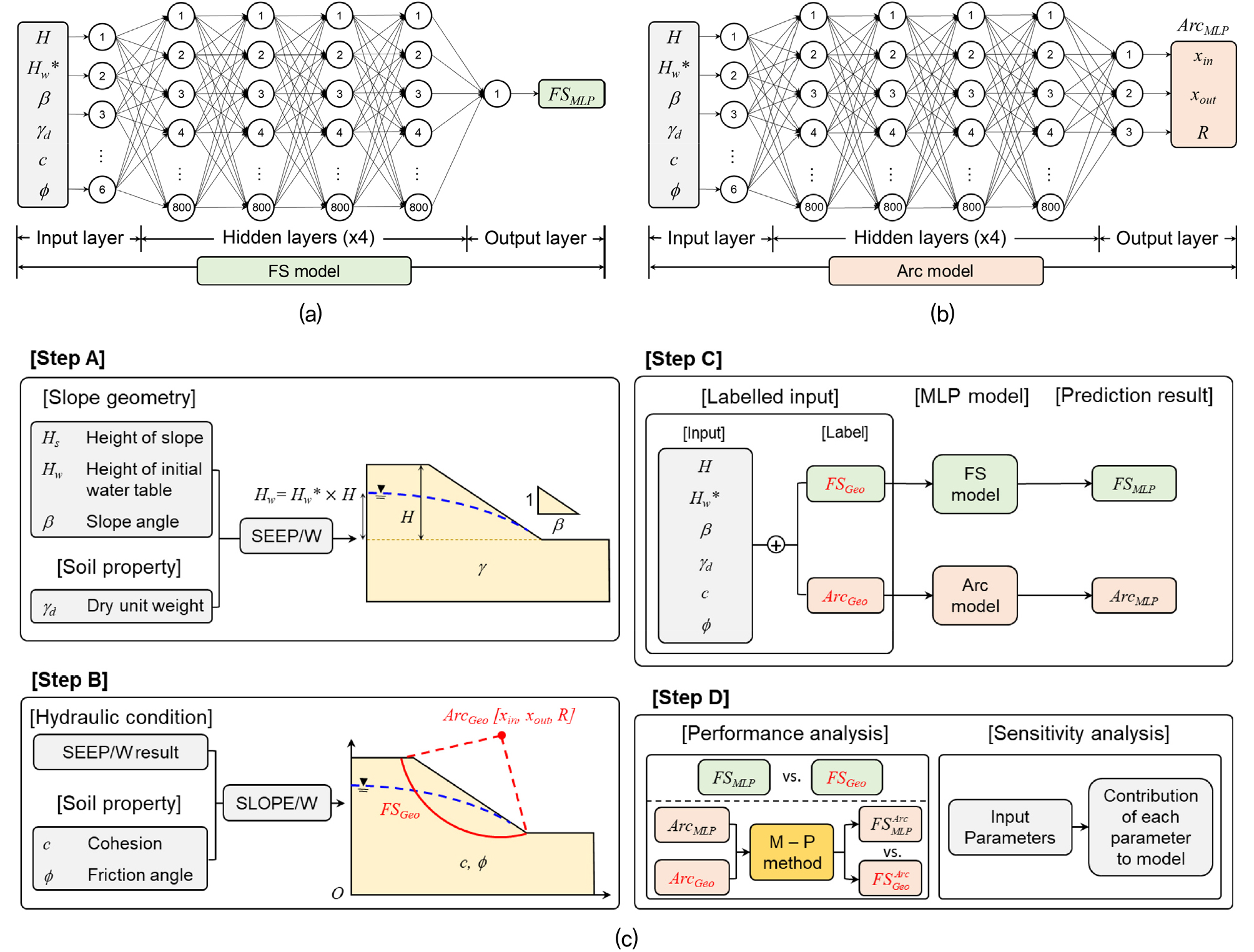
본 연구에서는 6개의 입력값을 이용해 사면의 안전율과 원호 파괴면을 예측하는 회귀분석을 하였다. 일반적으로 회귀분석에는 MLP외에 SVM, XGBoost 등의 다양한 기계학습 알고리즘 들을 적용할 수 있다. MLP모델은 위 두 모델에 비해 구조가 단순하고 모델의 변형이 용이하기 때문에 하이퍼파라미터 튜닝을 통한 모델 최적화가 효율적이다. 따라서 본 연구에서는 사면 안전율 및 파괴 원호 형상의 예측을 위해 두 개의 MLP 회귀모델을 훈련하였다(Fig. 2(a) & 2(b)). 두 MLP 모델의 입력층과 은닉층은 동일하며 6개의 노드로 구성된 입력층 1개와 각각 800개의 노드로 구성된 은닉층 4개로 구성되었다. 출력층의 노드 수는 각각 1개와 3개로, 출력층에 1개의 노드가 있는 MLP 모델(FS model)을 사용하여 안전율 FSMLP를 예측하고, 출력층에 3개의 노드가 있는 MLP 모델(Arc model)을 사용하여 사면의 파괴 원호 인자 ArcMLP (xin, xout, R)를 예측하였다. 입력층과 각 은닉층 사이에 활성화 함수 ReLU를 적용하였고 훈련 과정에서 가중치와 편향을 모두 훈련시키며 진행하였다. 두 모델 모두 500,000의 에포크 동안 0.0001의 학습 속도로 동일한 훈련 조건을 적용하여 훈련을 진행하였다.
Fig. 2(c)는 이 연구의 전체 순서를 설명한다. [Step A]에서 사면 형상 인자인 사면 높이(H), 비탈면 기울기(β), 지하수위 높이(Hw), 토질 정수 건조단위중량(γd)을 매크로 프로그램으로 SEEP/W에 입력하여 침투해석을 수행하였다. [Step B]에서는 [Step A]에서 얻은 SEEP/W 해석 결과와 이전에 설정한 마찰각(ϕ) 및 점착력(c) 조건을 초기 조건으로 사용하였으며, 이를 매크로 프로그램을 이용하여 SLOPE/W 프로그램에 입력한 뒤 사면안정해석을 수행하였다. 사면안정해석을 통해 계산한 사면 안전율(FSGeo) 및 파괴 원호 인자(ArcGeo : xin, xout, R)를 획득하였다. [Step C]에서는 사면의 안전율을 예측하는 Fig. 2(a)의 MLP 모델(FS model)과 사면의 파괴 원호를 예측하는 Fig. 2(b)의 MLP모델(Arc model)을 각각 훈련하였다. 훈련은 입력된 H, β, γd, c, ϕ, Hw* 에 대해 모델이 예측한 안전율 FSMLP와 파괴원호 ArcMLP (xin, xout, R)가 각각 [Step B]에서 준비한 레이블 FSgeo 및 ArcGeo에 근사하도록 수행하였다.
마지막으로 [Step D]에서 SLOPE/W를 이용한 사면안정해석 결과와 훈련한 MLP모델의 예측 결과를 비교하여 모델의 성능을 정량적으로 평가하였다. FS model의 경우, SLOPE/W 해석 결과 FSGeo와 모델 훈련 결과 FSMLP를 직접 비교하는 방식으로 모델의 성능을 평가하였다. Arc model의 경우 SLOPE/W 해석으로부터 얻은 파괴원호 ArcGeo (xin, xout, R)와 모델이 예측한 파괴원호 ArcMLP (xin, xout, R)로부터 Morgenstern-Price 방법(M-P method)으로 각각 계산한 안전율 FSGeoArc와 FSMLPArc을 비교하여 모델의 성능을 평가하였다. 한편, 민감도 분석을 수행하여 입력 인자가 예측 모델의 출력 인자에 미치는 기여도에 대해 고찰하였다. Fig. 2(c)의 [Step C]와 [Step D]에서 안전율 예측과 관련된 과정은 연두색 상자로, 사면 파괴원호 예측과 관련된 과정은 분홍색으로 표시하였고, SLOPE/W 해석 결과로 참값으로서 MLP모델이 예측한 결과의 비교 대상이 되는 실제 값은 붉은색으로 표기하였다.
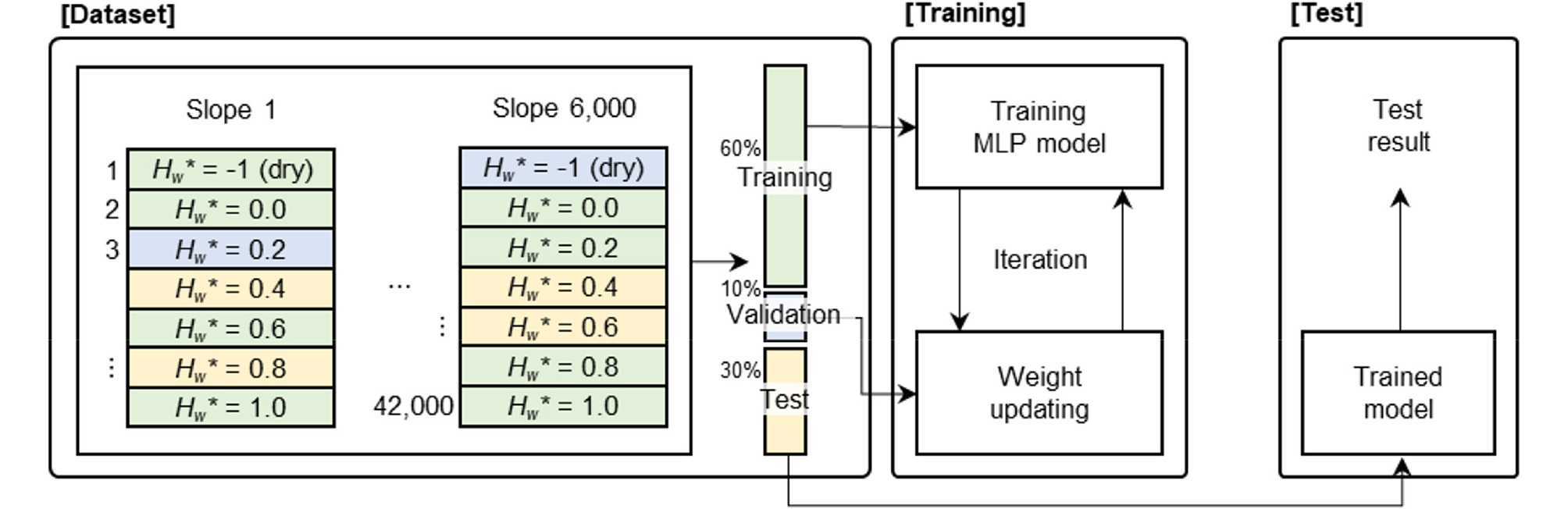
Fig. 3은 MLP모델의 훈련데이터 구성을 나타낸다. 6,000개의 사면 도메인과 각 도메인당 7개의 지하수위 조건으로 구성된 총 42,000개의 데이터를 훈련(training), 검증(validation), 시험(test)을 위해 6:1:3의 비율로 무작위로 분리하였다. 본 연구에서 사용된 두 모델의 훈련에 동일한 비율로 분리된 데이터셋이 적용되었다. 검증 데이터는 훈련 과정에서 모델이 훈련용 데이터에 과적합(overfitting)하는 것을 확인하기 위한 것으로 모델의 훈련에는 관여하지 않으며, 시험 데이터는 훈련이 끝난 모델의 성능을 평가하기 위한 것이다. 500,000번의 에포크 동안 훈련 과정을 반복한 후 훈련이 완료된 모델에 시험 데이터를 입력하여 모델의 시험 결과 FSMLP및 ArcMLP를 얻는다.
4. 결 과
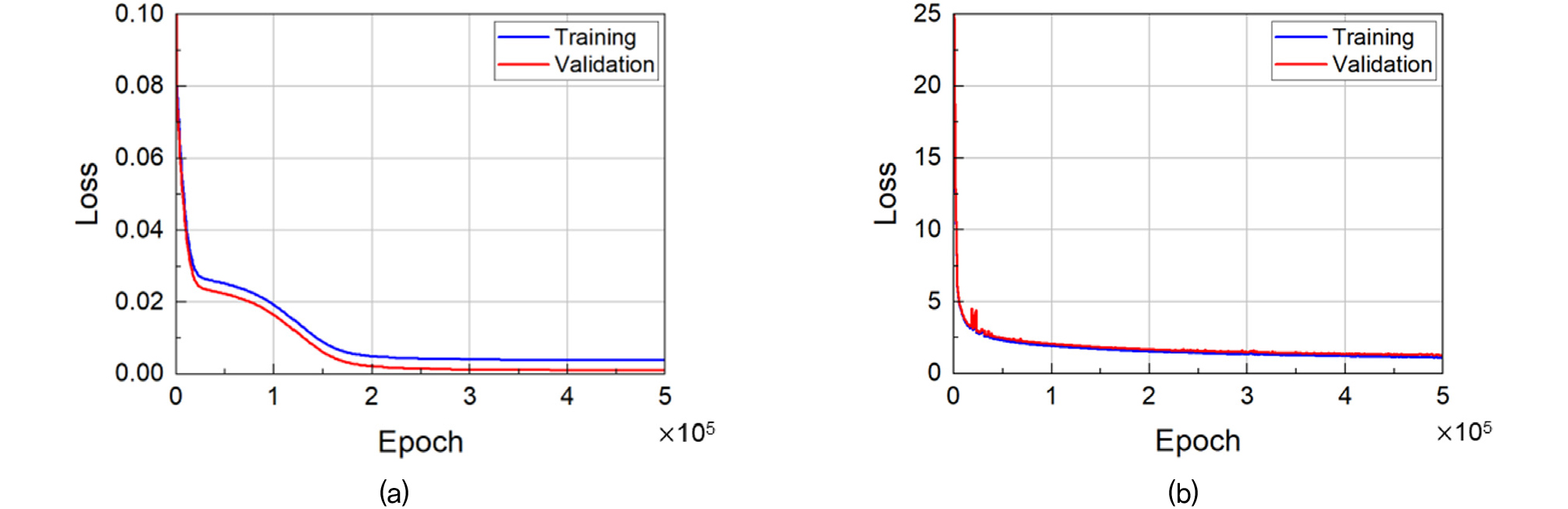
훈련한 FS model과 Arc model의 에포크 증가에 따른 손실함수의 수렴을 Fig. 4에 나타내었다. Fig. 4(a)는 사면의 안전율을 예측하는 FS model, Fig. 4(b)는 사면의 원호파괴면을 예측하는 Arc model의 손실함수가 에포크 500,000에 도달하며 수렴한 모습을 보여준다. 두 모델 모두 훈련 과정에서 손실함수 값이 크게 진동하지 않고 수렴하였으며, Fig. 4(a)에서 그래프가 변곡점을 가지지만 최종적으로 수렴했다는 점에서 모델을 훈련시키기 위한 훈련 스케줄이 적절했다고 판단된다.
4.1 사면의 안전율 예측
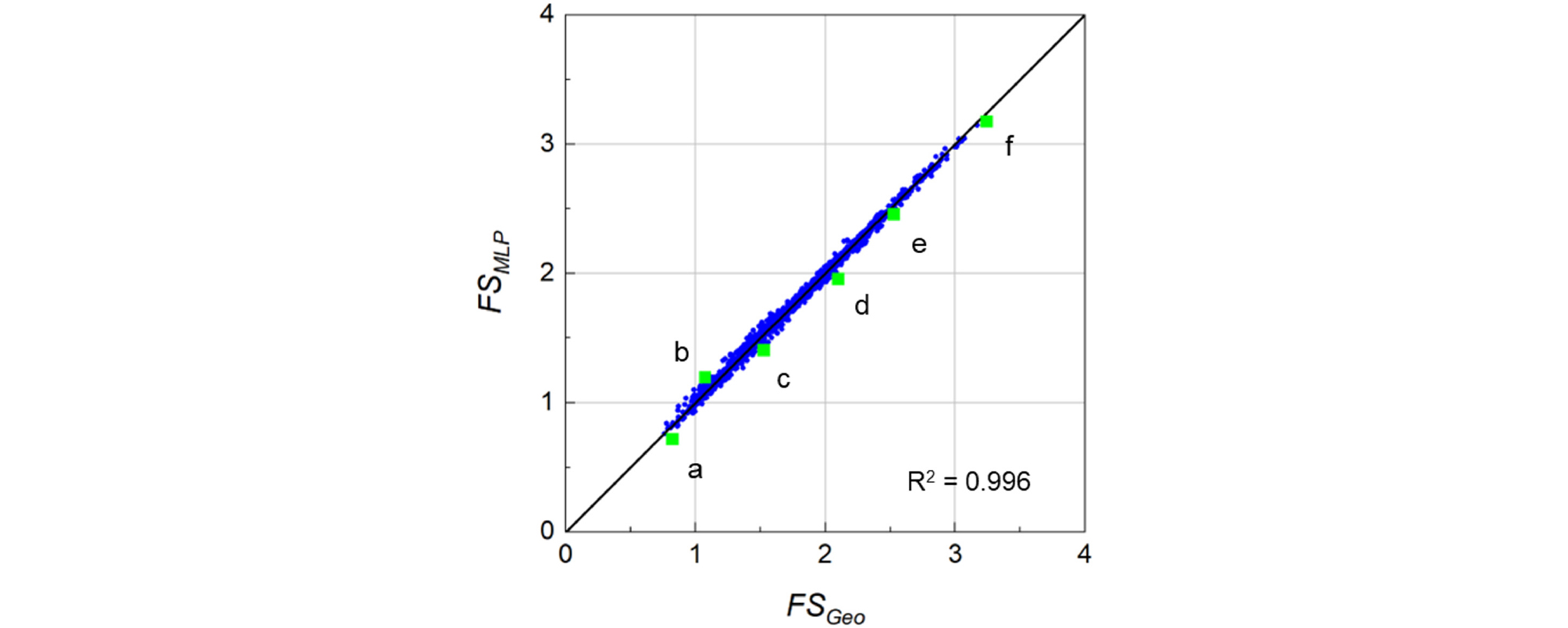
Fig. 5는 SLOPE/W 프로그램을 이용하여 구한 사면의 실제 안전율(FSGeo)과 본 연구에서 훈련된 FS model이 예측한 안전율(FSMLP)을 비교한 결과를 보여준다. 12,600개의 시험 데이터의 실제 안전율과 예측 안전율 사이의 결정 계수와 평균 제곱 오차는 0.996과 0.0005로 각각 1과 0에 매우 가까운 수치로 이전 연구에서 보고된 모델의 성능과 유사하다(Erzin and Cetin, 2013; Rukhaiyar et al., 2018). 예측 오차(|FSMLP - FSGeo|)가 실제 안전율(FSGeo)의 5% 보다 큰 경우는 총 133개로 전체 시험 데이터 개수의 1.05%에 해당하고, 1.0 보다 작은 실제 안전율을 1.0 보다 크게 혹은 1.0 보다 큰 실제 안전율을 1.0 보다 작게 예측하는 경우는 38개로 전체 테스트 데이터 개수의 0.30% 이내였다.
Fig. 6(a) ~ 6(f)는 Fig. 5에서 a~f로 표시한 데이터들의 SLOPE/W 해석 결과를 사면의 단면으로 나타낸 것이다. a, d 및 e에 해당하는 지하수위가 존재하는 해석 도메인에 대한 결과에서는 사면 내 간극수압을 크기에 따라 도시하였으며, 건조 사면 (b, c 및 f)은 하늘색으로 표시하였다. 지하수위는 파란 점선으로, 사면의 파괴원호는 검은 실선으로 표시하였다. a~f는 각각 안전율을 0.5~1.0, 1.0~1.5, 1.5~2.0, 2.0~2.5, 2.5~3.0, 3.0~3.5의 여섯 구간으로 나누어 그 구간에서 프로그램의 해석 결과와 FS model의 예측 결과가 가장 큰 오차를 가지는 경우에 해당한다.
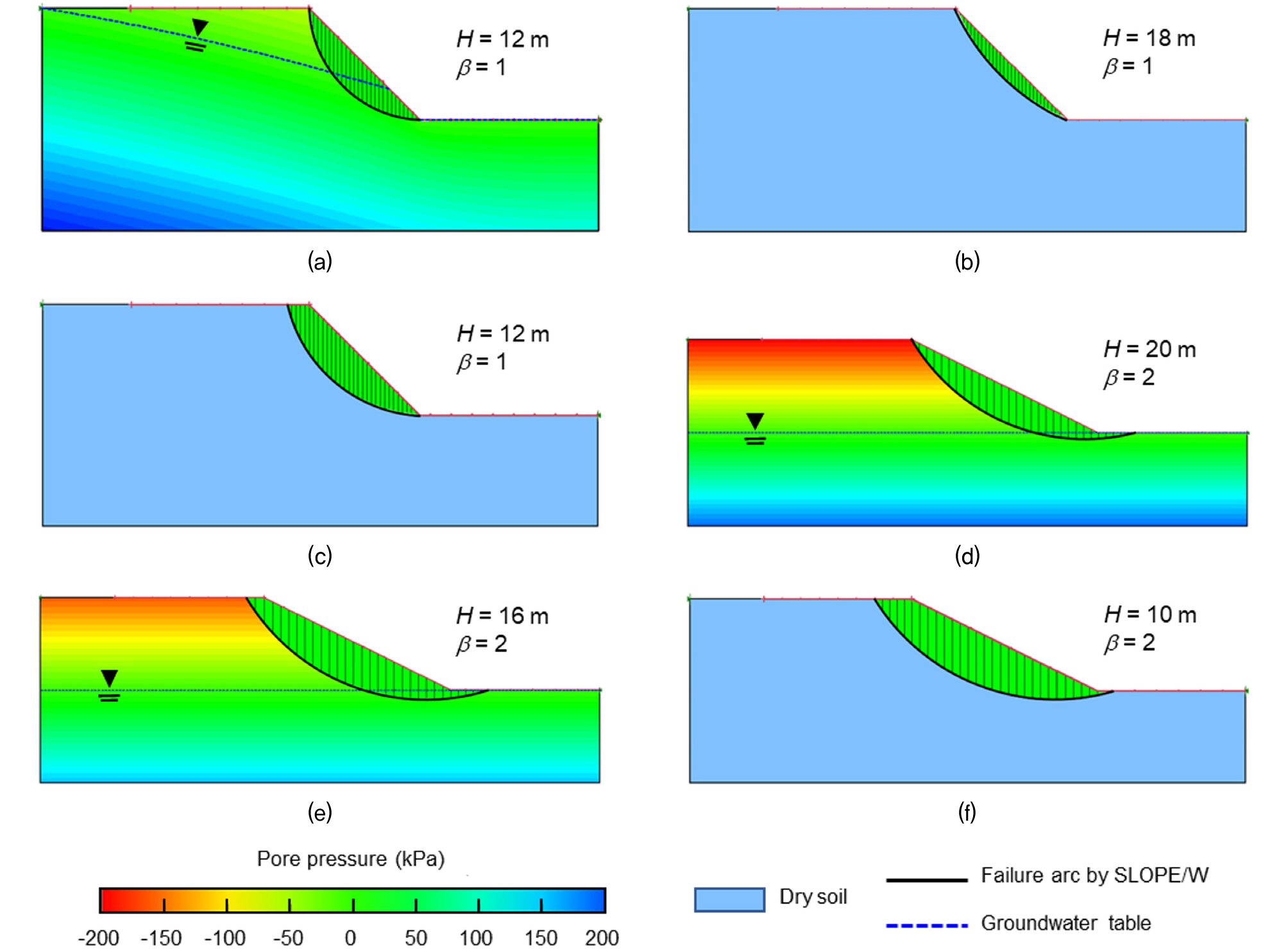
Fig. 6
SLOPE/W results at (a) point a, (b) point b, (c) point c, (d) point d, (e) point e, and (f) point f in Fig. 5
해석 결과, 비탈면 기울기가 완만할수록 (β=2) 저부파괴가 발생하였다. 건조 사면의 경우, 사면의 높이가 클수록 안전율이 낮아졌으나, 지하수위가 존재하는 경우에는 모관흡수력의 영향으로 안전율의 경향이 건조사면의 경우와 일치하지 않았다. 한편, 지하수위로 인해 모관흡수력의 영향을 받은 해석 도메인 a, d 및 e의 경우, 실제 안전율에 비해 모두 예측 안전율이 과소평가되었다(Table 2). 반면, 건조 사면의 경우 (b, c 및 f), 실제 안전율이 1에 가까운 b 경우에 대해서는 FS model이 안전율을 과대평가하였으나 c 및 f 경우에 대해서는 모두 과소평가하였다. 그러나, 오차가 큰 경우 FS model이 대부분 안전율을 과소평가한다는 것은 구조물 안정성 측면에서 긍정적으로 작용할 것으로 판단된다. 결과적으로, FS model은 학습을 통해 200개 토질정수 조건에 대한 선단파괴 및 저부파괴 패턴을 보인 해석결과를 합리적으로 예측한 것으로 판단된다.
Table 2.
Input parameters, factor of safety, and error of data corresponding to a~f in Fig. 6
4.2 사면의 파괴 원호 예측과 Morgenstern-price 방법을 통한 정량적 평가
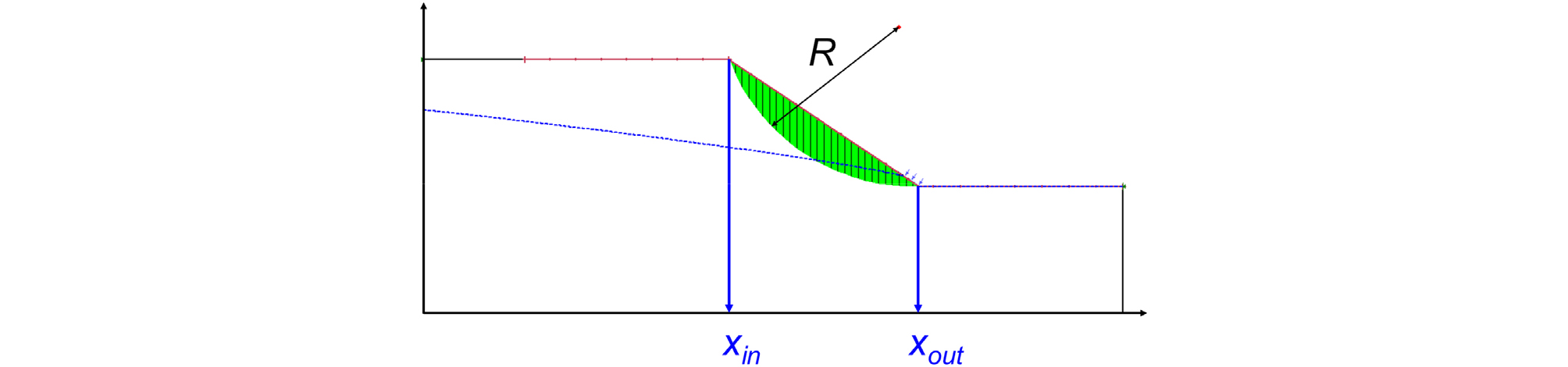
본 연구에서는 임계활동면의 양쪽 끝 횡좌표(xin, xout)와 반지름(R)으로 원호파괴면을 표현하였다. SEEP/W 및 SLOPE/W를 거쳐 계산된 해석결과의 원호파괴면로부터 위 3개 인자를 도출하였고, 이를 Fig. 2b의 Arc model의 학습 중 레이블로 이용되었다(Fig. 7).
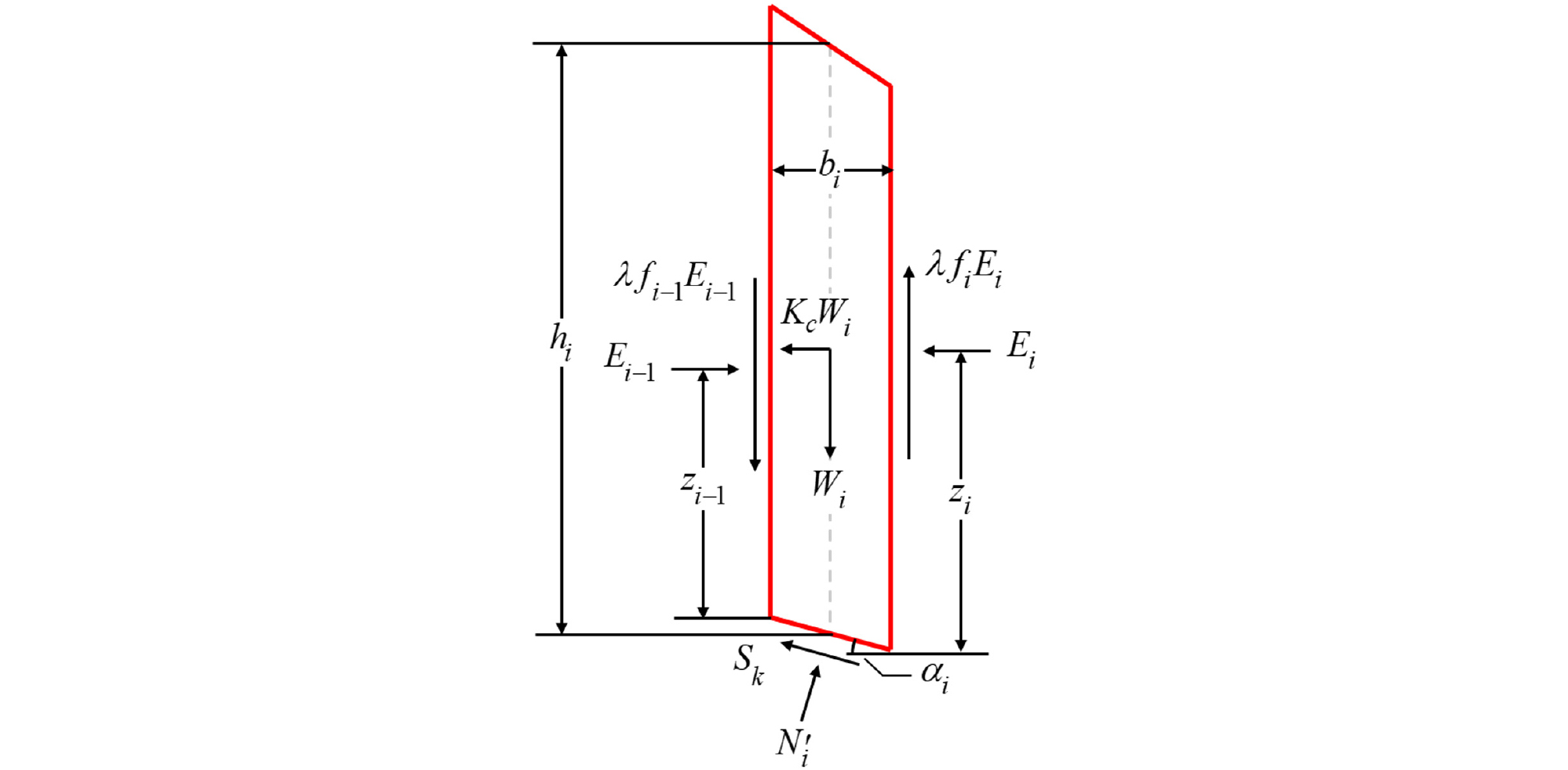
Arc model의 성능을 정량적으로 평가하기 위해 모델이 예측한 파괴 원호의 안전율을 절편법을 이용하여 구하고 그 값을 비교하였다. 프로그램을 이용하여 한계평형해석을 할 때 불포화토에서의 모관흡수력으로 인한 유효응력 증가를 고려하였기 때문에 지하수위가 있는 케이스는 단순하게 절편법을 이용하여 안전율을 구하기에 어려움이 있다. 따라서 시험 데이터 중 건조 사면의 해석 결과에 대해 Morgenstern-Price 방법을 사용하여 Arc model이 예측한 원호파괴면의 안전율을 계산하고 같은 방법으로 SLOPE/W에서 계산한 안전율과 비교하였다. Fig. 8에 상재 하중이 없는 건조 사면의 원호 파괴 토체에서 i번째 절편에 작용하는 하중을 간략히 도시하였다(Zhu, 2005). 파괴 토체의 i번째 절편에서 Wi는 자중, hi, bi는 각각 높이와 폭, αi는 저부의 경사, Kc는 수평지진계수, Ei, Ei-1은 각각 절편의 오른쪽과 왼쪽에 작용하는 수직 하중, zi, zi-1는 Ei, Ei-1가 작용하는 지점의 높이, Ni'는 절편의 아래에 작용하는 수직항력, Sk는 k번째 반복에서의 전단강도이다. λfi, λfi-1는 수평하중과 수직하중의 비율이며 함수 λf(x)로 표현되고 f(x)는 식 (3)으로 정의된다. λ는 안전율과 같이 반복을 통해 수렴에 도달하는 값이다. 각 절편에서의 힘, 모멘트 평형을 모두 고려하여 식 (4)를 통해 전체 파괴 토체에 대해서 안전율이 수렴에 도달하는 k번째 반복에서의 i번째 절편의 안전율을 구할 수 있다.
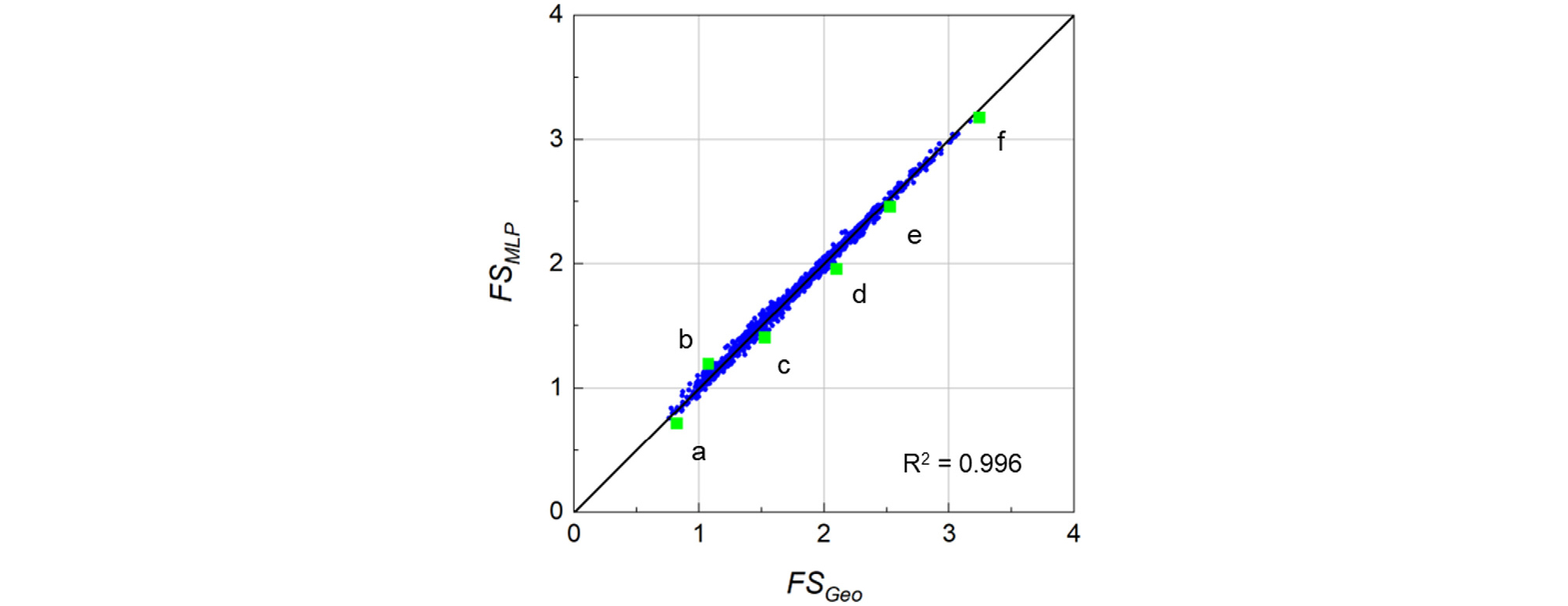
Fig. 9는 훈련한 Arc model이 예측한 파괴원호의 안전율(FSMLPArc)을 SLOPE/W에서 산출한 파괴원호의 안전율(FSGeoArc)과 비교한 결과이다. 시험 데이터 중 지하수위가 있는 사면의 경우는 제외하고 건조한 사면에 대한 데이터 1,829개에 대하여 비교를 진행하였으며, 두 안전율 모두 파괴 원호로부터 계산한 결과이다. 결정 계수는 0.999이고 평균 제곱 오차는 0.0001로 계산되었다. 예측 오차의 크기가 실제 값의 5%이상인 데이터는 없으며, 안전율이 1.0 보다 작은 것을 1.0 보다 크게 혹은 1.0 보다 큰 것을 1.0 보다 작게 예측하는 경우는 4개로 전체 시험 데이터 개수의 0.20%에 불과하여 안전율을 직접 예측하도록 훈련시킨 FS model 보다 더 좋은 예측 성능을 보여주었다. 이것은 원호파괴면을 예측하는 것이 모델 입장에서 안전율을 직접 예측하는 것보다 더 명확할 수 있음을 의미한다.
Fig. 10(a) ~ 10(f)는 Fig. 9에서 a~f로 표시한 데이터들의 SLOPE/W 해석 결과와 Arc model이 예측한 사면의 파괴원호를 나타낸 것이다. SLOPE/W의 결과로 도출된 사면의 파괴원호는 검은 실선으로, Arc model 이 예측한 사면의 파괴원호는 붉은 실선으로 표시하였다. a~f는 각각 안전율을 0.5~1.0, 1.0~1.5, 1.5~2.0, 2.0~2.5, 2.5~3.0, 3.0~3.5의 여섯 구간으로 나누어 그 구간에서 FSGeoArc와 FSMLPArc가 가장 큰 오차를 가지는 케이스를 선택하여 보여주고 있다. 비탈면 기울기와 토질정수는 넓은 분포를 가졌으나, 12m 이하의 상대적으로 규모가 작은 사면이었으며 대부분 선단파괴가 발생했다(Table 3). 이는 MLP모델이 회귀학습을 하며 역전파 알고리즘을 통해 오차를 줄여나가는데, Hw*을 제외한 입력 인자가 정규화되지 않은 실제 값이기 때문에 같은 수준의 오차율이 발생하여도 규모가 작은 사면 도메인에 더 큰 영향을 미치는 것으로 판단된다.
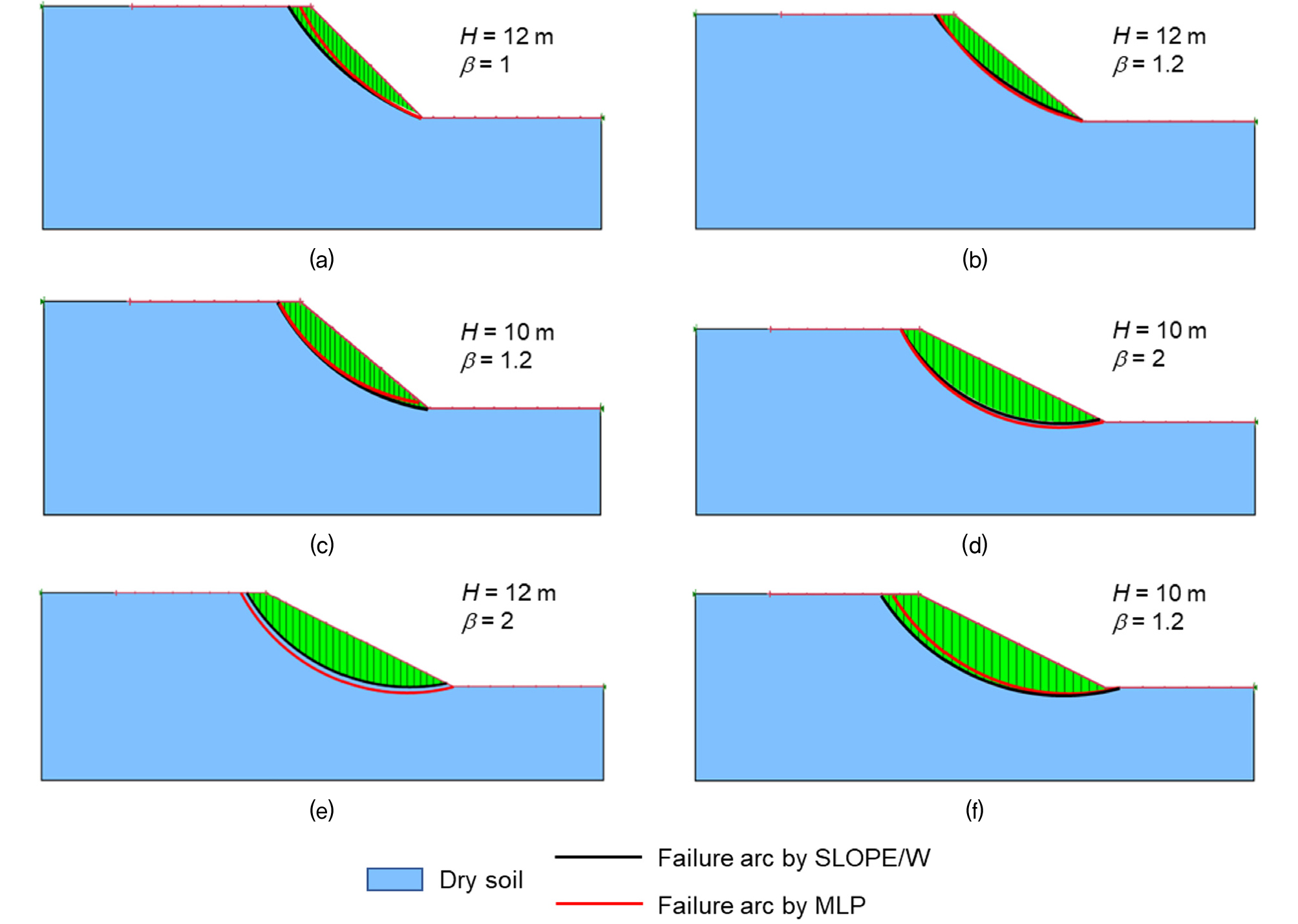
Fig. 10
SLOPE/W and MLP model results at (a) point a, (b) point b, (c) point c, (d) point d, (e) point e, and (f) point f in Fig. 9
Table 3.
Input parameters, factor of safety, and error of data corresponding to a~f in Fig. 10
Fig. 9의 c 데이터를 보면 SLOPE/W에서 구한 파괴 원호로부터의 안전율(FSGeoArc)이 Arc model로부터 구한 파괴 원호로부터의 안전율(FSMLPArc)보다 과소평가되었다. 이것은 SLOPE/W가 사면안정해석을 하는 과정에서 발생한 오차인데, 모든 해석 과정에서 xin, xout, R이 가질 수 있는 값을 그 구간 내에서 8, 16, 8개로 하였다. 그에 따라 생성되는 총 210개의 사면 파괴 원호 중 가장 낮은 안전율을 가지는 데이터를 임계활동면으로 결정한다. c 데이터에서 xin, xout, R이 가질 수 있는 값을 24, 48, 24개로 늘려 총 27×210개의 사면 파괴 원호 중 가장 낮은 안전율을 가지는 데이터를 고르도록 더 정밀하게 분석하면 그때의 FSGeoArc는 1.909에서 1.853으로 FSMLPArc와의 오차가 0.001로 감소한다. 더 정밀하게 분석한 c의 SLOPE/W 해석 결과와 Arc model 예측 파괴 원호가 더 유사해진 것을 확인할 수 있다(Fig. 11).
4.3 모델 입력 인자의 민감도 분석
회귀분석 모델에서 민감도 분석을 수행하여 입력 인자의 출력 인자에 대한 기여도를 평가할 수 있다(Yeung, 2010; Lin et al., 2022). 이는 입력 인자가 입력된 후 모델 안에서 계산되어 출력 인자가 되기까지의 가중치를 비교하여 회귀분석 모델에서 각 입력 인자가 출력 인자에 얼마나 영향을 미치는지 비교하는 방법이다. 값이 높을수록 큰 기여도를 가지는 인자라고 할 수 있다. 본 연구에서 제안하는 MLP모델에서 입력 인자의 기여도에 대해 알아보기 위해 글로벌 민감도 분석을 수행하였다. 민감도 분석은 모든 입력 요소의 변화가 동시에 이루어지고 민감도 분석이 각 입력 인자의 전체 범위에 대해서 수행될 때 글로벌 민감도 분석으로 간주한다(Iooss and Lemaître, 2015).
글로벌 민감도 분석의 방법으로는 OAT(One Factor at a Time) 방법, Sobol 방법, Morris 방법 등이 대표적으로 이용된다(Daniel, 1973; Sobol, 1990; Morris, 1991). 본 연구에서는 계산 비용이 적게 드는 Morris 방법을 이용하여 MLP모델에서 6가지 입력 인자 H, β, γd, c, ϕ, Hw* 가 출력 인자인 FS, xin, xout, R에 미치는 영향을 분석하였다. Morris 방법은 편미분을 수행하여 식 (5)와 같이 i번째 입력 인자(xi) 변화량에 대한 출력 인자 변화율을 i번째 입력 인자의 기여도 EEi(elementary effect)로 평가한다. 이 때, xi와 (xi + Δ)의 범위가 입력 인자의 전체 영역에 해당하기 때문에 글로벌 분석에 해당한다. 식 (5)~(7)을 통해 각 입력 인자 EEi의 평균(μi)과 분산(σi)을 구할 수 있다. j는 총 관측횟수 r 중 차례를 나타내며, 본 연구에서는 총 관측횟수 r을 40으로 설정하였다.
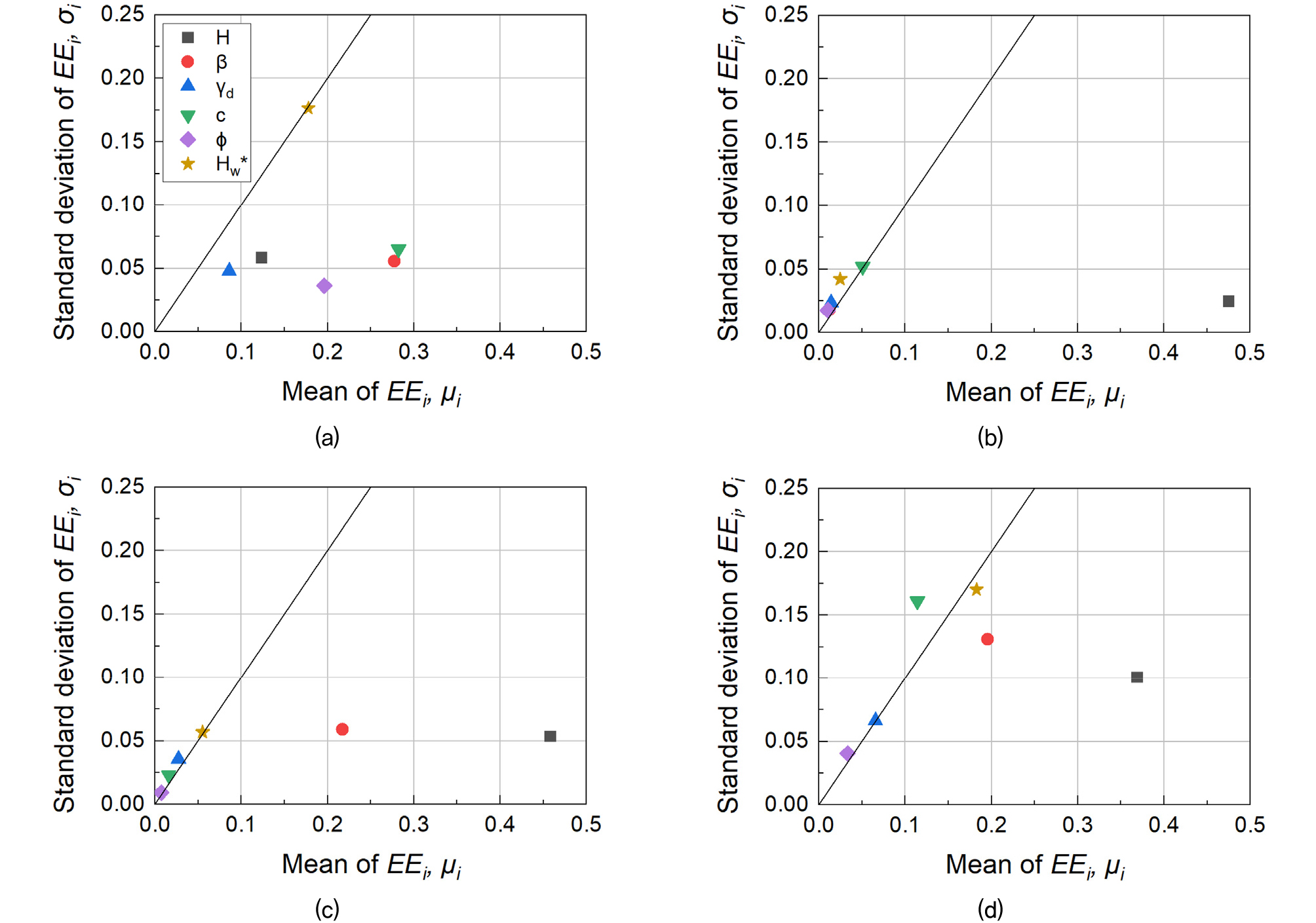
사면의 안전율을 예측하는 FS model에서 입력 인자들의 민감도는 점착력, 비탈면 기울기, 마찰각, 사면높이로 정규화된 지하수위 높이, 사면높이, 단위중량 순으로 나타난다(Fig. 10(a)). 이 순서는 기존에 보고된 문헌과 유사하며 전통적인 방법의 사면안정해석에서 사면의 파괴에 지배적인 영향을 미치는 인자들이 점착력, 마찰각, 비탈면 기울기 등이라는 점과도 일관된다(Shang et al., 2021; Hamm et al., 2006).
사면의 파괴 원호에 대한 민감도 분석 결과는 사면의 파괴 원호를 표현하는 세 가지 인자인 xin, xout, R을 예측하는 MLP모델에서 입력 인자들의 민감도를 세 가지 출력 인자에 대해 각각 수행하였다(Fig. 10(b) ~ 10(d)). 각 출력 인자별로 입력 인자들의 민감도 순위에 차이가 있지만 공통적으로 사면의 형상을 나타내는 사면높이가 가장 높은 순위에 있다. 이것은 출력인자가 정규화된 값이 아닌 단위를 가지는 값이기 때문에 사면의 규모를 나타내며 같은 단위를 가지는 사면높이에 가장 큰 영향을 받는 것으로 판단된다. 또한 출력값 중 xout이 가질 수 있는 값의 범위는 비탈면 기울기에도 영향을 받기 때문에 비탈면 기울기도 xout을 예측하는데 큰 영향을 미친 것으로 보인다(Fig. 10(c)).
Fig. 10의 mean sensitivity - standard deviation 그래프에서 데이터가 y=x보다 위에 존재하면 그 입력인자는 출력인자와 비선형적인 관계를 가지는 것으로 해석할 수 있다(Tian, 2013; Kong et al., 2015). 본 연구에서 훈련한 Arc model에 대해 사면 높이를 제외한 모든 인자가 출력인자 xin과 비선형적인 관계에 있고, 사면높이와 비탈면 기울기를 제외한 모든 인자가 출력인자 xout과 비선형적인 관계에 있으며, 점착력과 마찰각이 R과 비선형적인 관계를 가지는 것으로 나타났다. SEEP/W를 이용한 지하수의 침투해석 결과를 SLOPE/W에 적용하여 사면안정해석을 수행할 때 불포화토의 모관흡수력을 적용하였기 때문에 사면높이로 정규화된 지하수위의 높이(Hw*)가 출력인자들과 비선형적인 관계를 보이는 부분이 일부 존재하는 것으로 확인되지만 전체 데이터에서 비선형적인 관계를 가지지는 않는 것을 민감도 분석을 통해 확인하였다.
5. 요약 및 결론
본 연구에서는 간단한 형태의 심층신경망인 다층 퍼셉트론을 이용하여 사면안정해석을 수행하였다. 다층 퍼셉트론 신경망 모델의 훈련에는 다양한 사면과 지하수의 분포, 토질정수로부터 SEEP/W 및SLOPE/W를 이용하여 총 42,000개의 데이터를 생성하였다. 데이터 생성에 사용된 사면은 하나의 층으로 구성된 단순 사면이며, 사면의 지반조건은 세립분이 포함된 사질토로 가정하여 해당하는 물성을 부여하였다.
(1) SLOPE/W를 통해 생성한 훈련 데이터를 이용하여 다층 퍼셉트론 신경망(FS model)을 통해 사면의 안전율을 예측하도록 훈련시켰다. SLOPE/W의 결과(FSGeo)와 모델의 훈련 결과(FSMLP)를 비교한 결과 결정계수 0.996로 매우 우수한 성능으로 안전율을 예측할 수 있음을 보였다.
(2) SLOPE/W를 통해 생성한 훈련 데이터를 이용하여 다층 퍼셉트론 신경망(Arc model)을 통해 사면의 파괴 원호를 예측하도록 훈련시켰다. 파괴 원호를 예측하는 성능을 정량적으로 평가하기 위해 Arc model이 예측한 임계활동면의 안전율(FSMLPArc)과 SLOPE/W에서 도출한 원호파괴면의 안전율(FSGeoArc)을 Morgenstern-Price 방법으로 계산하여 비교하는 방법을 제시하였다. 이 검증 방법을 통해 원호파괴면을 예측한 Arc model의 성능이 우수함을 보였고, 결정계수는 0.999로 나타났다. 이는 단순히 안전율을 타겟으로 하여 훈련시킨 결과보다 우수하며 훈련 결과로서 안전율뿐 아니라 원호파괴면에 대한 정보까지 얻을 수 있다는 점에서 두 방법 중 더 활용 범위가 넓다.
(3) Morris 민감도 분석을 통해 사면안정해석에서의 입력 인자의 출력 인자에 대한 기여도를 분석하였다. 사면의 안전율을 직접 예측하는 경우에는 토질의 물성에 해당하는 c, ϕ가 상대적으로 높은 기여도를 가지고 사면의 파괴 원호를 예측하는 경우에는 사면의 형상에 해당하는 H, β가 상대적으로 높은 기여도를 가지는 것으로 나타났다. 또한 여러 입력 인자가 출력 인자와 비선형적 관계를 가진다는 결과로부터 사면안정해석을 위한 인공지능 모델로 비선형적 데이터에 대해 훈련이 가능한 다층 퍼셉트론을 사용한 것이 적합하였다고 할 수 있다.
(4) 안전율 및 파괴패턴에 대한 결과를 분석한 결과, 대부분 선단파괴가 발생하였고, 저부파괴가 소수 존재하였으며 사면 내 파괴는 거의 발생하지 않았다. 파괴 패턴에 관한 훈련모델의 일반적인 적용을 위해서는 향후 여러 층의 토질로 이루어진 사면 또는 더 다양한 토질 조건에서의 해석 결과를 바탕으로 한 훈련이 필요할 것으로 판단한다.