1. 서 론
2. 실내모형시험
2.1 재료 및 시료 조성
2.2 실험장치 및 방법
2.3 실내모형실험 결과
3. DEM을 활용한 수치해석
3.1 시료 조성 방법
3.2 시료의 전단거동 검증 및 시료 조성 조건
3.3 말뚝 관입의 모델링
4. 모델링 분석 결과 및 수치해석결과 비교
4.1 흙 입자 간의 상호작용 검증
4.2 초기 관입 속도의 영향
4.3 수치해석과 실내모형시험의 결과 비교
5. 결 론
1. 서 론
개단말뚝은 깊은 기초의 한 종류로서 말뚝 관입 시 말뚝의 내부 공간으로 흙의 유입을 허용한다. 이에 따라 관입이 진행될 때 다른 형태의 말뚝과 비교하여 관입저항력이 과도하게 유발되지 않아 시공성이 우수하며 말뚝의 손상이 적은 장점을 가지고 있다. 그리고 말뚝의 내부로 유입된 흙의 저항이 증가되는 충분한 관입 깊이에 도달하면 일반적인 폐단말뚝에 준하는 지지력이 발현된다고 알려져 있다(Lehane and Randolph, 2002). 이러한 개단말뚝의 장점으로 인해 풍력발전, 항만 등의 해안 기초구조물뿐만 아니라 장대교량, 초고층 빌딩 등 많은 구조물의 기초로 널리 사용되고 있다.
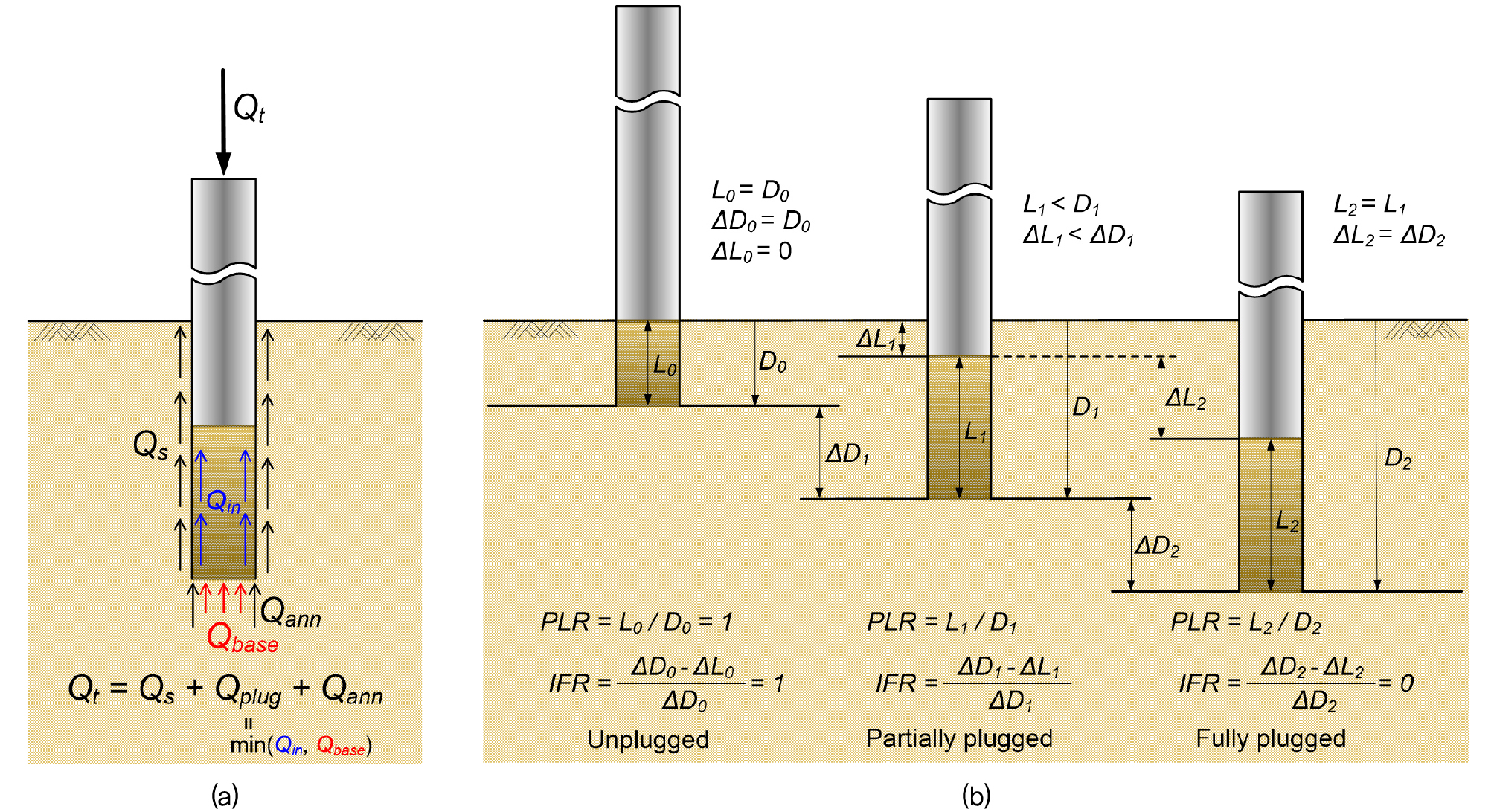
앞서 설명한 것과 같이 개단말뚝의 관입 시 그 내부로 유입되는 흙을 ‘관내토’라고 하며, 관입이 진행됨에 따라 Fig. 1(a)와 같이 관내토에는 내주면과의 마찰력(Qin)과 관입면 하부로부터의 추력(Qbase)이 발생한다. 이 두 힘 간의 상호작용으로 인해 관내토의 응력 상태가 변화하며 이는 개단말뚝의 동적 거동 특성과 말뚝의 극한지지력에 큰 영향을 미쳐 이에 관한 연구가 주로 진행되었다(Paikowsky et al., 1989; Brucy et al., 1991).
기존 문헌에서는 말뚝의 관입 깊이에 대한 관내토의 길이의 비율을 척도로 하여 Fig. 1(b)와 같이 관내토의 상태를 세 가지 상태로 분류 해석하였다(Paik and Lee, 1993; Jardine et al., 2005; Ko and Jeong, 2015). 관내토 상태를 알려주는 가장 일반적인 지표는 Plug Length Ratio(PLR)와 Incremental Filling Ratio(IFR)로 전자는 특정 항타 단계에서 관내토의 길이(L)를 전체 관입 깊이(D)로 나누어 구하며, 후자는 특정 항타 단계에 대하여 직전 상태로부터 해당 항타에 의해 증가한 관내토의 길이(ΔL)를 관입 깊이 증가량(ΔD)으로 나누어 구한다. 이 두 지표는 아래 식과 같이 표현할 수 있다.
위 연구들은 최종 관입 상태에서의 길이 지표(e.g. PLR and IFR)와 내주면 마찰력, 주면 마찰력 등 개단말뚝의 지지력을 구성하는 성분을 분석하여 관내토의 거동을 분석하였고, 이런 관내토의 상태에 미치는 영향 요소들에 관해서도 연구가 이루어졌다. 관내토 상태에 영향을 미치는 대표적인 세 가지 인자는 지반 조건(Paik and Salgado, 2003; Ko et al., 2022), 말뚝 형상(Paikowsky, 1989; Li et al., 2021), 관입 방법(Brucy, 1991; Lu et al., 2023)이 있다.
하지만, 관입 단계에서의 항타성과 지지력 발현에 영향을 미치는 관내토 내부 응력 상태의 발달 과정을 분석한 연구는 극히 드물다. 이론적인 접근의 경우 동적 관입 과정에서 수반되는 관내토 거동의 불확실성을 반영하기 어렵고, 실험적 연구의 경우 역시 관입 과정에 따라 변화하는 관내토 내부의 응력을 측정하기엔 한계를 가지고 있다(Henke and Bienen, 2013). 따라서, 이를 극복하기 위해 수치해석적 방법이 도입되기 시작하였으며, 말뚝의 관입 과정과 같은 대변형 해석에 있어서 지반을 개별 입자들의 군락으로 해석하는 이산요소법(Discrete Element Method, DEM)을 통한 분석 연구들이 주목받아 왔다. 1990년대부터 Cone Penetration Test(CPT)에 관한 연구(Huang and Ma, 1994)를 시작으로 흙 입자와 말뚝의 상호관계 연구를 위한 DEM 모사에 있어서 필수 요소인 접촉 모델의 기본적인 입력 인자(마찰계수, 강성 등)의 영향 평가 연구가 이루어졌다(Kinloch and O’Sullivan, 2007). 특히, 2010년대 중반에 들어서 개단말뚝의 관입에 의한 지중 응력의 정량적 해석을 위한 체계적인 모델링이 시도되기 시작했다(Li and Li, 2014; Li et al., 2019). 하지만, 기존의 흙 입자와 말뚝의 상호관계 연구에서는 가장 기본적인 접촉 모델인 선형 모델(Linear Model)을 이용해 지반을 2차원에 모사하였는데, 해당 접촉 모델의 한계로 인해 현실적인 내부마찰각을 모사하지 못하거나 입자의 회전이 과대평가 되는 문제를 가지고 있었다. 이에 Li et al.(2021)은 접촉 모델에 회전 저항성을 반영하는 Rolling Resistance Linear Model(RRLM)을 사용함으로써 위 문제를 해결하여 흙 입자 간 접촉에 있어서 실제와 같은 거동의 검증은 입증되었으나, 흙 입자-말뚝 간의 거동에 대한 검증까지 시행되지 않아 관내토 거동 평가 결과의 신뢰성이 떨어지는 문제를 가지고 있다.
이에 본 연구에서는 상용 이산요소해석 프로그램인 Particle Flow Code(PFC)를 활용하여 개단뚝의 관입 과정을 단계별로 모사하였으며, 이 과정에서 말뚝 내부에 형성되는 관내토의 길이 변화를 실내모형말뚝 실험 결과를 활용하여 흙 입자-개단말뚝 간의 거동을 검증하였다. 이뿐만 아니라 흙 입자의 회전 저항성을 고려하는 RRLM을 적용하여 흙 입자 간의 거동 역시 실제 측정치와의 검증을 통해 개단말뚝의 관입 과정 중 변화하는 관내토의 거동 분석에 있어 더욱 신뢰성 있는 결과를 도출하였다. 또한, 본 연구에서 도출된 결과를 통하여 향후 DEM을 활용한 개단말뚝의 관내토 거동 연구 과정에서 발생할 수 있는 시행착오를 최소화하고자 말뚝의 관입단계별 모델링을 소개하고, 관내토 거동에 영향을 미치는 입력 인자들에 관한 영향을 간략히 분석하여 지반과 말뚝 간의 상호작용 분석에 DEM 모델의 실효성을 검증하였다. 이러한 연구를 통해 개단말뚝의 관입 과정 중 변화하는 관내토에 대한 이해를 높이고, 나아가 현장에서의 시공 효율성을 향상시키는 데 기여할 수 있을 것으로 기대된다.
2. 실내모형시험
이 장에서는 수치해석결과와의 검증을 위한 저자가 수행한 실내 모형말뚝시험(Kim et al., 2023) 내용에 관한 내용 즉, 1) 시료 및 지반 조성, 2) 실험장치 및 방법, 3) 실험결과를 소개한다.
2.1 재료 및 시료 조성
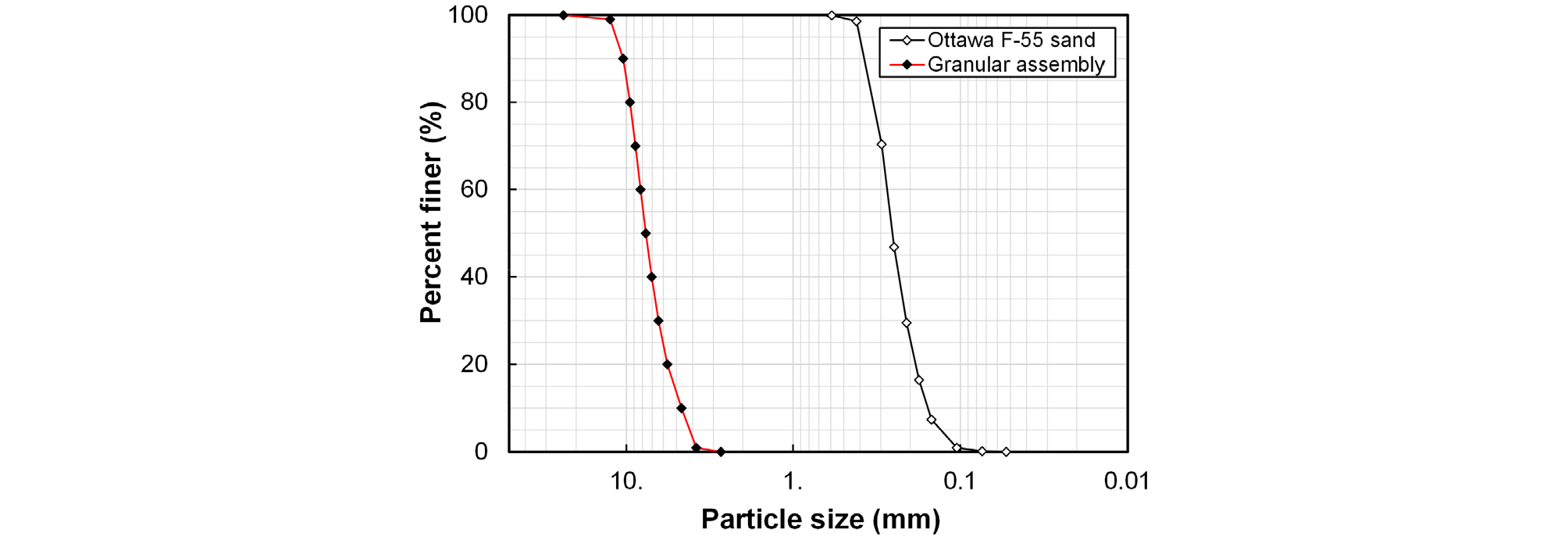
실험 재료로는 Ottawa F-55 모래를 사용하여 모형말뚝시험을 수행할 지반을 조성하였다. 해당 시료에 대한 입도분포곡선은 Fig. 2와 같으며, 입자 크기는 0.1mm에서 0.4mm 사이에 분포하고 평균입경(D50)은 0.256mm이다. 또한, 균등계수(Cu)는 1.76, 곡률계수(Cc)는 1.03에 해당하며 최소, 최대 간극비(emin, emax)는 각각 0.47과 0.78이다. 한계상태 내부마찰각(φc)은 32.8°로 측정되었으며 통일분류법(USCS) 기준에 따라 SP(poorly graded sand)로 분류된다. Table 1은 시험재료에 관한 자세한 물성값을 정리한 표이다.
Table 1.
Engineering properties of Ottawa F-55 sand (modified from Kim et al., 2023)
시료 조성은 건조낙사법을 통해 두께 12.7mm의 각 변의 길이 1219.2mm인 정육면체 형태의 토조에 일정한 유입량을 유지하기 위해 상부에 6번 체(개구부 직경 3.35mm), 하부에 16번 체(개구부 직경 1.18mm)를 결합한 분산체를 활용하여 모래를 통과시켜 균일한 상태의 시료를 조성하였다. 토조 내부에 그 높이와 위치를 달리하며 총 15개의 서로 다른 지점에서 상대밀도(Dr)를 각각 측정하였고 그 결과는 80±1.5%로 확인되어 시료의 균질성을 검증하였다.
2.2 실험장치 및 방법
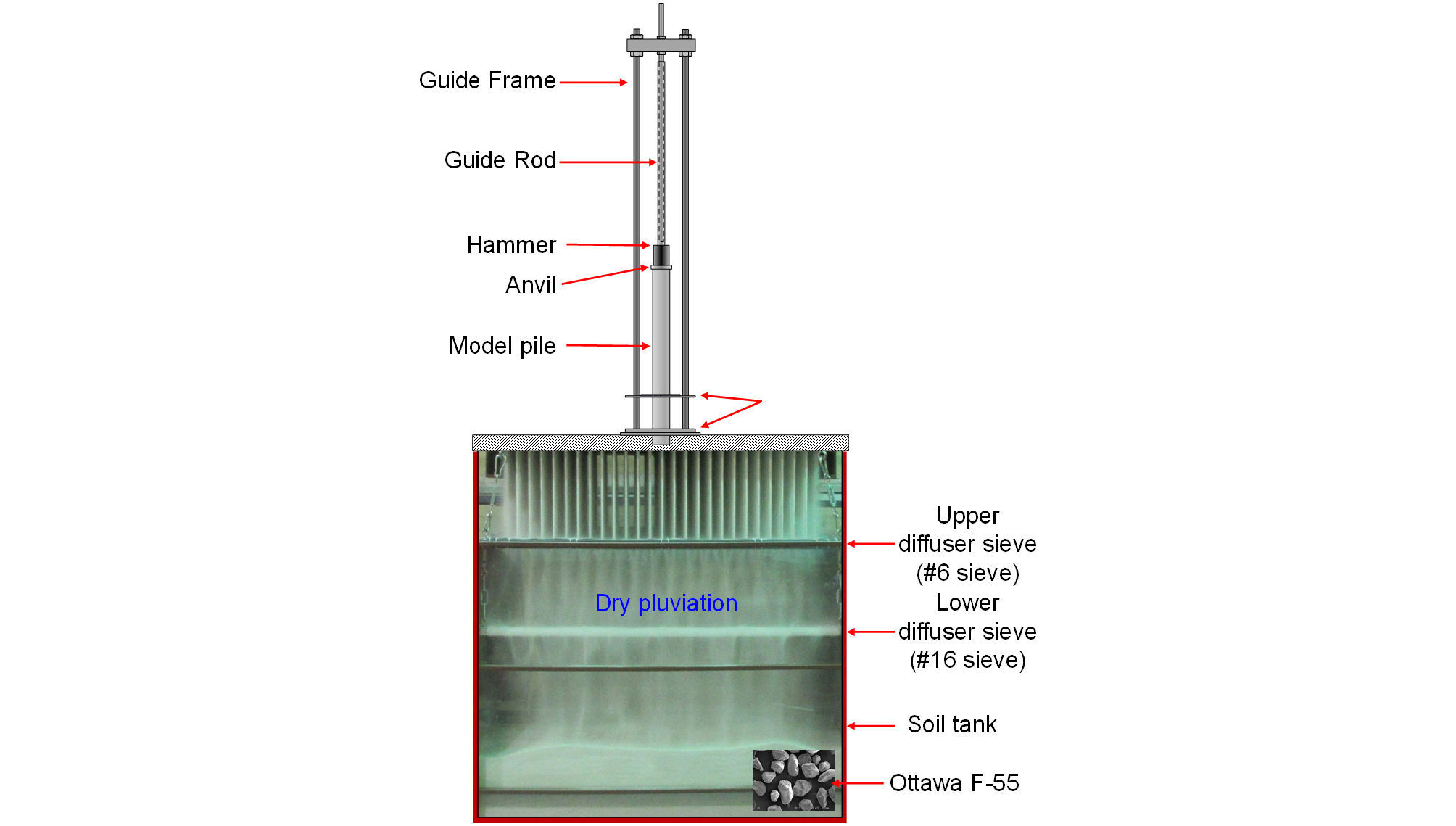
모형말뚝은 외경 88.9mm, 내경 49.3mm 그리고 길이 1114.4mm의 강철 말뚝을 사용했으며 항타에는 해머, 앤빌, 해머 가이드 롯드, 말뚝 가이드 판으로 구성된 항타시스템을 이용하였다(Fig. 3 참조). 말뚝 항타는 8kg의 해머를 800mm의 높이에서 낙하시켜 62.8N·m의 항타에너지로 말뚝을 관입하였고, 이 과정에서 최종 관입 깊이 670mm에 이르기까지 타수에 따른 말뚝의 관입 깊이와 관내토의 길이를 레이저측정기를 이용하여 측정하였다.
2.3 실내모형실험 결과
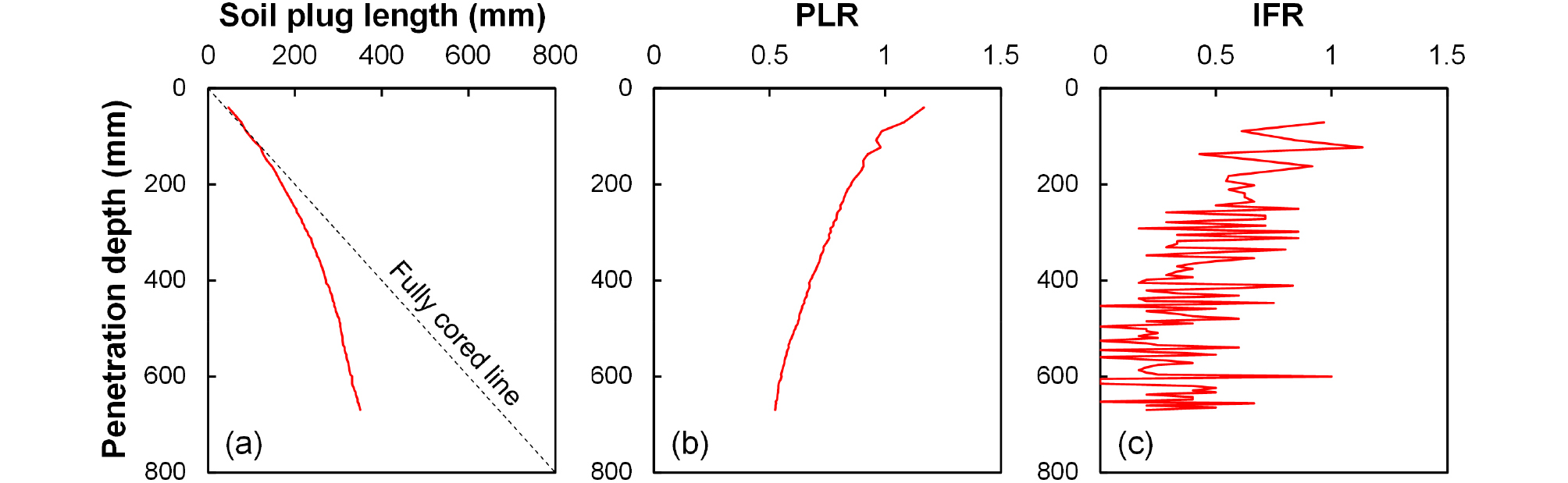
Fig. 4는 모형말뚝시험을 통해 획득한 말뚝 관입 깊이에 따른 관내토 길이 그리고 관내토 상태를 알려주는 길이 지표인 PLR과 IFR 결과이다. Fig. 4(a)에서 알 수 있듯이 항타 초기에 관내토는 관내 아무런 저항 없이 관입되기 시작하여 관입이 진행될수록 내주면 마찰력의 증가로 관내토 길이 증가율이 감소하였다. 말뚝 최종 관입깊이 670mm에서 최종 관내토 길이는 350.7mm로 측정되었고, PLR과 IFR은 각각 0.52와 0.20으로 평가되었다.
3. DEM을 활용한 수치해석
수치해석적으로 개단말뚝의 관입 단계별 관내토 거동의 분석을 위하여 이산요소해석(Discrete Element Method, DEM) 상용 프로그램인 PFC2D(Itasca, Ver. 6.0)를 활용하였다. 이장에서는 입상 재료 생성 및 상대밀도 조절 방법 그리고 말뚝 관입 과정의 모델링 방법을 자세히 설명하였다.
3.1 시료 조성 방법
3.1.1 입상 재료 생성
PFC2D에서는 입자들을 2차원 공간에 원 모양의 개별 요소로 생성할 수 있고, 그 입도분포는 흙 모사체의 거동에 중대한 영향을 미친다고 알려져 있다(Ciantia et al., 2017). 따라서, Ottawa F-55 모래의 입도분포를 모사하여 원형의 입자들을 생성하여야 하지만 실제 입자 크기대로 모사하게 되면 입자 수가 기하급수적으로 증가하여 비현실적인 해석 시간이 소요되므로 응력 분석을 목표로 하는 기존 문헌에서는 일반적으로 실제 시료의 입경을 10배 이상 확대하여 생성하고 있다(Li et al., 2021). 이에 본 연구에서는 모델 수립 초기 과정의 시행착오를 포함하여, 다양한 종류의 입력 인자를 조절하며 반복적인 모델링 과정을 소개하고자 했기 때문에 실제 입경에 30배 확대하여 흙 입자를 생성하였다(Fig. 2 참조).
3.1.2 시료의 상대밀도 조절 방법
각 요소는 입자 간의 접촉(Contact)을 형성하며 그 접촉에 부여된 접촉모델(Contact model)을 기반으로 모델 전체의 거동이 계산되므로 접촉모델의 선정은 매우 중요하다. 보편적으로 이용되던 기존의 선형모델(Linear model)의 경우, 마찰계수를 아무리 높게 설정하여도 내부마찰각이 25° 이상 구현되지 않거나 해석에 따른 입자의 회전각이 실제보다 과다하게 도출되는 문제점을 안고 있다(Li et al., 2019). 이는 DEM 해석상 원형 요소는 요철을 포함한 실제 흙 입자의 모양을 반영하지 못하기 때문으로 알려져 있고, 이를 극복하기 위해 Rolling Resistance Linear Model(RRLM)이 개발되었다. 이 모델은 기존의 선형모델에 태엽과 같은 회전저항력을 부여함으로써 입자의 모양에 의한 효과를 반영한다.
PFC를 활용한 수치해석에 있어 입상 재료의 전단거동은 물리적 실험에서와 같이 팩킹 상태(Packing state)에 크게 의존한다. 기존 연구들에 의하면 DEM에서 지반의 전단거동을 조절하기 위하여 팩킹 상태를 조절할 때 간극비나 간극률 대신 상대밀도를 통하여 조절할 것을 권고하고 있다(Salot et al., 2009). 상대밀도를 정의하기 위해서는 최대, 최소간극비가 필요한데 2차원 수치해석 상에서는 이를 측정하기 위한 실험적 방법을 적용하는 데 한계가 있으므로 수치해석적인 측정 기준을 제시하여 후속 연구들에서 널리 사용되고 있다(Muir Wood and Maeda, 2008; Salot et al., 2009).
본 연구에서는 Muir Wood and Maeda(2008)가 제시한 일련의 과정을 Fig. 5와 같이 개선하여 활용함으로써 극한 간극비를 측정하였다. 해당 방법은 2차원 DEM 해석상에서 초기 상대밀도를 조절하여 샘플을 조성할 수 있도록 하는 수치해석적 방법으로, 크게 네 단계로 구성되어 있다. 먼저, 최소간극비를 측정할 경우, 부재(Wall) 요소로 둘러싸인 직사각형 공간(Cell) 내에 10%의 간극률을 만족하도록 입자들을 생성한다. 이때 초기 조성 상태는 굉장히 낮은 간극률로 인해 입자들이 비현실적으로 압축되어 각 부재에는 내부로부터의 엄청난 응력이 측정된다. 따라서, 이 팩킹 상태의 완화를 거쳐 최소간극비 상태까지 도달하기 위해, 입자 간 선형마찰계수와 굴림마찰계수를 모두 ‘0’으로 고정한 상태에서 각 부재 요소를 바깥 방향으로 이동시켜 셀을 팽창시킨다. 이 과정에서 셀 내부 샘플의 등방압축상태가 유지되도록 부재를 이동하여야 하며 특히, 해당 응력(σm0=kn×10-4)값으로 Normal stiffness(kn)의 10-4배로 사용할 것을 권고하고 있다. 접촉 모델의 입력 인자 중 Normal stiffness(kn)와 Shear stiffness(ks)는 이축압축시험을 통하여 실제 모래와 같이 거동하도록 보정되어야 한다.
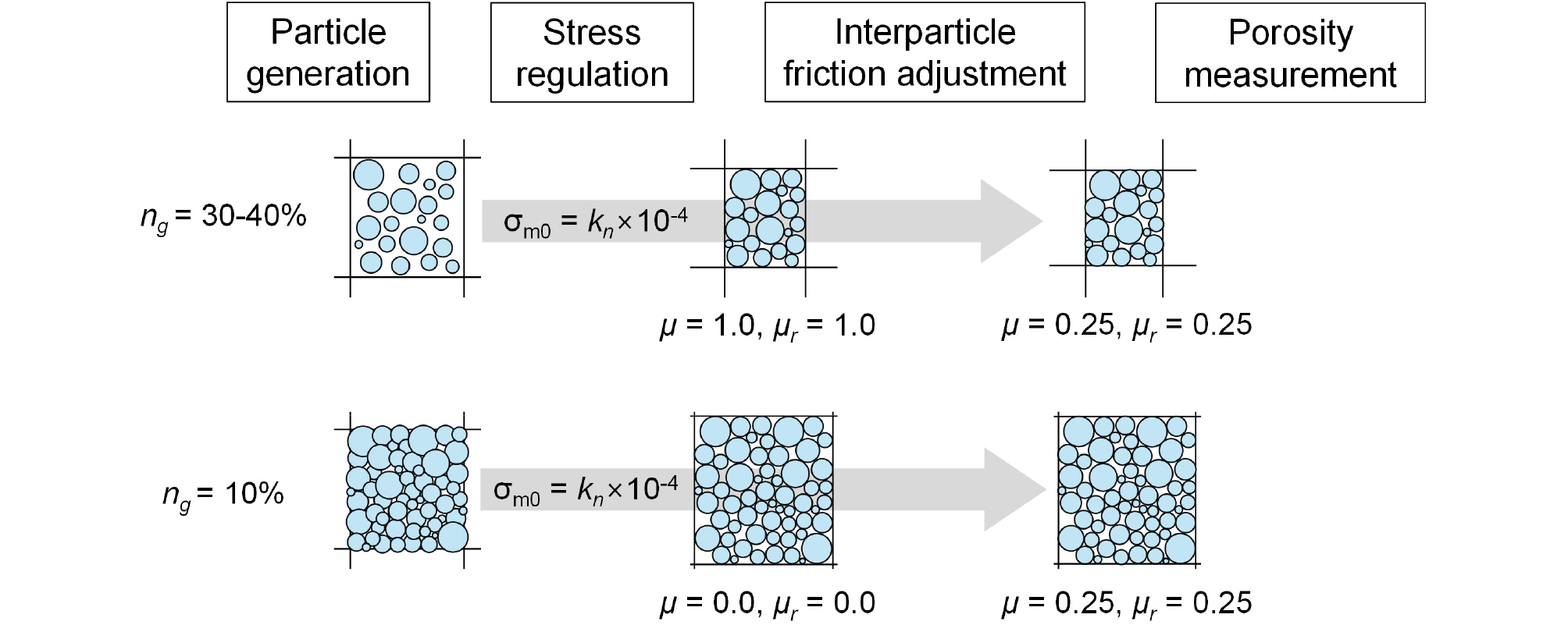
Fig. 5
Procedure of the determination of minimum and maximum porosity (modified from Muir Wood and Maeda, 2008)
이렇게 조성된 시료에서 최종적으로 두 마찰계수를 모두 0.25로 변경한 후, 응력(σm0)이 유지되도록 부재의 위치를 조절하며 새로운 평형상태까지 해석하여, 이때 셀 내의 간극비를 최소간극비로 정의하였다. 최대간극비의 경우 초기 조성 간극률을 30-40%로 설정하며 이를 응력(σm0)까지 초기 압축시키는 과정 직전에 마찰계수들을 ‘0’이 아닌 ‘1.0’으로로 변경한다는 점을 제외한 모든 과정은 동일하다.
3.2 시료의 전단거동 검증 및 시료 조성 조건
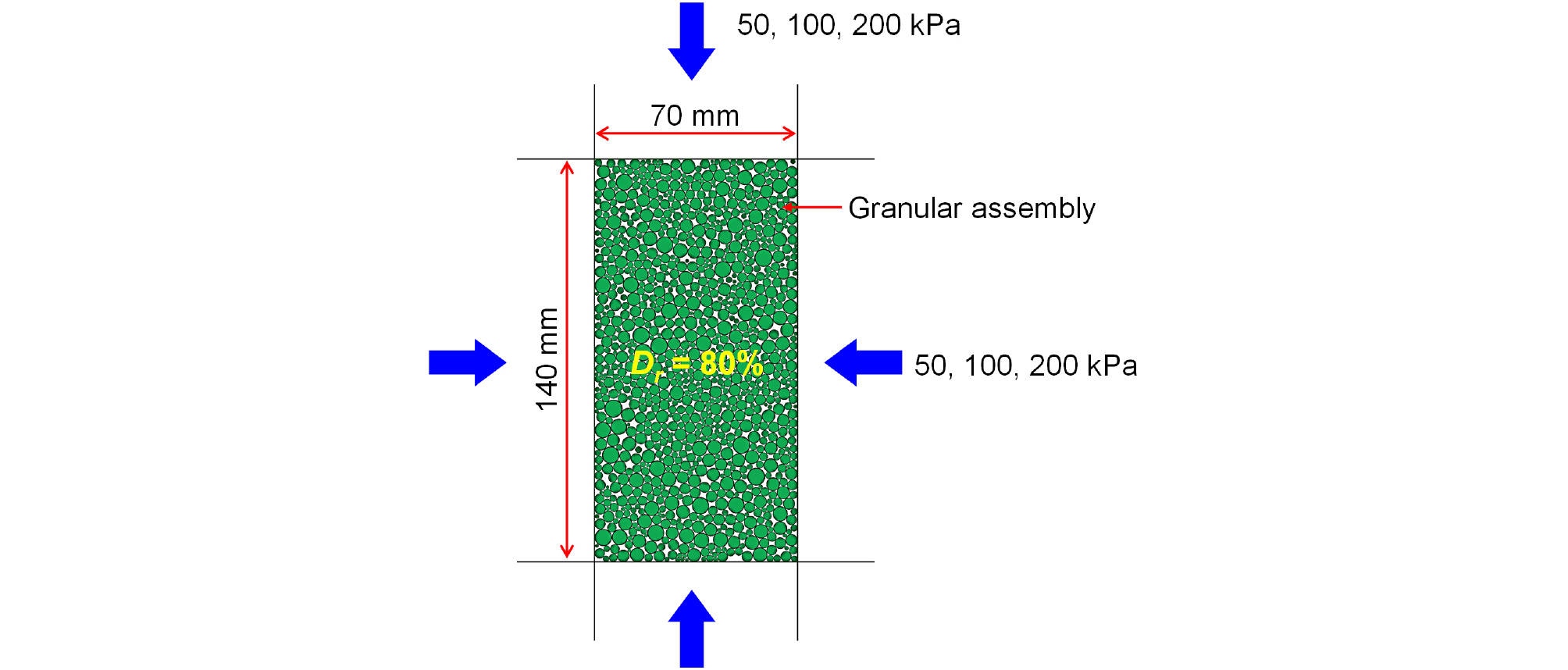
앞서 설명한 것과 같이 생성한 입자를 실내모형시험에 규격에 맞춰 시료를 조성하기 전에 접촉 모델의 입력값(즉, kn와 ks) 결정을 위해 DEM 상에서 이축압축시험(Biaxial Compression Test)를 수행하였다. 이 이축 셀은 앞서 측정한 극한 간극률을 토대로 상대밀도 80%로 시료가 조성되었으며, 그 결과는 Fig. 6과 같다. 이 셀은 각각 등방압축응력 50kPa, 100kPa, 200kPa 하에서 축방향 변형률이 20%에 도달할 때까지 축차응력이 가하여 첨두내부마찰각(Peak friction angle, φp)을 평가하였다. Table 2는 접촉 모델의 입력값을 포함한 PFC 입력값을 정리한 표이다.
Table 2.
Value of input parameters for PFC2D
Itasca 사에 의하면 DEM 상에서 입상 재료의 시료를 조성할 때, 특정 공간 내에 원하는 최종 간극률대로 입자를 생성하는 것만으로는 간극률을 조절하면서 동시에 응력과 간극비 면에서 균질한 지반을 조성하기는 불가능하다(Itasca, 2021). 이에 마찰계수를 조절하며 특정한 과정을 거치는 시료 조성법이 필요하다(Esposito et al., 2018).
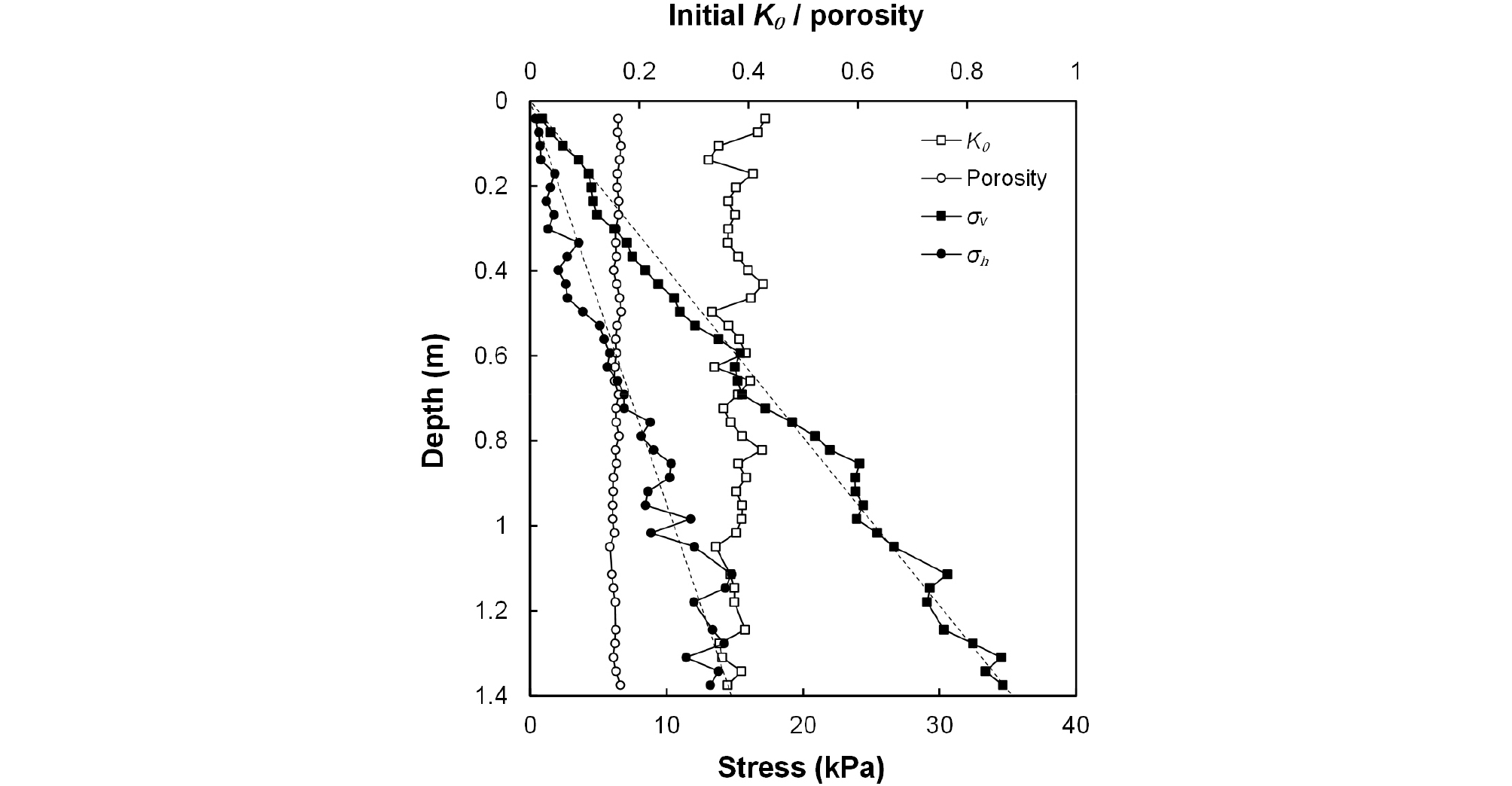
따라서, 본 연구에서 사용한 지반 조성법은 PFC 모델상의 토조의 각 변을 최종 샘플의 크기보다 10% 이내의 비율로 확대하여 생성한 후, 그 내부에 마찰이 없는 상태의 입자들을 목표 간극률 보다 10% 이내의 비율로 크게 설정하여 생성하였다. 이렇게 느슨하게 생성된 시료를 입자 간의 접촉이 모두 사라질 때까지 평형해석을 수행한 후, 접촉 모델의 마찰력을 부여하고 토조의 형성하는 네 변을 최종 샘플의 크기가 되도록 서서히 이동시켜 시료를 압축하였다. 토조의 크기와 입자 생성 간극률의 확대 비율을 조정하며 여기까지의 과정을 반복적으로 수행하였다. 토조의 크기와 시료의 간극률 모두 목표값에 도달함을 확인하여 시료 조성을 완료하였다. 시료 조성 완료 후 시료의 상태는 0.16의 간극률과 0.4의 토압계수로 균일한 시료를 조성하였고, Fig. 7은 깊이에 따른 간극률, 토압계수, 각 방향 응력 상태를 도시한 그래프이다.
3.3 말뚝 관입의 모델링
모사된 시료에 말뚝의 항타 관입 과정을 모사할 경우 말뚝의 물성, 말뚝과 입자 간의 상호작용 역시 관내토 형성과 그 거동에 큰 영향을 미친다. 본 연구에서는 말뚝 항타 과정의 수치해석결과와 실내모형시험 결과의 비교를 통해 수치해석 입력값들을 결정하고 말뚝과 입자 간의 상호작용을 검증하였다. 또한, 수치해석 시 말뚝의 관입 방법을 소개하고 관입 속도에 따른 관내토 거동에 미치는 영향을 분석하였다.
항타를 모사하는 수치해석의 경우 항타 수에 의한 말뚝의 변위 변화를 모사하는 방식은 크게 두 가지로 분류할 수 있다. 첫 번째 방법은 ‘재하법’으로 말뚝을 지반 표면에 접촉시킨 뒤 연직방향으로 일정한 힘을 재하하여 말뚝을 관입하고 평형상태를 이룰 때까지 해석하는 과정을 매 타수마다 반복하는 방법이다(Liu et al., 2019). 해당 기법은 말뚝을 구성할 때 부재(Wall)가 아닌 입자(Ball) 요소를 촘촘히 겹쳐 구성하는 등의 보조적인 방법이 필요하다. 두 번째 방법은 ‘변위조절법’으로 부재 요소로 구성된 말뚝의 위치를 관입 속도를 조절하여 관입시키는 방법으로써 실제 말뚝 관입 과정과 동일한 모사가 가능하다(Liu et al., 2019; Li et al., 2021). 따라서, 본 연구에서는 보조적인 기법이 필요 없는 변위조절법을 채택하여 말뚝 관입 과정을 모사하였다.
수치해석에서 조절한 말뚝의 변위는 해석 시간의 효율성을 위해 실제 96타수의 항타 기록을 8타씩 묶어 총 12타로 구성하였다. 또한, 말뚝의 변위를 조절할 때 시간에 대해 각 요소의 거동을 계산하는 DEM의 특성상 말뚝 부재에 일정한 시간 동안 실제 모형시험결과를 반영한 특정 변위를 부여하여 관입을 모사하였다.
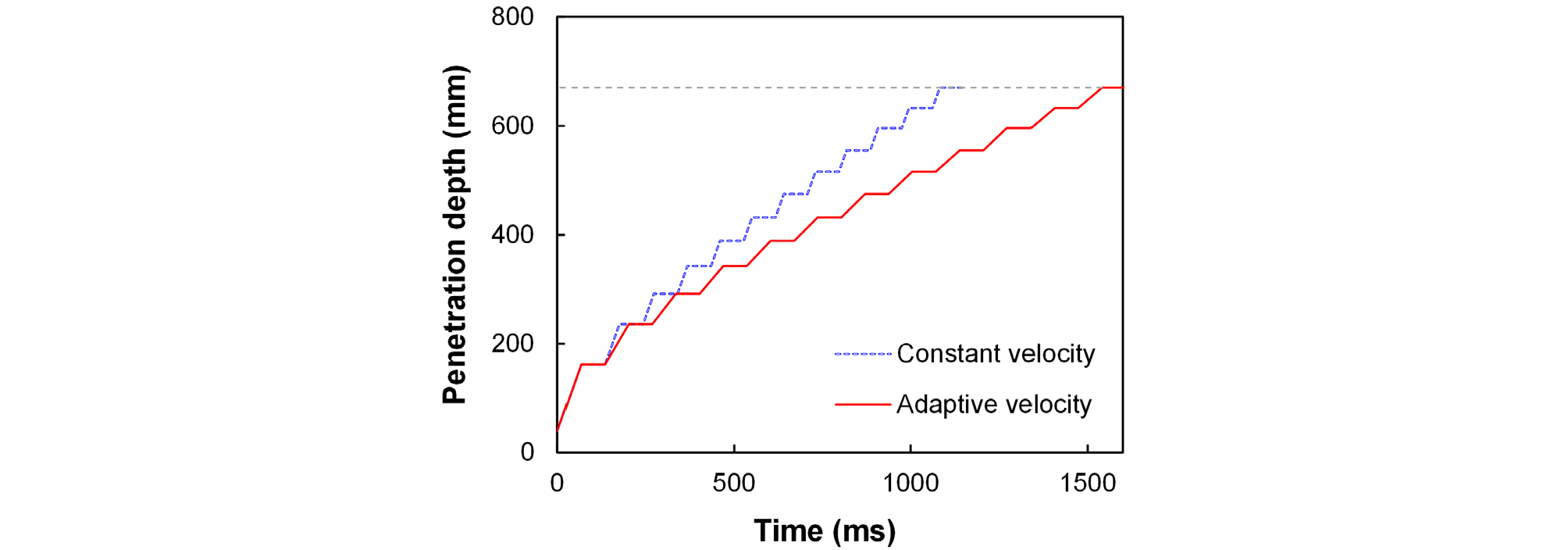
불연속적인 관입을 유발하는 항타의 상황을 물리적으로 모사하기 위해서는 말뚝을 각 타수에 의한 변위만큼 이동시킨 후에 이를 정지시킨 상태에서의 평형해석이 필수적이다. 이때, 실제 모형말뚝시험에서 말뚝과 항타기의 접촉시간이 일정하다는 가정하에, 각 타수당 말뚝의 변위가 최종 관입깊이에 가까워질수록 점차 감소하는 현상을 반영하기 위해 모든 타수에 대해 일정한 관입 속도(Constant velocity)를 적용하는 대신 타수가 거듭됨에 따라 관입 속도를 점차 느리게 조절하는 적응형 속도(Adaptive velocity)를 적용하였다(Fig. 8 참조). 다음으로는 관내토의 압축 거동을 효과적으로 모사하는 적응형 속도 방식에서 초기 속도의 영향을 분석하여 초기 속도를 1.8m/s로 결정하여 해석을 수행하였다.
4. 모델링 분석 결과 및 수치해석결과 비교
4.1 흙 입자 간의 상호작용 검증
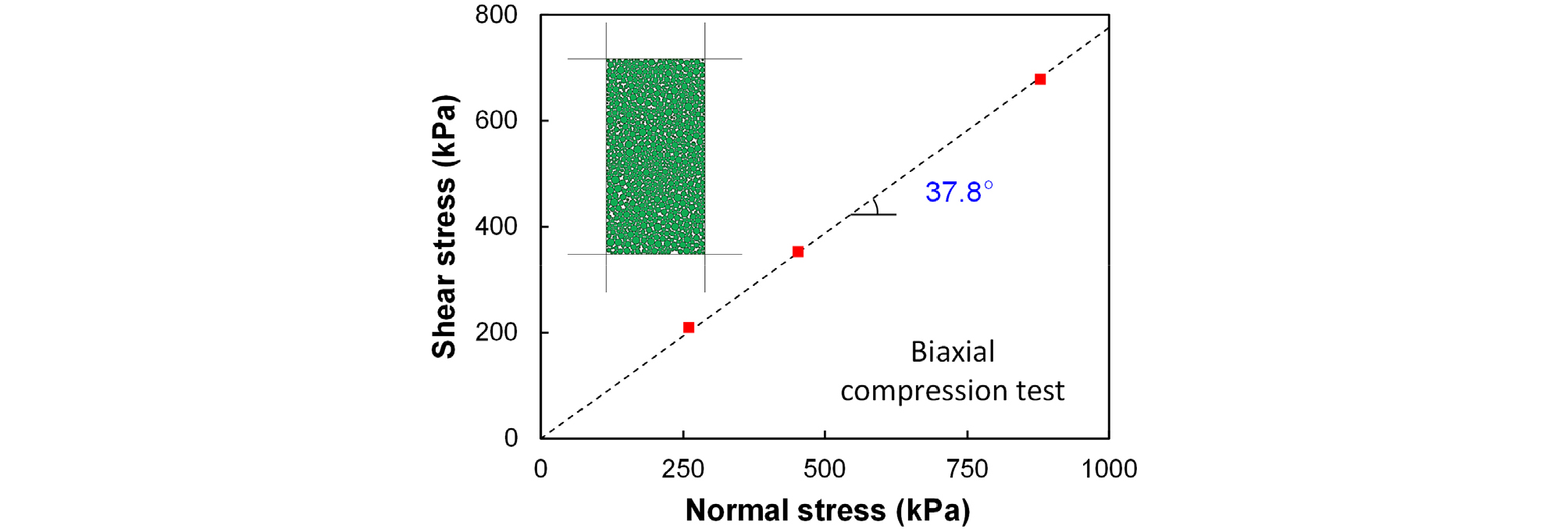
실내모형시험 주시료인 Ottawa F-55를 모사하여 생성한 입상 재료가 실제 시료와 동일한 전단거동 특성을 보이는지 검증하기 위해 PFC2D에서 실행한 이축압축시험의 과정과 결과는 다음과 같다. 입상 재료를 사용해 이축압축 시료를 준비하여 등방압축응력을 증가시키며 축방향 변형률이 20%가 될 때까지 전단 과정을 접촉모델의 입력값들을 조절하며 반복하였다. 그 결과 Table 2와 같이 입력값들을 결정할 수 있었으며, 결정된 입력값으로 설정 후 이축압축시험을 진행한 결과, Fig. 9와 같이 37.8°의 첨두내부마찰각이 평가되었다. 이는 실제 Ottata F-55를 사용한 실험 결과값인 38°와 비교하여 평균절대오차 0.5%의 차이를 보였으며, 결정된 입력값들의 설정으로 구현한 입상 재료의 접촉 모델이 Ottawa F-55 시료의 전단거동이 정확히 모사되었다고 판단된다.
4.2 초기 관입 속도의 영향
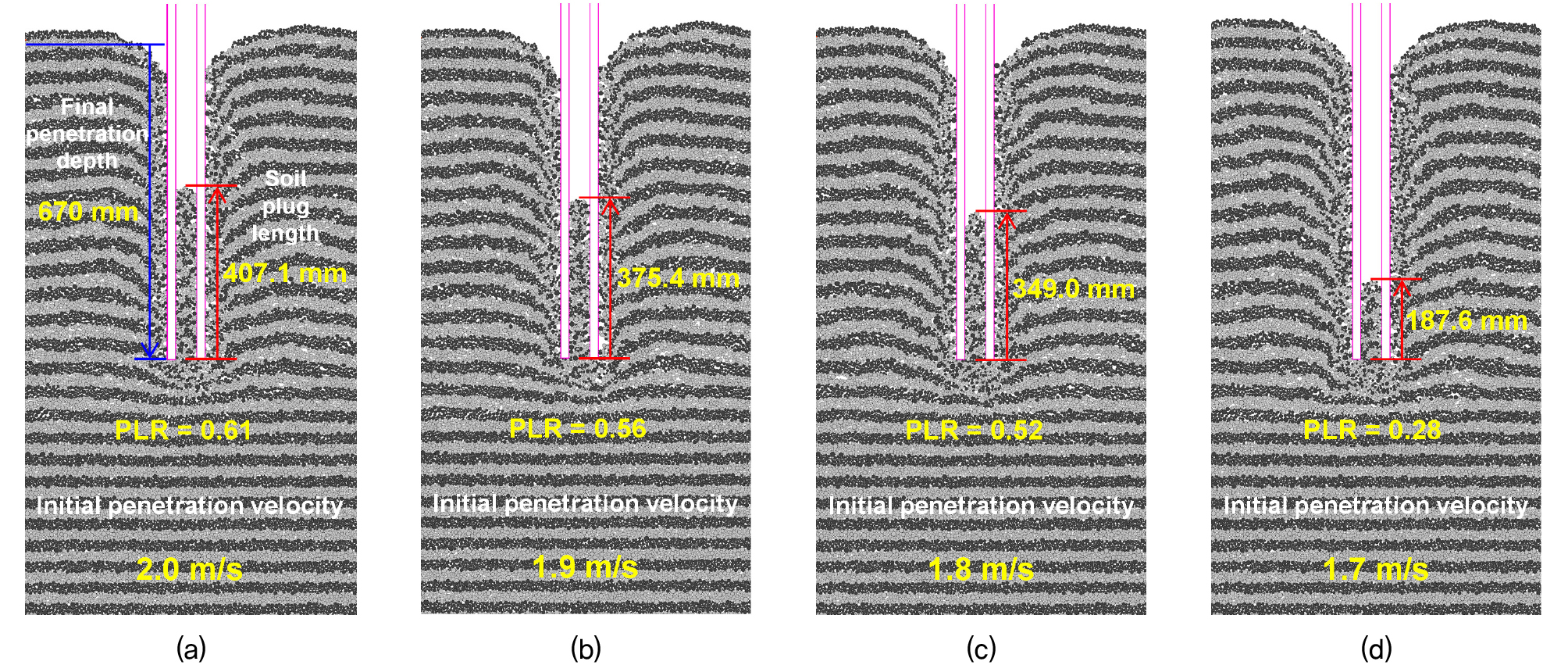
3.3절에서 설명한 것과 같이 말뚝 관입에 적응형 속도 방식을 적용하여 변위를 조절하였을 때 관내토의 압축 거동이 가장 효과적으로 모사되었다. 이 조건에서 초기 관입 속도의 영향을 분석하기 위해 초기 관입 속도를 2m/s, 1.9m/s, 1.8m/s, 1.6m/s로 변화시켜 말뚝을 관입시키는 해석을 진행하였고 Fig. 10은 각 경우에 대하여 해석이 최종 완료된 모습을 나타낸 그림이다. 또한, 최종 관입 상태로부터 측정된 관내토의 길이는 2.0m/s의 경우부터 1.6m/s까지 차례대로 407.1mm, 375.4mm, 349.0mm, 187.6mm로 확인되었으며, 이로부터 PLR을 계산한 결과는 각각 0.61, 0.56, 0.52, 0.28이었다. 초기 속도의 크기가 작을수록 관내토의 길이는 짧게 나타나 작은 PLR 값을 보였으며 그 정도는 초기 속도가 작을수록 크게 관찰되었다. 이는 관입 속도가 작을수록 항타에서부터 압입에 가까워지는 거동을 모사하기 때문으로 해석되며, 초기 관입 속도 1.8m/s의 경우, 모형말뚝시험의 최종 관입 깊이 670mm에서 형성된 최종 관내토 길이인 350.7mm와 0.48%의 절대오차를 보였다.
4.3 수치해석과 실내모형시험의 결과 비교
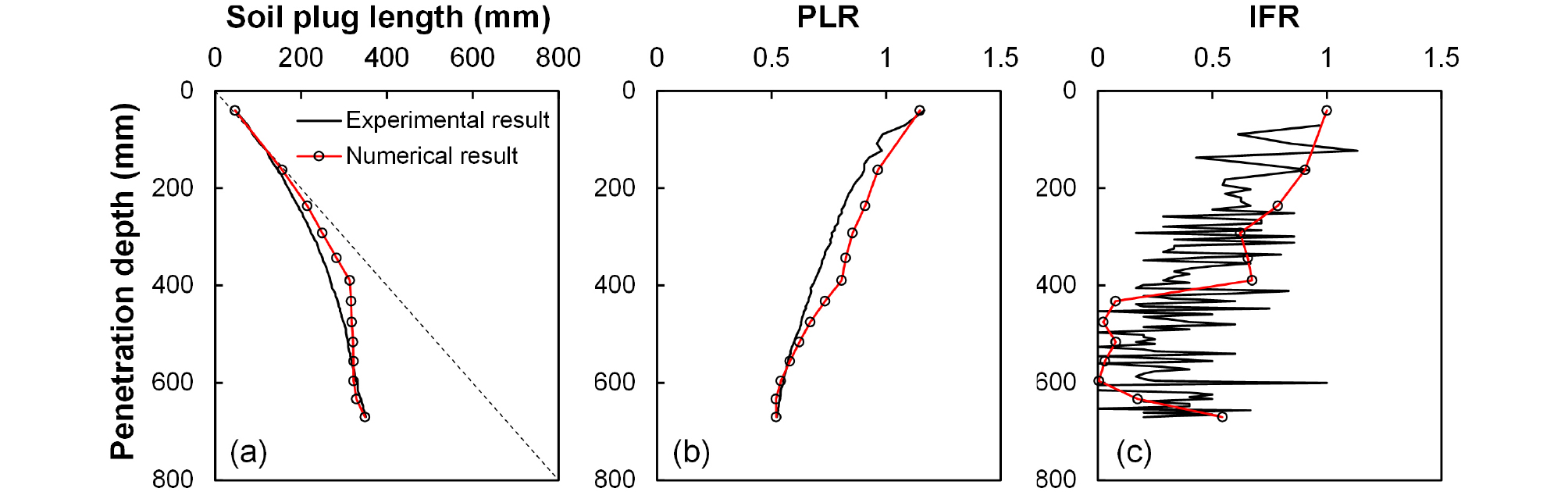
Fig. 11은 개단말뚝의 항타 과정을 분석한 수치해석 모델의 검증을 위해 관내토 길이 면에서 모형말뚝 실험 결과와 비교한 그래프이다. DEM 상에서 말뚝이 최종 관입 깊이 670mm까지 관입되는 모든 과정 동안 말뚝 내부에 형성되는 관내토 길이를 측정하였고, Fig. 11(a)는 이를 관입 깊이에 대해 도시하여 실제 모형실험의 결과와 비교한 그래프이다. 수치해석 결과 최종 관입 상태에서 관내토의 길이는 349.0mm로 측정되었고, 항타 전 과정에 걸쳐 관내토 길이를 실험치인 350.7mm에 맞춤으로써 이산요소해석법을 활용한 개단말뚝의 관내토 거동 분석의 가능성을 검증하였다. 더불어 항타 모사 전 과정에서 관입 단계별 관내토 길이로부터 PLR과 IFR을 평가하여 수치해석 결과의 신뢰성을 확인할 수 있었다(Fig. 11(b)와 11(c) 참조). PLR의 경우 첫 항타 직후 실험 데이터와 같이 1보다 큰 값을 나타내는데, 이는 상대밀도 80%로 압축되었던 표층 부근의 지반이 해당 단계에서 말뚝 관입에 의해 교란되며 부피가 일시적으로 커졌기 때문이다. 이어서 초기 관입이 진행됨에 따라 PLR은 말뚝이 292mm까지 관입된 시점에서 0.85가 될 때까지 급격하게 감소하며, 이후 관입 과정에서는 그 감소량이 적어져 최종 관입 깊이에서는 0.52를 나타낸다. 이 경향은 Fig. 11(b)의 실험 측정치 추세와 동일하여 이산요소법을 활용하여 관내토의 상태까지 성공적으로 모사되었다고 판단된다. 또한, Fig. 11(c)에서 볼 수 있듯 IFR은 모형실험이나 수치해석의 경우 모두 PLR에 비하여 변동성이 크지만, 공통적으로 1의 값에서 시작하여 관입이 진행될수록 점차 감소함을 알 수 있으며 대부분의 구간에서 등락의 폭 또한 일치함을 확인하여, PFC 수치해석 상 개단말뚝의 관내토 거동이 잘 반영되었다고 판단된다.
5. 결 론
본 연구에서는 모형말뚝시험 결과와 수치해석결과의 비교를 통하여 DEM 모델의 검증을 수행하고 개단말뚝과 지반을 DEM 상에서 구현하여 항타 관입 과정을 모사할 수 있는 모델을 개발하였다. 또한, 이를 활용하여 개단말뚝의 항타 과정에 따라 변화하는 관내토의 거동 및 상태를 분석하였고, 수치해석 상 초기 관입 속도의 변화가 관내토 거동에 미치는 영향을 분석하여 도출된 결론은 다음과 같다.
(1) 흙 입자 간의 상호작용 검증 과정에서 입자 간 회전저항력이 고려되는 Rolling Resistance Linear Model(RRLM)을 적용하고 수치해석 입력 인자들을 조절한 결과 최종 입력값을 결정할 수 있었고, 최종 입력값을 반영한 이축압축시험을 수행한 결과 입상 재료의 첨두내부마찰각은 37.8°로 평가되었다. 결론적으로 모형시험재료인 Ottawa F-55 모래의 첨두내부마찰각과 일치시킴으로써 흙 입자 간의 상호작용이 검증되었다.
(2) 2차원상의 원형 입상재료(Granular assembly)의 상대밀도(Dr)를 조절할 수 있는 기법을 적용하고 관내토의 압축 거동을 성공적으로 모사하기 위해 가장 중요한 요인인 말뚝의 속도를 제어하는 ‘변위조절법’을 활용하였다. 그 중에서도 해머와 말뚝 사이의 항타 순간의 접촉시간을 일정하다고 가정하여 항타가 거듭됨에 따라 관입 속도를 점점 감소시키는 ‘적응형 속도’를 적용하여 모형실험에서의 관내토 압축 거동을 모사하였다.
(3) 추가적으로 해당 방식에 대하여, 말뚝의 초기 관입 속도가 관내토 거동에 미치는 영향을 분석한 결과 초기 관입 속도가 감소할수록 관내토가 더 압축되는 경향을 확인할 수 있었다. 입상 재료 접촉 모델의 입력값과 더불어 초기 관입 속도가 관내토 거동에 큰 영향을 미쳤다.
(4) 실험적 한계로 인해 직접 측정하기 어려운 개단말뚝 내 관내토의 상태 변화를 분석하기 위해 항타 전 과정을 DEM 모델로 구현할 수 있었다. 이산요소해석법 통해 항타 과정에 따라 형성되는 관내토의 길이는 최종 관입 깊이 670mm에서 349mm로 평가되었으며, 이는 모형말뚝시험 결과인 350.7mm에 가까운 수치였다. 또한, 이산요소해석을 통해 획득한 관내토 상태를 나타내는 대표적 지표인 PLR과 IFR 값은 각각 0.52와 0.54였다. PLR 값 0.52는 모형말뚝시험 결과와 같았지만, IFR 값은 최종 관입 깊이에서 0.54로 평가되어 실험 결과값인 0.30와 차이를 보였다. 하지만, IFR은 PLR과 달리 그 변동성이 커 차이를 보였지만, 관입 깊이가 깊어질수록 IFR 값이 감소하는 경향은 일치하였다.
향후 DEM을 이용하여 개단말뚝의 관내토 거동을 연구하는 과정에서 발생할 수 있는 시행착오를 최소화하고자 본 연구에서는 DEM 모델 개발 과정과 개발 모델의 검증 과정을 소개하였고, 본 연구를 통해 도출된 결과는 관내토의 거동을 분석함에 있어서 관내토 폐색상태를 간접적인 지표인 관내토 길이가 아닌 내부 상태를 직접 반영하여 관내토의 거동을 분석하는 향후 연구에 기여할 것으로 판단된다.