1. 서 론
1.1 연구 범위 및 목표
2. 터널 라이닝 모형시험체 제작 및 GPR 시험
3. 수치모델링
3.1 구성방정식
3.2 재료 물성 및 GPR 안테나 제원
4. 결과 및 분석
4.1 수치해석 결과 및 검증
4.2 라이닝 두께, 방수막의 영향
5. 결 론
1. 서 론
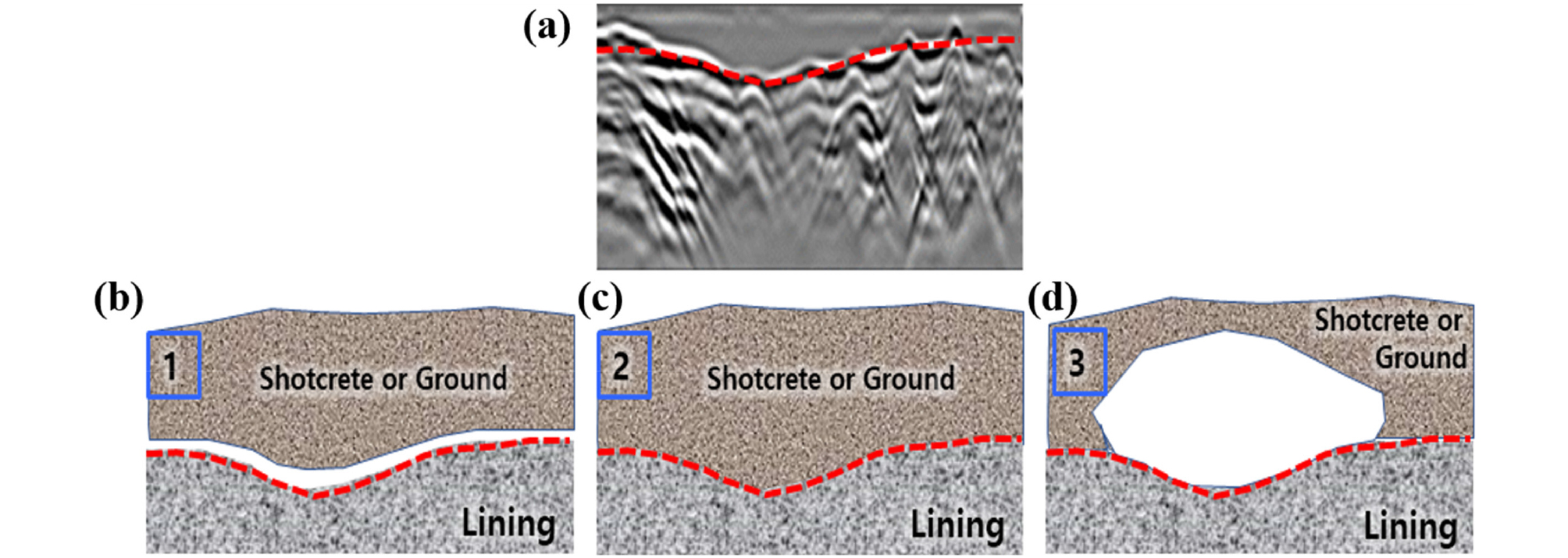
터널은 철도, 도로, 수로 등 여러 목적으로 건설되어 운영되고 있으며, 갈수록 노후화되고 개량을 필요로 하는 터널도 급격히 증가하고 있어 터널 구조물의 안전 확보를 위한 상태 점검 및 진단 기술 개발의 중요성이 커지고 있다. 노후화된 터널은 건설 당시부터, 운영 중에 누수, 균열, 공동, 지진 등 다양한 위험 요인에 노출되며 그 위험도는 증가된다. 이 중 터널 라이닝 내부 및 배면에 존재하는 공동(Cavity)은 다양한 원인에 의해 발생될 수 있으나, 대부분의 경우 육안검사가 불가능한 곳에 존재하기 때문에 이에 대한 점검이 쉽지 않다. 현재는 Fig. 1(a)와 같이 코어링(Coring)에 의존하여 터널 라이닝 두께를 검측하고 있다. 하지만 코어링은 구조물에 손상을 주며, 검측에 많은 시간이 소요될 뿐만 아니라 특정 지점만 조사가 가능하다는 한계점이 있다. 따라서, 최근에는 GPR(Ground Penetration Radar)과 같은 비파괴시험 등을 이용한 터널 라이닝과 배면에 대한 상태를 평가하는 시도가 이루어지고 있다(Fig. 1(b)). GPR은 지반 내 공동과 같이 유전율 차이가 큰 매질의 탐사 시에 주로 이용되는데(Kim et al., 2000; Hong et al., 2015), 비파과적으로 탐사하기 때문에 터널 구조물에 손상을 가하지 않는다. 또한, 비교적 적은 탐측 시간이 소요되며, 특정지점이 아닌 전 구간에 대해 효율적으로 조사가 가능하다는 장점이 있다.
이러한 이유로 GPR을 활용한 터널 라이닝 및 배면에 대한 탐사 시도와 연구가 증가하고 있는 추세이다. 국외의 경우, Anne et al.(2016)이 터널 라이닝 배면의 공극의 탐사를 위한 여러 GPR 안테나 방식에 대한 시험을 수행하였고 이 중 지면접촉식(Ground-coupled) GPR 안테나가 가장 우수한 적용성 결과를 보인 바 있다. 이 외에도 라이닝 배면 그라우팅 여부 및 두께 탐사(Zhang et al., 2010), 라이닝과 암반의 접촉 상태(Cardarelli et al., 2003), 라이닝 두께(Li et al., 2011), 라이닝 철근 배근 상태 및 위치 탐사(Xiang et al., 2013), 배면 지하수 상태(Li et al., 2010), 철도 터널의 변형 탐사(Zan et al., 2016)를 위한 GPR 적용성 판단 및 데이터 분석 기술에 대한 연구 등이 이루어진 바 있다. GPR 수치해석과 관련해서 Liu et al.(2007)는 유한영역시간차분 해석을 수행하였고, 제안된 해석기법이 GPR 시뮬레이션에 매우 효과적인 도구가 되며 광범위한 분야에 활용될 수 있음을 보여주었다. Feng et al.(2018)은 유한요소시간영역(Finite Element Time Domain)법과 유한차분시간영역(Finite Difference Time Domain)을 결합시킨 새로운 형태의 하이브리드 알고리즘 이용하여 불규칙하고 복잡한 터널 라이닝 결함을 평가하였고, 개발된 모델이 라이닝 배면에 존재하는 균일 및 균열로 인한 누수를 정밀하게 식별함을 확인하였다.
한편, 국내의 경우, Park and Cho(2006)가 철근콘크리트 도로상판과 터널 라이닝 배면의 연속 공동에 대한 모형시험을 수행한 바 있다. Song et al.(2009) 및 Kim et al.(1997)은 터널 라이닝 배면의 공동에 대한 적용가능성을 확인 후 다른 시험법과의 병행을 통해 터널 라이닝의 보다 정확한 평가가 가능하다는 결론을 도출하였다(Lee et al., 2019). GPR 수치해석과 관련해서는 기초모형개발 및 응용연구가 활발해지고 있지만 아직까지는 지반의 공동(Cavity) 탐지에 적용된 사례가 주를 이루고 있다. Cheon(2016)은 도심지 도로 천부의 지하공동 탐지를 위한 GPR 해석연구를 수행한 후 그 신호반응을 실대형 실험결과와 비교분석한 바 있다. Jang et al.(2016)은 GPR 장비의 전자기펄스 방사를 모사하는 3차원 모델을 개발하여 단순화된 공동모델에 대한 GPR 반응을 검토하였고, 개발된 모델이 도심지 도로하부 지하공동의 부존 정보를 얻는데 효과적으로 활용될 수 있음을 확인하였다.
1.1 연구 범위 및 목표
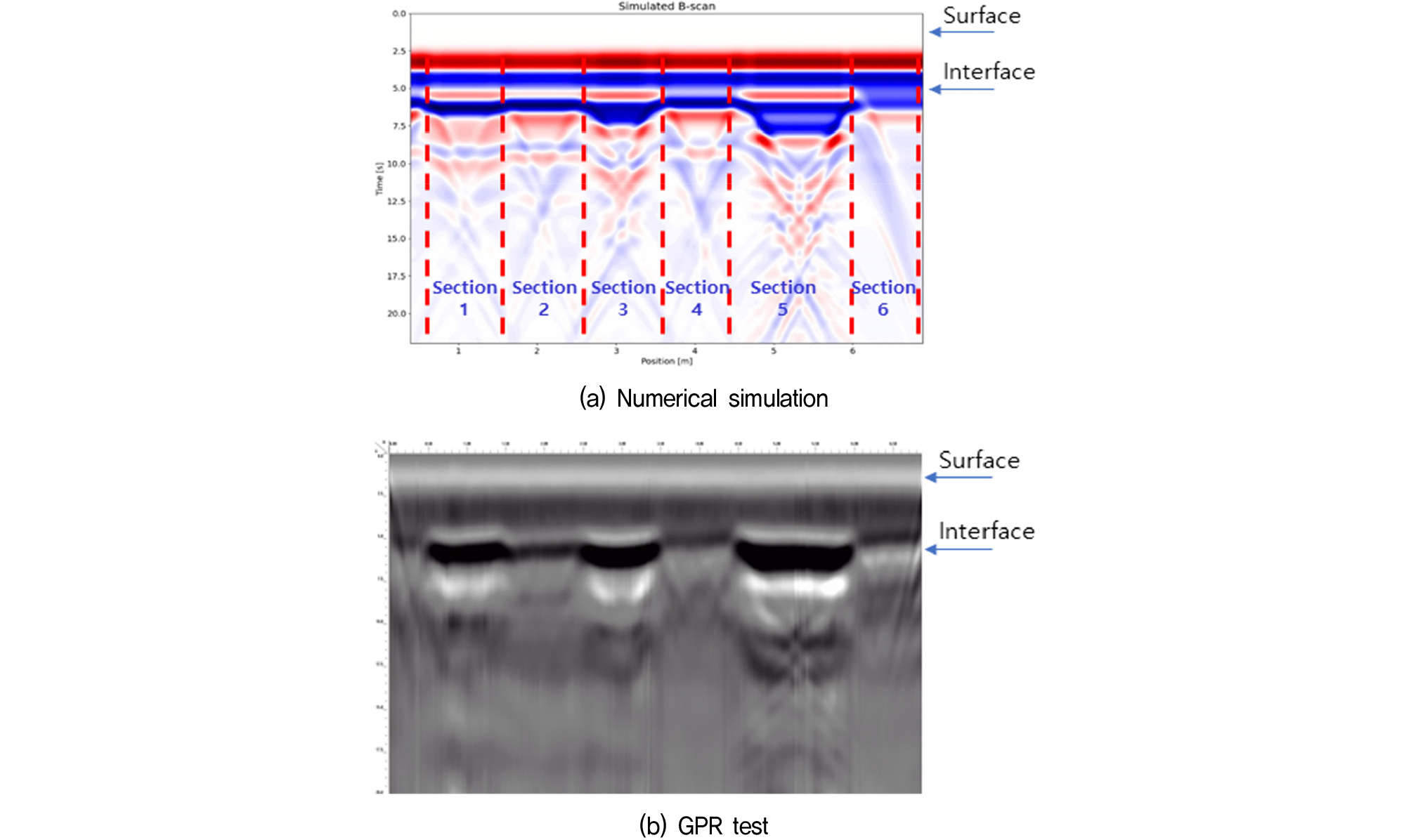
다양한 시공 상태에 대한 GPR 신호의 특성을 파악하고 이를 기준으로 라이닝 및 배면의 상태 분석 기법을 개발하여 현장에 적용하는 것이 시공된 터널 구조물의 면밀한 안전진단을 위해 매우 중요하다. 그러나 현재 터널 라이닝과 배면의 공동 유무 파악 또는 공동의 크기 식별 등을 위한 GPR 신호 분석에는 기술적 어려움이 있다. Fig. 2(a)와 같이 관측자료 상에 두드러지게 확인되는 경계면(Fig. 2(a))의 발생원인분석으로 얕은 공기층이 있는 경우(Fig. 2(b)), 시공이 완벽하게 잘 이루어져 비접촉 구간이 없는 경우(Fig. 2(c)), 라이닝 배면 쪽에 공동이 크게 있어서 구조적 문제를 야기할 수 있는 경우(Fig. 2(d)) 등 다양한 경우가 존재할 수 있다. 그러나 이에 대한 정확한 분석기술의 부재로 강한 반사파가 존재하는 다른 매질의 경계면이 존재할 것이라는 정도의 분석만 가능한 실정이다.
따라서 본 연구에서는 1차적으로 현장에서 발생 가능한 조건의 모형체 제작과 이에 대한 GPR 시험 신호를 획득하여 라이닝 내부와 배면의 정확한 상태에 대응하는 GPR 신호 DB(Data Base)를 확보하고자 하였다. 하지만, GPR 신호 획득과 패턴 분석 기법 개발을 위해서는 보다 다양한 조건에 대한 GPR 신호가 필요함에도 불구하고 모든 조건에 대해 모형시험체를 제작하고 이에 대한 시험으로 DB를 확보하는 것은 현실적으로 불가능하다. 따라서 각종 노이즈 없이 보다 깨끗한 신호 패턴을 얻을 수 있는 수치해석을 통해 보다 다양한 조건에 대한 GPR 신호 DB를 확보하고 활용할 필요가 있다. 본 연구에서는 python 언어 기반의 오픈소스코드인 gprMax 소프트웨어를 이용하여 터널 라이닝 모형 시험체 조건에 대한 GPR 신호특성을 정량적으로 분석하고 평가할 수 있는 수치해석 기법을 제안하였다. 또한, 해석 결과의 예측 신뢰성을 검증하고자 도출된 GPR 신호 특성을 모형체 시험 데이터와 비교·검토하였다. 검증이 완료된 수치해석모델을 이용하여 터널 라이닝 두께, 방수막의 영향 등 다양한 구조물 상태 별 해석을 통해 조건 변화에 따른 신호 패턴 변화를 확인하고자 하였다.
2. 터널 라이닝 모형시험체 제작 및 GPR 시험
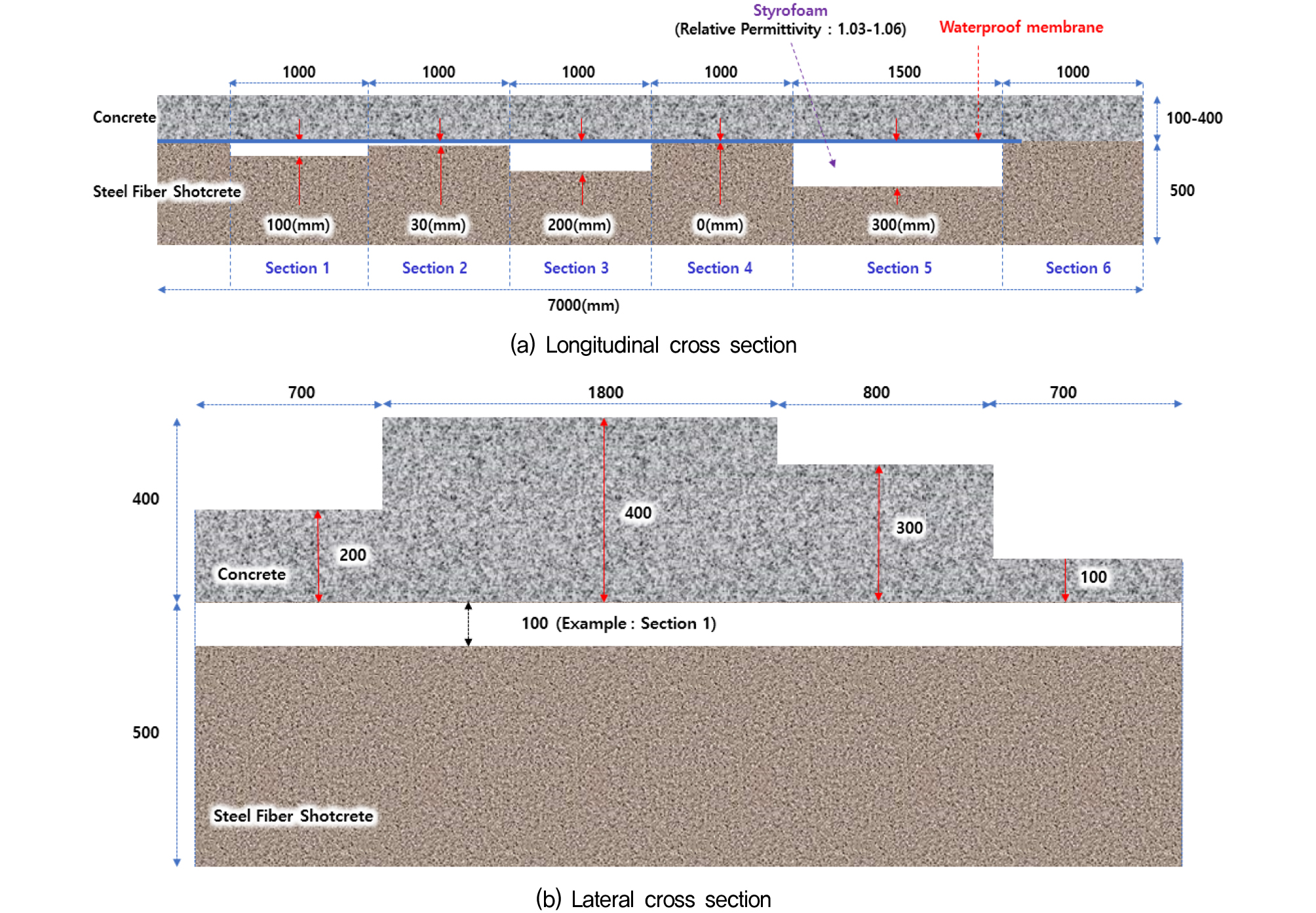
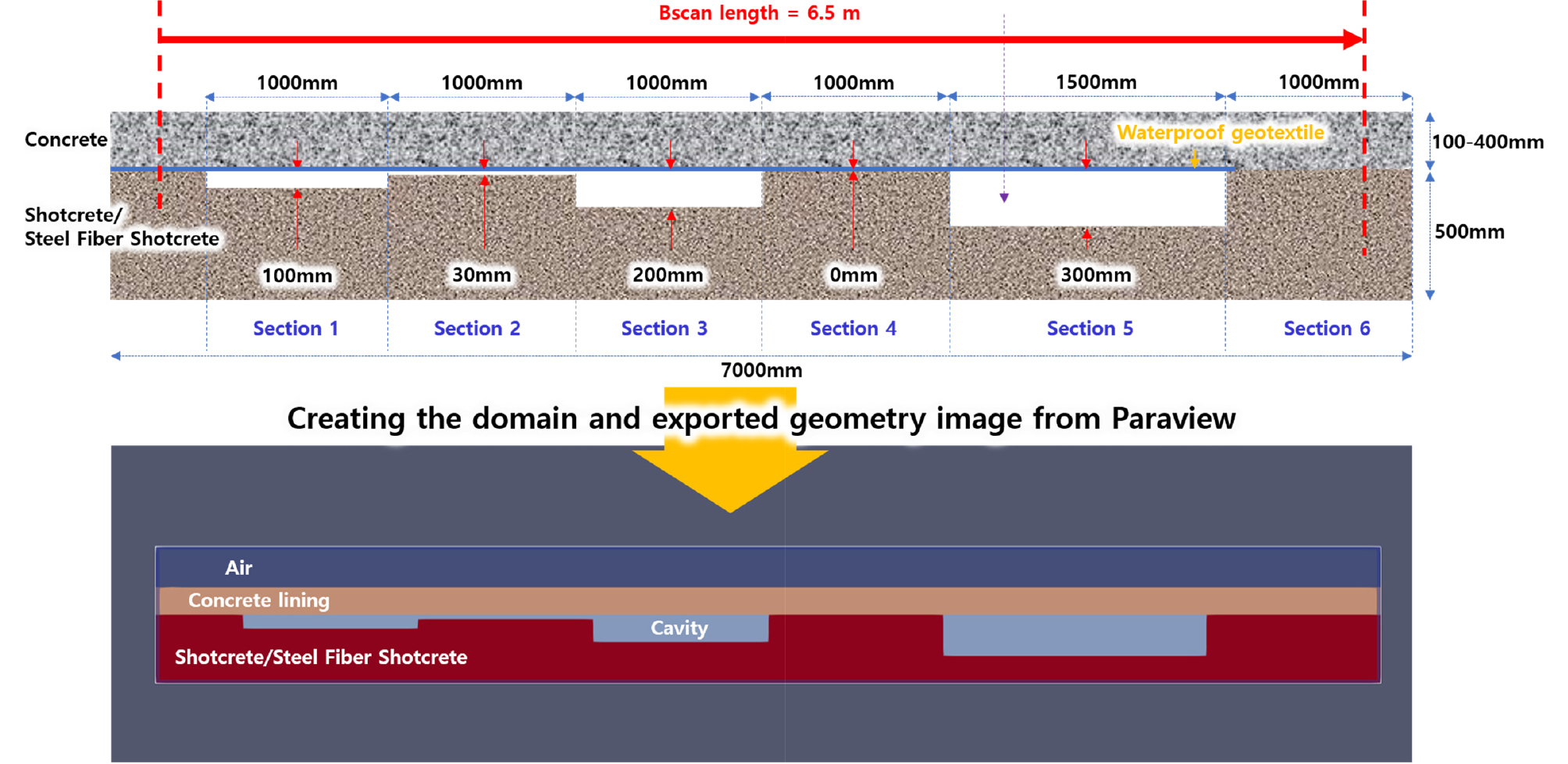
본 연구에서는 터널 라이닝의 두께, 내부의 공동 존재와 규모 등을 GPR 검측에 의해 평가하기 위한 분석 기법 개발에 필요한 데이터를 확보하기 위해 수치해석을 수행하고 검증하는 것을 목표로 하고 있다. 이를 위해 먼저 사용된 수치해석모델의 신뢰성 검증을 위해 실제 터널에서 존재할 수 있는 라이닝과 숏크리트 접촉면 조건을 공동 유무 및 공동 크기 등에 따라 6가지로 모사하여 모형시험체를 Fig. 3(a)와 같이 제작하였다. 각 Section 별 경계면 조건에 대한 상세 규격 정보는 Table 1에 제시되었다. 또한, 터널 라이닝의 두께에 의한 영향을 확인하기 위해 Fig. 3(b)와 같이 200mm, 400mm, 300mm, 100mm 조건으로 라이닝의 두께를 달리하여 시험 모형체를 제작하였다. 한편, 탐사에 사용한 GPR 장비는 미국 GSSI(Geophysical Survey Systems, Inc.) 사의 장비를 사용하였으며, 지면접촉식(Ground-coupled)으로 시험을 수행하였다. 또한 안테나는 고주파와 저주파 안테나의 시험 모형체 파형 변화에 따른 적용성 분석을 위하여 400MHz 및 1600MHz의 2가지 주파수 대역에서 시험을 수행하였다. 터널 라이닝 모형에 대한 GPR 시험은 종단면도의 좌측에서 우측방향으로 즉 Section 1에서 Section 6 방향으로 GPR 장비를 이용시켜가며 데이터를 취득하였다(Fig. 4).
Table 1.
Section description of test model
3. 수치모델링
3.1 구성방정식
본 연구는 터널 라이닝 및 배면에 존재하는 공동을 수치해석적으로 탐지하고자 오픈소스 프로그램인 gprMax(Giannopoulos, 2005)를 이용하여 GPR의 신호응답을 모사하였다. gprMax는 Maxwell 방정식을 지배방정식으로 사용하며, 편미분방정식의 해를 근사화하기 위해 공간과 시간의 연속성을 이산화하는 유한차분 시간영역(Finite-difference time-domain)법을 사용하여 근사해를 구한다(Yee, 1996).
여기서, E는 전기장 강도(V/m), B는 자속밀도(T), t는 시간(ns), H는 자기장 강도(A/m), D는 전속밀도(C/m2), JC는 안테나 요소에서의 전류 밀도(A/m2), JS는 저항 소자에 흐르는 전류 밀도(A/m2), qv는 체적전하밀도(C/m3)를 의미한다.
기본적으로 gprMax는 3차원 공간상의 전자기장 해를 구할 수 있도록 개발되었다. 하지만 본 연구에서는 해석의 효율화를 통한 매개변수연구의 용이성을 위해 2차원 TM(transverse magnetic) z-direction 모드를 이용한 해석을 수행하였다. 이 경우 Maxwell 방정식은 다음과 같이 3개의 상호 연계된 편미분방정식 형태로 표현될 수 있으며, 시간과 공간에 대해 이산화되어 Fig. 5에 표시된 각각의 FDTD 셀에 적용된다.
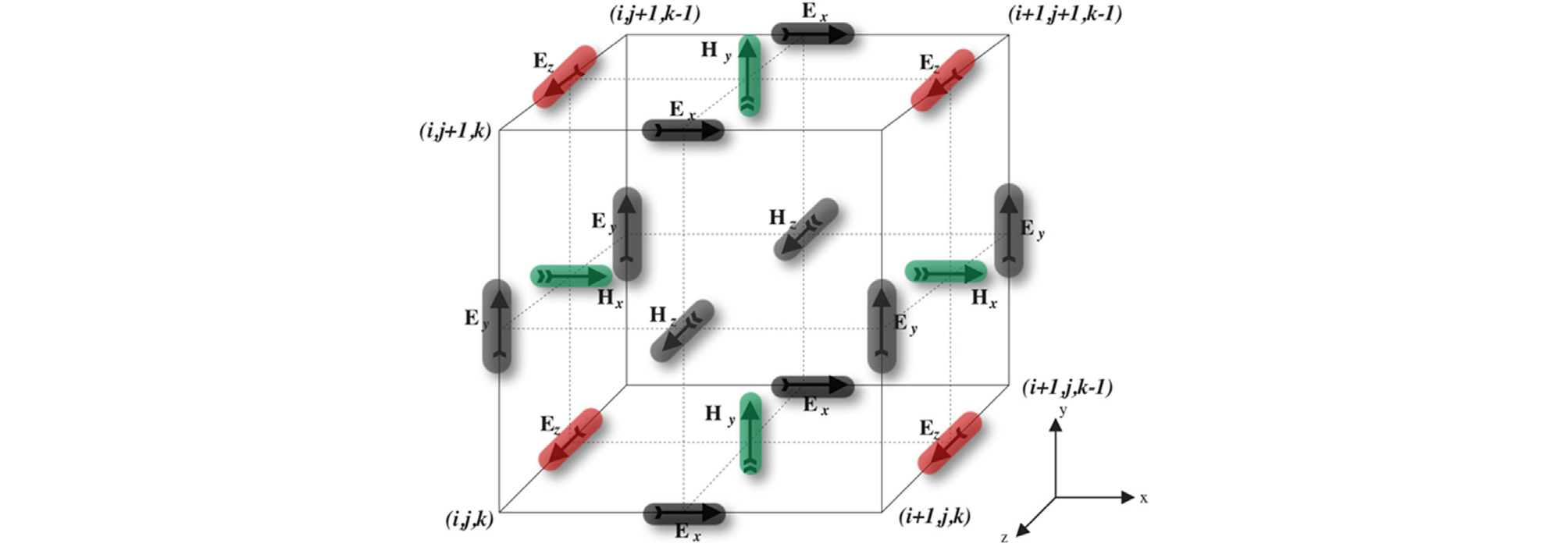
Fig. 5
Single FDTD Yee cell showing electric (red), magnetic (green), and zeroed out (grey) field components for 2D TMz mode (Yee, 1966)
여기서, ɛ는 유전율(farads/meter), μ는 투자율(henries/meter), σ는 전기전도도(Siemens/meter), σ*는 자기손실(Ohms/meter)를 의미한다.
3.2 재료 물성 및 GPR 안테나 제원
본 연구에서는 Fig. 6과 같이 모형체시험과 동일한 조건으로 해석 도메인을 구성하였다. 수치해석에 적용된 각 Type 별 재료 물성은 관련문헌(Cassidy, 2008)을 통해 확인된 값의 평균치를 사용하였고 이를 Table 2에 나타내었다. 또한, 시험에서 사용된 2가지 종류의 GPR 장비(400MHz, 1600MHz)에 대해 해석을 수행하였고, 각 안테나의 사양은 Table 3에 제시되었다. 파형의 종류는 해당 장비에서 일반적으로 사용되는 ‘Gaussian waveform’을 사용하였다. 수치해석에서 전자기파 소스와 관련된 중요한 입력 정보 중 하나는 바로 중심주파수(centre frequency, Hz)이다. 본 연구에서는 Taguchi method(Taguchi et al., 2005; Warren and Giannopoulos, 2011)를 통해 3가지 GPR 장비에 대한 중심주파수를 산정하여 해석모델에 적용하였다. 2차원 모델의 TMz 모드에서는 GPR 장비의 안테나는 3차원적인 구조를 모두 형상화하지 않고 송신부와 수신부를 각각 하나의 점(point)으로 간주하여 해석이 수행된다. 본 연구의 모형체 시험에서 사용된 장비는 지면접촉식(Ground-coupled)방식이기 때문에 해석 모델에서 안테나 위치는 지표면과 완전히 맞닿은 것으로 간주하였다. 또한, 송신부와 수신부 사이의 이격거리는 실제 거리를 감안하여 85mm로 설정하였다.
Table 2.
Material properties used in the numerical simulation model
| Type | Parameter | Value | Unit | Reference |
| Air/Cavity | Relative permittivity, ϵr | 1.045 | - | Cassidy, 2008 |
| Electric conductivity, σ | 0 | Siemens/meter | ||
| Relative permeability, μr | 1 | - | ||
| Magnetic loss, σ* | 0 | Ohms/meter | ||
| Shotcrete | Relative permittivity, ϵr | 12 | - | |
| Electric conductivity, σ | 0.005 | Siemens/meter | ||
| Relative permeability, μr | 1 | - | ||
| Magnetic loss, σ∗ | 0 | Ohms/meter | ||
| Concrete | Relative permittivity, ϵr | 7 | - | |
| Electric conductivity, σ | 0.005 | Siemens/meter | ||
| Relative permeability, μr | 1 | - | ||
| Magnetic loss, σ∗ | 0 | Ohms/meter | ||
| Waterproof membrane | Relative permittivity, ϵr | 3 | - | |
| Electric conductivity, σ | 0.001 | Siemens/meter | ||
| Relative permeability, μr | 1 | - | ||
| Magnetic loss, σ∗ | 0 | Ohms/meter |
Table 3.
Specification of GPR Antenna
| Type | GSSI 1.6 GHz | GSSI 400 MHz | Unit |
| Range | 12 | 50 | ns |
| High pass filter, f1 | 250 | 100 | MHz |
| Low pass filter, f2 | 3000 | 800 | MHz |
| Samples per scan | 512 | 512 | - |
| Scans per second | 100 | 120 | - |
한편, 해석모델에서 이산화된 요소(셀)의 크기인 Δx, Δy, Δz 및 미소시간 Δt의 크기를 적절하게 정의하는 것이 매우 중요하다. 요소의 크기 및 미소시간간격이 작을수록 실제 신호의 전파거동과 더 유사해지지만 해석을 수행하는 전산장비의 제한된 메모리 공간과 유한한 처리속도를 감안하기 위해서 적정 수준의 크기 및 간격을 정의하는 것이 요구된다. 해석에서 요구되는 요소(cell) 크기는 파장 길이(λ)의 1/10보다 작아야하며 파장길이 λ는 식 (3)을 통해 산정된다.
여기서, c는 빛의 속도 2.99×108m/s이며, f는 신호의 최대주파수(Hz), εr은 지반재료의 상대유전율을 의미한다.
4. 결과 및 분석
4.1 수치해석 결과 및 검증
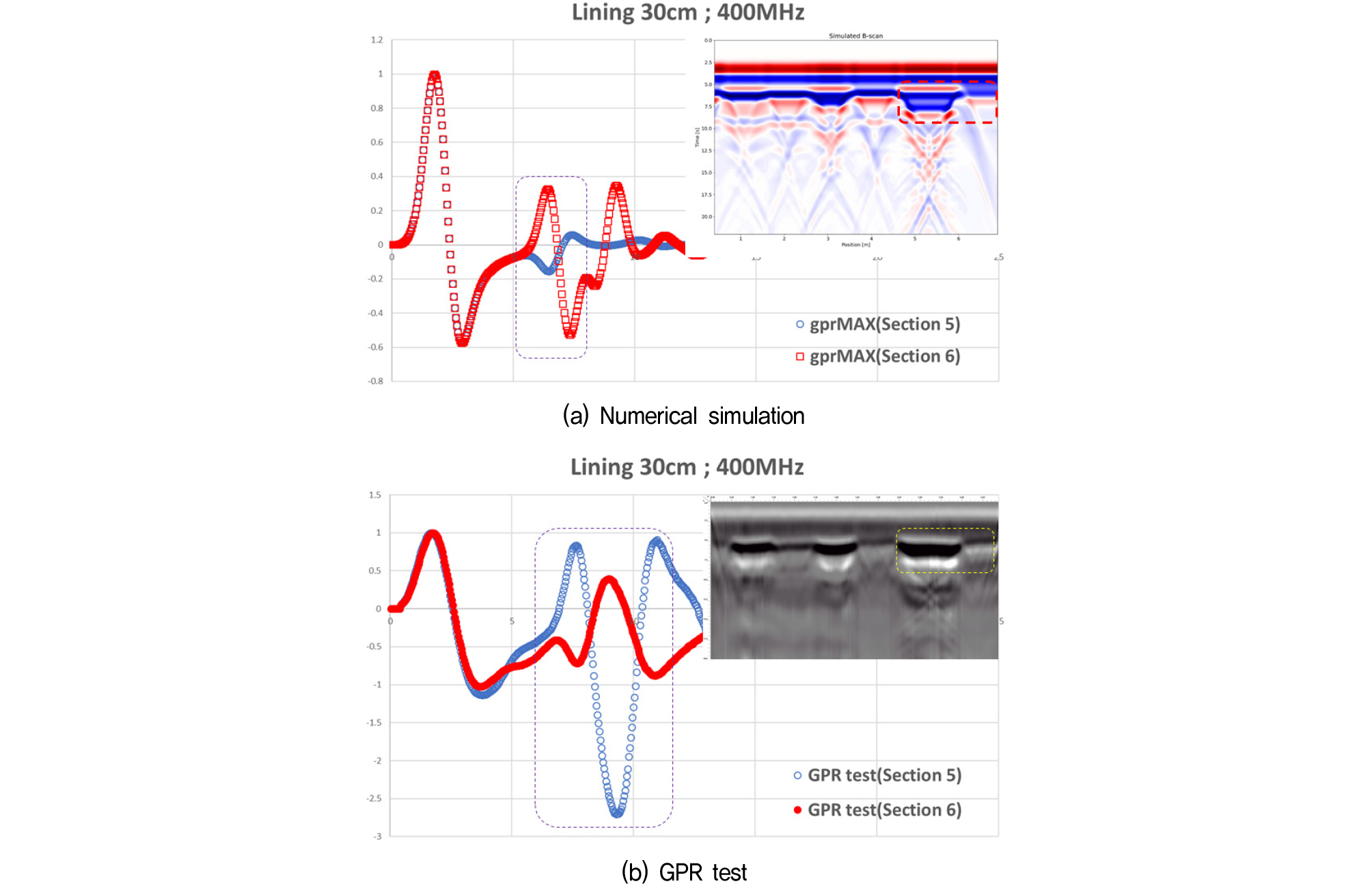
지반탐사레이더 분야에서 가장 많이 활용되는 분석 자료에는 A-scan과 B-scan이 있다. A-scan은 각 측선의 깊이방향의 전자기파 진폭을 1차원적으로 나타낸 자료, B-scan은 1차원 자료인 A-scan을 탐사방향(GPR 이동방향)으로 연속적으로 이어 붙인 2차원 이미지자료이다. 본 연구에서는 앞서 설명된 수치해석 기법을 적용하여 모형시험체를 대상으로 해석을 수행하여 각 단면별로 B-scan 이미지를 획득하였고, 이중 400MHz 해석 결과의 예시를 Fig. 7에 도시하였다. 해석결과에서 보이는 바와 같이 콘크리트 라이닝과 숏크리트층의 경계면, 콘크리트 라이닝과 공동의 경계면이 뚜렷하게 반사파로 나타난다는 것을 확인할 수 있었다. Fig. 8은 400MHz로 수행된 수치해석 결과와 시험결과를 비교한 결과이다. 결과에서 보이는 것과 같이 수치해석과 모형체 시험 결과의 반사파 패턴이 거의 유사한 것을 확인할 수 있었다. 전체적으로 공동이 있는 Section 1, 2, 3, 5와 공동이 없이 콘크리트 라이닝이 직접 숏크리트와 접하는 Section 4, 6에 비해 반사파의 강도가 더 큰 것을 경계면 신호에서 볼 수 있다. 이처럼 공동부가 상대적으로 더 큰 반사파 강도를 보이는 것은 각 재료의 유전율의 차이로 설명할 수 있을 것이다. 즉, 유전율의 차이가 클수록 반사파의 강도(R)가 크게 나타난다. 본 모형시험체의 경우 약 7-10 사이의 유전율을 갖는 콘크리트에서 유전율이 1에 가까운 공동의 공기층으로 전파될 때, 그 차이가 콘크리트와 숏크리트의 유전율 차이에 비해 상대적으로 더 크기 때문에 GPR 신호의 반사파 강도가 크게 나타나는 것으로 분석된다(Fig. 9 참조) 또한, A-scan 결과를 보여주는 Fig. 10에서도 확인할 수 있듯이 콘크리트를 통해서 공동 또는 숏크리트층을 투과할 때 반사파의 위상이 변하는 현상을 해석 및 시험결과에서 볼 수 있었다.
상기 기술된 결과들을 종합하면, 실제 GPR 시험의 경우 모형시험체 내부의 터널 라이닝, 숏크리트 등 매질의 유전율에 따라 투과 및 반사파의 강도와 패턴이 달라질 수 있었다. 또한, 현장에서 불가피하게 형성되는 다양한 노이즈 또는 경계면 등에서 만들어지는 반사파로 인해 중첩된 신호가 만들어지기도 하였다. 이에 반해 해석의 경우 노이즈가 없는 완벽하게 깨끗한 재료들로 이루어진 모형에 대한 해석으로 결과를 얻게 되기 때문에 현장 신호와 완벽하게 일치된 결과를 얻는 것은 불가능하였다. 즉, GPR 시험에서 얻어지는 결과는 현장 조건에 따라 다양하고 일관되지 않은 노이즈가 포함되어 분석하고자 하는 매질 조건이나 경계면 조건의 패턴 확인을 방해할 수 있기에 다양한 구조물 조건 변화에 따른 신호의 특징과 패턴을 분석하기에는 제안된 해석 모델이 더 유용하게 활용될 수 있을 것이라 판단된다. 본 연구의 해석결과와 GPR 시험에서 취득한 신호와 비교 검증한 결과 터널 라이닝과 내부 공동 등 매질 변화에 대한 전자기파 신호를 합리적으로 해석하는 것으로 판단할 수 있었다. 향후 다양한 터널 라이닝과 배면 상태의 조건별로 수치해석 결과를 GPR 분석 기법 개발에 적용이 가능할 것으로 기대된다.
4.2 라이닝 두께, 방수막의 영향
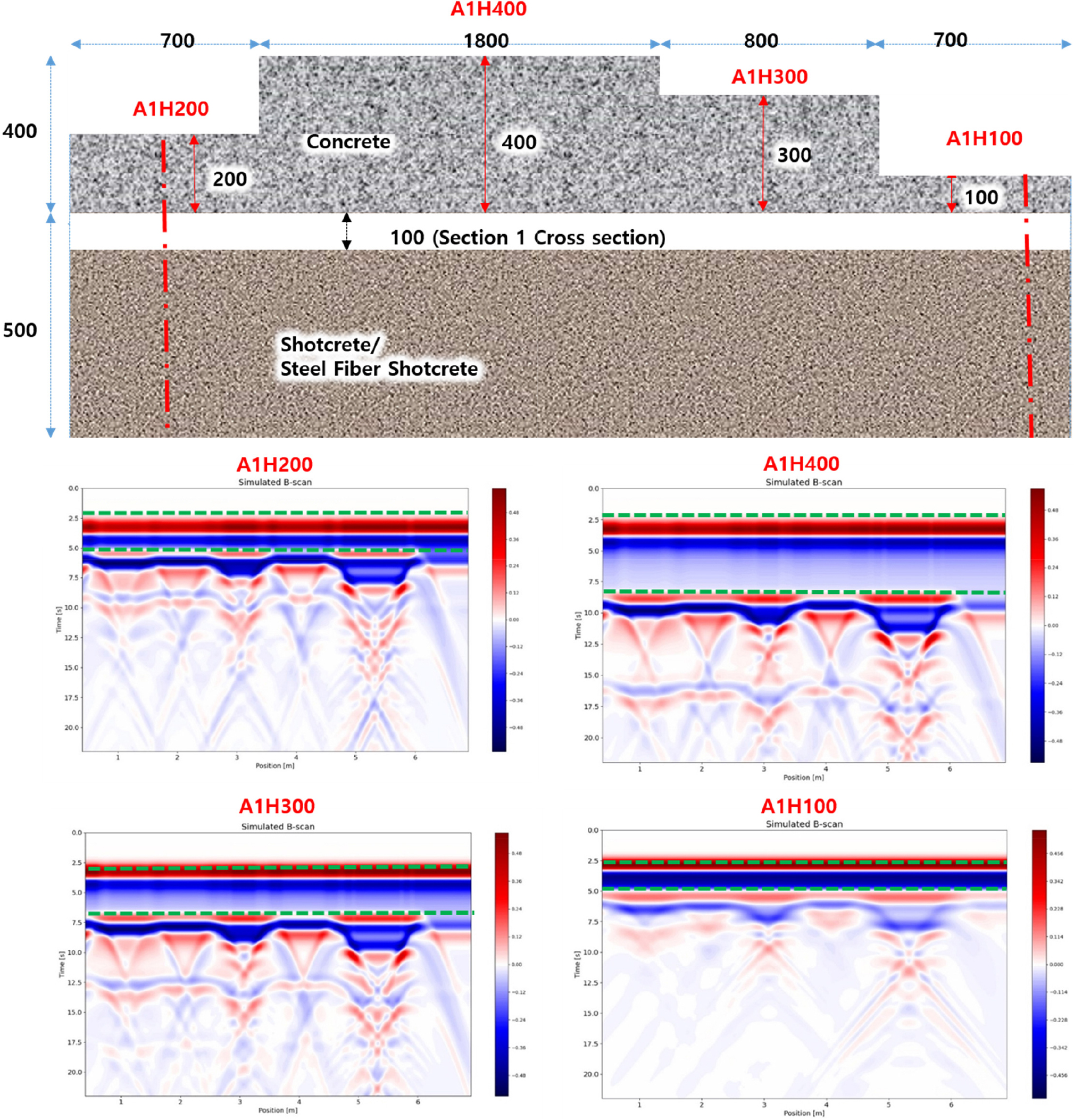
GPR 시험을 통한 터널 라이닝 두께 및 내부 상태를 추정하는 방법은 대체로 B-scan 이미지 상에 나타나는 반사파 신호의 상대적인 강도 차이를 식별해서 분석하는 것이 일반적이다. 본 연구에서는 터널 라이닝 끝단에 누수 방지 목적으로 설치되는 방수막(waterproof membrane)이 B-scan 상의 신호 패턴에 어느 정도 영향을 줄 것이라고 판단하였고 어떤 조건에서 얼마만큼의 영향을 미치는지를 수치모델에서 도출된 다양한 B-scan을 이용하여 확인하고자 하였다.
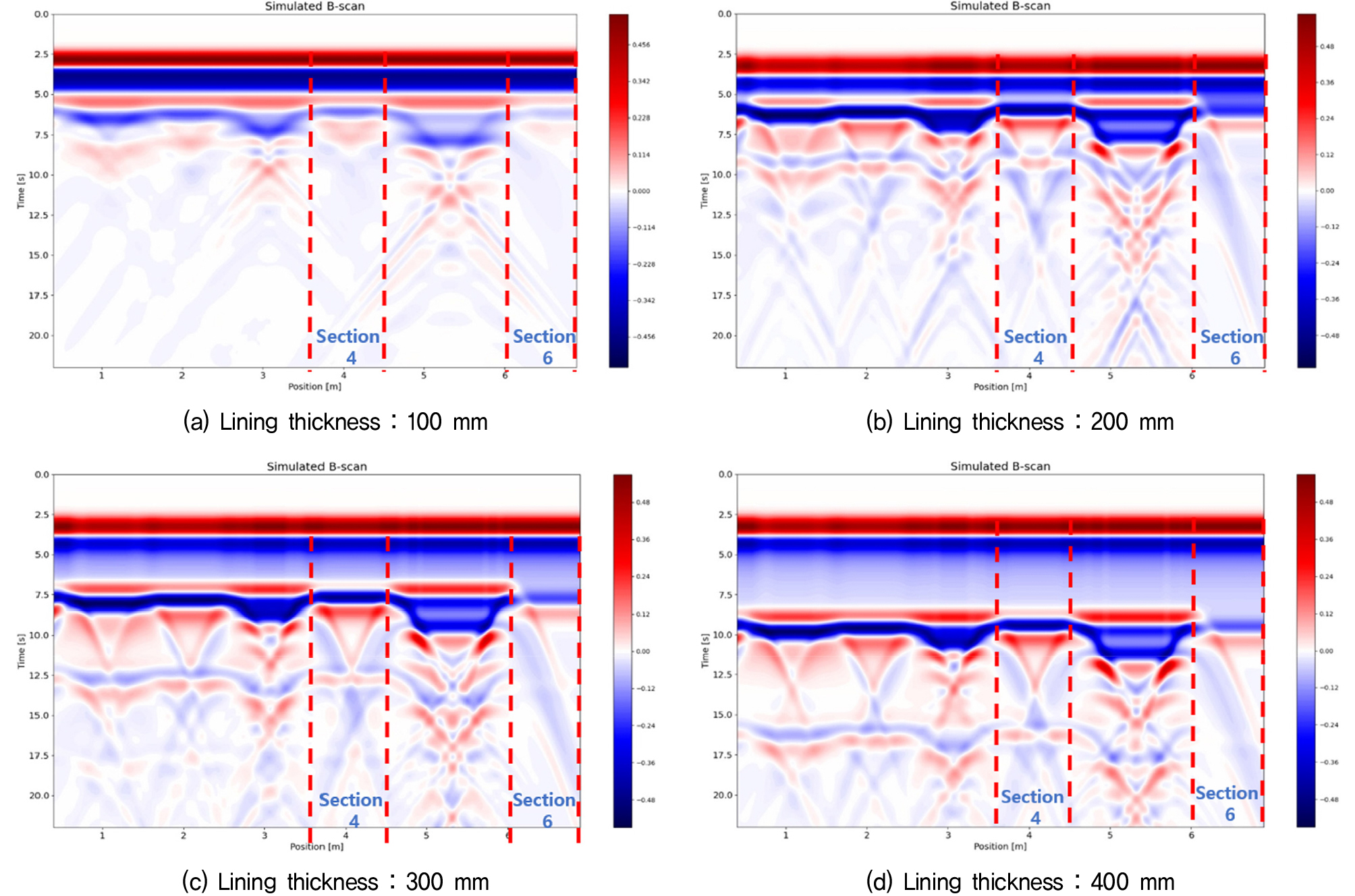
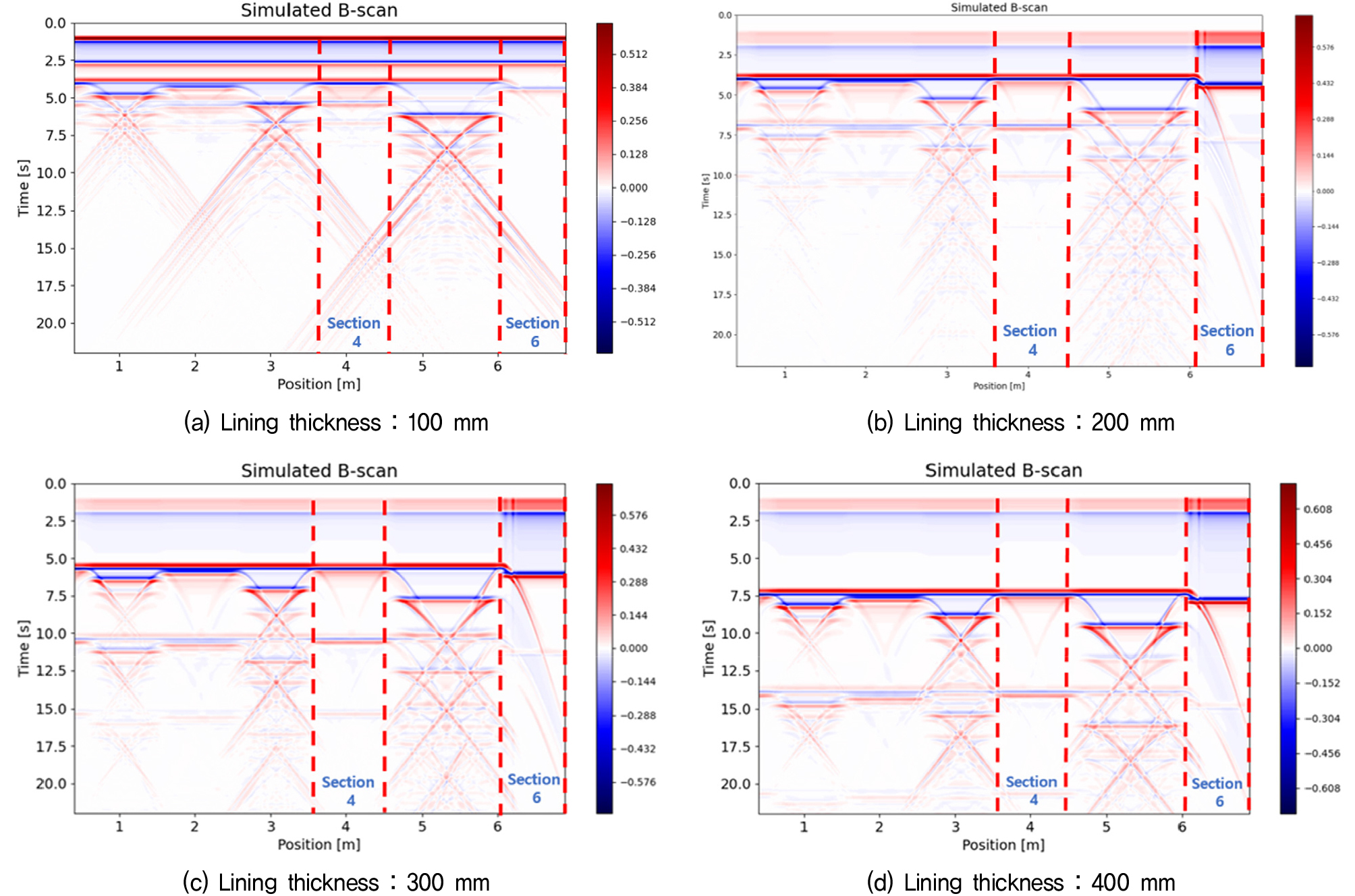
Fig. 11과 Fig. 12는 터널 라이닝 두께, 방수막 유무, 주파수 조건에 따라 변화되는 신호 패턴을 확인할 수 있는 B-scan 이미지 결과이다. 특히 B-scan상의 Section 4와 Section 6은 라이닝과 숏크리트 사이에 공동이 존재하지 않는 영역으로서 순수하게 방수막의 영향만을 확인할 수 있는 비교자료로서 의미를 지닌다. 해석결과에 따르면 터널 라이닝과 숏크리트 사이에 존재하는 방수막으로 인하여 수신부로 돌아오는 반사파의 강도가 훨씬 약해짐을 알 수 있다. 즉 안테나에서 송출된 전자기파는 방수막을 통과하면서 일부 에너지가 산란되며, 이로 인해 수신부로 돌아오는 반사파의 크기가 상대적으로 감소하였다. 이러한 감쇄현상은 라이닝이 충분히 두꺼운 조건일 때 더 확연하게 나타났다. 또한, 방수막이 존재하지 않는 경계면(Section 6)에서는 방수막 두께만큼 라이닝이 추가적으로 존재하기 때문에 라이닝에 의한 반사파의 파장이 1초정도 길어졌고 경계면에서의 반사파 신호의 위상 또한 Section 1-5 대비 반전되어 나타나는 결과를 확인하였다. 방수막의 영향은 안테나 주파수 대역대가 400MHz일 때보다 1600MHz인 조건일 때 더 크게 나타났다. 이는 파장 길이가 짧은 고주파일수록 두께가 30mm밖에 되지 않는 방수막 객체의 형상(Geometry) 및 물성(Material) 차이를 시간적, 공간적으로 구분하기에 유리한 측면이 있었을 것으로 분석된다. 따라서 제안된 수치해석모델은 터널 라이닝 내의 공동 유무 여부, 이상체의 경계면까지의 터널 라이닝의 두께 평가 뿐 아니라 방수막의 유무(이탈여부)를 확인하기 위한 GPR 신호의 분석에 있어서도 적극적으로 활용될 수 있을 것으로 기대된다.
5. 결 론
본 연구에서는 gprMax 소프트웨어를 이용하여 터널 라이닝 모형 시험체 조건에 대한 GPR 신호특성을 정량적으로 분석하고 평가할 수 있는 수치해석을 수행하였고, 터널 라이닝 모형체 시험 결과와 비교하여 해석모델의 예측 신뢰성을 검증하였다. 검증된 수치해석모델을 이용하여 터널 라이닝의 두께, 내부의 공동 존재와 규모 등을 GPR 검측에 의해 평가하기 위한 분석 기법 개발에 필요한 데이터를 확보할 수 있었고, 이를 통해 도출된 결론은 다음과 같다.
(1) 모형체 시험 및 수치해석의 GPR 신호자료를 분석한 결과, 콘크리트 라이닝과 숏크리트층의 경계면, 콘크리트 라이닝과 공동의 경계면이 뚜렷한 반사파로 B-scan 상에 표시되었고, 수치해석과 모형체 시험 결과의 반사파 패턴이 거의 유사한 것을 확인할 수 있었다. 또한, 공동이 있는 Section이 공동이 없는 Section에 비해 상대적으로 반사파 강도가 더 크게 나타났다. 이는 숏크리트의 공기의 유전율 차이로 인한 반사파 강도가 달리 나타났기 때문인 것으로 사료된다.
(2) 본 연구에서 적용된 GPR 해석모델은 터널 라이닝 및 내부 공동 등 매질 변화에 대한 전자기파 신호변화를 합리적으로 모사하였다. 향후 다양한 터널 라이닝과 배면 상태를 확인하는 GPR 분석 기법 개발에 있어서 수치해석모델의 적용성이 높을 것으로 기대된다.
(3) 본 연구에서 수행된 다양한 수치해석연구를 통해 터널 라이닝과 숏크리트 사이의 방수막의 유무를 콘크리트 라이닝에서 숏크리트(혹은 공동)으로 투과하고 반사되는 반사파의 위상변화 여부로 판단이 가능하다는 사실을 확인할 수 있었다. 추후 해석모델에 다양한 변수를 적용해서 반사파 중첩에 따른 파장의 특성 변화, 주파수대역별 산란특성 등을 평가할 수 있을 것으로 사료되며, 구조물 상태 별 분석 기법 개발에도 제안된 해석모델이 효과적으로 활용할 수 있을 것으로 기대된다.