1. 서 론

지진 시 사면에는 정적하중에 추가적인 하중이 가중된다. 사면에서는 이러한 지진하중을 고려하는 방법과 해석방법에 따라 일반적으로 유사정적해석법과 뉴마크 방법(강성블록해석법) 그리고 동적해석방법으로 구분한다(MOLIT, 2020). 유사정적해석법은 1906년 샌프란시스코 대지진 이후 1916년 일본의 Sano 교수에 의해 제안된 것으로 알려져 있으며(Towata, 2008), 한계평형해석법(Limit Equilibrium Analysis Method)에 근거하여 사면에 대한 지진하중의 영향을 개략적으로 평가하는 방법이다(Pushpa et al., 2017). 유사정적해석법은 해석에 활용되는 지진계수의 선정의 불확실성과 등가정적하중 치환의 적절성에 대한 단점들에도 불구하고 지진 시 사면안정에 대한 판단기준이 안전계수로 제시되어 있다는 점과 과거에 축적된 풍부한 경험자료 그리고 동적해석방법에 비해 쉽게 안전계수의 산출이 가능하다는 점 때문에 현재까지 실무적으로 가장 널리 사용되고 있다(Jibson, 2011; Melo and Sharma, 2004; California Geological Survey, 2008).

Newmark(1965)는 지진시 사면의 영구변위를 평가하기 위하여 진동하는 경사면 위에 놓인 강체블록의 움직임을 분석하였다. 이때 강체블록의 움직임은 지진으로 인한 사면의 활동면의 변위와 유사하다는 결론을 바탕으로 사면의 활동면을 강체블럭으로 가정한 간편한 변위 경험식을 제안하였다.

일반적으로 Newmark(1965)의 영구변위식 뿐만 아니라 사면을 강체 또는 연성 블록으로 모사하며 항복 가속도를 초과하는 가속도 펄스를 이중적분하여 영구 변위를 계산하는 모든 기법을 Newmark 활동블록방법 또는 줄여서 Newmark 방법으로도 부른다. 국내 비탈면 내진설계기준 KDS 11 90 00: 2016에서 허용되는 연구변위는 비탈면높이의 1%이다. Newmark 방법은 건조 사질토 지반의 변위를 예측하는데 적합하지만, 토체에서의 지진동 감쇠효과와 지반의 강도변화를 고려하지 못하는 것으로 알려져 있다(Cho et al., 2003).

지진 시 사면의 동적거동을 평가하는 데 있어서 지반의 비선형성을 고려하는 응답이력해석은 여러 장점을 가지고 있지만 소요 연산시간이 길기에 국내에서 일반적으로 수행되고 있지 않다(Lee et al., 2015; Lee et al., 2020). 또한 비탈면 내진설계기준 KDS 11 90 00: 2016에는 응답이력해석법으로 사면의 안정성을 평가하는 기준이 제시되지 않았다. 참고로 응답이력해석법으로 계산된 사면에서의 영구변위는 Newmark의 영구변위와는 개념적으로 다르므로 사용될 수 없다. 응답이력해석으로부터 동적 안전계수를 산출할 수 있다면 유사정적해석법의 단점을 극복하는 동시에 내진설계기준에 기초한 평가까지 가능해지므로 활용도 높아진다.

본 연구에서는 유사정적해석의 가장 큰 문제점인 단일 지진계수을 적용하지 않으며, 지진동 시간이력에 따라 변화되는 동적 안전계수 시간이력 산출이 가능한 응답이력해석 절차를 개발하였다. 이 절차에서는 비선형 지반거동을 고려할 수 있으며 사전에 정의된 복수의 활동면에 작용하는 응력의 적분으로부터 시간단계별 사면의 최소 안전계수 시간이력을 계산한다. 이 방법은 단일 사면 사례에 적용하여 동적 안전계수와 유사정적해석으로 계산된 안전계수를 비교하였다.

2. 수치해석 방법

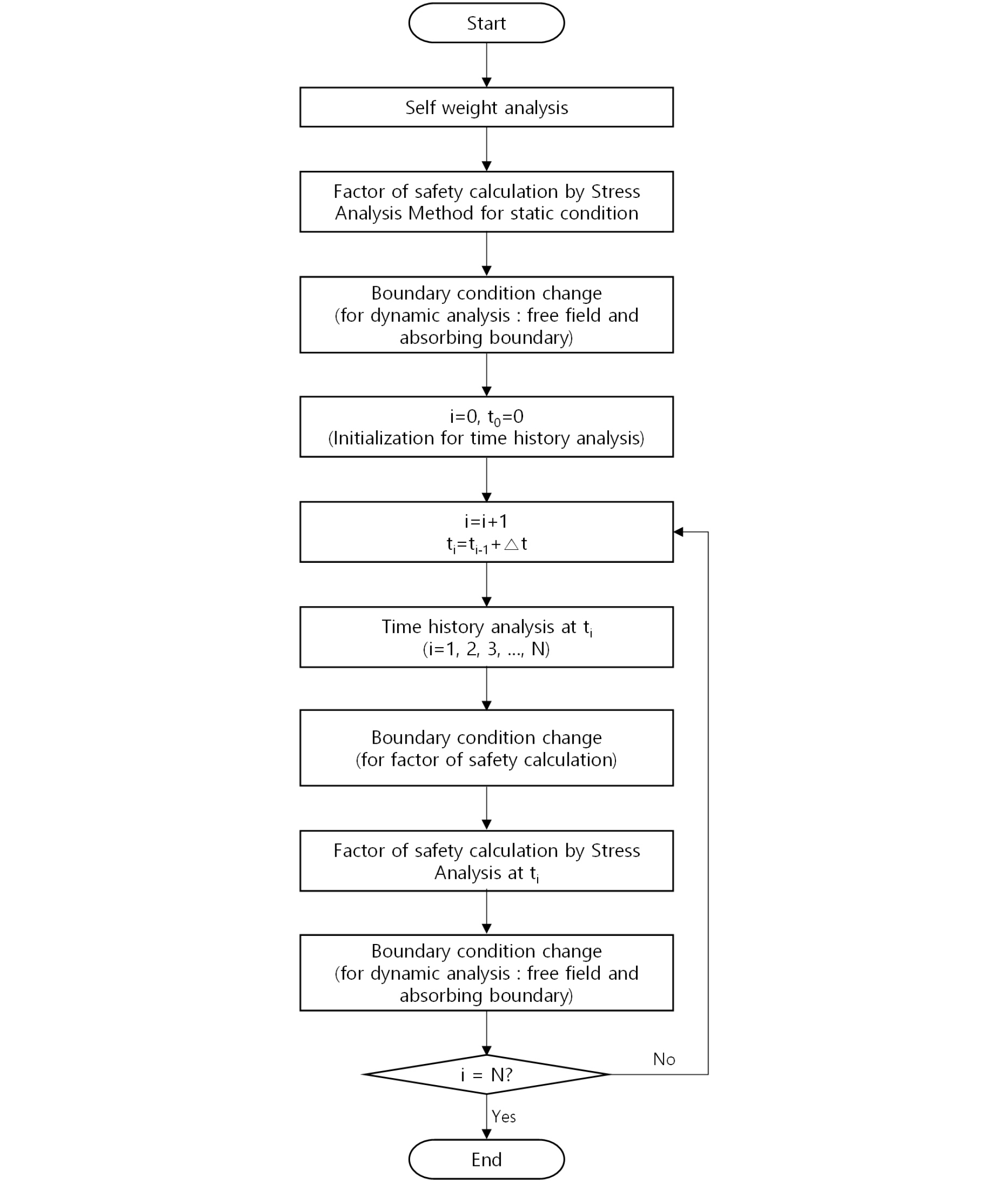
비선형 응답이력해석으로부터 사면의 동적 안전계수를 계산하는 절차는 Fig. 1에 정리하였다. 사면의 동적 안전계수 계산은 먼저 초기응력상태를 재현한 후, 정적 상태에서 발생한 가능한 활동면을 산정한다. 활동면은 임의로 정해진 정적 안전율의 범위에 포함되는 모든 면을 선정한다. 활동면 중에서 안전계수가 가장 작게 계산되는 면을 임계면으로 결정하며 이에 대한 안전계수도 산정한다.

Fig. 1

Dynamic factor of safety calculation procedure in slope

이후 응답이력해석을 수행하면서 매 시간단계에서 계산된 활동면에 대한 동적 안전계수를 계산한다. 미리 정의된 활동면에 대한 전단응력과 전단강도의 비를 활용하여 사면의 안전계수를 계산하는 방법은 아래와 같다.

여기서, FS : 사면의 안전계수

τ_f : 전단강도

τ : 전단응력

L : 활동면 길이

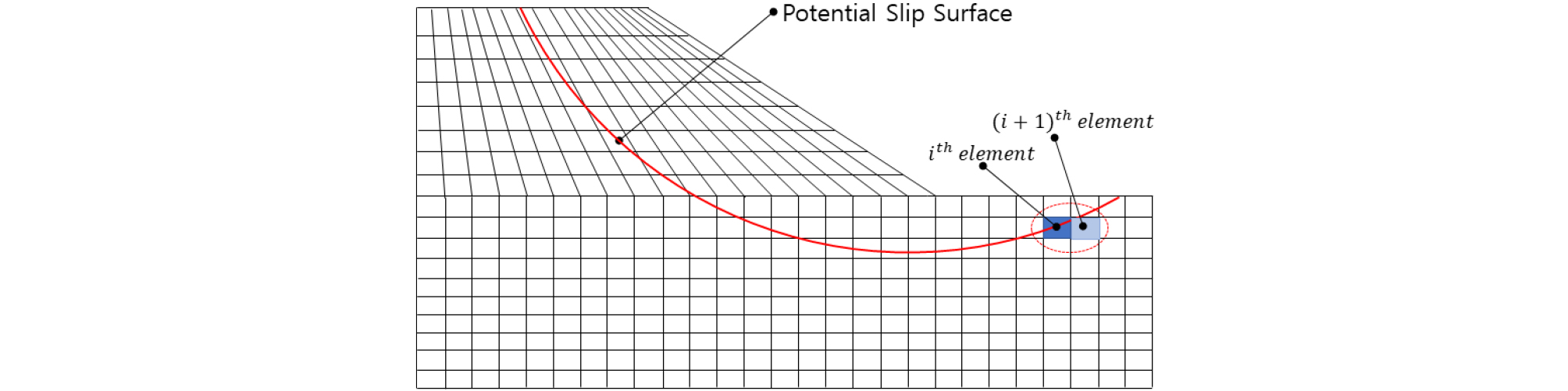
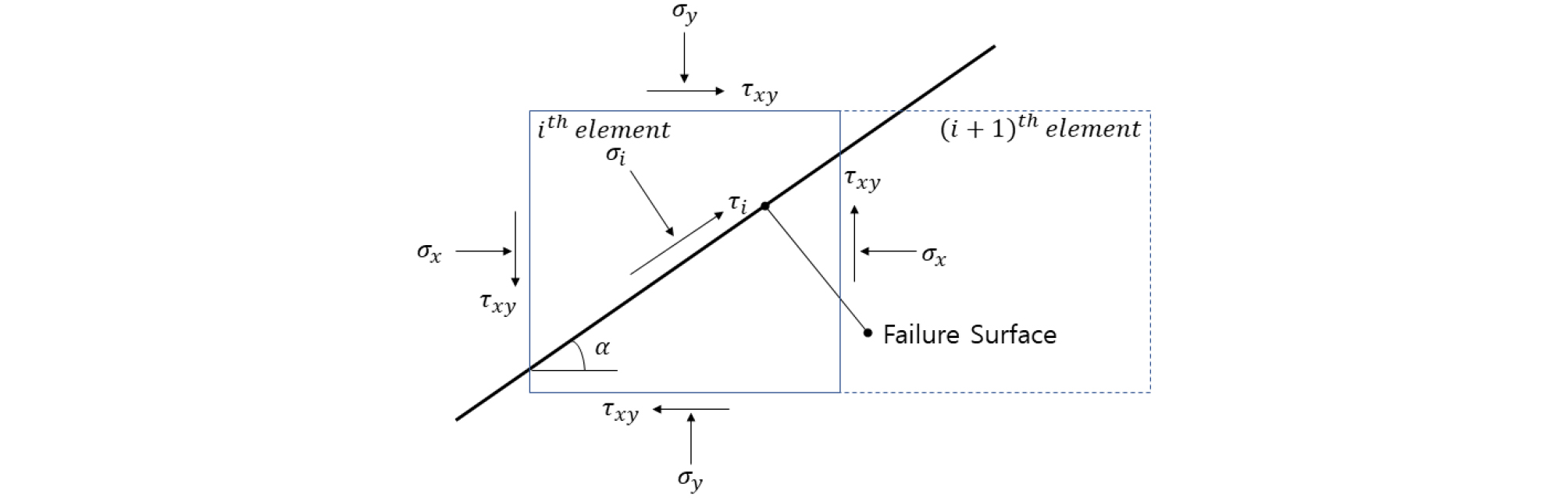
즉, 미리 정의된 가상의 활동면에 대하여 Mohr-Coulomb 파괴규준에 따른 전단강도의 합과 수치해석 계산결과로 얻어지는 전단응력의 합의 비로 정의된다. Fig. 2와 Fig. 3에 나타낸 바와 같이 활동면이 포함된 i번째 요소에서의 전단응력과 전단강도는 식 (2)∼(4)로부터 계산할 수 있고, 각 요소에서의 응력을 계산한 다음 가상의 활동면 전체에 대한 전단응력과 전단강도의 합으로부터 사면의 안전계수를 계산한다.

Fig. 2

Potential slip surface

Fig. 3

Normal and shear stress at i^th element

여기서, c : 점착력

ϕ : 내부마찰각

α : 수평면과 활동면이 이루는 각도

σ_i : σ_x, σ_y, τ_xy로부터 산정된 가상의 활동면에 수직방향으로 작용하는 법선응력(normal stress)

τ_i : σ_x, σ_y, τ_xy로부터 산정된 가상의 활동면에 수평방향으로 작용하는 전단응력(shear stress)

응답이력해석법으로부터 시간에 따라 변이하는 안전계수를 산정할 수도 있으며, 발생 가능한 포괄적인 활동면에 대하여 계수를 산정하므로 지진파와 사면의 동적 응답 특성을 고려한 가장 취약한 활동면을 산정할 수 있으므로 유사정적해석법과 응답이력해석법의 장점을 모두 가지고 있다고 볼 수 있다. 위의 두 가지 기법이 융합된 기법은 범용 유한요소해석 프로그램인 DIANA FEA(2021)에 구축하였다. 나아가 DIANA FEA에는 비선형 지반 거동을 모사하기 위한 새로운 모델을 개발하여 탑재하였다.

3. 수치해석

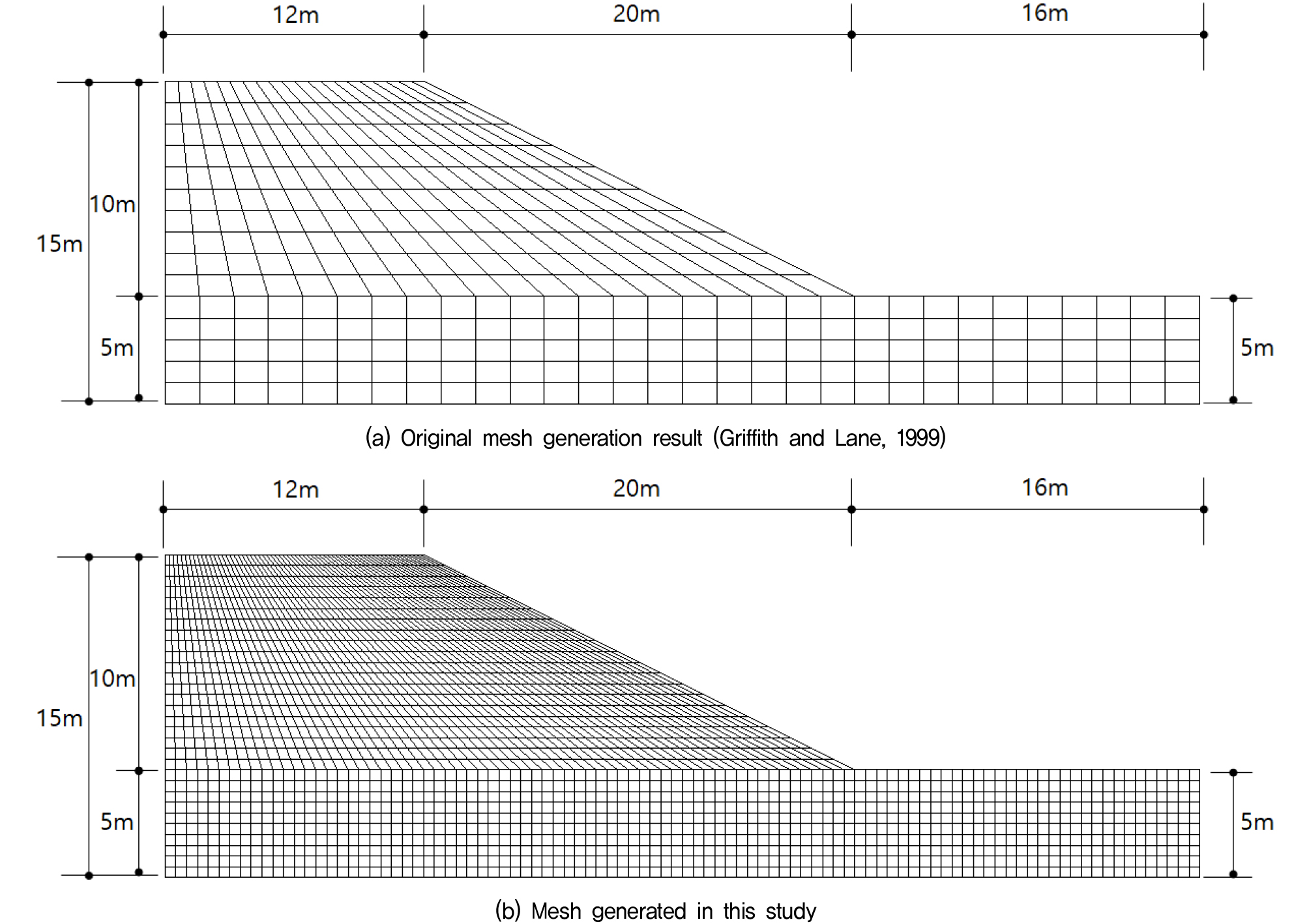
본 연구에서는 Griffith and Lane(1999)이 사용한 사면 모델을 대상으로 적용하였다(Fig. 4). 동적해석에 적용된 하부 경계조건은 반사파 영향을 최소화할 수 있는 점성댐퍼(viscous damper)를 적용하였으며, 측면 경계조건은 점성댐퍼가 연결된 측면경계에 자유장 조건을 적용하였다. 동적해석을 수행하기에 앞서 지진파의 주파수 성분의 필터링이 발생하지 않도록 Kuhlemeyer and Lysmer(1973)가 제안한 요소의 최대 크기보다 작게 요소를 재구성하였으며 이는 식 (5)와 같다.

Fig. 4

Numerical slope model

여기서, △l : 요소 길이

V_s : 매질의 전단파 속도

f : 전달가능한 주파수

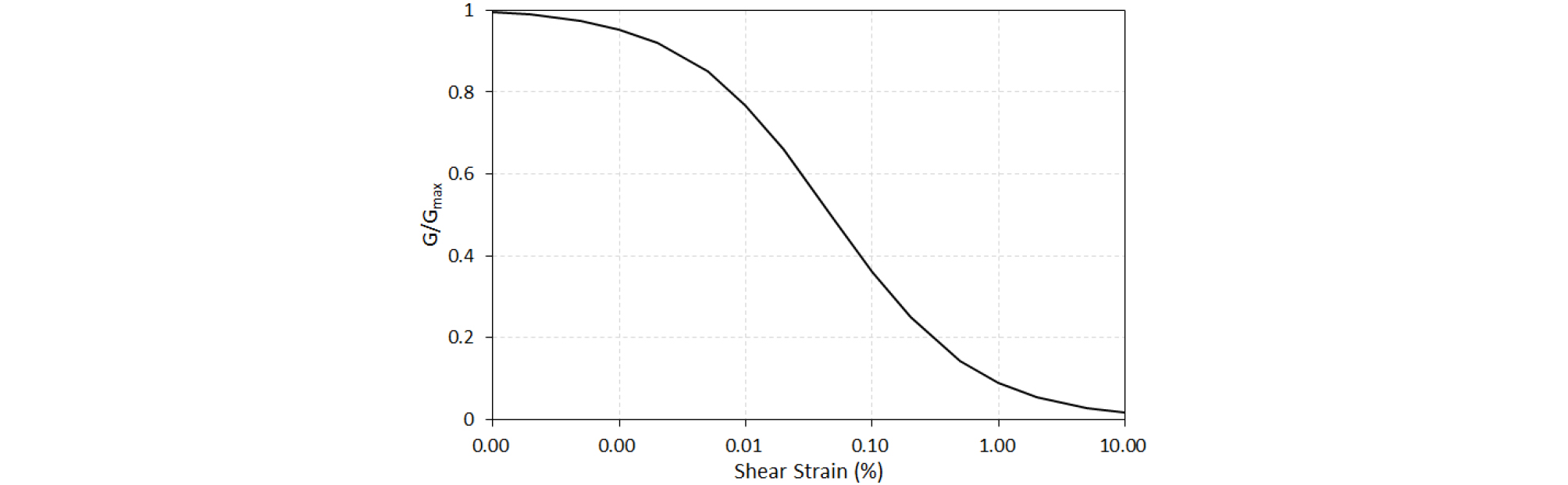
적용된 요소의 최대높이는 0.5m이다. 해석에 이용된 입력물성치는 Table 1에 정리하였다. 정적해석에서 사용한 단위중량과 점착력 및 내부마찰각을 동일하게 사용하였으며, 동적해석을 위한 전단탄성계수 감소곡선은 사면 중앙부에서의 구속압 조건을 고려한 Darendeli(2001)의 모래 곡선을 사용하였다(Fig. 5).

Fig. 5의 전단탄성계수 감소곡선으로부터 초기 재하곡선(backbone curve)을 직접 계산하며 재하 및 제하곡선은 확장된 Masing 법칙에 의거하여 계산하였다. 사용된 비선형 모델은 소성 모델이 아니며 흐름규칙에 의거하여 소성 변형을 계산하지 않는다. 기존 연구에서 비선형 곡선과 Mohr-Coulomb 모델을 결합하여 응력이 전단강도에 도달하는 경우에 적용된 팽창각에 따라 non-associated 또는 associated 흐름규칙을 이용하여 소성 변형을 계산한 사례가 있다(Lee et al., 2015). 하지만 국내 지진환경 수준에서는 소성상태에 도달해서 발생하는 변형이 크지 않을 것으로 예상된다. 무엇보다 전단강도에 도달한 이후에 발생하는 소성변형이 연구변위에는 일정 영향을 미칠 수도 있지만 안전율에 미치는 영향은 제한적일 것으로 예측되므로 이를 고려하지 않았다.

Fig. 5

Shear modulus reduction curve used in this study

동적해석을 수행하기 위한 입력지진동으로 인공시간이력을 활용하였으며(Fig. 6), 최대지반가속도(peak ground acceleration, PGA)는 0.2g이다. 예상 활동면은 Fig. 7에 도시한 바와 같이 한계평형해석법에서 일반적으로 사용하는 기법인 다수의 원호 중심과 지반 내 접선(tangential line)을 이용하여 생성하는 방식으로 산정하였다. 대상 사면에서는 123개의 활동면들을 미리 정의하였으며 이는 Fig. 7에 도시하였다.

Fig. 6

Characteristics of input ground motion

Fig. 7

Predefined potential slip surfaces

4. 수치해석 결과분석

4.1 정적 사면안정해석 결과

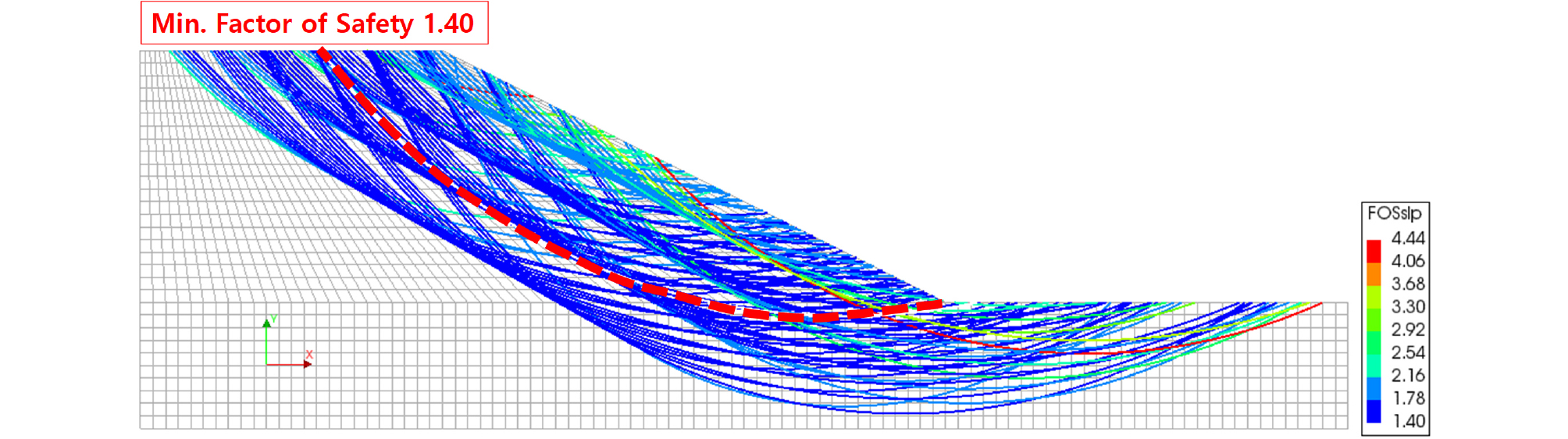
사면의 정적 안전계수를 계산하기 위해 미리 정의된 123 개의 활동면을 대상으로 계산한 결과 최소 안전계수는 Fig. 8에 나타낸 바와 같이 1.4였다. 이 결과는 동일한 사면에 대한 기존의 연구결과(Griffith and Lane, 1999) 및 한계평형해석결과로부터 계산된 최소 안전계수와 일치한다. 위의 비교로부터 본 연구에서 구축한 수치해석 툴이 정확하다는 것을 확인하였다.

Fig. 8

Min. factor of safety of slope for the static condition in this study

4.2 동적 사면안정해석결과

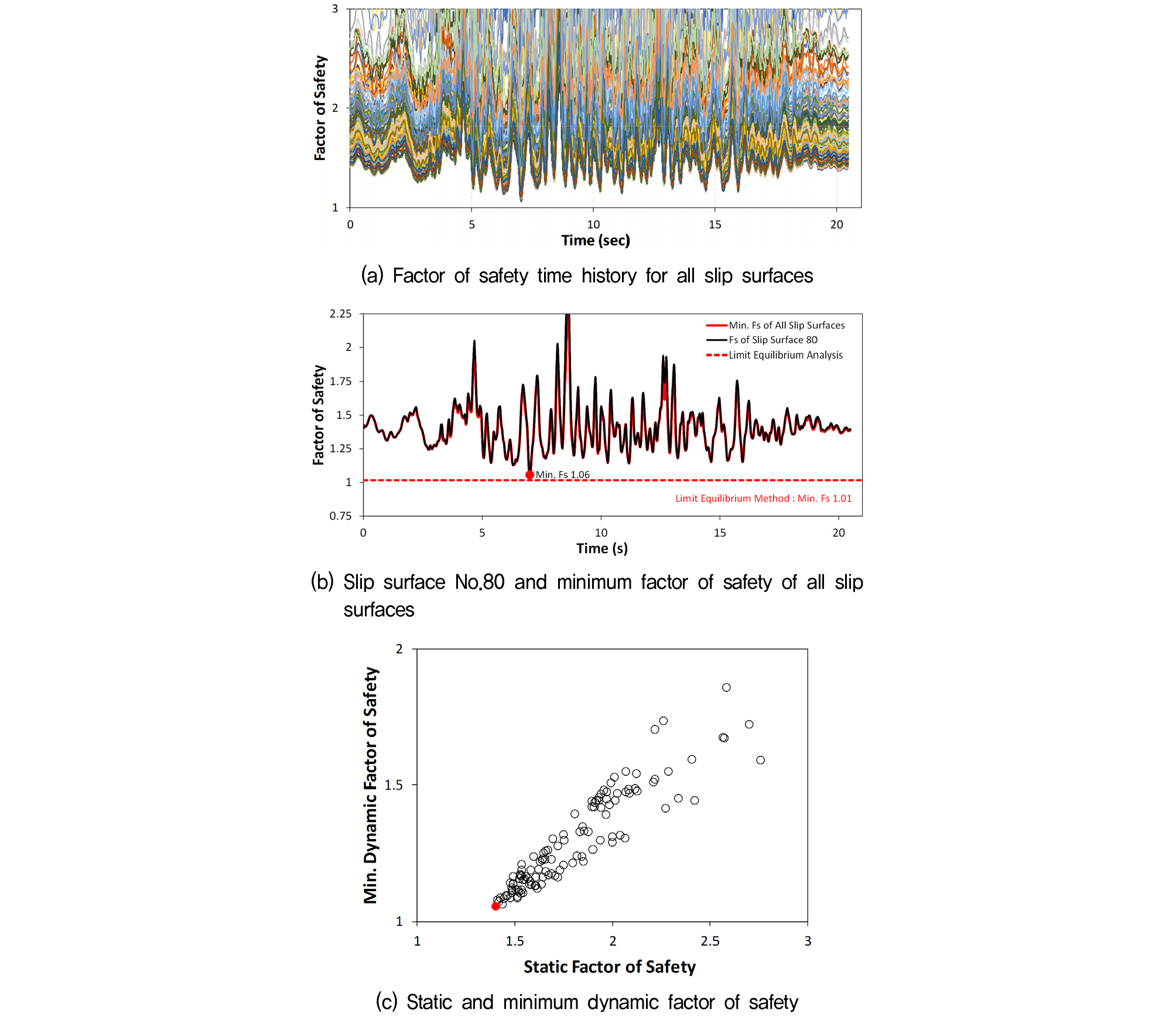
본 연구에서 유사정적 해석법을 이용한 사면의 수평방향 지진계수 계산은 Hynes-Griffin and Franklin(1984)의 제안식에 단주기 증폭계수를 곱하여 적용하였으며, 계산된 대상사면의 최소 동적 사면 안전계수는 1.01로 평가되었다. Fig. 9(a)는 비선형 응답이력해석과 미리 정의된 123개의 활동면 전체에 대한 안전계수 시간이력 계산결과를 나타낸 그림으로 입력지진동이 지반하부에 가력됨에 따라 사면의 안전계수는 계속 변화하며, 활동 토체의 관성력 작용방향에 따라 안전계수가 정적해석결과와 비교하여 커지거나 작아진다. 이에 반해 유사정적 해석법의 경우 지진하중을 지진계수를 통해 등가의 수평하중으로 치환하여 적용하기 때문에 지진 시간이력에 대한 사면의 안전계수는 시간에 대한 안전계수가 단일한 값으로 표현된다. 또한 입력지진동의 최대 지반가속도 발생시점과 사면의 동적 최소 안전계수 발현 시점은 직접적인 상관관계는 없는 것으로 평가되었다. 이는 일반적으로 최대 지반가속도 발현시점에서의 지진파 성분과 지반의 고유진동수는 서로 무관하기 때문인 것이라고 추정된다.

응답이력해석으로 123개 활동면 전체에 대하여 계산된 최소 동적 사면 안전계수는 1.06으로 평가되었으며, 유사정적 해석결과와의 1.01과 비교하여 약간 더 크게 나타났다(Fig. 9(b)).

Fig. 9

Factor of safety of slope

또한 123개 전체 활동면들에 대하여 각각의 지진 시각에서 계산된 안전계수 값들 중 최소값만 선택하여 안전계수 시간이력으로 도시한 결과와 정적 사면안정해석에서 안전계수가 가장 낮게 평가된 80번 활동면에 대한 안전계수 시간이력을 비교하였을 때 일부 구간에서 80번 활동면의 안전계수가 약간 더 크지만, 전체적으로는 매우 유사한 경향성을 보인다. 이는 정적상태에서 안전계수가 낮은 활동면이 동적해석에서도 낮은 안전계수를 가진다는 것을 의미한다.

특히, Fig. 9에 나타낸 바와 같이 전체 활동면들에 대한 정적 안전계수와 최소 동적 안전계수의 관계는 정적상태에서 안전계수가 낮은 활동면들은 한 점으로 수렴되는 경향성을 보이며, 반대로 정적 안전계수가 높은 활동면들은 최소 동적 안전계수의 변동성이 크게 증가함을 알 수 있다. 이러한 관계로부터 해석의 효율성을 증대시키기 위하여 정적 사면안정해석을 수행한 다음, 안전계수가 낮은 활동면들을 대상으로 동적해석을 실시하고 안전계수 시간이력을 구하는 경우 해석의 효율성이 크게 높아질 수 있음을 암시하고 있다.

본 연구에서 유사정적해석에 적용된 수평방향 지진계수는 0.15이다. Fig. 10(a)에 도시한 바와 같이 활동면 전체에 대한 수평방향 지진계수 값의 범위는 -0.206∼0.204이며, 동적해석으로부터 계산한 수평방향 지진계수 최대값이 유사정적해석법에서 가정한 값에 비해 더 크게 나타났다. 활동면 전체에 대한 수평방향 지진계수 평균값을 파란색 굵은 실선으로 표시하였고, 지진계수의 작용방향과 관성력의 작용방향은 동일하기 때문에 지진계수가 사면 외측으로 향하는 경우 사면의 안전계수는 감소하며, 반대인 경우 사면의 안전계수는 증가하는 경향성을 보였으며, 특히 수평방향 지진계수가 최대가 되는 시점인 7.015초에서 사면의 안전계수는 최소값을 나타냈다. 또한 본 연구에서는 수평방향 지진동만을 입력하였으나, Fig. 10(b)와 같이 연직방향 지반 운동이 발생하였으며, 이는 사면의 기하학적 형상과 비대칭성으로 인한 지진파의 반사와 굴절 등의 영향으로 내부 응력상태의 변화와 연직방향 작용력의 변화에 기인하는 것으로 판단된다. 수평방향 입력지진동에 의해 발생되는 연직방향 지진계수는 본 대상사면에서는 수평방향 지진계수에 비해 최대 및 최소값을 기준으로 최대 17% 이내였다. 그러나 그림에 도시한 바와 같이 연직방향 지진계수와 사면의 최소 동적 안전계수 발현시점과는 직접적인 상관관계는 없는 것으로 나타났다. 123개의 활동면 토체 내부의 평균 가속도를 계산하여 Fig. 10(c)에 나타내었다. 여기서 평균 가속도는 활동면 상부 요소들의 가속도 평균을 나타낸다. 평균 계산 시 요소 크기에 대한 보정을 적용하였다. 전체 활동면 대상 각 활동면 토체 내에서 발생하는 평균 가속도 최대값은 약 0.212 g 이며, 80번 활동면 내부에 작용하는 최대 가속도 값은 0.124 g로 나타났다. 특히 80번 활동면 내부 토체의 평균 가속도 최대값 발생 시점과 최대 수평방향 지진계수 발생 시점 그리고 사면의 안전계수는 최소값 발생시점이 서로 일치하는 것으로 나타났다.

Fig. 10

Seismic coefficients and average horizontal acceleration of the slip body

5. 결 론

유사정적해석법은 실무적 관점에서 널리 이용되는 방법이다. 그러나 유사정적해석 시 이용되는 지진계수가 가지는 여러 가지 문제점들과 한계평형해석기법의 한계로 인해 지진 시 사면 동적거동을 설명하기에는 부적합하다. 반면에 비선형 응답이력해석을 포함한 동적해석은 지진 시 지반의 응력-변형관계를 가장 잘 설명할 수 있다는 장점에도 불구하고 각종 설계요건상의 기준이 되는 안전계수를 구하기 어렵다는 단점을 가지고 있어 본 연구에서는 유사정적해석과 동적해석의 장점을 모두 가지는 동적해석 방법을 제시하였다. 본 연구에서 도출된 결론은 다음과 같다.

(1) 비선형 응답이력해석으로부터 지진 시 사면의 안전계수 시간이력을 계산하였으며, 지진동에 의해 유발되는 관성력에 의해 사면의 안전계수는 시간에 따라 변화함을 확인하였다. 또한 최대지반가속도가 0.2g인 인공지진시간이력을 사용한 사례연구 결과에서 동적해석 결과로부터 계산된 사면의 동적 최소 안전계수는 유사정적 해석결과에 비해 약간 더 크게 평가되었다. 단, 이는 단일 사례연구의 결과이며 추후 다양한 사면과 지반운동에 대한 응답을 평가하여 동적 및 유사정적 안전계수와의 차이를 규명해야 할 필요가 있다고 판단된다.

(2) 정적 상태에서 안전계수가 낮은 활동면들이 동적 상태에서도 낮은 안전율을 보이는 것으로 평가되었다. 반대로 정적 상태에서 안전계수가 높은 활동면들은 동적 상태에서의 안전계수 변동성이 크게 증가하였다. 따라서 동적해석의 단점인 해석 소요시간의 단축을 위하여 정적 상태에서의 안전계수를 구한 다음 안전계수가 낮은 몇몇 활동면 대상으로 해석을 수행하는 경우 해석 효율성이 크게 증가할 수 있다.

(3) 사면의 동적 안전계수 시간이력과 마찬가지로 사면의 수평방향 지진계수와 활동 토체 내 평균 가속도는 시간에 따라 변화하며, 각각의 최대값 발현 시점에서 사면의 최소 동적 안전계수가 최소가 된다.

(4) 입력지진동으로 수평방향의 지진동만 입력하더라도 연직방향의 지반 운동이 발생하였으며, 이는 사면의 기하학적 형상과 비대칭성으로 인한 지진파의 반사와 굴절 등의 영향으로 내부 응력상태의 변화와 연직방향 작용력의 변화에 기인하는 것으로 판단된다.