1. 서 론

도시의 기반시설 중 상당 부분을 지하화하는 작업이 계속되고 있으며, 이 중 국내 지하공동구는 1969년 여의도 개발 시 건설한 것을 시작으로 신도시 개발 또는 택지개발 계획과 함께 꾸준히 건설되어왔다. 전력, 통신, 상수, 난방, 중수 등의 공급망을 구성하는 지하공동구는 도시기능을 유지하기 위한 핵심 기간망이며, 재난 및 재해로 서비스의 정지 및 일시적 중단이 발생하는 경우 대규모 사회경제적 손실을 가져온다. 사회기반시설인 공동구의 손상은 다수의 불편과 사회경제적 손실을 초래할 수 있으므로 관리 필요성이 증대되고 있다.

그간 지하공동구는 대부분 지진 발생 시 지상 구조물에 비해 상대적으로 경미한 피해만이 보고되었다(Wang, 1993). 지하공동구는 터널과 같이 지중에 완전히 매립 또는 굴착되어 시공된 구조물로 지상 구조물과 같이 증폭된 관성력에 의한 응답보다는 지반운동의 발생 시에 대해 주변의 토사나 암반과 함께 거동하는 경향이 있다. 또한, 일반적으로 지반운동의 진폭은 지표로부터의 깊이에 따라 감소하며 이러한 지중구조물의 지진피해가 적다고 알려져 있다(Power et al., 1998). 하지만, 지진에 의한 지중구조물의 다양한 피해 사례가 있었으며, 이 중 심각한 지중구조물의 손상은 단층운동(faulting)에 의한 지반변위와 관련되어 있다(O’Rourke et al., 2001; Owen and Scholl, 1981; Rowe, 1992; Ueng et al., 2001; Yu et al., 2016). 지반파열을 동반하지 않은 진동에 의한 지중구조물의 피해는 상대적으로 경미한 경우가 대부분이지만, 효고현 남부 지진 시 발생한 다이카이 지하철역 붕괴와 같이(EQE International, 1995; Iida et al., 1996; Nakamura et al., 1996) 중대한 손상의 가능성을 배제할 수는 없다. 특히 심도가 깊이 굴착되는 터널에 비해 얕은 토사지반에 개착식으로 설치되는 지하공동구의 경우에는 구조물 외벽에 횡토압 증가를 유발하는 일시적인 지반 횡변위에 특히 취약하다. 이러한 점에도 불구하고 공동구에 내진설계가 적용되기 시작한 것은 최근의 일이며, 대부분의 기존 공동구는 이러한 지진에 대한 고려 없이 설계 및 시공되었고 현재 많은 수가 적절한 내진평가 수행 없이 사용 중이다.

최근 이러한 문제점에 대한 인식이 높아져 공동구를 포함한 지중구조물의 내진평가가 점차 확대되고 있으며, 공동구 내진설계 관련 기준 및 평가방법이 개정 또는 신설되었다(MOLIT, 2021; KISTEC, 2020). 국내 지중구조물의 내진평가 시 가장 널리 사용하는 응답변위법 중 코사인법은 지반층에 대한 가정을 과도하게 단순화하여 지반응답해석에 비하여 지반변위를 과다 산정하는 경향이 있다. 단, 지반응답해석은 입력지진파 선정 및 적용에 있어서 국내의 지반환경에 부합한다고(hazard-consistent) 보기에 어려운 점이 있으며 실무자에 따라 다른 결과를 도출한다는 단점이 존재한다. 결과적으로 내진평가 수행 시 응답변위법의 결과가 충분히 신뢰성이 있는지 확인하기가 어렵지만, 대안이 될 수 있는 적정한 검토방법 또는 공학실무에 효율적이고 합리적으로 적용할 수 있는 방법이 부족한 것이 현실이다.

본 연구에서는 지하공동구의 위험분석 및 피해 예측에 있어서 기존의 방법에 비해 합리적이며 국내 지진환경을 반영한 지반변위 산정 방법을 제시한다. 이 방법은 지중구조물의 평가에 있어서 기존 평가법에 비해 국내의 지진환경에 부합할 뿐만 아니라 이를 확장하면 국내 지반분류에 따른 예상 지반변위의 범위를 도출하여 기존 응답변위법의 결과에 대한 검토 도구로 사용할 수 있다.

2. 응답변위법

지진 발생 시 터널 응답의 실제 관측과 원심모형시험기를 이용한 실험 결과 등을 통한 이해를 바탕으로 오늘날 지중구조물의 지진해석에 많은 발전이 있었다. 하지만, 지반운동의 특성과 지진파의 입사각, 전달과정, 지중구조물 주변의 지반의 특성과 지진 응답, 심도에 따른 지반과 구조물의 상대적 강성, 지반-구조물 상호작용 등 여러 가지 요인에 의해 지하공동구의 지진 거동을 정확하게 예측하는 것은 매우 어렵다.

지중구조물의 지진하중에 대한 거동 평가에 사용되는 방법은 입력 지진하중의 수단으로서의 지반변위 산정 단계와 지중구조물의 응답으로서의 역학적 거동 단계로 구분할 수 있다. 전자는 보통 응답변위법으로 대표되며, 이 과정에서 지중구조물 설치 깊이에서의 지반변위를 적정하게 산정하는 것이 지중구조물 해석의 핵심이다.

응답변위법은 지반운동에 발생하는 지반변위를 의사정적하중(pseudo-static load)으로 변환하여 입력 지진하중으로 사용하는 방법이다. 지중구조물은 지상 구조물의 경우와 달리 지반운동의 관성력에 의해 발생하는 상부구조의 증폭된 횡변위보다는 주변을 둘러싼 매질(지하공동구의 경우 일반적으로 토사층)에 의해 구속되어 있기 때문에, 공동구 구조물에 작용하는 직접적인 지진하중을 산정하는 방법보다는 지반변위를 기반으로 등가의 의사정적하중을 구조물에 적용하여 그 부재력 또는 부재응력을 평가하는 것이 널리 사용되어왔다.

2.1 단순화 가정법

응답변위법 중 지표면 또는 지중구조물이 위치한 대상 지반층의 변위 산정에 사용되는 단일 또는 이중코사인법으로 알려진 방법은 지반을 단일 또는 두 층으로 가정하여 지반의 변형 모드를 매우 단순화한 가정에 기초하고 있으며, 본 연구에서는 ‘지반층 단순화 가정법(또는 단순화 가정법)’으로 명칭한다.

실제 지중구조물의 해석에 있어서 국내 실무에서 주류를 이루는 응답변위법의 변위산정 시 흔히 사용하는 코사인법은 모두 이러한 지반층 단순화 가정을 기반으로 하고 있다. 즉, 전단파(SH-wave)에 의한 특성이 지배적인 지반운동에 대해서 대상 부지의 고유주기를 산정할 수 있다는 가정을 전제로 하여, 지반(토사층)의 고유주기에 따른 응답변위를 지반운동 또는 설계스펙트럼 값을 사용하여 산정하는 것이다. 이 방법은 단단한 암반층(half-space) 위에 균질한 단일층 토사로 구성된 지반층에서 심도에 따른 지반변형의 근사치를 특정 삼각함수 곡선으로 도식화할 수 있다는 전제를 기반으로 하고 있다(St. John and Zahrah, 1987). 단순화 가정법과 조합하여 사용하는 해석해는 지중 파이프망의 내진설계에 사용하기 위해 개발한 자유장의 지반변형률 관계식(Newmark, 1968)을 기반으로 St. John과 Zahrah가 제안한 것을 시초로 하고 있다.

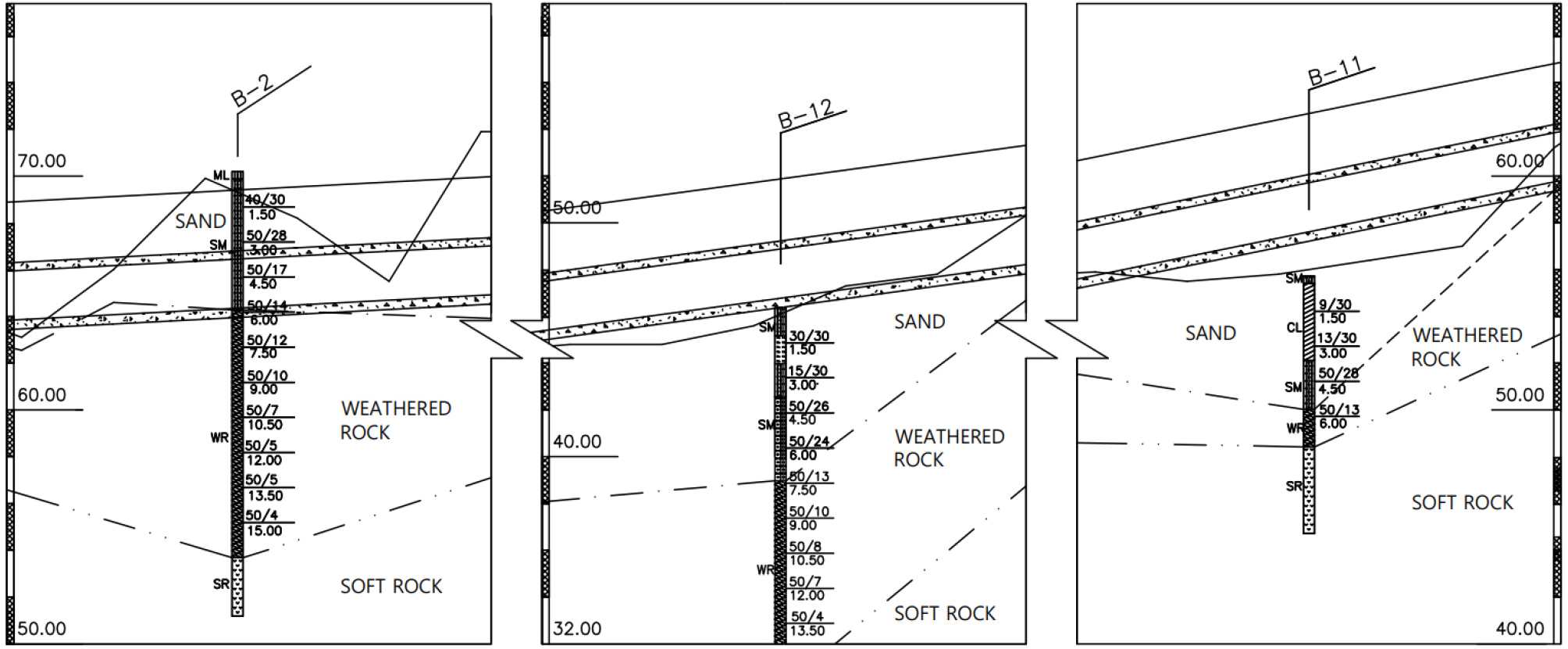
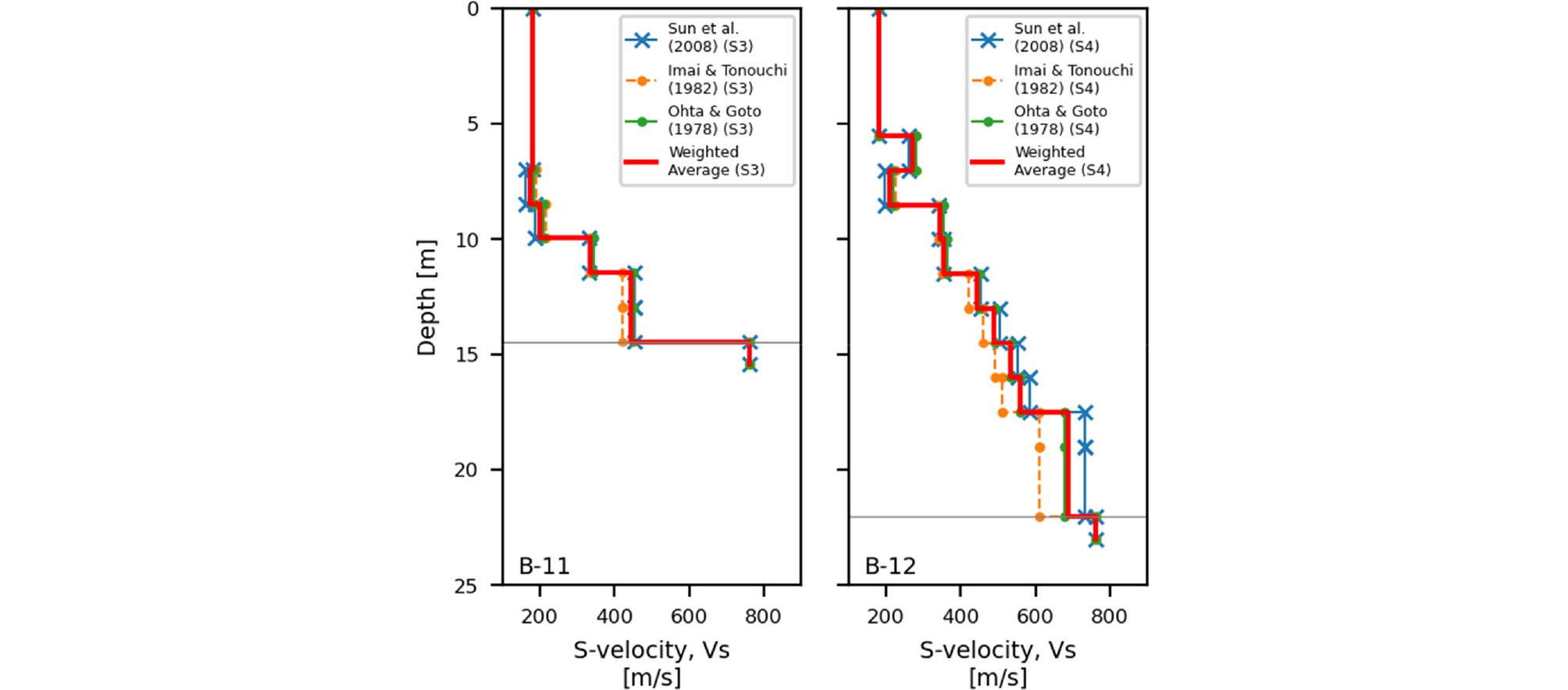
국내에서 지중구조물의 내진설계에 많이 활용하고 있는 코사인법은 이러한 단순화 가정을 기초로 지표면의 상대 변위를 산정하고 있으며 지반층의 강성(전단파속도) 구분 개수에 따라 단일 또는 이중 코사인 함수를 사용하여 전체 지반변위를 산정한다(Kawashima, 2000). 예제 지반의 전단파속도 주상도는 실제 국내 공동구 종단면도(Fig. 1) 상에서 수집한 표준관입시험값을 기반으로 구성되었다. 표준관입시험값과 전단파 속도의 상관관계에 대해 국내 지반을 모델로 한 Sun et al.(2008)과 국내 실무에서 일반적으로 사용하는 일본 연구자들의 식(Imai and Tonouchi, 1982; Ohta and Goto, 1978)에 가중치를 부과한 평균값을 사용하여 단순화 가정법에 적용할 전단파속도 주상도를 산정하였다(Fig. 2).

Fig. 1

A section of utility tunnel located in recently developed vicinity. Three locations of utility tunnel are selected as example sections in this study. While there is no fill at B-2, new fill is required to level up to the proposed street level at B-11 and B-12

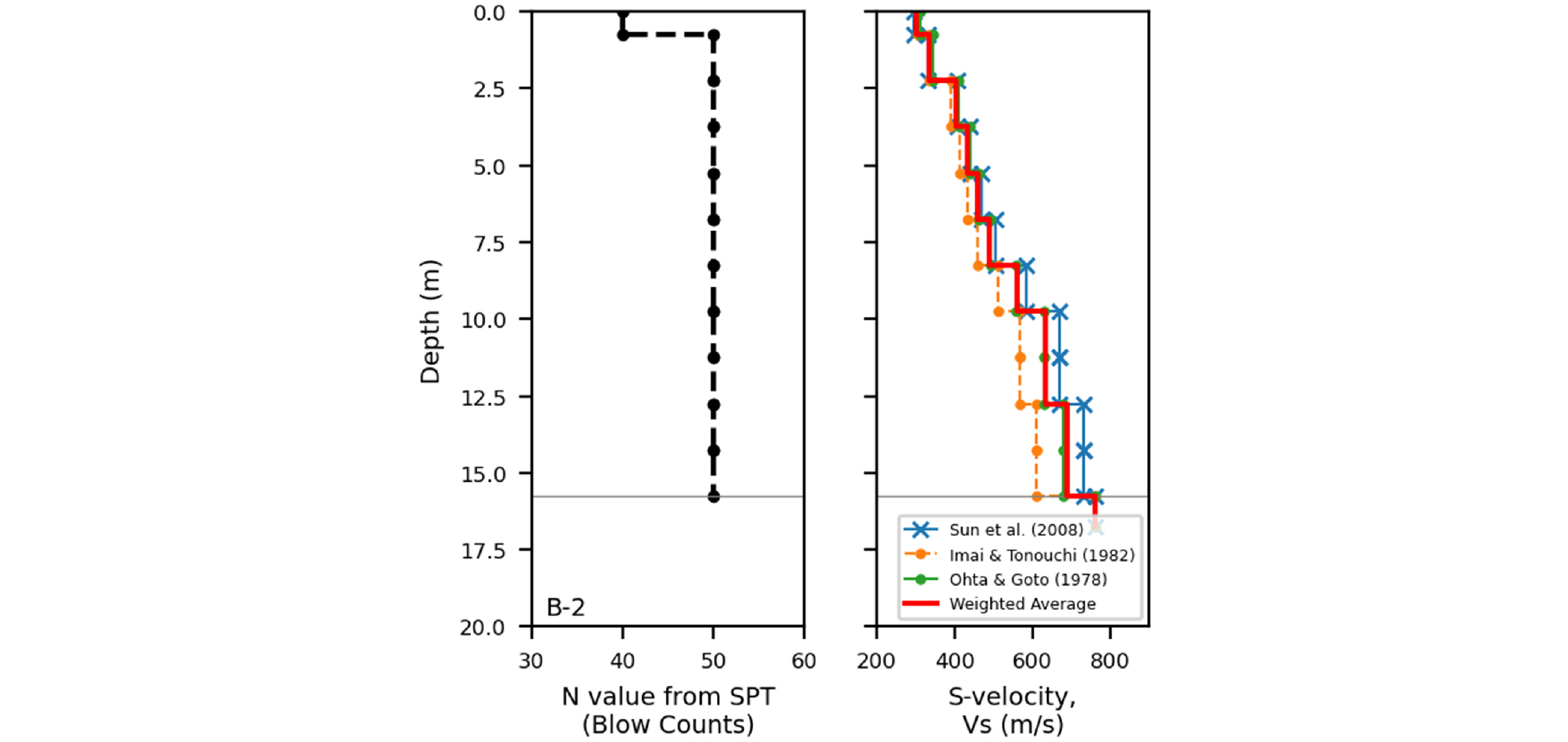
Fig. 2

Uncorrected N-value profile from in-situ Standard Penetration Test (SPT) and shear wave velocity profile at B-2 location. The corresponding shear-wave velocity (V_s) is derived from three SPT-V_s correlation models. The V_s profile would have Imai and Tonouchi (1982), Ohta and Goto (1978) with weights of 0.25 and Sun et al. (2008) with a weight of 0.5

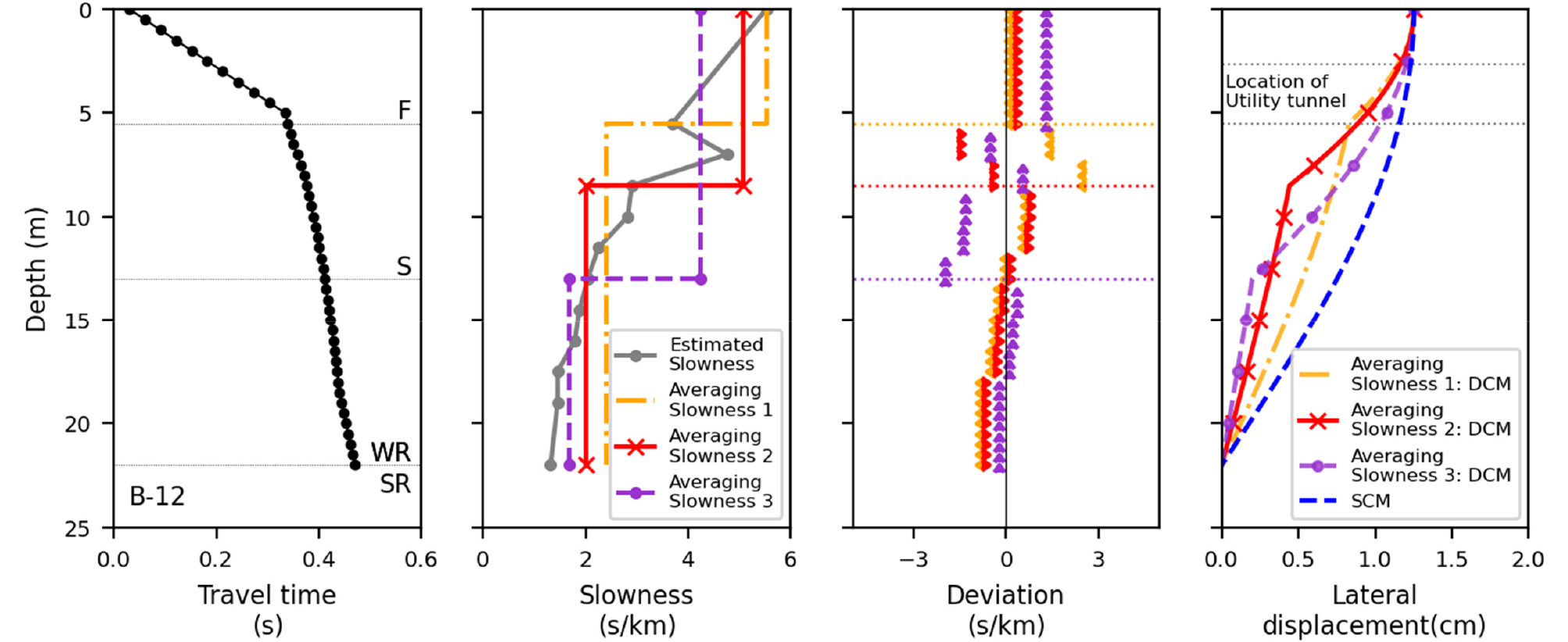
대상 예제 공동구 B-2 지점의 지반주상도에 대하여 단순화 가정법을 적용한 지반변위 산정 절차는 Fig. 3과 같다. 본 연구에서는 이중 코사인법에서 요구되는 지반층 구분 시, 전단파속도 또는 전단파속도의 역수(slowness, 1/V_s)에 대하여 추가적으로 검토하였으며, 그 외에는 기존 시설물(공동구) 내진성능 평가요령(KISTEC, 2020)에 따라 코사인법을 적용하였다.

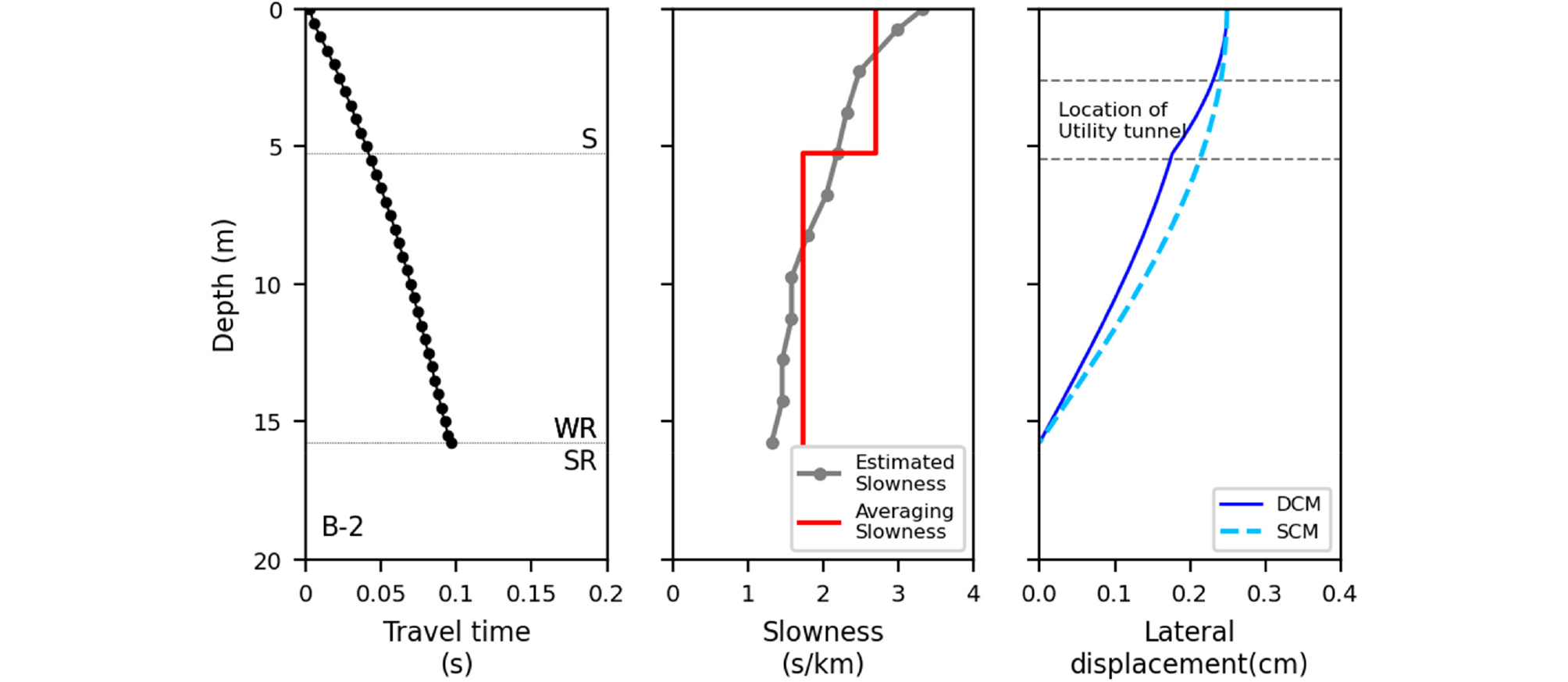
Fig. 3

The procedure of simplified ground displacement estimation; travel time, averaging slowness for Double Cosine Method, deviation, and the displacement of soil medium by Single and Double Cosine Methods (SCM and DSM) at B-2 section. The soil layers for DCM are determined by shear-wave slowness as well as the available geological information. A estimated slowness differs from an averaging slowness by deviation

해당 단면은 공학적 암반의 심도가 얕으며 단단한 지반으로 국내지반 분류상 S₂에 해당하며, 단일, 이중 코사인법에 의한 지표면에서의 변위는 공통적으로 0.25cm이다. 이는 두 코사인법 모두 동일한 지표면의 변위를 가정하고 있기 때문이다. 공동구 구조물 상부와 하부 슬래브 심도에서 단일 코사인법에 의한 지반변위는 각각 0.24cm, 0.21cm, 이중 코사인법에 의한 지반변위는 0.23cm, 0.17cm로 산정되었다. 단일 및 이중 코사인법에 의한 공동구가 설치된 심도에서의 구조물 횡단면 상·하부 슬래브 심도의 상대변위는 각각 0.03cm, 0.06cm로 매우 작은 값을 갖는다.

2.2 지반응답해석

앞서 살펴본 단순화 가정법보다 향상된 방법으로 지반응답해석법이 있는데, 이는 지반을 구성하는 다양한 층의 동적 물성값을 기반으로 암반 지반운동에 대한 대상 부지 고유의 각 지반층의 응답을 예측하는 방법으로 실제 이 지반응답해석은 국내 지반분류를 결정하는 방법으로 제안되었다(Cho et al., 2016). 본 연구에서 지반응답해석은 가장 일반적으로 사용되는 1차원 등가선형해석을 의미한다. 지반응답해석은 실제 대부분의 지반에 해당하는 비균질 지반층을 갖는 부지에 대해서 단순화 가정법보다 정확한 예측이 가능하다. 하지만, 지반응답해석은 단순화 가정법에 비해 복잡하며, 대상부지의 지반층을 구성하는 각 지반층의 동적 물성 모델과 그 선정에 따른 변동성을 포함한다.

지반응답해석법을 단순화 가정법의 결과와 비교해보기 위해서 일반적인 토사지반인 예제 공동구의 B-2, B-11, B-12 지점에 대해 지반응답을 수행하였다. 예제 공동구 구간에서 표준관입시험 값 자료가 있는 지점 중에 취약한 구간이 걸쳐진 곳인 B-12와 이에 대비되는 곳인 B-2, 그리고 B-12와 유사한 지반구성을 보이나 국내지반분류 체계상 구분하고 있는 20m 이상과 20m 미만의 공학적 암반 심도에 따른 차이를 살펴보기 위하여 B-11을 추가하여 세 지점을 선정하였다. 앞서 살펴본 B-2 지점(Fig. 2의 지반주상도와 마찬가지로 표준관입시험값과 전단파 속도의 상관관계에 가중치를 주어 B-11과 B-12 지점 각 지반층의 전단파속도 주상도를 구성하였고 이는 Fig. 4와 같다. 국내외 지반응답 실무에서 일반적으로 사용하는 절차에 따라 암반에서 계측된 지진파를 입력지반운동으로 사용하였다. 국내 암반 지반의 정의는 KDS 17 10 00(MOLIT, 2018) 따르면 전단파속도 760m/s 이상을 가진 공학적 암반을 의미하지만 이와 함께 초기 선형 증감계수, 진원거리, 가용주파수대역 등을 고려하여 후보 지반운동의 범위를 확대하기 위해 NEHRP(BSSC, 2009)의 지반분류체계 이전의 Geomatrix(EPRI, 1993)의 암반지반분류 또한 부분적으로 참고하여 전단파속도를 650m/s까지 확대하였다. 국내 지반모델(Kim and Choo, 2001; Kim et al., 2004)과 일부 매립토와 공학적 암반에 대한 일부 해외 모델(Darendeli and Stokoe, 2001; Schnabel, 1973)을 적용하여 지반응답에 사용한 각 지반의 동적 물성을 결정하였다. 이러한 지반의 비선형 응답을 산출하기 위하여 Strata 프로그램(Kottke and Rathje, 2008)을 사용하여 등가선형 지반응답해석을 수행하였다. 각 지반층의 응답은 선형탄성해석을 통해 도출되며, 이때 반복적인 계산을 통해 지반변형률에 상응하는 지반층의 비선형 동적 특성에 대한 등가의 선형 근사치가 산정된다.

Fig. 4

Weighted shear wave velocity profiles at B-11 and B-12 derived from Standard Penetration Test. B-11 and B-12 are classified as S₃ and S₄, respectively

단순화 가정법에서 지반변위 산정 시 주요 인자인 대상 지반의 주기에 상응하는 의사스펙트럼가속도(pseudo spectral acceleration, S_a) 또는 의사스펙트럼속도(pseudo spectral velocity, S_v)에 대해 암반기록 지진파가 과도한 변동성을 가지지 않도록 예제 공동구의 단면의 토사층 주기를 고정주기로 정하고, 이 주기에 대한 국내 지반분류 S₁ 설계스펙트럼 값에 각 지진파를 선형증감(amplitude scaling)하였다. B-2, B-11, B-12의 토사층의 주기는 각각 0.16초, 0.33초, 0.35초이며 상부 30m의 전단파속도 분포의 평균을 사용하는 NEHRP 지반분류(BSSC, 2009)에 따르면 C, D, C에 해당한다. KDS 17 10 00의 지반분류에 따르면 이들은 각각 S₂, S₃, S₄로 분류된다. NEHRP 지반분류와 마찬가지로 유사한 토사층의 주기를 갖는 지반이라 하더라도 다른 유형의 지반으로 분류될 수 있으며, B-11과 B-12가 서로 다른 지반으로 분류된다. 지반응답에서 B-2 단면에서는 0.16초, B-11와 B-12에서는 0.34초를 고정주기로 암반기록을 선형보정하였다. 여기서 고정주기로 사용한 토사층 단면의 주기는 공동구 지침(KISTEC, 2020)에 따라 토사층 주기에 대해 1.25배로 증가된 값이며 실제로 지반변위 산정에 사용되는 스펙트럼 값은 이 증가된 주기에 상응한다. 총 19개의 선정된 입력지반운동을 두 고정주기에 대해 선형증감한 지진파가 선보정 되었으며 고정주기에서 응답스펙트럼 값은 KDS 17 10 00 S₁ 지반의 설계응답스펙트럼값과 동일하도록 설정하였다(Fig. 5).

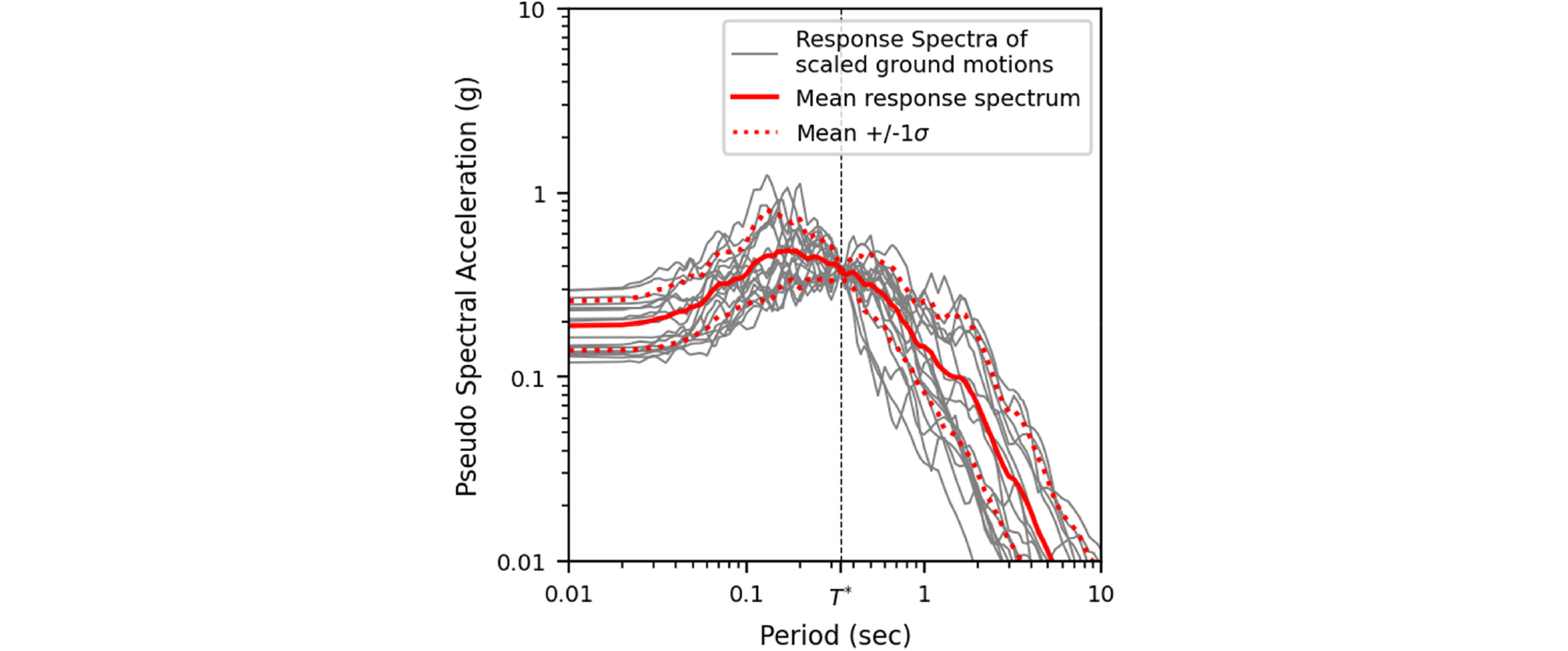
Fig. 5

Scaled ground motions (GMs) selected for site response analysis based on KDS 17 10 00 design spectral ordinate. The referenced engineering rock motion is based on KDS 17 10 00 design spectrum (S₁, PGA=0.154g). The scaled GMs are anchored at 0.34s (T^*), which is the geomean period of two soil profiles for the utility tunnel sections, B-11 and B-12

Fig. 6은 각 관심 지점에 대해 단순화 가정법과 지반응답해석을 사용한 지반변위 결과를 보여준다. 여기서 단순화 가정법에 따른 변위 산정 시 감쇠비는 5%로 재산정하였으며 이에 대한 설명은 뒤의 토론에서 상세히 다루고 있다. 지반응답해석은 시간이력해석이므로 그 결과는 시간에 따라 변화하는데, 본 연구에서는 심도에 따른 최대 지반변위를 추출하였다. 토사층 지반주기와 이에 상응하는 설계스펙트럼 값이 가장 작은 B-2의 지반의 경우 감쇠비 재산정에 따른 지표면에서 변위는 코사인법 적용 시 0.44cm인데 비해서 지반응답해석 시 평균 0.11cm로 코사인법이 4.2배 이상 큰 예측값을 가진다. 마찬가지로 공동구 구조물이 위치한 심도에서는 이중코사인법 적용 시 상·하부 슬래브 위치에서 0.41cm, 0.31cm, 지반응답해석 시 평균 0.1cm, 0.08cm로 지표면의 변위 결과와 유사한 차이를 보여준다. 공학적 암반의 심도가 상대적으로 깊은 B-12의 경우에는 지표면에서 변위는 코사인법 2.23cm, 지반응답 평균 0.69cm로 코사인법이 3.2배 이상 큰 값을 가진다. 공동구 구조물이 위치한 심도에서는 이중코사인법 적용 시 상·하부 슬래브 위치에서 2.07cm, 1.58cm, 지반응답해석 시 평균 0.64cm, 0.42cm로, 이중코사인법이 3.5배 정도 큰 값을 가진다. 이중코사인법과 지반응답해석을 사용한 지표면 변위 산정 결과는 B-2, B-11, B-12 지점에서 0.34cm, 1.25cm, 1.54cm로 지반층을 구성하는 지반층의 종류가 다양할수록 큰 차이를 나타낸다. 이러한 차이는 단순화 가정법이 실제 지반층에 대한 조건을 과도하게 단순화하였기 때문이다. 동일한 주상도에 대해서는 지표면에 가까울수록 차이가 더 큰 경향이 나타남을 확인할 수 있다.

Fig. 6

Site displacement profiles at B-2, B-11, and B-12 sections using 1-D equivalent linear site response analysis and simplified methods (single- and double cosine approximation). The response displacements in the simplified methods are calculated based on 5% damping (See Section 4.2)

대상 부지에 대한 지반응답해석 결과에서는 앞서 살펴본 단순화 가정법과 비교하여 과대 평가된 지반층의 변위가 도출되지 않는다. 살펴본 세 지점 모두 코사인법에 비해 지반응답해석에서 지표면 및 공동구 심도에서 상대적으로 작은 변위가 산출되며, 단순화 가정법이 크게는 4배 가량 과대평가하는 것을 알 수 있다. Park et al.(2010)은 국내 실측 지반의 전단파 주상도에 대해서 코사인법과 1차원 지반응답해석을 수행하여 얻어진 지반변위를 비교하였으며 실제 지반의 전단변형률의 변화율 산정 결과가 균일층 지반으로 가정한 단순화 가정법과는 심도에 따라 매우 다르다는 것을 확인한 바가 있는데, 위의 결과는 이러한 기존 연구 결과와 일치한다.

3. 지진재해도 기반의 지반변위 산정

지반응답해석이 단순화 가정법에 비해 특정 지진파에 대한 지반운동의 증폭 또는 감쇠를 정확하게 모사할 수 있지만, 이를 위해서는 국내의 지진환경에 부합하는 입력지반운동의 선정이 선행되어야 한다. 지반응답해석은 강진지역에서 부지 특정 증폭 또는 감쇠를 예측하는 방법으로 시작되었으며, NEHRP(BSSC, 2009)와 같은 기존 지반분류에 따른 지반 유형마다 풍부한 기록 지진파 자료를 보유한 지역에서 대상 부지에 대한 입력지진파의 선정이 용이하다. 따라서 미서부와 같은 강진지역의 지진자료를 바탕으로 한 통계학적 지진모델은 설계기준의 지반분류에 부합하도록 구분될 수 있는 반면, 통계학적 기반의 지진모델이 불가능한 국내와 같은 중약진 지역에서는 지반응답해석이 그 지역의 지진환경에 부합하는 결과를 산출한다고 판단하기 어렵다.

앞서 세 지점의 대상 부지에 대해 수행한 지반응답해석에서 볼 수 있듯이 특정 지진파에 대해서 대상지반의 암반과 토사층의 지반운동 증폭 비율을 산정할 수 있지만, 이 과정에서 선정한 암반지반에 대한 입력지진파가 국내의 지진환경에 부합하지 않는다. 일반적으로 지진환경에 부합하는 지진파의 선정에는 지진원 특성 모델과 지반운동 모델, 이와 관계된 불확실성에 대한 정보가 요구된다. 미서부의 경우 활성지각지역(active crust regions)의 천부지각 지진 모델을 사용하며, 이러한 모델은 대상지역의 지진원 특성에 따른 규모, 거리, 발진기구(focal mechanism) 외에도 얕은 심도에서의 지반증폭, 분지효과, 진앙깊이, 단층 경사와 상반 효과(hanging wall effect) 등 많은 조건을 고려하고 있다. 앞에서 논의한 지반응답에서 적용한 입력지반운동은 모두 천부지각 지진 모델인 NGA-West2(Ancheta et al., 2013) 자료를 사용하였으며, 지반응답해석을 위한 적합한 암반지진 기록의 부족으로 인해 국내의 지진환경과는 매우 다른, 섭입대 지진파 등도 입력지진파에 포함되었다. 부지 특정 지반응답해석 시, 입력지진파 선정에 근본적으로 충족되어야 하는 조건이 있는데, 대상 지반의 지진환경에 부합하는 지진원, 거리, 단층 유형, 그리고 관심 주파수 대역의 포함 여부 등이다. 이 때문에, 공학적으로 의미있는 규모의 지진파 기록이 매우 적은 곳에서는 기존 지진파를 사용한 지반응답해석 수행 시 많은 제약이 있다. 실제 입력지진파로 요구되는 암반 기록 중에 국내의 지진환경에 부합하는 근거리의 암반 기록은 전 세계적으로 매우 희귀하기 때문에 합리적인 결과를 도출하기에 어려움이 있다. 이러한 제약을 극복하기 위해서는 다양한 주파수 대역을 가진 입력지진파의 개수를 늘리는 방법이 있으나 실무적으로 비용이 증가하며 여전히 지진원 특성에 적합하다고 볼 수 없다. 국내의 경우도 대부분의 중약진 지역과 마찬가지로 축적된 지진동 정보가 극히 제한적이라는 점이 해석 과정에서의 주된 어려움으로 지적되고 있으며, 중약진 지역의 지진동 특성에 부합하지 않는 입력정보의 사용은 구조물의 실제 거동과 손상 정도에 대한 잘못된 이해를 낳을 수 있다. 실제 해외 중약진 지역 원자력시설물의 내진 평가는 대상 지역의 재해도에 상응하는 지진원 모델을 적용하여 지각구조를 포함한 지반응답을 통해 수행되고 있다(Biro and Renault, 2012; Rodriguez-Marek et al., 2014). 본 연구에서는 기존 응답변위법의 이러한 단점을 보완하며 동시에 국내 지진재해에 부합하는 지반의 변위산정 방법을 제시한다.

3.1 국내 지진모델

강진지역의 지진재해도는 풍부한 지진기록 자료를 바탕으로 통계학적으로 유도된 감쇠식(지반운동예측식, attenuation relationship) 모델을 기반으로 작성되지만, 국내나 미동부와 같이 지진기록이 부족한 지역에서는 지진학적 모델을 바탕으로 추계학적으로 강진동을 모사에 기반한 방법이 널리 사용되고 있다. 국내 감쇠식 모델은 대부분이 추계학적 강진동 모사에 의한 방법에 의존하고 있으며, 연구자마다 국지적 특성을 반영하는데 집중하고 있다. 이는 국내 지진모델이 국내 원전부지가 집중적으로 위치한 한반도의 남동부 지역에 대한 재해도 산정을 목표로 발전되어 왔으며, 이러한 목적을 위해 효율적으로 지반운동을 모사하는 방법인 추계학적 방법(stochastic method)을 주로 사용했기 때문이다.

추계학적 강진동 모사는 고주파 대역의 지반운동을 지진원과 지진파의 전달 양상에 대한 지진학적 모델에 의해 결정되는 필터를 통해 생성된 임의의 가우시안 잡음(Gaussian Noise)을 사용해 구현한다. 이 방법에서는 지반운동의 진폭 스펙트럼을 매개변수로 사용한 함수의 형태로 고주파 대역의 강진동을 모사할 수 있으며, 지진 규모와 지진원 거리에 종속된 강진동의 지속시간 동안 지진동의 불규칙 위상 스펙트럼과 조합하여 공학적 관심 영역인 1Hz 이상의 고주파 대역의 지반운동을 모사하는 데 특히 유용하다. 이 방법은 국내와 같이 잠재적 피해를 유발할 수 있는 지진(규모 5 이상)에 대한 정량적 기록이 부족한 지역의 지진을 예측하는 데 널리 사용되고 있다. 추계학적인 강진동 모사의 주요한 특징은 지진의 발생 과정과 지진파 전달에 대한 지구물리학적 측면에서 연구된 결과를 간략한 함수 형태로 추출할 수 있다는 점이다. 지진원에 대해서는 점진원 모델, 유한 단층 모델 등을 포함하여 다양한 모델이 사용되고 있지만, 동일한 추계학적 방법을 기반으로 하고 있다. 지진환경에 부합하는 지진원 모델의 추계학적 모사 방법과 모델을 구성하는 다양한 인자에 대해서는 Silva et al.(1997)과 Boore(2003)에서 보다 상세히 살펴볼 수 있다.

3.2 지진 시나리오 산정

재해도에 상응하는 지진하중의 산정에 있어서 지진 규모와 발생 거리의 조합과 함께 대상지반의 단층 종류 등 현대 지반운동 예측식에 포함되는 다양한 인자를 고려하여 여러 시나리오를 가정할 수 있다. 국내의 경우 유효지반가속도 지도로부터 지진재해도의 deaggregation 정보를 얻을 수 없으므로, 국내 대상 부지에 대해서 재현주기에 따른 지진 규모-거리 조합 중 최대빈도에 대응하는 시나리오 지진을 확률론적 지진재해 deaggregation을 통해 산정할 수 없다. 하지만, 대부분의 중약진 지역의 재해도와 마찬가지로 국내의 경우 특정 부지의 지진재해도를 지배하는 대표성을 가진 지진을 결정하기 어렵다. 즉, 특정한 소수의 지진원 대신 무수히 많은 규모-거리 조합을 가진 지진이 연간초과확률에 따라 지진재해도에 영향을 준다는 것을 예상할 수 있다.

본 연구에서는 시나리오 지진을 선정하고자 대상 공동구의 설계 응답스펙트럼 값에 해당하는 다양한 지진 시나리오에 대해 추계학적 강진동 모사를 통한 규모와 거리의 조합을 우선 산정한다. 예를 들어, 공동구 단면 B-12의 토사층 지반주기에 상응하는 설계응답스펙트럼 값에 해당하는 규모와 거리의 조합을 계산하면 규모 5.5와 6.5 지진의 경우 단층 파열면에서부터 부지까지의 최단거리를 각각 약 10.3km, 23.5km로 산정할 수 있다. 공학적으로 피해를 유발하는 판내부 지진으로 이 두 지진은 대상 주기(T=0.34초)에서 모두 약 0.57g의 스펙트럼 값을 가진다(Fig. 7). 대상주기에서 동일한 스펙트럼 값을 갖도록 모사된 두 지진의 경우 규모가 큰 지진이 상대적으로 작은 최대지반가속도를 가지는 반면에 장주기에서는 보다 큰 스펙트럼 값을 가진다. 동일 거리에 대한 지진의 비교를 위해 규모 6.5 지진을 Fig. 7에 추가하였고, 규모 5.5 지진과 동일거리(10.3km)에서 발생하는 규모 6.5 지진은 최대지반가속도 1.0g를 가지는 것으로 나타난다.

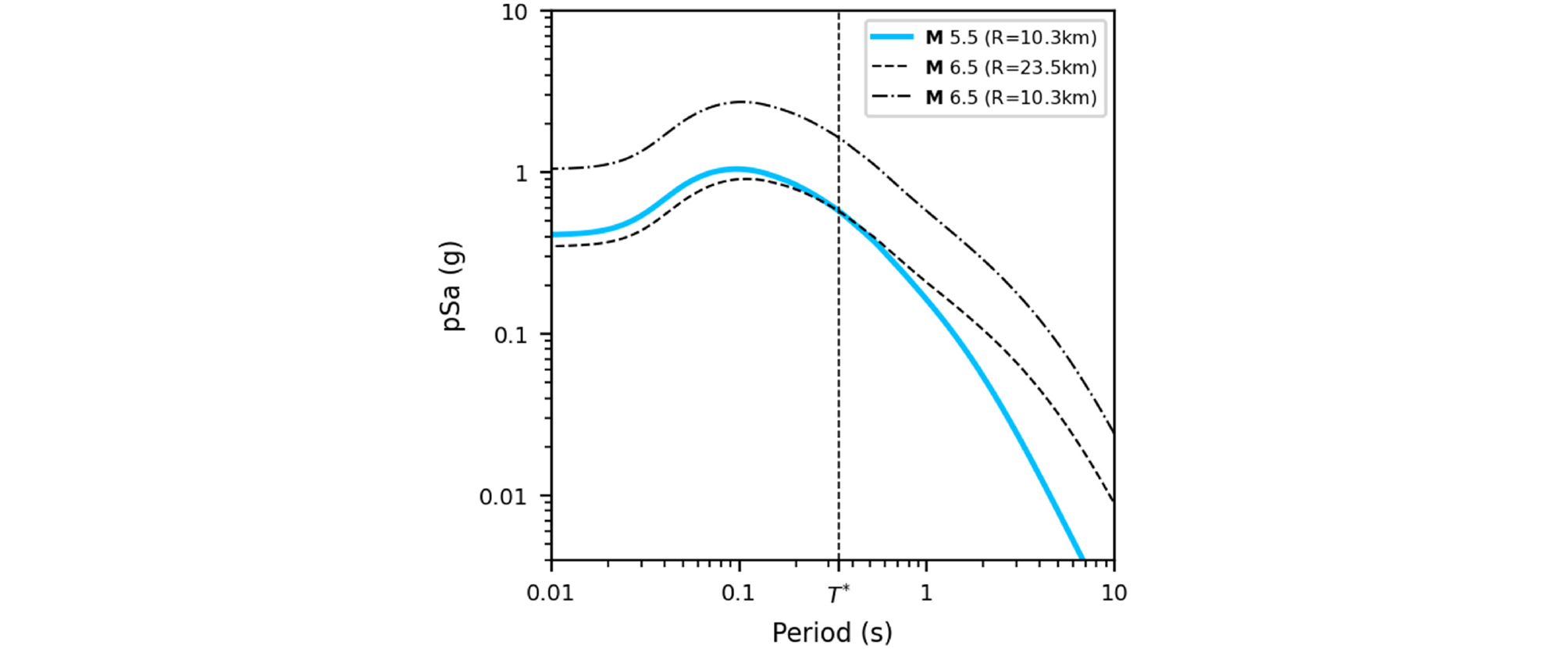
Fig. 7

5%-damped response spectra of scenario earthquakes using stochastic method. A generic soil model is developed for computing amplifications on S₄ profile. Two scenario earthquakes have the same spectra acceleration at the target period (T^*=0.34s). M 6.5 earthquake with rupture distance of 10.3 km is plotted for comparison purpose. The distance means the distance from the rupture plane. SMSIM (Boore, 2005) is employed for simulating ground motions

국내의 지진재해도는 해외의 경우와 같이 재해도 산정에 대한 상세한 자료를 제공하고 있지 않으며(NEMA, 2013; KIGAM, 2012), 그 결과 적합한 시나리오 산정에 요구되는 대상 부지의 지진재해도를 지배하는 지진원을 특정화할 수 없다. 국내 공동구 내진설계에서는 안전성 검토에 적용하는 100년에 10% 초과확률을 가진 지진하중을 구성하는 재해도(연간 초과빈도 1.0×10^-3)를 사용하고 있으며 일반적으로 공학적 관심의 대상이 되는 연간 초과빈도 2.0×10^-3와 4.0×10^-4 사이의 재해도에서 원거리 지진(Fig. 8의 규모 6.5, 거리 23.5km)은 상대적으로 큰 초과확률을 가진 재해도 수준에서 큰 영향을 미치지 못한다. 따라서 본 연구에서는 국내 공동구 지침에 상응하는 붕괴방지 수준의 평가를 위해 판내부 지진환경에서 충분히 빈번한 빈도로 발생 가능한 규모 5.5 지진, 거리 10.3km의 경우를 설계응답스펙트럼에 상응하는 대표 시나리오로 선정하고 공동구가 위치한 일반화된 지반층 모델에 대해서 지반의 응답변위를 산정한다.

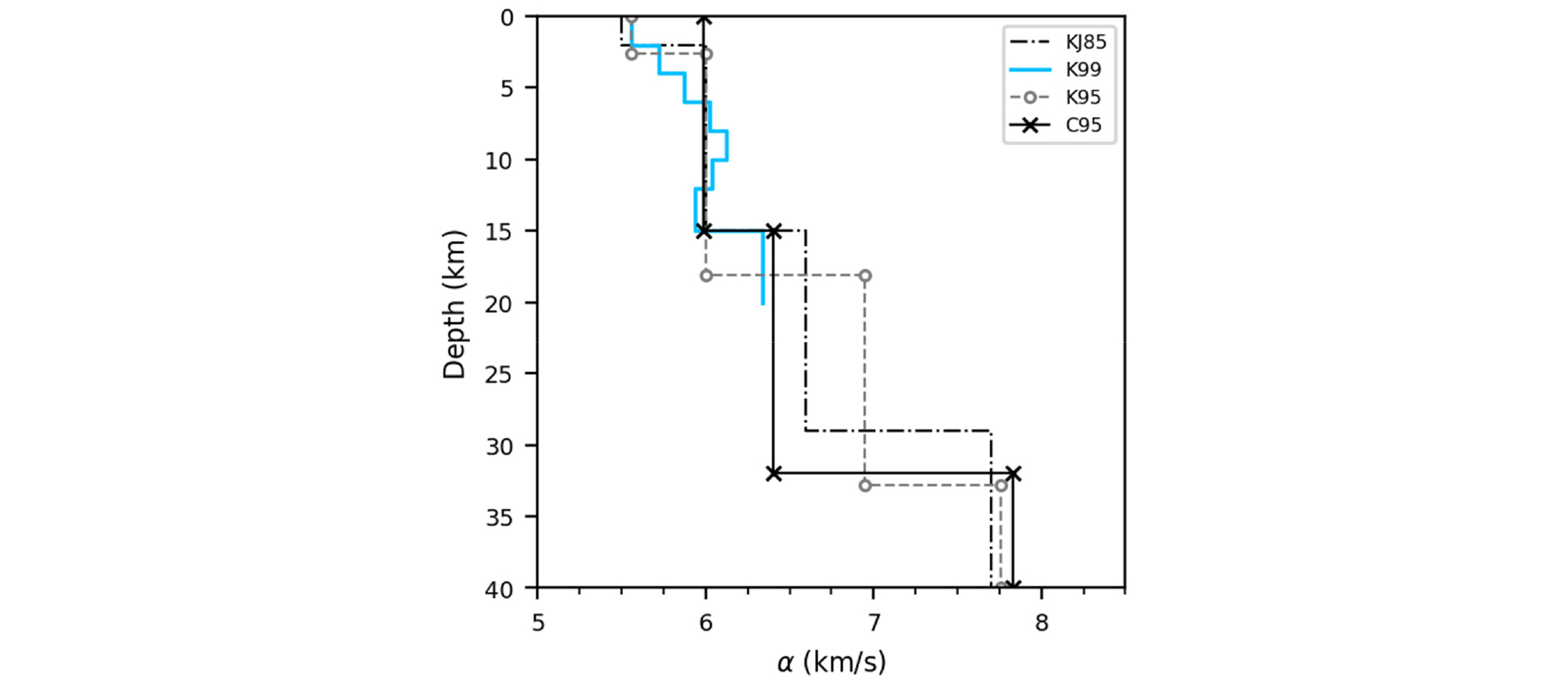
Fig. 8

P-wave velocity (α) versus depth to 40km. The stochastic method used in this study use crust depth to 10km. (KJ85= Kim and Jung, 1985; K95= Kim, 1995; C95= Chung, 1995; K99= Kim, 1999). Some of models consist of very simple profiles of crust structure extending to 40km, while K99 has detailed structure extending down to the depth of 20km

3.3 지반모델

지반운동예측식에 사용되는 지반은 일반적으로 매우 단단한 암반 또는 공학적 암반을 기준으로 하고 있으며, 이에 따라 기준이 되는 암반(V30=760m/s)에 대해 감쇠식의 보정이 수행되었다. 국내외 설계기준은 특정 전단파 속도에 해당하는 지반을 공학적 암반으로 정의하고 이를 기반으로 분류체계가 구성되어 있다. 이는 강진지역의 통계적 초기 감쇠식 모델이 크게 암반지반 또는 토사지반의 두 가지 조건으로 구분한 것과 맥을 같이한 것이며, 이후 내진설계의 세분화된 지반분류 체계에 기반이 되는 NEHRP 분류기준의 B-C 지반 경계값(V30=760m/s)에 맞게 수정되었다.

지반운동예측식을 유도할 경우 또는 설계기준의 분류체계에 따른 지반과 같이 일반화된 지반조건에 대하여 모사할 경우, 1차원 지반응답해석과 같은 특정 대상 부지의 고유 증폭에 대한 상세한 계산보다는 다양한 변동성을 고려한 지반의 응답이 더욱 적합할 수 있다. 본 연구에서 지반변위 산정을 위해 제시하는 추계학적 강진동 모사를 통한 방법에서는 지각을 포함한 일반화된 지반모델이 요구된다. 시나리오 지진 산정에 사용된 추계학적 강진동 모사를 통해 생성되는 지반운동은 일반적으로 심도 5km 이상인 진원에서 지표면까지 도달하는 과정에서 전달경로, 지각 및 지반효과에 의해 증폭 및 감쇠를 거쳐 최종 산정된다. 예를 들면, 앞에서 살펴본 공동구 B-12 지점을 포함하는 일반화한 토사지반의 경우 국내 내진설계기준의 지반 분류체계상 깊고 단단한 지반인 S₄에 해당하며 이에 대한 일반화된 토사지반 모델을 설정한다. 추계학적 강진동 모사 방법을 통해 산출한 지진원 스펙트럼은 구조물에 큰 영향을 미치는 얕은 심도 뿐만 아니라 지각을 거치면서 증폭과 감쇠가 일어난다. 본 연구에서는 이러한 점을 고려하여 지진원 심도로부터 대상 부지까지 지각을 포함한 일반화된 토사층 지반모델을 구성한다. 이를 통해 다양한 지반을 일반화한 지반변위 산정이 가능하다.

공동구 지반조건 예시로 토사지반을 다루는 이유는 일반적으로 지하공동구가 신설되는 위치가 신도시로 개발되는 택지와 그 인근이며 이러한 경우 국내 지반환경 조건상 대부분이 토사지반인 점을 반영한 것이다. 또한, 개착식으로 시공되는 지하공동구의 되메우기에 사용되는 매립토 등은 상대적으로 연약한 토사로, 대상 부지는 대부분 토사지반으로 분류되기 때문이다.

국내 대부분의 추계학적 모델에서는 대표 암반(또는 공학적 암반)이나 일반 토사 등의 구분을 하지 않거나 이에 대한 조건을 명확하게 특정하고 있지 않으며 이에 대한 보정에 대해 기술하고 있지 않다. 본 연구에서는 대표 지반조건(예를 들어 지반분류 B-C 경계에 해당하는 공학적 암반)에 따라 명확하게 보정된 기존의 감쇠식 대신에 일반화된 S₄지반에 대한 추계학적 강진동 모사를 적용하며, 이러한 방법으로 생성된 지진원의 강진동은 국내의 지진재해도에 부합하는 지각-지반모델을 통해 증폭된다. 참고로 최근 원전부지의 평가를 위해 개발된 지진동감쇠식(KEPRI, 2006)은 상부 30m 평균전단파 속도 600∼700m/s를 기준으로 하고 있다(personal comm. 연관희, 전력연구원).

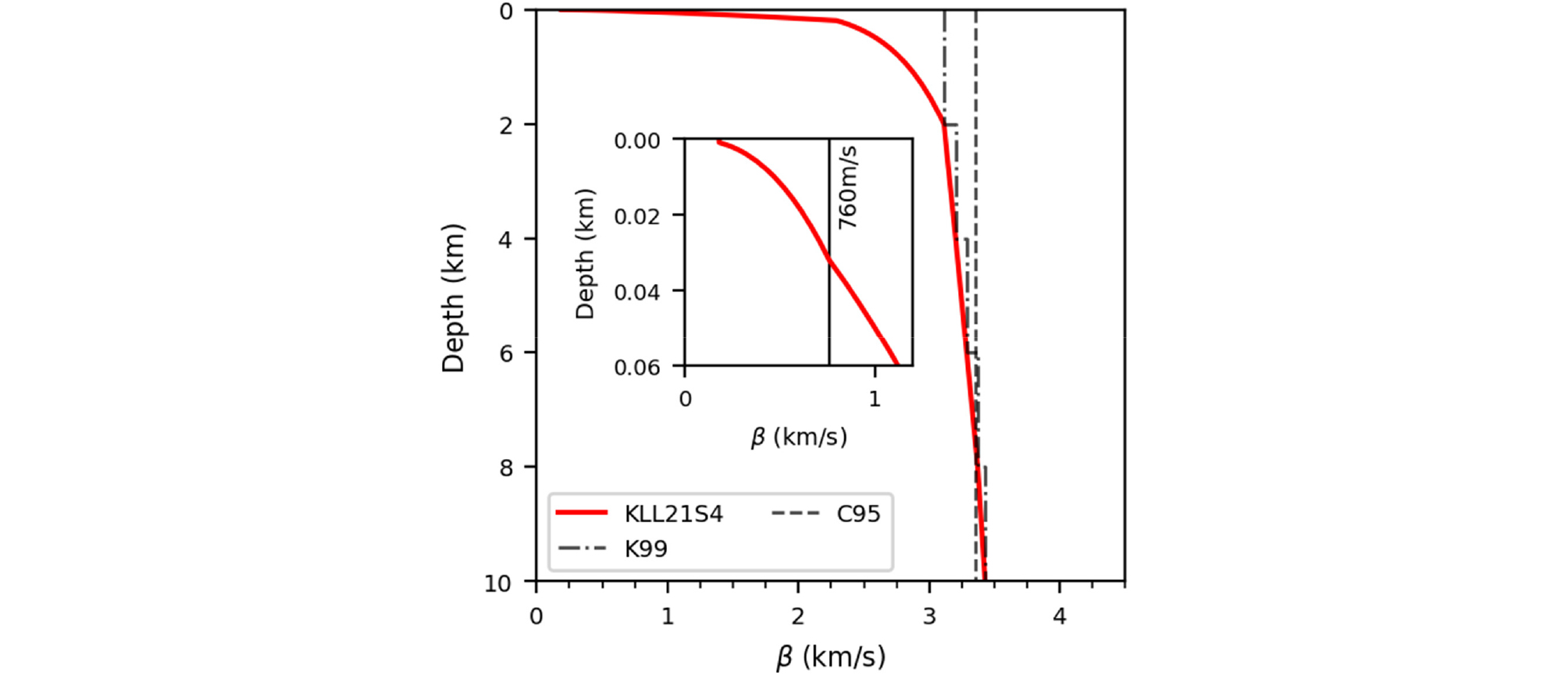
추계학적 방법에 따른 지진동 산정에 요구되는 일반 토사층의 지반모델 구성에 있어서 지각모델의 범위를 심도 10km까지로 설정하였다. 그 이상의 심도에서 지각에 의한 증폭은 공학적으로 무시할 만큼 충분히 작다. 지각모델에서 2km 이상의 심도에서 전단파속도 분포는 거의 일정한 값을 가지며, 따라서 진원 깊이 5km 이상의 천부지진에 대해서 여기서 적용한 지각모델의 보정을 최소화할 수 있다. 지반모델 구성을 위해 살펴본 4개의 국내 지각모델은 모두 유사한 구성을 가지고 있다(Fig. 8). 이중 Kim(1999)은 한반도 양산단층 지역에 대해 20km 심도까지 P파 속도(α)를 도출하였다. 비록 제안된 지각구조는 양산단층 지역으로 국한되어있지만, 정태웅(1995)이 7개의 미소 지진관측을 통해 정량적으로 제시한 한반도 지각구조에서도 상부 15km의 P파 속도는 5.99km/s로 거의 차이가 없으며 살펴본 다른 지각모델과도 큰 차이가 없다. 다만 본 연구의 관심 대상인 10km 이내의 얕은 지각구조에서 Kim(1999)의 모델이 보다 세분화된 P파 구조를 제시하고 있다는 점에서 차이가 있다. 본 연구에서 지반응답에 적용하는 일반화 토사지반의 하부 지각구조는 양산 단층 지역으로 구성된 모델을 기반으로 한다.

3.3.1 일반화 토사지반 모델

일반화 토사지반에 대한 전단파속도 모델은 두 단계의 과정을 통하여 구성하였다. 우선 부지의 심도(z)와 전단파속도(β)에 대한 관계를 설정하는 과정과, 이를 지반응답에서 일반적으로 사용하는 계단식 분포로 단순화하는 과정으로 구분할 수 있다.

첫 번째 단계에서는 지반모델의 전체 깊이를 지표면으로부터 10,000m까지로, 0∼32m(구간 1), 32∼190m(구간 2), 190∼2,000m(구간 3), 2,000∼10,000m(구간 4)의 총 4개 구간으로 나누었다. 지표면에서 심도 2,000m까지는 각 구간별 여러 분포함수 관계를 시도한 후 지수함수의 관계(β=a×z^b)로 추정한 깊이에 대한 전단파속도 분포의 연속함수를 결정하였다. 여기서 a와 b는 지정한 z와 β의 값을 만족하도록 결정된 값이다.

구간 1은 표층 구간으로 전체 부지증폭에 있어서 고주파 대역에 가장 큰 영향을 주는 심도이며 공학적 암반(V_s=760m/s) 상부의 토사층을 구성한다. 공학적 암반의 심도는 국내 S₄지반으로 분류되기 위해 20m 이하 50m 이상에 위치해야 한다. 구간 1의 경계는 암반 경계 심도의 기하평균(H_r=31.6m)을 참고로 32m를 설정하였다. 지반모델 구성에 적용한 지수함수 관계상 지표면(z=0m)에서 β=0으로 설정하는 것은 실제 지반의 물성과 부합하지 않는다. 그 대신에 지표면에서 1m 두께의 토사층은 매립토로 구성하여 β=181m/sec을 적용하였다. 이하 구간에서부터는 깊이 1m와 32m 지점을 기준으로 (z,β) 좌표계에서 (1m, 181m/sec), (32m, 760m/sec) 두 쌍의 값을 만족하도록 지수함수의 계수 a와 b를 결정하였다. 구간 2는 지각 물성과 표층과의 중간지역으로 약 200m 부근까지 확장하였다. 계단식 전단파속도 분포 구성에서 깊이에 따른 지반층의 두께 증가를 반영하여 200m 전후에서 교점의 심도로 190m가 선택되었다. 구간 3에서도 유사한 관계에 따라 전단파속도 분포를 가정하였으며, (z,β) 좌표계에서 (190, 2,292), (2,000, 3,113) 두 쌍에 대한 함수를 구하였다. 마지막으로 심도 2km 이상인 구간 4에서는 앞서 언급한 지각구조(Kim, 1999)를 기반으로 깊이 10km까지 구성하였다(Fig. 9). 이때 P파 속도를 S파 속도로 변환하기 위해 심도에 따라 변하는 지반 물성인 포아송 비와 독립된 관계로 P파 속도와 S파 속도의 비(Kim, 1995)를 사용하여 변환하였다.

두 번째 단계에서는 위에서 가정한 z와 β의 관계를 기초로 부지응답에서 사용하는 각 지반층을 구분하는 방법과 같이 계단식 β 분포로 단순화하였다. 계단 하나마다 동일한 β를 가지게 되며 각 계단의 높이는 깊이가 깊어질수록 증가하도록 하였다. 각 계단에 대응되는 β는 첫 번째 단계에서 가정한 β 분포의 평균을 사용하였다. 즉, 해당 z범위에서 위에서 가정한 모델과 계단식 모델의 면적 값은 동일하다.

Fig. 9

S-wave crustal velocity model in this study for generic S₄ soil sites. The solid line in the inset figure is the reference engineering rock velocity of 760m/s. The engineering rock depth is 32m in this soil model

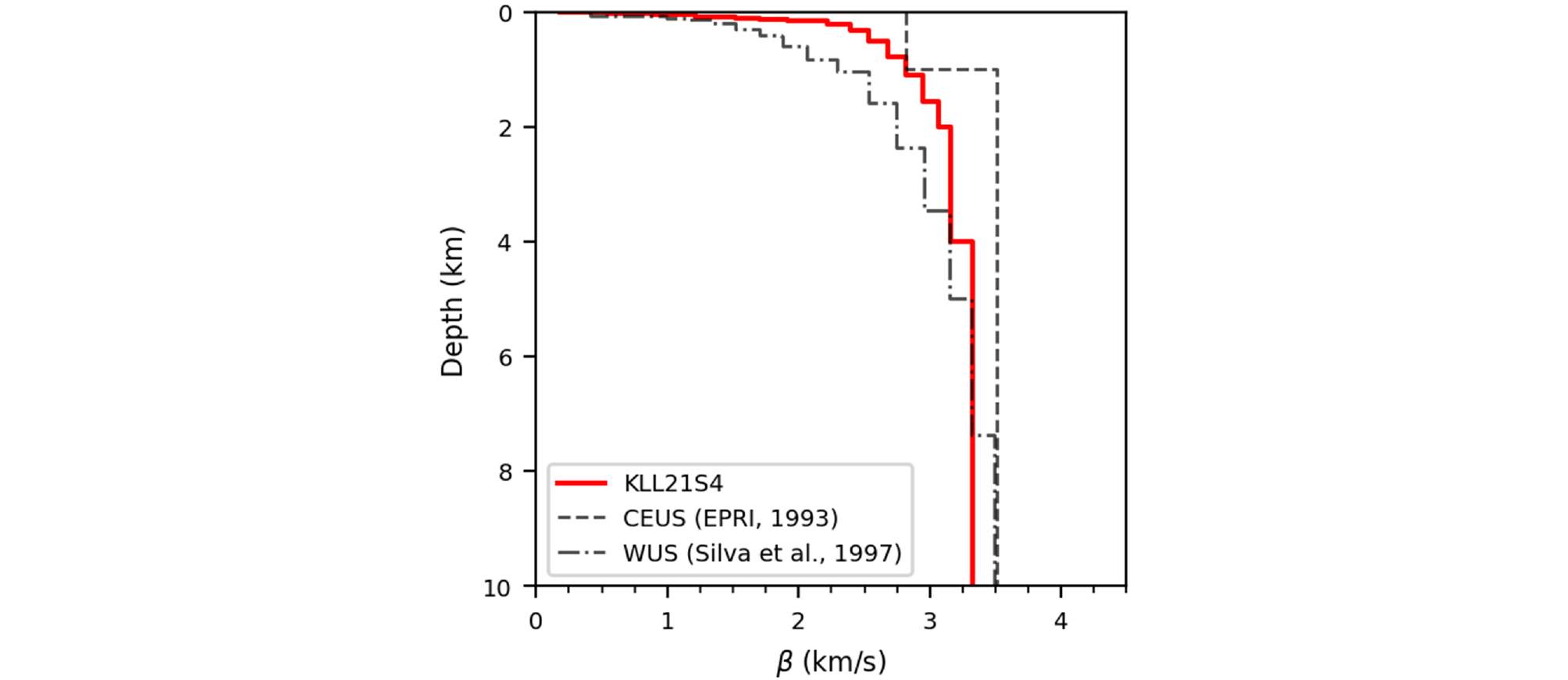
Fig. 10은 이러한 과정을 통해 구성한 일반화 토사지반 모델(이하 KLL21S4 모델)을 미서부와 동부의 일반화 암반 모델과 함께 10km 심도까지 보여준다. 상부 30m의 계단식 지반층 구분에 의한 전단파속도 분포평균(V30)은 435m/s이고, 국내지반분류 표준에 따른 토층평균전단파속도(V_s,soil)은 445m/s이다. 본 연구에서 도출한 KLL21S4 모델은 NEHRP 지반분류상 C에 해당하며, 현행 국내 내진설계기준상에선 S₄로 지반정보가 없는 경우 설계 또는 평가 기준에서 기본값으로 가정하는 지반조건에 해당한다.

Fig. 10

Stair step velocity profiles proposed for generic S₄ soil sites (KLL21S4 model) with crustal velocity profile. Average shear-wave velocity profile for Western and Eastern rock sites in North America are shown for comparison purpose

3.3.2 균질 포아송 모델(Homogenous Poisson Model)

국내 지각모델을 포함한 설계기준 상의 일반화된 지반모델을 구성하는 다른 방법으로 앞서 제시한 일반화 토사지반 모델에 추가하여 지반구성의 변동성을 고려할 수 있는 랜덤 과정(random process)을 사용한 지반모델을 구성할 수 있다. 이는 Toro(1995)에 의해 제안된 방법으로 랜덤 주상도 모델을 생성하기 위해 먼저 지반층을 구성하는데, 이때 포아송 과정(Poisson process)을 적용한다. 심도에 따라 일정한 발생 빈도를 가지면서 새로운 지반층을 생성하는 것은 균질 포아송 과정(Homogeneous Poisson Process, 이하 ‘HPP’), 심도에 따라 발생 빈도를 변화시키면서 지반층을 생성하는 것은 비균질 포아송 과정(Non-homogeneous Poisson Process, 이하 ‘NPP’)에 해당한다.

NPP의 경우 대상 부지의 지반과 그 지역을 사전 조사하여 심도에 따른 발생 빈도를 예측할 수 있도록 제시한 공식을 사용해야 한다. 국내 대상 지반분포에 대한 지반층과 전단파속도의 상관관계를 설정하기 위한 자료 분석 등의 선행 연구가 미흡한 관계로 NPP를 적용하기 어려우므로, 본 연구에서는 일정한 발생 빈도를 가지고 지반층을 생성하는 HPP를 적용하여 지반층 모델을 생성하였다. 이렇게 생성된 모델은 15개의 지반층으로 구성되도록 설정하였다.

지반층의 구성 이후에 각 층마다 전단파속도를 산정하여 전단파속도 모델을 만들어 랜덤 주상도 모델을 완성한다. 이때, 대상 지반분류에 해당하는 모델을 만들기 위해, Toro가 제시한 심도에 따른 계수들과 심도별 중간 전단파속도를 사용하여 20,000개의 전단파속도 모델을 구성하였다. 이렇게 생성된 20,000개의 전단파속도 모델을 국내 내진설계일반(KDS 17 10 00)에서 제시된 지반의 분류 방법에 적용하여 재분류하였다. 심도 30m이내의 표층 평균전단파속도가 아닌 전단파속도가 760m/s 이상인 지반층으로부터 지표면까지의 표층 평균전단파속도를 계산하여, 이를 기준으로 S₂부터 S₅로 분류하였으며, 국내 기준에 따라 공학적 암반으로 고려될 수 있는 760m/s가 등장하지 않거나, 등장하더라도 50m보다 깊은 심도에서 등장한다면, S₆로 분류하였다(Fig. 11).

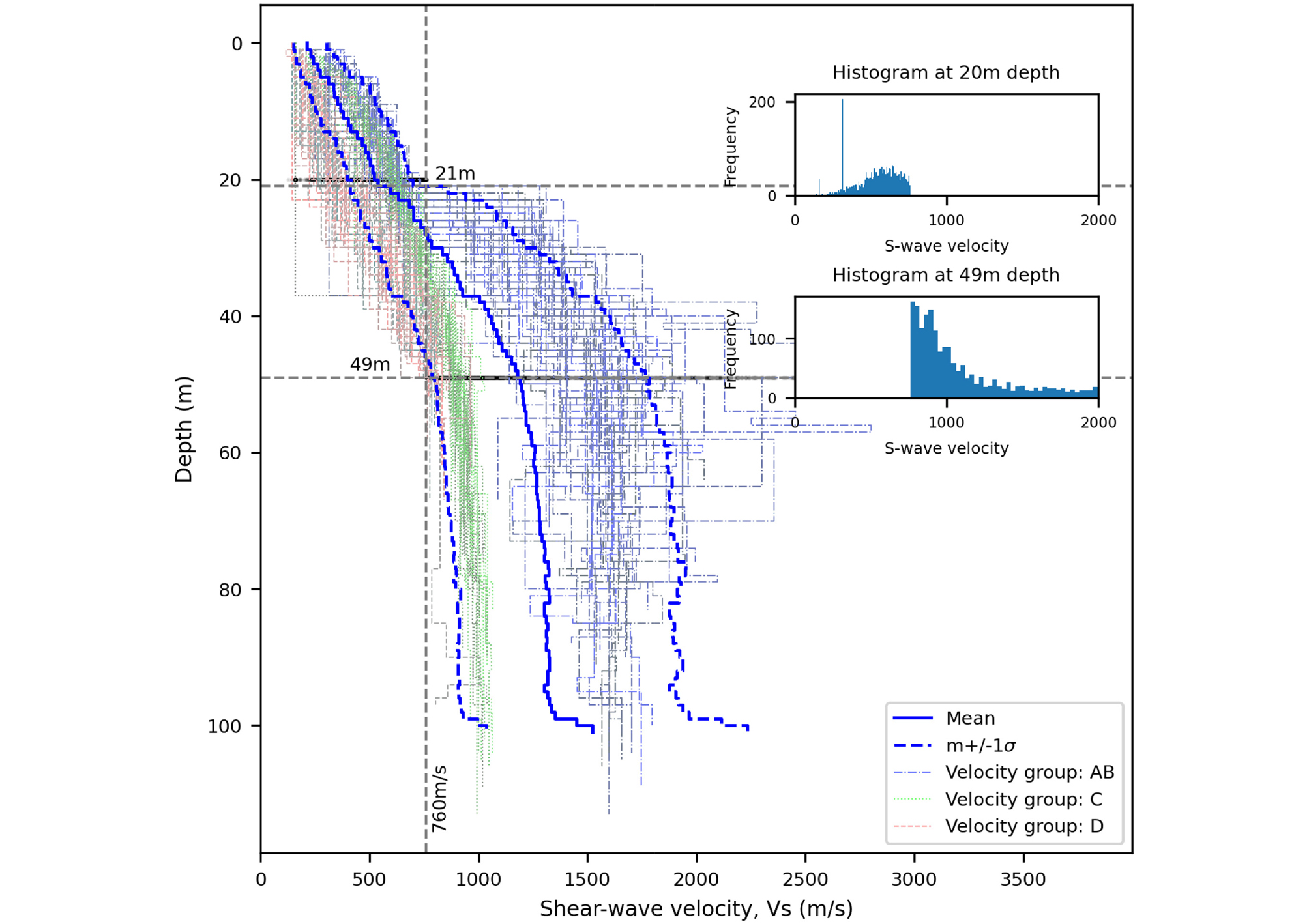
Fig. 11

S₄ soil profiles using homogeneous Poisson Processes. 4 velocity profile groups are generated by random process and the generated profiles are re-classified per Korean Seismic Code (KDS 17 10 00). Total 142 profiles are classified into S₄ (49 models from Group AB, 49 from C, 44 from D, No model from Group E)

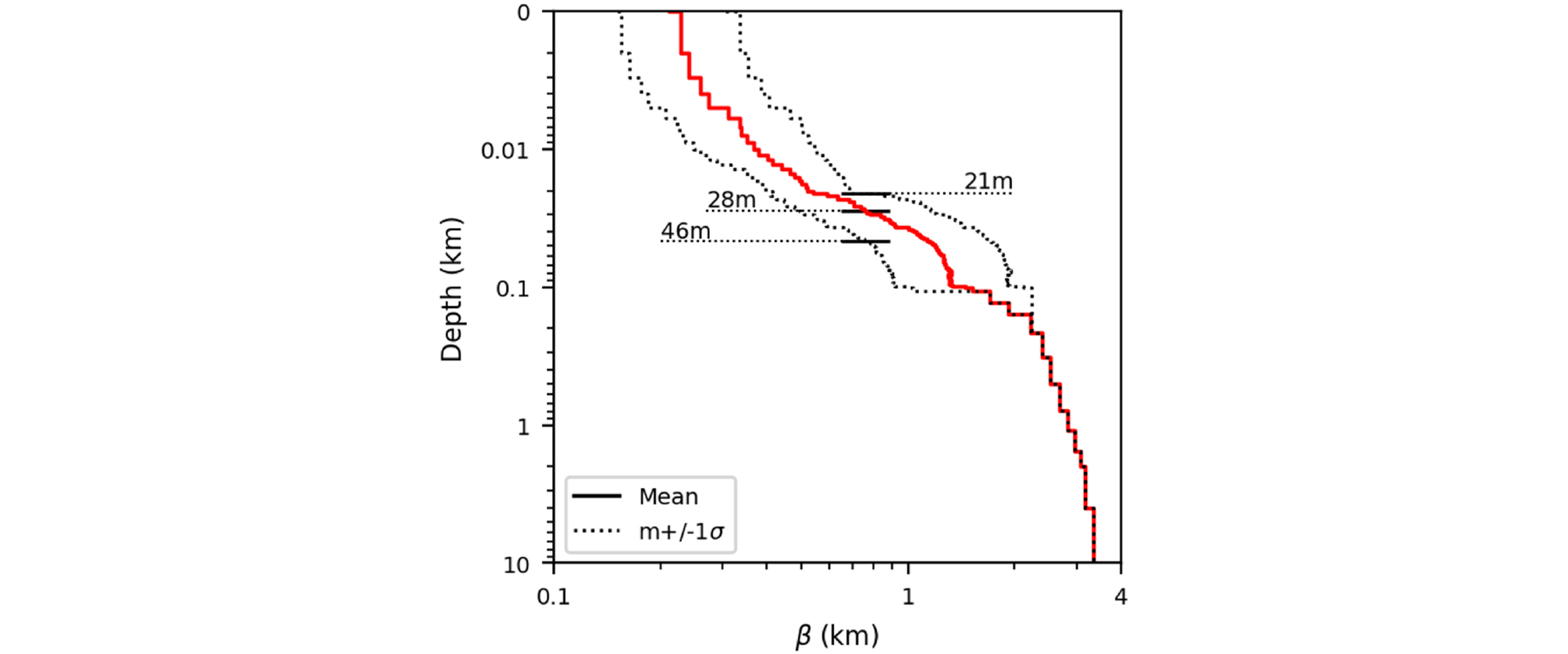
생성된 20,000개 전단파속도 모델 중 2,910개가 S₄ 토사지반으로 분류되며, 대부분 지반분류 C(매우 조밀한 토사 혹은 연약한 암반) 주상도에서부터 유도되었다. Fig. 11에서는 이러한 랜덤 과정을 통해 생성된 S₄지반의 평균과 무작위적 변동성을 고려한 표준편차를 포함한 주상도가 함께 표시되어 있으며, 평균(m)과 평균±표준편차(m±1.0σ)의 전단파속도 주상도에서 공학적 암반의 출현 심도는 각각 28m, 21m, 46m이다. 특정 심도에서 전단파속도 값의 분포를 확인하기 위해 심도 20m와 49m에서의 빈도를 나타내는 히스토그램을 Fig. 11에 포함하였다. 이 히스토그램을 통해 S₄지반 분류 조건의 암반심도의 경계를 벗어나는 표본은 다른 지반으로 재분류되는 것을 확인할 수 있다.

이러한 과정을 통해 산정된 얕은 심도의 지반모델에 지각까지 지반층을 확장하기 위해서 깊은 심도에 KLL21S4에서 적용한 지각모델을 사용한다. 고주파수 대역의 증폭은 상부 수 미터(m) 내의 지반의 동적 특성에 큰 영항을 받으므로 KLL21S4과 함께 추가로 HPP를 적용하여 변동성을 고려한 국내 지반분류 S₄에 해당하는 토사지반 모델을 생성하였다. Fig. 12에서는 본 연구에서 설정한 일반 토사지반으로 구성한 모델의 전단파속도 주상도를 심도 10km까지 지각모델을 포함하여 나타내고 있으며 모델마다 공학적 암반의 출현 심도가 진한 가로 막대로 표시되어 있다.

Fig. 12

S₄ model using Homogeneous Poisson Processes including crustal velocity profile. Crustal velocity is derived using the similar fashion in KLL21S4 model

3.4 재해도에 상응하는 지반변위

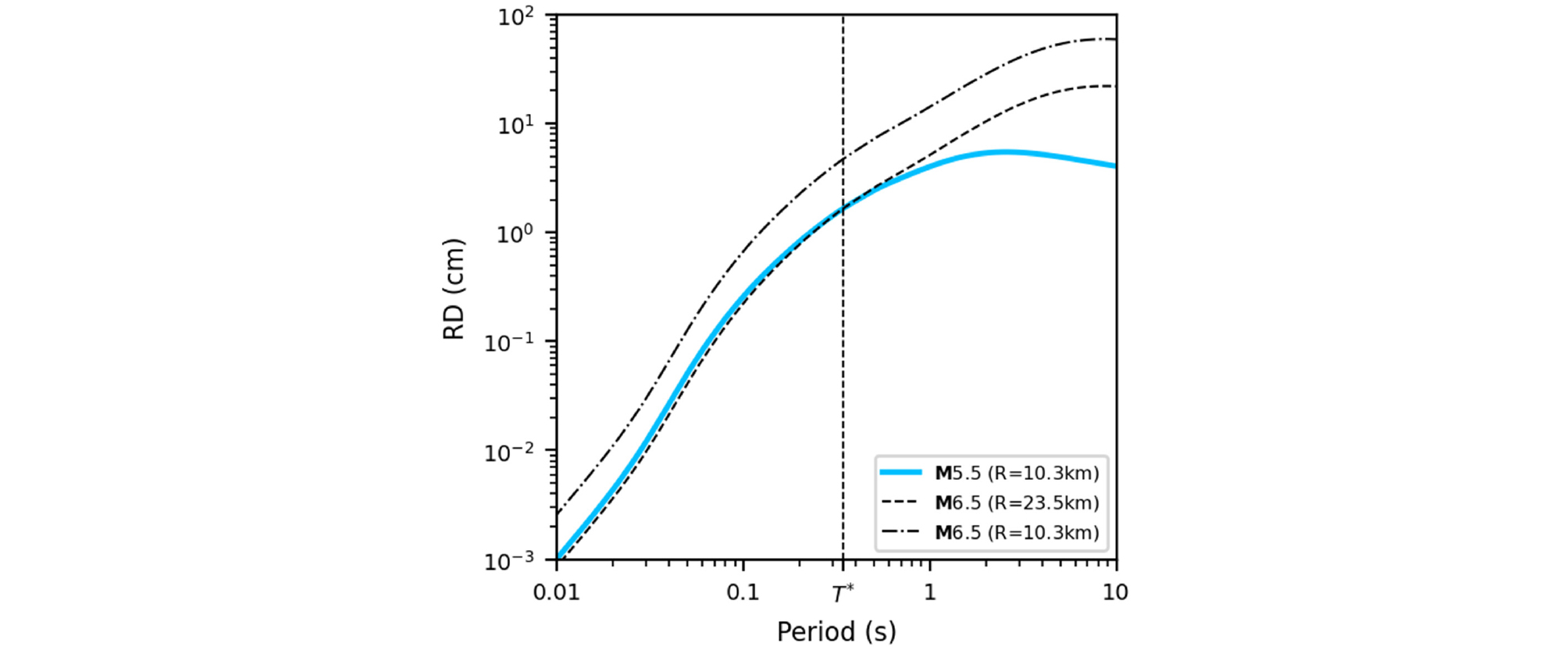
Fig. 13에서는 시나리오 지진과 비교하기 위해 동일한 설계스펙트럼 값을 갖는 규모 6.5 지진(거리 23.5km)과 함께 동일 단층면 거리를 갖는 규모 6.5 지진을 보여준다. 지반주기에 대해 동일한 설계스펙트럼 값을 갖는 지진의 경우, 대상 지반을 포함하여 일반적으로 지반주기(T_s) 0.5초 이하인 지반에서 변위의 차이는 매우 적은 것을 확인할 수 있으며, 0.5초 이상의 주기를 가진 지반에 대해서는 규모에 따른 지반변위에서 유의미한 차이가 나타나는 것을 확인할 수 있다.

Fig. 13

Displacement spectra of scenario earthquakes using stochastic method at KLL21S4 model site. M 6.5 earthquake with rupture distance of 10.3 km is plotted for comparison purpose

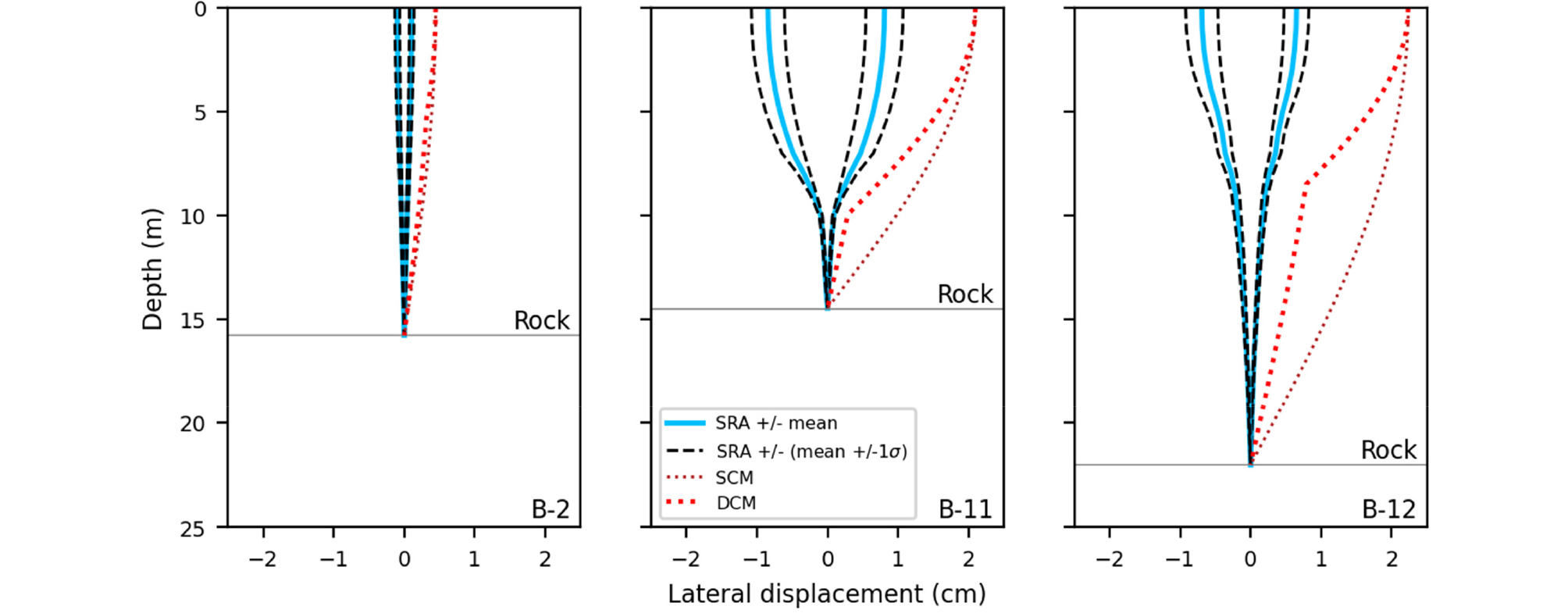
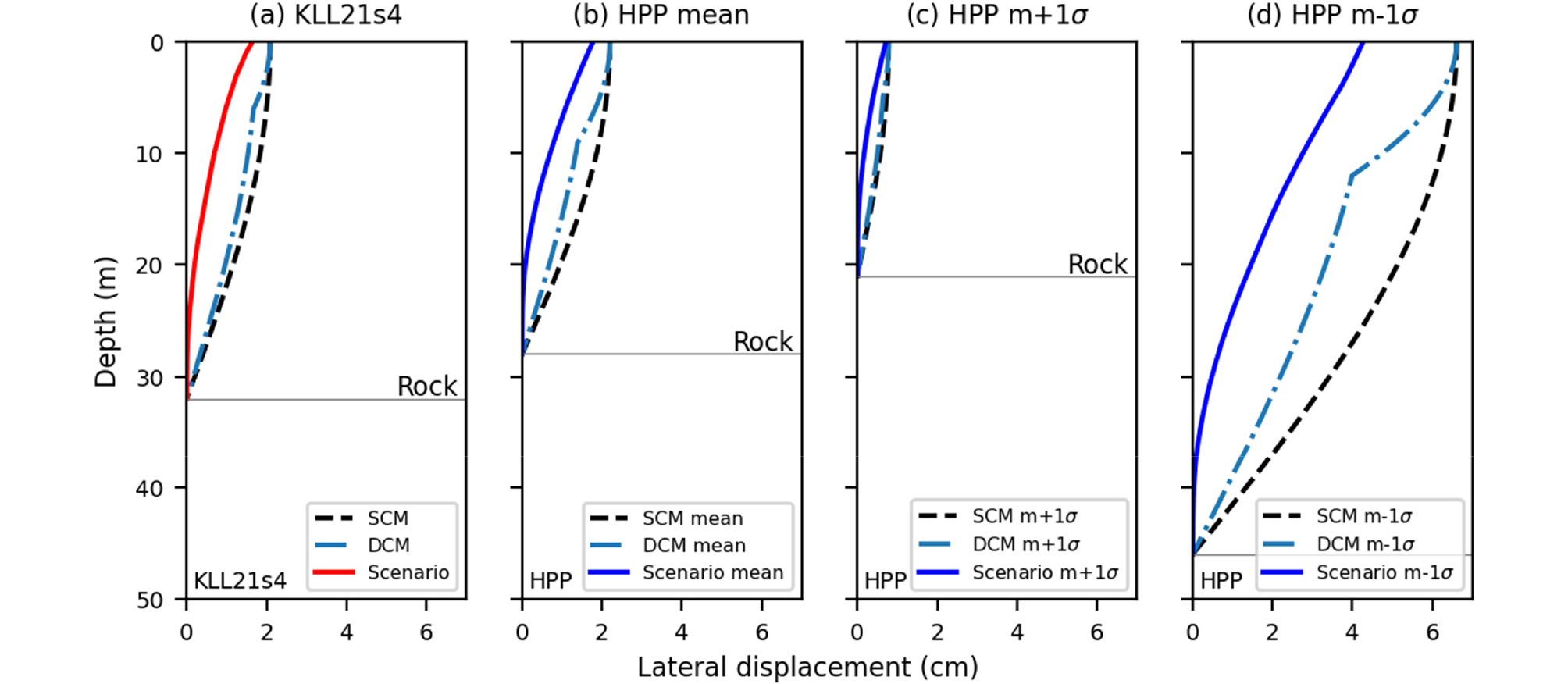
결과적으로 일반화 S₄ 토사지반모델(KLL21S4 모델)과 HPP를 사용하여 구성한 지반모델에 대하여 동일한 시나리오 지진원(규모 5.5, 거리 10.3km)에 대해 공학적 암반에서부터 지표면까지 심도 1m 간격으로 지반변위를 계산한 결과는 Fig. 14와 같다. 앞서 지반응답에서 확인한 바와 같이 국내 설계 지반가속도의 범위에 대해 과도한 감쇠비의 적용은 배제하였다. Fig. 14는 제안한 재해도 기반의 지반변위를 단순화 가정법(코사인법)과 비교하고 있는데, 지표면에서의 지반변위를 기준으로 KLL21S4 모델의 경우 1.64cm로 코사인법에 의한 지반변위의 약 79% 정도로 예측되었으며(Fig. 14(a)), 평균주상도에 대한 HPP 토사지반 모델의 경우 1.77cm로 코사인법의 약 81%로 산정되었다(Fig. 14(b)). KLL21S4 모델과 HPP모델은 다른 접근방법으로 구성된 지반모델임에도 불구하고 지반변위 산정 결과에서 유사한 결과를 보여준다. 분산을 고려한 HPP모델에서는 깊은 심도에서 공학적 암반이 출현하는 경우 4.26cm로 코사인법에 의한 지반변위 6.61cm의 약 65%로 산정되어 KLL21S4 모델이나 평균 HPP 지반의 경우보다 더욱 큰 차이가 나타났다(Fig. 14(d)). 기존의 단순화 가정법이 모든 지반모델에 대해서 과도한 변위를 산정하는 것에 반해, 본 연구에서 제안한 재해도 기반의 지반변위 산정 방법은 보다 합리적으로 변위를 예측하며 공학적 암반의 심도가 깊을수록 이러한 경향이 두드러졌다.

Fig. 14

Displacement of generic S₄ soil model (KLL21S4) and homogeneous Poisson Processes (HPP) sites when subjected to the hazard-consistent scenario earthquake simulation. The stochastic method is used to estimate relative lateral displacement

3.5 특정 지반에 대한 적용

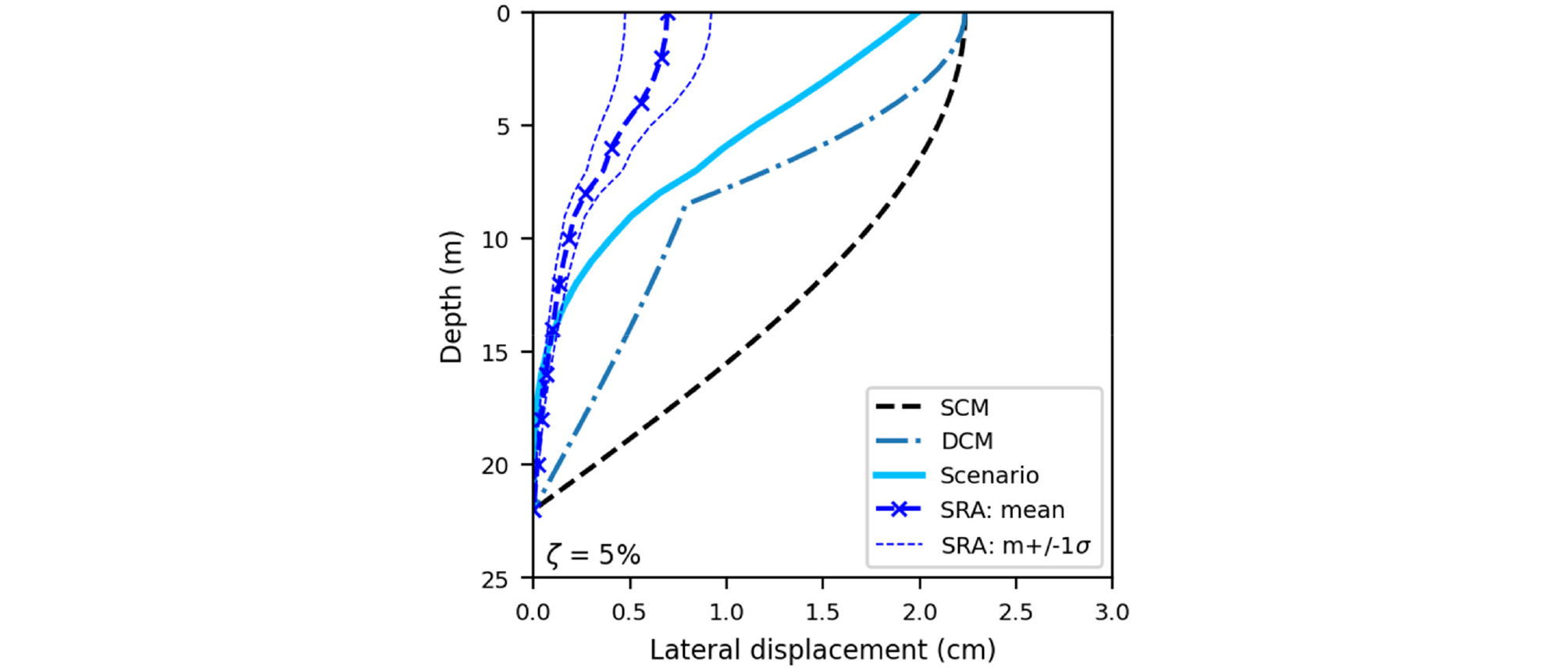
본 연구에서 제안한 국내 재해도 기반의 변위 산정을 통해 내진설계상 지반분류 같은 일반화된 지반에 대한 공학적 예측의 범위를 제공할 수 있지만, 실제 특정한 지반에 대한 지반변위 산정 또한 가능하다. 여기서는 앞서 살펴본 B-12 지점을 대상으로 본 연구에서 제안된 방법을 지반응답해석을 포함한 기존의 방법과 비교해본다. Fig. 15에서는 Fig. 6과는 달리 지반응답해석 결과에서 다른 방법과 비교가 쉽도록 1m 심도마다 변위의 절대값을 포락선으로 바꾸어 한 방향으로 표시하였다. 특정 지반을 대상으로 한 비교 결과 본 연구에서 제안하는 방법에 따른 예측이 기존의 두 방법, 즉 단순화 가정법과 지반응답해석의 결과 사이에 위치하는 것을 확인할 수 있다. 이 중, 지반응답해석과 제안 방법에 따라 도출한 지반변위 결과의 차이는 부지 증폭에 대한 해석 방법의 차이에 의해 발생한다. 즉, 제안 방법에서는 선형모델을 사용하고 있으나 지반응답해석은 등가선형모델로 비선형 특성을 반영하므로, 지표면에 가까워질수록 차이가 커지게 된다.

Fig. 15

Comparison of relative displacements at B-12 section

4. 결론 및 고찰

4.1 결론

국내 지중구조물의 지진하중으로서의 지반변위 산정에 흔히 적용되는 단순화 가정법(코사인법)은 견고한 암반 위에 한 층 또는 두 층의 균질한 토사지반으로 이상화한 지반모델의 변위를 심도에 따라 코사인 곡선의 호에 근사값으로 추정할 수 있다는 전제조건에서 출발한다. 이 단순화 가정법은 3개의 각기 다른 지반조건(S₂, S₃, S₄)에서 본 연구의 제안 방법에 비해 모두 보수적인 예측 결과를 도출하며, 지반응답 해석 결과와의 비교 시 그 차이는 4배 이상으로 과도한 평가를 하고 있다. 이러한 경향은 Park et al.(2010)의 기존 연구에서 확인된 것과 일치한다. 하지만 위의 공동구의 3개 지점에서는 지반응답해석이 단순화 가정법에 비해 큰 변위 결과를 나타내는 경우는 없었는데, 이는 대상 지반의 수가 적고, 비선형성이 큰 임의의 지반조건을 고려하지 않았기 때문이다. 코사인법을 사용한 지반변위 산정은 간편함 때문에 국내 지중구조물의 지진거동 평가에 흔히 적용되고 있으나, 실제 지중구조물이 설치되는 대상 부지의 다양한 지반층에 대한 조건을 충분히 반영할 수 없는 한계를 가지고 있다. 결론적으로 기존의 지반변위 산정에 있어서 살펴본 기존의 단순화 가정법은 지반변위를 산정하기에 적합하지 않으며 과도하게 보수적인 결과를 가져올 수 있다.

이에 비해 본 연구에서 제안한 방법은 국내 지진환경에 부합하는 지진원 스펙트럼을 사용하여 대상 부지 지반증폭 및 감쇠효과를 포함한 시나리오 지진을 통한 지반변위를 예측한다. 이때, 추계학적 강진동 모사를 통해 구현한 지진원 스펙트럼을 국내 지반환경을 고려한 일반화 지반 모델에 적용한다. 이러한 과정을 통해 부지효과가 반영된 지반 변위를 도출할 수 있다. 이 방법은 변동성을 고려한 일반화된 지반모델의 변위 상·하한값의 범위 예측(bounding analysis)이 가능하다는 장점이 있다. 예를 들어, 내진설계기준에 따른 지반분류 중 일반화 토사지반인 S₄에 대해서 지표 또는 공동구의 특정 심도에서의 지반변위 예측 범위를 사전에 기대할 수 있으며, 이는 특정부지에서의 지중구조물의 내진설계 및 평가에 매우 효과적으로 적용될 수 있을 것이다.

또한, 본 연구가 제시하는 재해도에 상응하는 지반변위 산정 방법은 단순화 가정법과 같이 과도하게 보수적인 결과를 도출하지 않는다. 이 방법은 다양한 지반층에 대해 고려하므로 합리적인 결과를 도출할 수 있다.

지진재해도에 상응하는 지반변위 산정방법은 앞서 언급한 일부 제약사항에도 불구하고 현재 지반응답해석에 기반한 방법이 가지는 문제점에서 보다 자유롭다. 또한, 선형 통로형 지중구조물의 지진해석의 경우 주로 횡단면에 대한 전단변형만을 검토하는 것에 비해, 본 연구에서 제안하는 방법은 지진파의 입사각을 고려하여 공동구의 주축 방향의 거동 평가에 적용하기가 쉽다는 장점이 있다. 이러한 이유는 대상부지의 지반 증폭 및 감쇠 효과를 고려할 때 Ray 이론(Wiggins, 1964)에 기반한 입사각의 고려가 매우 용이하기 때문이다. 결론적으로 본 연구에서 제시하는 방법은 근본적으로는 지반 단순화 가정과 같이 선형 지반응답해석의 한 방법이지만, 코사인법과 같이 지반층의 구성을 단일 층 또는 두 개 층으로만 제한하지 않으며 지진파의 전달경로에 있는 지각을 포함한 얕은 심도의 지반층을 모두 포함하고 여러 지반층에 대한 지반 증폭을 매우 신속하게 계산할 수 있다. 또한, 공학 실무에 있어서 다양한 변수를 고려한 비선형 모델을 사용하는 지반응답해석에 비해 지진파 저항(impedence)만을 변수로 사용하고 있으므로 상대적으로 간편하여 활용가능성이 높다. 동시에 국내 지진재해도에 상응하는 지반변위의 산정 시 국내 지반분류에 따른 지반변위의 다양한 주상도를 고려할 수 있으며 기존의 응답변위법에 대한 비교 지표로도 사용할 수 있다. 추후 S₄ 외의 다른 종류의 지반에 대해서도 일반화 지반모델을 구축하여 이 방법을 적용한다면, 평가지침에 지반분류와 심도별 지반변위의 상·하한값을 설정할 수 있으며 과도한 예측을 피할 수 있다.

4.2 일반적 지반응답 산정 관련 고찰

본 연구에서 기존의 응답변위법에 대해 몇 가지 부수적으로 발견한 점이 있다. 첫째로, 단순화 가정법 중 이중 코사인법에서 지반층 구분에 모호함이 있다. 국내기준(KISTEC, 2020)에 따른 이중코사인법의 적용에 있어서 지반층 구분에 대한 기준이 명확하지 않다. 실제 지반 대부분은 단일 층으로 이상화하기에 어려우며, 이중코사인법과 같이 2개 층으로 구분하더라도 다양한 층으로 구성된 대상 지반을 2개로 구분하는 위치, 즉 상층부의 변위가 합산되는 경계 심도의 결정에 따라 지반변위가 급격하게 달라진다. 앞에서 살펴본 B-2 지점과 달리 여러 층으로 뚜렷하게 구분되는 지층으로 구성된 B-12 지점의 경우 이중코사인법 적용 시 대표 지반층의 구분 심도에 따라 예측 결과의 차이가 발생하게 된다. 본 연구에서는 지반층 구분에 따른 각 층별 slowness(1/V_s)에 대한 편차를 비교하였으며, 지반층 구분은 일반적으로 이중코사인법에서 사용하는 토질 종류에 따른 경계와 함께 동일 토질층 내에서도 slowness의 기울기가 급격히 변하는 심도를 추가하였다(Fig. 16). 모든 경우에 대해서 지표면에서의 변위는 고정되어 있지만 공동구 심도에서의 변위는 지반층 구분에 따라 각기 다른 결과를 가져온다. 본 연구에서는 구분된 지반층 두께 가중치를 고려한 slowness 편차의 합이 최소가 되는 심도를 기준으로 구분하였다.

Fig. 16

The varied ground displacement results in Double Cosine Method; The different displacement estimation happens at B-12 location based on the averaging slowness profiles. The smallest deviation profile is selected for DCM

둘째로, 공동구 내진평가 지침에서는 붕괴방지 수준에 대한 검토에서 가정하고 있는 감쇠비가 20%이지만, 이는 과대평가된 감쇠비로 판단된다. 현행 공동구 내진평가 지침에서 이러한 수준의 감쇠비 적용 이유에 대해 설명하고 있지 않지만 터널 내진평가 지침(KISTEC, 2011)을 살펴보면 지중구조물의 경우 지표상의 콘크리트 구조물에 대한 감쇠비와 다른 특성을 보인다는 점을 들어 감쇠비의 보정(붕괴방지 수준에 대해 20%)을 설명하고 있다. 일반적으로 균열 콘크리트에 대해 3∼5%의 감쇠비를 적용하고, 이는 기존 연구와 해외 기준에서도 제안하는 범위이다(Newmark and Hall, 1982; CEN, 2004). 지상구조물의 외관에서 보이는 각종 부착물 등도 존재하지 않는 공동구와 같은 구조물이 기준의 설명과 같이 고유감쇠비를 가지기는 매우 어려우며 특히 국내의 설계지진수준(붕괴방지수준에 대한 유효지반가속도 0.154g)을 고려하면 더욱 과대평가된 감쇠비를 사용하고 있다.

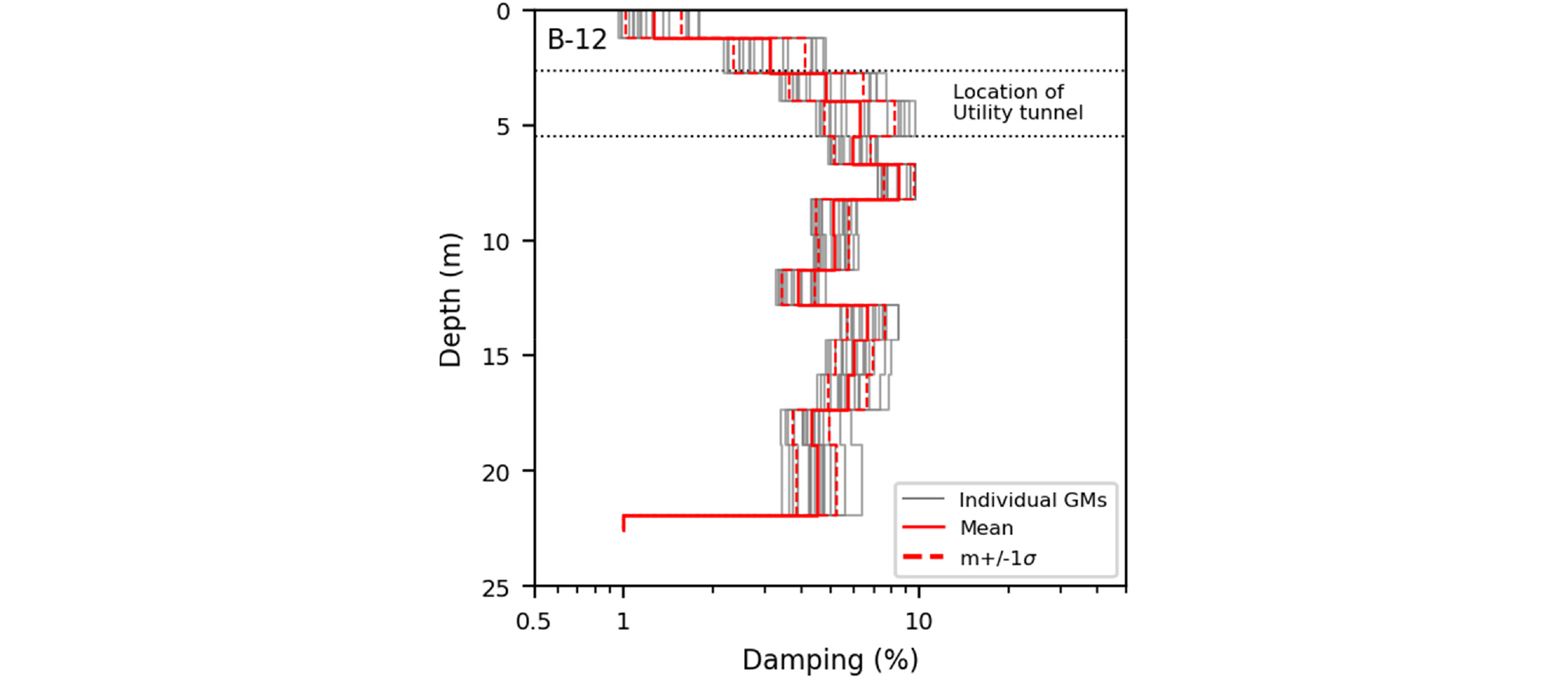
본 연구에서 지반응답해석을 통해 살펴본 지반층별 감쇠비의 최대값은 지표면의 변위가 가장 큰 B-12 지점의 공동구 심도 부근에서 19개 지반운동에 대해 평균 8% 가량으로 나타났으며 전체 지반층에 대해서 층 두께 가중치를 고려한 평균값은 약 5%이다(Fig. 17). 다른 두 단면에 대해서는 감쇠비의 평균값은 모두 5% 이하로 계산되었다. 따라서 단순화 가정에 기초한 코사인법의 경우 국내의 설계지진에 상응하는 지반가속도에 대해서 붕괴방지 성능수준의 검토에서도 5%의 감쇠비가 적합하다고 판단된다. Fig. 15에서는 이러한 방식으로 도출한 합리적인 감쇠비에 기초하여 단순화 가정법에 따른 지반변위와 재해도에 부합하는 지반변위를 산정하였다.

Fig. 17

Damping profile at B-12 section using 1-D site response analysis. The weighted average damping for whole soil layers is 5%