Frost Heave of Frost Susceptible Soil According to Performance of Thermo-syphon

Dong-Su Park; Mun-Beom Shin; Young-Kyo Seo

doi:10.7843/kgs.2021.37.10.27

Preview

Journal of the Korean Geotechnical Society. 31 October 2021. 27-40
https://doi.org/10.7843/kgs.2021.37.10.27

Frost Heave of Frost Susceptible Soil According to Performance of Thermo-syphon

열 사이펀 성능에 따른 동상민감성 지반의 거동 비교

Dong-Su Park¹

Mun-Beom Shin²

Young-Kyo Seo³^*

박 동수¹

신 문범²

서 영교³^*

¹Member, Graduate Student, Dept. of Convergence Study on the Ocean Science and Technology, Korea Maritime and Ocean Univ.

²Member, Graduate Student, Dept. of Convergence Study on the Ocean Science and Technology, Korea Maritime and Ocean Univ.

³Member, Prof., Dept. of Ocean Engrg., Korea Maritime and Ocean Univ. & Adjunct Prof., Dept. of Convergence Study on the Ocean Science and Technology, Korea Maritime and Ocean Univ.

¹정회원, 한국해양대학교 해양과학기술융합학과 박사과정

²정회원, 한국해양대학교 해양과학기술융합학과 박사과정

³정회원, 한국해양대학교 해양공학과 교수 및 해양과학기술융합학과 겸임교수

^{*Corresponding Author}

ABSTRACT

The construction method to prevent the frost heave or thaw settlement is called the ground stabilization method, and the thermo-syphon is one of the typical ground stabilization methods. The thermo-syphon has recently been developed with a simple analysis model and thermal analysis has been carried out, but the frost heave of frost susceptible soil was not considered. This study was conducted using ABAQUS internal user subroutine to develop the numerical analysis model (Coupled thermo-mechanical) that can simultaneously perform thermal analysis for the temperature change of the soil according to the thermo-syphon and structural analysis to predict the frost heave of the soil accordingly. As a result of the numerical analysis, the frost heave of the soil decreased as the performance of the thermo-syphon increased. As for the main results, when the thermo-syphon which has contain 25%, 50%, and 100% of refrigerant filling ratio was applied, the reduction ratio of the frost heave was 5.5%, 14.4%, and 21% respectively.

Keywords

Coupled thermo-mechanical model

Frost heave

Frost susceptible soil

Porosity rate function

Thermo-syphon

동상민감성 지반의 융기 및 침하 방지를 위한 공법을 지반 안정화 공법이라고 하며 열 사이펀은 대표적인 지반 안정화 공법 중 하나이다. 열 사이펀은 최근 간편한 해석모델 개발과 더불어 열 해석이 진행되었지만, 이에 따른 동상민감성 지반의 열적 거동을 고려하지 않았다. 따라서 본 연구는 열 사이펀의 성능에 따른 지반의 온도 변화를 위한 열 해석과 이에 따른 지반의 거동을 예측하기 위한 구조해석을 동시에 수행하기 위해 ABAQUS 내부 사용자 서브루틴을 사용하여 열 사이펀을 적용한 TM(Thermo-Mechanical) 모델을 개발하여 열 사이펀의 성능에 따른 지반 융기 억제성능을 확인하였다. 해석결과 열 사이펀의 성능 증가에 따라 지반의 최종 융기가 감소하였으며 냉매 충전율 25%, 50% 그리고 100%의 열 사이펀 적용 시 각각 5.5%, 14.4%, 21% 융기 억제성능을 나타내었다.

MAIN

1. 서 론
2. 동상민감성 지반 거동 모델 및 열 사이펀 모델
2.1 동상민감성 지반
2.2 동상민감성 지반의 부동수분 경향
2.3 Porosity rate function 모델
2.4 열 사이펀 모델
3. 수치해석 모델 내부 기본 방정식
3.1 TM 모델 내부 사용자 서브루틴 구성
3.2 열 물성 변화 및 에너지 평형
3.3 지반 동결에 의한 체적 팽창
4. 수치해석 방법 및 결과
4.1 동결 융기 모델 검토
4.2 수치해석 모델링 및 케이스
4.3 수치해석 결과 및 검토
5. 결 론

1. 서 론

극한지 지반의 경우 외기 온도 혹은 지반구조물(Ground structure) 자체 온도에 의해 지반의 동결 융기(Frost heave) 및 침하(Thaw settlement)현상이 발생한다. 이러한 융기 및 침하 현상에 취약한 지반을 동상민감성 지반(Frost susceptible soil)이라 하며 해당 지반의 동결 거동은 지반 구조물에 따라 영구동토(Permafrost area) 뿐만 아니라 계절성 동토지역(Seasonal frost area)에서도 고려해야할 사안이다. 극한지 지반의 동결 융기 및 침하는 수송배관의 좌굴, 포장 도로 지역의 침식 등 설치된 구조물의 구조적 안정성 문제를 야기한다(Li et al., 2019; Park et al., 2021). 따라서 동상민감성 지반의 동결 및 융해 특성에 관한 연구, 그리고 지반 동상에 의한 구조물의 파괴를 예방하기 위한 지반 안정화 공법들이 연구되어왔다. 먼저 동상민감성 지반의 동결 및 융해특성에 관한 연구는 실험적 연구부터 수치해석 모델 연구까지 다양하게 존재한다. 지반의 동결특성의 경우 온도에 따른 간극 내부 수분의 동결 및 지속적인 간극수의 이동으로 인한 얼음 띠(Ice lens) 형성과 같은 복잡한 열-수리 역학적 메커니즘이 결합되어있어 각각의 연구가 진행되어 왔다. 온도에 따른 지반 간극 내부의 수분 변화 및 잔류 부동수분에 대한 실험적 연구는 Anderson and Tice(1972)가 실험 데이터를 기반으로 지수 형태의 경향곡선을 제안한 연구가 대표적이며, Michalowski(1993)은 수치해석에서의 수렴성을 높이기 위해 Anderson and Tice(1972)의 경향곡선을 수정한 경향곡선 식을 제시하였다. 동상민감성 지반의 동결 융기특성의 연구 중 실내 실험의 경우 Fukuda et al.(1997) 연구가 대표적으로 지반 시료의 상, 하부 온도 구배에 따른 지반의 동결 융기 경향을 산정하였다. 지반의 동결 융기 산정을 위한 모델연구의 경우 Empirical and Semi-empirical 기반의 SP(Segregation Potential) 모델(Konrad and Morgenstern, 1980), Hydrodynamic 기반의 Frost 모델(Guymon et al., 1993), Rigid Ice 타입의 PC-Heave 모델(O’Neill and Miller, 1982), Thermo-mechanical 타입의 모델(Hartikainen and Mikkola, 1997; Michalowski, 1993; Michalowski and Zhu, 2006) 등 다양한 모델들이 제안되어왔다. 다음으로 지반 안정화 공법에 대한 연구도 동시에 진행되어왔다. 여기서 지반 안정화 공법이란 동상방지재의 사용, 굴착 및 되메움재 사용, VSM(Vertical support member) 설치 그리고 열 사이펀(Thermo-syphon) 적용 등을 예로 들 수 있으며(Park et al., 2021) 대표적인 지반 안정화 공법 중하나인 열 사이펀은 열 사이펀 내부의 냉매가 지중의 열을 흡수하여 기체 상태로 증발, 차가운 외기온도로 인해 다시 액체로 응축되는 메커니즘을 가지며 지중과 대기의 온도차로 작동하는 구조체이다(Andersland and Ladanyi, 2004). 열 사이펀은 내부 냉매의 2상 유동(Two-phase flow)에 의한 열 교환 원리로 작동되며 이를 전산유체역학(CFD)을 통한 수치해석, 열원의 경계조건으로 간소화한 연구들이 진행되어 왔다. 하지만 전산유체역학을 통한 연구(Alizadehdakhel et al., 2010; Fadhl et al., 2013; Jafari et al., 2017)들은 그 자체로도 이상 유동의 복잡한 계산을 동반하므로 방대한 수치해석 시간이 요구되며 열 사이펀과 지반의 상호작용에 의한 지반의 거동해석은 보다 막대한 수치해석 시간이 요구된다. 따라서 열 사이펀 적용에 따른 지반의 동결 및 침하 거동 해석의 경우 열 사이펀을 유체해석을 통해 모사하는 방법이 아닌 열 사이펀을 하나의 열원으로 간소화 한 연구들이 진행되어왔다(Park et al., 2021). 대표적으로 Xu et al.(2011), Abdalla et al.(2015), Abdalla et al.(2016)의 연구는 상용수치해석 프로그램인 ABAQUS내부 사용자 서브루틴인 USDFLD를 사용해 열 사이펀 내부의 열 유속(heat flux)의 방향에 따라 열전도율을 부여하는 방식으로 구현하였다. 하지만 해당 연구의 열 사이펀 적용의 경우 임의의 열전도율을 부여하여 사용하였으며 해당 물성치 및 열 사이펀을 통한 지반의 온도변화 및 거동에 대한 검증은 이루어지지 않았다. 다음으로 열 사이펀의 열전달 성능은 해당 열 사이펀에 대해 단위길이, 단위 면적당 전도도로 표시하며(Jang et al., 2014), 이러한 열 사이펀의 열전달 성능을 산정하기 위해 Jang et al.(2014), Lee et al.(2014)은 상용 수치해석 프로그램인 Temp/w 내부 열 사이펀 열 해석을 통한 지반의 온도 경향과 실내실험을 통해 도출한 지반의 온도경향를 비교하여 해당 열 사이펀의 성능을 도출하였다. 하지만 해당 연구들은 지반의 거동은 고려하지 않았다. 최근 지반의 동결 융기 및 침하 해석을 수행 할 수 있는 FEM 프로그램 툴인 ABAQUS를 통한 열 사이펀 모델개발연구가 진행되어(Park et al., 2021) 기존 실내모형실험(Jang et al., 2014; Lee et al., 2014)연구 결과와 열 사이펀 모델의 수치해석 결과의 검증 연구가 진행되었다. 하지만 기존 실내모형실험은 동결 융기의 정도가 미미한 사질토로 수행되었기에 지반의 동결 융기 및 침하에 대한 지반 거동 해석은 이루어지지 않았다. 따라서 본 연구는 기존 열 사이펀 모델(Park et al., 2021)에 따른 열역학적 해석 및 이에 따른 지반의 동결 융기 및 침하에 대한 거동해석을 동시에 수행 할 수 있는 TM(Thermo-Mechanical) 모델을 ABAQUS 내부 사용자 서브루틴을 이용하여 사용 하였으며 기존 모형실험으로 도출된 열 사이펀의 성능을 바탕으로 동상민감성 지반의 동결 융기 억제 성능을 비교 분석하였다.

2. 동상민감성 지반 거동 모델 및 열 사이펀 모델

2.1 동상민감성 지반

지반의 동상이란 지반 내부의 온도가 하강하여 지반 내 간극의 간극수의 동결 및 지속적인 간극수 공급에 의한 지반의 팽창현상을 뜻한다(Taber, 1930). 이러한 지반의 동결 팽창은 원 지반 단위 체적의 9% 이상으로 지반의 체적변화가 발생하며, 이러한 체적변화에 따른 팽창력은 지반 구조물의 일부분을 들어 올릴 정도의 큰 힘을 갖는다(Terzaghi, 1952). 지반의 동결 시 지반 내부에 생성되는 얼음의 경우 Fig. 1과 같이 두 가지 형태로 분류 할 수 있으며, 부피변화에 큰 영향을 미치지 않는 공극빙(Pore ice), 그리고 부피변화에 큰 영향을 미치는 얼음 띠(Ice lens)로 구분 할 수 있다. 여기서 부피 팽창의 중요한 요인인 얼음 띠 형성이 잘 이루어지는 지반을 동상민감성 지반이라고 한다. 이러한 동상민감성 지반의 경우 실트, 점토질 흙으로 구성되어 있으며 이러한 흙은 간극이 작고 모세관 현상이 잘 형성되는 지반이다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F1.jpg

Fig. 1

Characteristic of Freezing soil (Zhang, 2014; Lay, 2005)

2.2 동상민감성 지반의 부동수분 경향

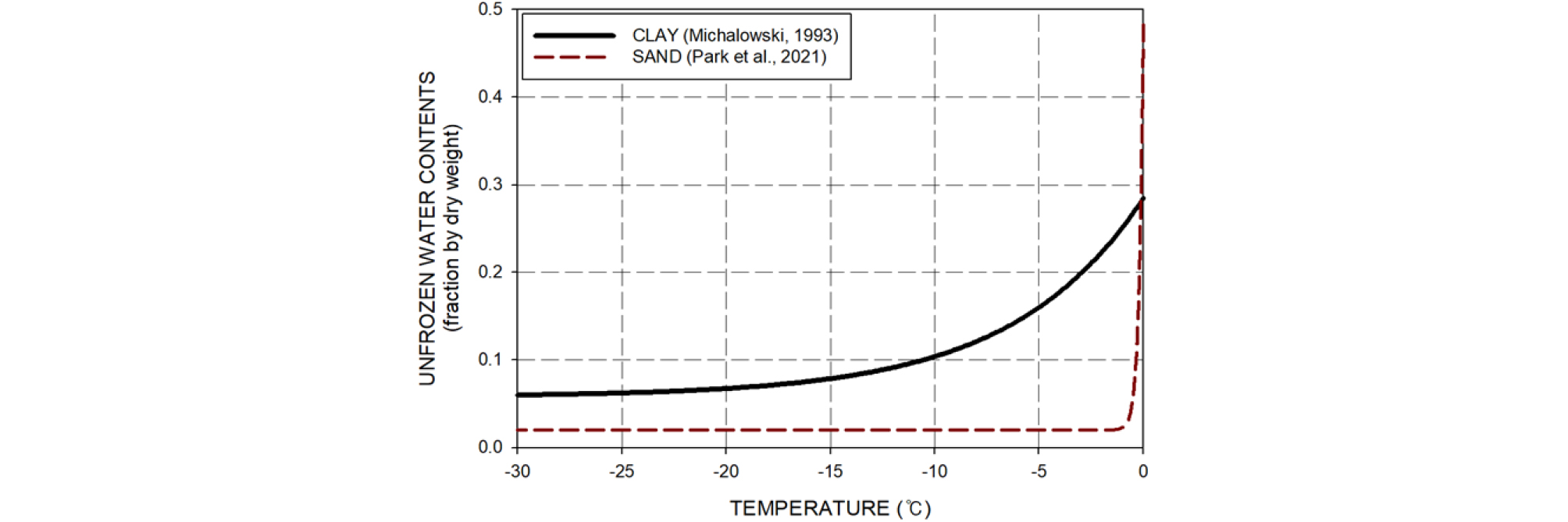
동상민감성 지반의 동결은 지반 간극 내 간극수의 동결 그리고 지속적인 수분 공급에 의한 얼음 띠 형성을 동반한다. 여기서 간극 내부 간극수의 경우 그 전체가 공극빙으로 형성되지 않고 일부가 동결되지 않은 간극수로 남아있는데 이를 부동수분이라 한다. 이러한 부동수분의 경우 지반의 종류에 따라 최종 잔류 부동수분 및 온도에 따른 부동수분 감소 경향이 다르다. 자갈, 모래와 같은 지반의 경우 온도가 동결시점(Freezing point of water)을 기점으로 급격하게 하강하는 경향을 보이며 점토 혹은 실트와 같은 지반은 이보다 완만하게 부동수분이 감소하는 경향을 보인다. 부동수분 감소 경향은 과거 실험 연구를 통해 데이터가 적립되어왔으며, Tice et al.(1976)은 실험 데이터를 통해 지수형태의 경향곡선을 제시하였다. 해당 경향곡선은 Eq. (?)과 같으며 ‘α’, ‘β’는 각 지반특성에 따른 곡선 경향계수, 그리고 ‘θ’는 온도를 뜻한다.

(1)

w_{u} = α θ^{β}

하지만 해당 경향식의 경우 동결시점 온도에서 무한한 값을 가지는 식으로 수치해석에서의 수렴성 문제가 존재한다. 따라서 Michalowski(1993)은 이를 보완한 경향식을 제시하였으며 Eq. (2)와 같다. 여기서 ‘w^*’는 아주 낮은 온도에서의 수렴된 잔류 부동수분량, ‘ $w$ ’는 동결 이전 간극수분량, ‘α’는 지반 특성에 따른 곡선 경향계수, 그리고 ‘T₀’는 동결시점 온도(0℃)를 뜻한다.

(2)

w_{u} = w^{*} + (\bar{w} - w^{*}) e^{α (T - T_{0})} T < T_{0}, \frac{\partial T}{\partial t} < 0

본 연구에서는 Michalowski의 부동수분 경향식을 사용하였으며 해당 경향식을 사용한 Clay 지반의 부동수분 경향은 Fig. 2에 도시하였다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F2.jpg

Fig. 2

Unfrozen water contents (Michalowski, 1993; Park et al., 2021)

2.3 Porosity rate function 모델

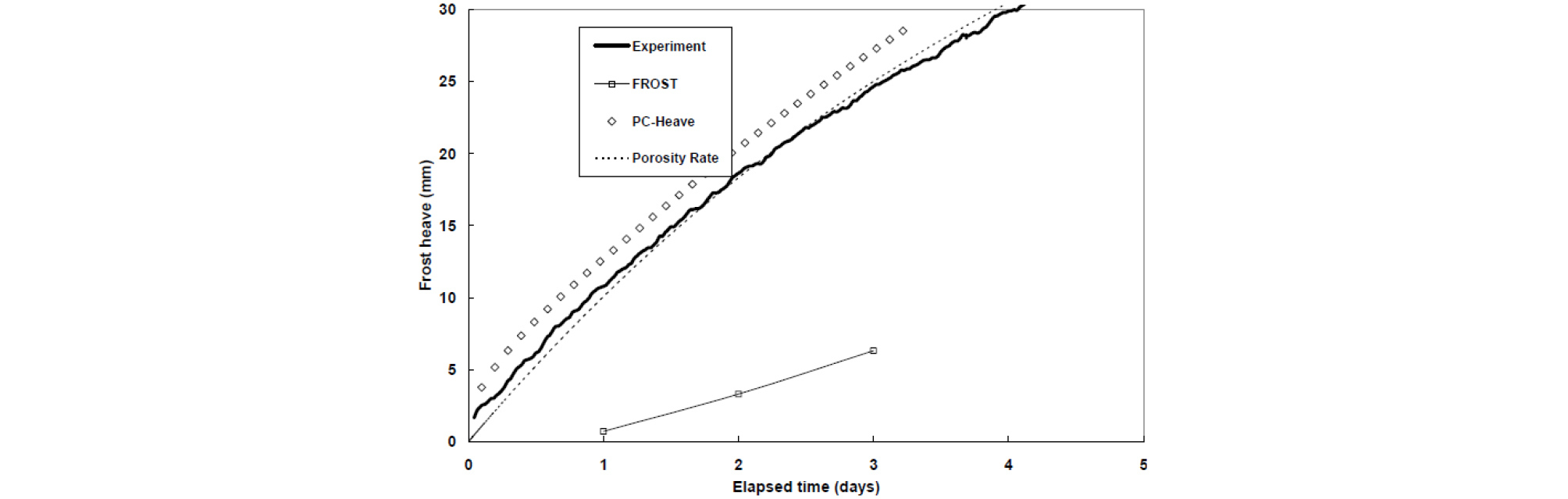
본 연구에서 사용한 동상민감성 지반의 동결 융기 모델은 Michalowski(1993)이 제안한 모델의 수정버전인 Zhang and Michalowski(2015)의 Porosity rate function 모델을 사용하였다. 해당 동결 융기 모델 및 다른 모델의 비교는 Fig. 3과 같으며 실내 모형실험결과와 잘 부합하는 동결 융기 경향을 보인다(Henry et al., 2005).

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F3.jpg

Fig. 3

Frost heave results between heave model and experiment (Henry et al., 2005)

Porosity rate function은 대표적인 Thermo-mechanical(TM) 타입의 동결 융기모델로서 해당 모델의 특징은 다음과 같다. 먼저 지반은 완전 포화된 지반으로 체적은 흙, 간극수 및 얼음 3상으로 구성된다. 해당 구성 중 간극수, 얼음의 경우 온도 의존적으로 변화하며 3상의 체적분율에 따라 밀도, 열전도율, 비열과 같은 물성이 정의된다. 이러한 3상 부피비율의 변화는 Eq. (3)과 같으며, 앞서 기술한 부동수분 경향곡선의 영향을 따른다. 여기서 ‘n’은 간극률, ‘θ’는 3상의 체적분율, ‘ρ’는 밀도를 뜻하며 위첨자 ‘s’, ‘w’, ‘i’는 각각 흙입자, 간극수 및 얼음을 뜻한다.

(3)

θ^{(s)} = 1 - n θ^{(w)} = (1 - n) (\frac{ρ_{s}}{ρ_{w}}) w_{u} θ^{(i)} = n - θ^{(w)}

지반의 팽창은 모세관 현상에 의해 유입되는 간극수의 얼음 띠 형성을 통해 결정된다. TM 타입의 Porosity rate function은 이를 온도 변화에 따른 간극률의 변화율로 지반의 동결 팽창을 정의하였으며 해당 식은 Eq. (4)와 같다.

(4)

\dot{n} = \dot{n_{m}} {(\frac{T - T_{0}}{T_{m}})}^{2} \cdot e^{1 - {[\frac{T - T_{0}}{T_{m}}]}^{2}} \cdot \frac{|\frac{\partial T}{\partial l}|}{g^{T}} \cdot e^{- (\frac{|σ'_{k k}|}{ς})} \cdot e^{- \frac{θ^{(i)}}{θ^{(w)}}}

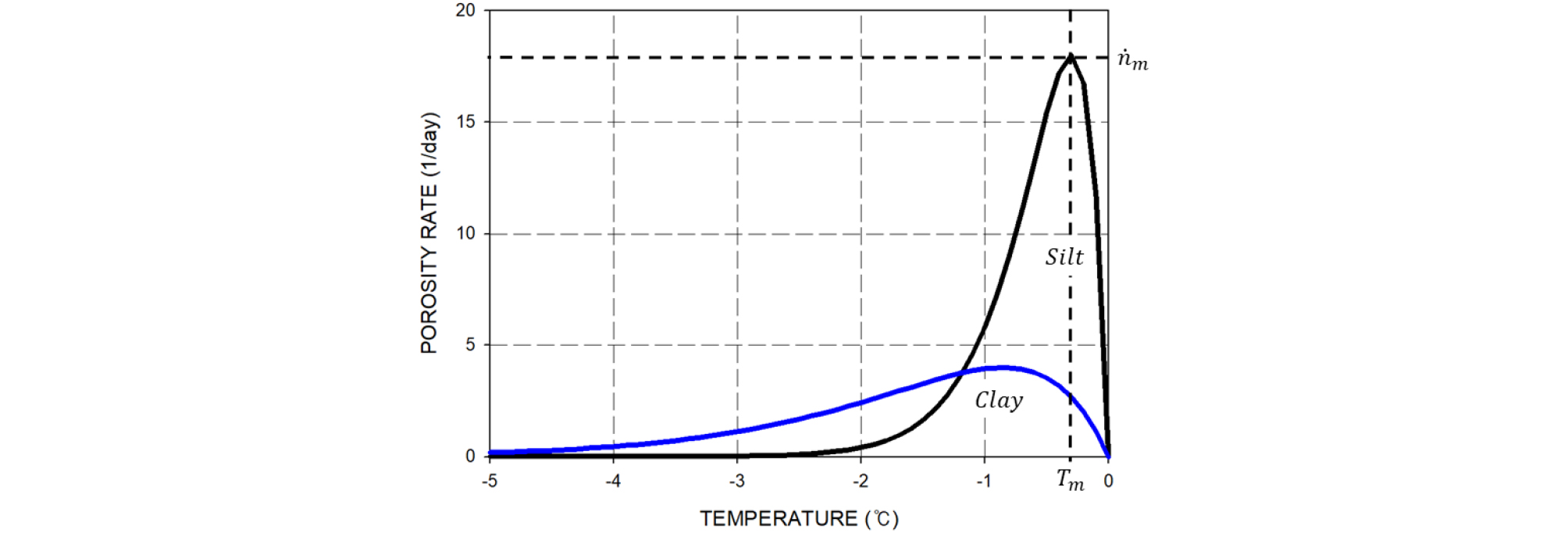
해당 식의 핵심 요소를 살펴보면 다음과 같다. ‘T’, ‘T₀’, ‘T_m’은 각각 현재 온도, 동결시점 온도, 간극률 변화율(Porosity rate)이 최대가 될 때의 온도를 의미하며, ‘ $\dot{n_{m}}$ ’은 ‘T_m’에서의 최대 간극률 변화율을 의미한다. ‘g_T’는 ‘T_m’에서의 온도구배를 뜻하며 ‘ $\frac{\dot{n_{m}}}{g_{T}}$ ’의 값은 흙에 따라 일정한 값을 가진다. ‘ $\frac{|\frac{\partial T}{\partial l}|}{g_{T}}$ ’항은 열의 흐름방향에서의 온도구배에 따른 간극률 변화율의 관계를 나타낸다. 또한 ‘ $e^{- (\frac{|\bar{σ}'_{k k}|}{ς})}$ ’항은 흙의 응력상태에 따른 간극률 변화율의 감소관계를 나타낸다. 여기서 ‘ $|\bar{σ}'_{k k}|$ ’은 1차 응력불변량 그리고 ‘ζ’는 특정한 흙에 대한 매개변수를 나타낸다. 식의 마지막 항 ‘ $e^{- \frac{θ^{(i)}}{θ^{(w)}}}$ ’은 간극률이 무한대로 증가하지 못하게 설정하는 항이다. 해당 식의 자세한 개념은 Zhang and Michalowski(2015)을 참고하면 알 수 있다. 해당 식을 통해 산정된 온도에 따른 간극률 변화율은 Fig. 4에 도시하였다(Michalowski and Zhu, 2006).

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F4.jpg

Fig. 4

Porosity rate by soil type (Michalowski and Zhu, 2006)

2.4 열 사이펀 모델

본 연구에서 사용한 열 사이펀 모델은 Park et al.(2021)의 열 사이펀 모델로 해당 모델은 열 사이펀을 별도로 모델링하지 않고 열 사이펀과 지반의 경계면의 경계조건으로 열 사이펀 증발부의 작용을 정의하는 방법이다. 해당 모델은 ABAQUS 프로그램 내부 사용자 서브루틴인 DFLUX를 사용하여 Eq. (5)와 같이 열 유속(q")을 정의하였다. 여기서 ‘Q_syphon’은 열 흐름율(Heat flow rate)을 나타내며, ‘A_syphon’은 열 사이펀과 지반의 경계면의 면적을 나타낸다.

(5)

q " = - \frac{Q_{s y p h o n}}{A_{s y p h o n}}

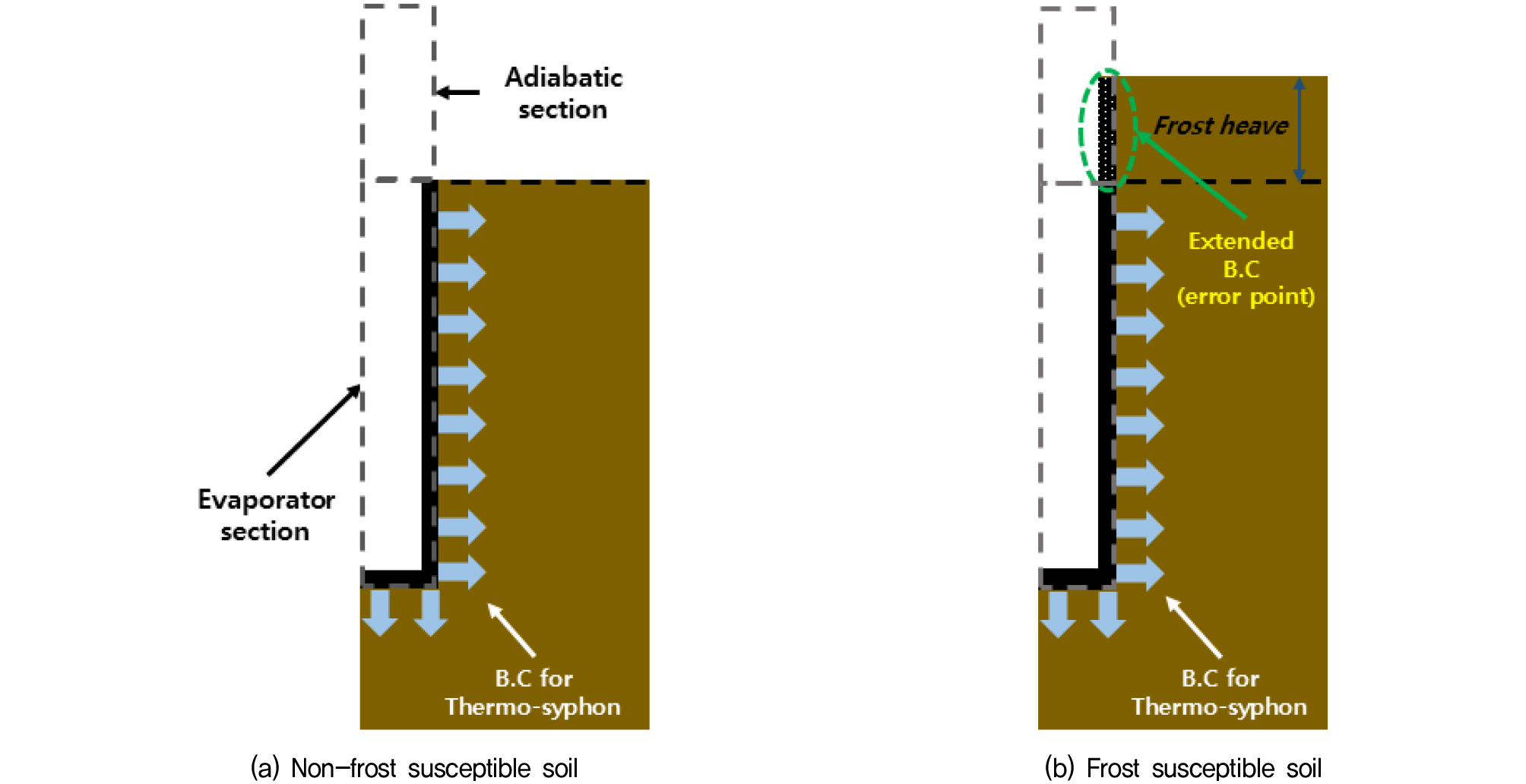
기존 열 사이펀 모델의 경우 동결 융기가 거의 없는 사질토로 수행한 연구이기에 Fig. 5(a)에서 나타낸 증발부(Evaporator section)와 흙의 경계면이 변하지 않았지만, 본 연구는 동상민감성 지반의 동결 융기로 인해 해당 모델을 그대로 적용하면 Fig. 5(b)와 같이 지반이 융기함에 따라 경계조건을 부여한 증발부가 동시에 증가하는 문제가 발생한다. 따라서 본 연구에서는 열 사이펀을 별도로 모델링 하여 기존 증발부에서만 열 유속을 정의 할 수 있게 변경하였으며, 증발부 이외 다른 섹션은 단열조건을 사용하여 별도의 열 교환이 일어나지 않게 적용하였다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F5.jpg

Fig. 5

Issue for thermo-syphon model (a) Non-frost susceptible soil (b) Frost susceptible soil

3. 수치해석 모델 내부 기본 방정식

3.1 TM 모델 내부 사용자 서브루틴 구성

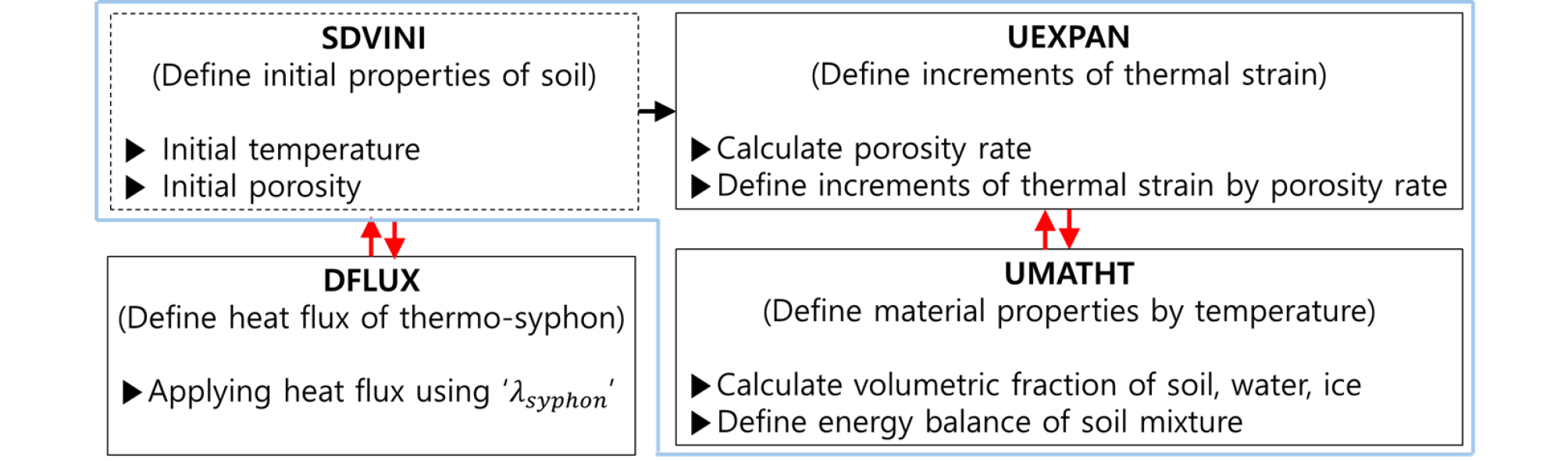
열 사이펀을 적용한 동상민감성 지반의 거동을 구현하기 위하여 본 연구에서는 Fig. 6과 같이 ABAQUS 내부 서브루틴을 사용하였다. 먼저 열 사이펀은 기존 연구(Park et al., 2021)와 같이 열 사이펀의 작동을 경계조건으로 부여하는 방식으로 서브루틴 DFLUX를 사용하였다. 하지만 기존 연구와는 달리 별도의 열 사이펀을 모델링하여 증발부를 지정, 해당 섹션만 경계조건을 부여하였으며, 그 외 섹션의 경우 단열조건을 부여하였다. 다음으로 지반의 열전도율, 비열, 밀도 및 얼음 생성에 따른 잠열효과는 서브루틴 UMATHT를 사용하여 정의하였다. 해당 서브루틴에서 정의되는 재료적 특성은 흙입자, 간극수 그리고 얼음의 3상 체적분율에 따라 결정되며, 해당 체적분율은 Eq. (2)의 온도에 따른 부동수분을 통해 정의하였다. 마지막으로 얼음 띠 형성에 의한 부피증가를 구현하기 위하여 서브루틴 UEXPAN을 사용하였으며 해당 서브루틴을 통해 Porosity rate function을 이용한 변형률 증분을 정의하였다. 서브루틴 DFLUX, UMATHT 그리고 UEXPAN은 시간 증분 끝에서 정의 되며 온도, 온도구배, 간극률, 얼음 띠의 체적분율 등 상태 변수(State variables)들은 각 시간 단계(Time step)에서 상호 영향을 받는다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F6.jpg

Fig. 6

User-subroutines for Thermo-mechanical coupling

3.2 열 물성 변화 및 에너지 평형

포화된 동상민감성 지반의 구성요소(흙입자, 간극수, 얼음)의 체적분율에 따른 열 물성 변화, 얼음 생성에 따른 잠열의 영향을 정의하기 위해 사용자 서브루틴 UMATHT을 사용하였다. 해당 서브루틴에서 사용된 기본 개념은 다음과 같다. Eq. (3)에서 정의된 흙, 간극수, 얼음의 3상 체적분율은 Eq. (6)과 같이 정의할 수 있다. Eq. (6)에서 정의된 각 성분의 체적분율(θ)은 간극률 ‘n’ 및 간극수율 ‘υ’으로 나타낼 수 있다. 여기서 ‘υ’는 Eq. (7)과 같이 정의된다(Michalowski, 1993). 아래 식들의 위 첨자의 경우 흙, 간극수, 얼음에 해당하며 각각 (s), (w), (i)로 표기하였다.

(6)

θ^{(s)} = \frac{V^{(s)}}{V} = 1 - n, θ^{(w)} = \frac{V^{(m)}}{V} = υ n, θ^{(i)} = \frac{V^{(i)}}{V} = υ (1 - n)

(7)

υ = \frac{V^{(w)}}{V^{(w)} + V^{(i)}}

다음으로 Eq. (6)에서 정의된 3상의 체적분율을 통해 밀도, 열전도율, 비열 등을 정의하였다. 밀도(ρ)는 Eq. (8)과 같으며, 비열(c)은 Eq. (9) 그리고 열전도율(λ)은 Eq. (10)와 같이 정의할 수 있다(Johansen, 1975; Johnston et al., 1981).

(8)

ρ = θ^{(s)} ρ^{(s)} + θ^{(w)} ρ^{(w)} + θ^{(i)} ρ^{(i)}

(9)

c = θ^{(s)} ρ^{(s)} c^{(s)} + θ^{(w)} ρ^{(w)} c^{(w)} + θ^{(i)} ρ^{(i)} c^{(i)}

(10)

\log λ = θ^{(s)} \log λ^{(s)} + θ^{(w)} \log λ^{(w)} + θ^{(i)} \log λ^{(i)}

마지막으로 잠열(L)의 경우 얼음의 체적분율 변화에 의해 발생되며 잠열 영향을 고려한 에너지 평형 방정식은 Eq. (11)와 같이 정의된다. 위 식들에서 정의된 물성치 및 에너지 증분은 서브루틴 UMATHT의 시간 증분 끝(End of time step)에 정의하였다.

(11)

c \frac{\partial T}{\partial t} - L \frac{\partial θ^{(i)}}{\partial t} - \nabla (λ \nabla T) = 0

3.3 지반 동결에 의한 체적 팽창

지반동결에 의한 체적 팽창은 본 연구에서는 서브루틴 UEXPAN을 사용하여 정의하였다. 총 변형률 증분은 Eq. (12)과 같이 탄성 변형률 증분, 소성 변형률 증분 및 열 변형률 증분의 합으로 나타낼 수 있다. 본 연구에서는 열 사이펀의 성능에 따른 지반의 동결에 대한 해석이며, 지반의 융해 혹은 지반 상부의 하중의 변화가 없는 해석이다. 따라서 해석 시간의 단축을 위해 소성변형을 고려하지 않고 기존 문헌(Ladanyi and Shen, 1993; Michalowski and Zhu, 2006)에서 사용된 온도에 따른 탄성계수를 부여하여 탄성변형 및 열 변형만 고려하였으며 해당 탄성계수는 Table 1에 나타내었다.

(12)

d ε_{i j} = d ε_{i j}^{e} + d ε_{i j}^{p} + d ε_{i j}^{t h}

Table 1.

Properties and parameters of frost susceptible soil for numerical analysis (Zhang and Michalowski, 2015)

Material properties of soil
Density [ ρ^(s), ρ^(w), ρ⁽ⁱ⁾ ]	2620, 1000, 917 (kg m^-3)
Mass heat capacity [ c^(s), c^(w), c⁽ⁱ⁾ ]	900, 4180, 2000 (Jkg^-1 °C^-1)
Thermal conductivity [ λ^(s), λ^(w), λ⁽ⁱ⁾ ]	1.95, 0.56, 2.24 (Wm^-1 °C^-1)
Poisson’s ratio [ μ ]	0.3
Young’s modulus [ E ]	Unfrozen	11.2 (MPa)
	Frozen (0°C to -1°C)	-2.55T + 11.2 (MPa)
	Frozen (below -1°C)	13.75\|T\|^1.18 (MPa)
Parameters for unfrozen water contents
$\bar{w}, w^{*}$	0.285, 0.058
α, T₀	0.16 (°C^-1), 0 (°C)
Parameters for porosity rate function
$\dot{n}$	1.98·10^-5 (s^-1)
T_m, g_T	-0.82 (°C), 100 (°Cm^-1)
ζ	0.73 (MPa)

열 변형률 증분(dε^th_ij)은 아이스렌즈 형성에 의한 간극률 변화에 따라 정의된다. 여기서 아이스렌즈의 형성은 이방성을 가지며 증가하게 되는데 이를 열 변형률 증분 계산 시 적용시켜야 한다. 해당 개념은 Michalowski(1993)가 ‘Growth tensor’를 도입하여 사용하였으며 Eq. (13)과 같이 정의된다. 여기서 ‘ξ’은 0.33부터 1의 값을 가지며 전자의 값을 사용할 경우 등방성으로 부피가 증가하고, 후자의 값을 사용할 경우 단방향으로 부피가 증가하는 것을 뜻한다.

(13)

\dot{n} = \dot{n} α_{i j} = \dot{n} |\begin{matrix} ξ & 0 & 0 \\ 0 & (1 - ξ) / 2 & 0 \\ 0 & 0 & (1 - ξ) / 2 \end{matrix}|

해당 개념을 도입한 열 변형률 증분을 x, y, z 좌표로 변환하면 Eq. (14)와 같다. 여기서 ‘m=cosθ’, ‘n=sinθ’ 이며 ‘θ’는 x축과 열 유동 방향과의 각도를 의미한다. 최종적으로 Eq. (14)에서 산정된 변형률증분을 서브루틴 UEXPAN 내부 시간 증분 끝(End of time step)에 정의하였다.

(14)

\{\begin{matrix} d ε_{x}^{t h} \\ d ε_{z}^{t h} \\ d ε_{x z}^{t h} \end{matrix}\} = \{\begin{matrix} m^{2} ξ + n^{2} \frac{1}{2} (1 - ξ) \\ n^{2} ξ + m^{2} \frac{1}{2} (1 - ξ) \\ m n (3 ξ - 1) \end{matrix}\} \frac{\dot{n} d t}{1 - n}

4. 수치해석 방법 및 결과

4.1 동결 융기 모델 검토

동상민감성 지반의 동결 융기 모델(Porosity rate function)은 Michalowski and Zhu(2006), Zhang and Michalowski(2015)에 의하여 Fukuda et al.(1997)의 실내 실험 결과와 비교 검증되었다. 해당 실험의 경우 실험 시료의 위 아래면의 온도 조건 및 상재하중을 달리하여 진행되었으며 실험 케이스의 일부분은 Table 2와 같다. 해당 동상민감성 지반의 물성치 및 계수는 Table 1에 정리하였으며 Fig. 7과 같이 동결 융기 모델과 실내 실험 결과가 잘 부합하다는 것을 확인할 수 있다.

Table 2.

Laboratory test cases of frost heave (Fukuda et al., 1997)

Case	Type	Top side temperature (°C)	Bottom side temperature (°C)	Overburden stress (kPa)
A	Step freezing ( test time : 115h )	+5	-5	25
E	Ramped freezing ( test time : 47h )	3-0.042t [ t = time(h) ]	-0.042t [ t = time(h) ]	25
I, J				150, 300
K, L				400, 600

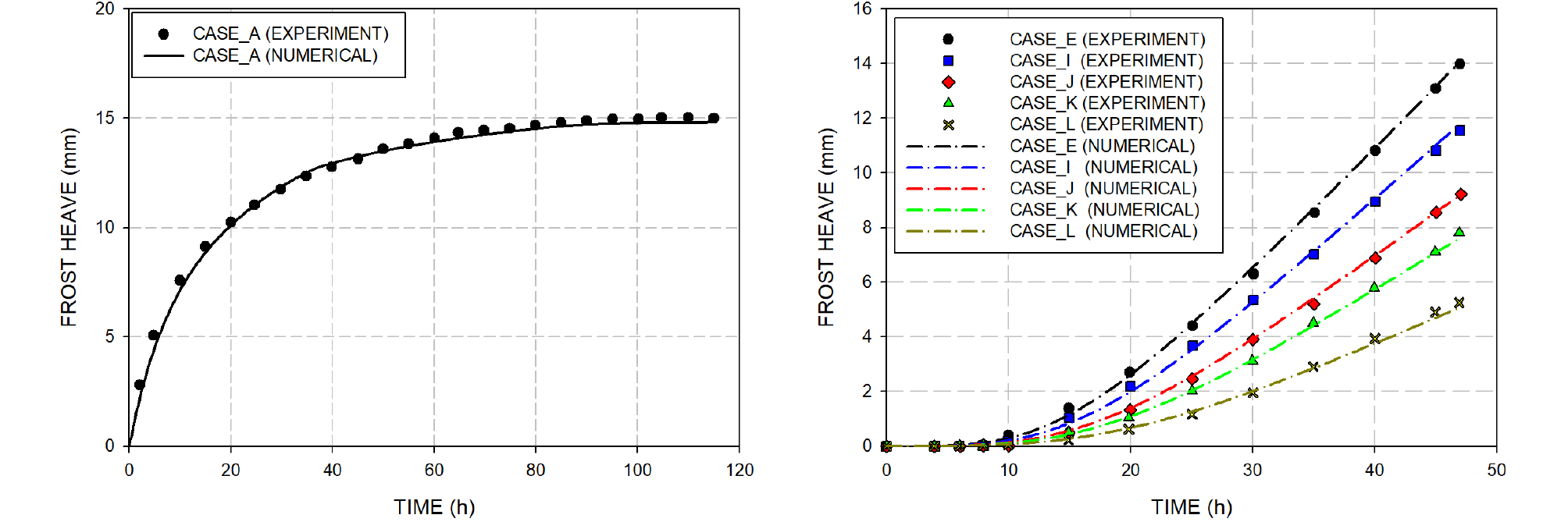
https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F7.jpg

Fig. 7

Comparison between laboratory test results and numerical results (Zhang and Michalowski, 2015)

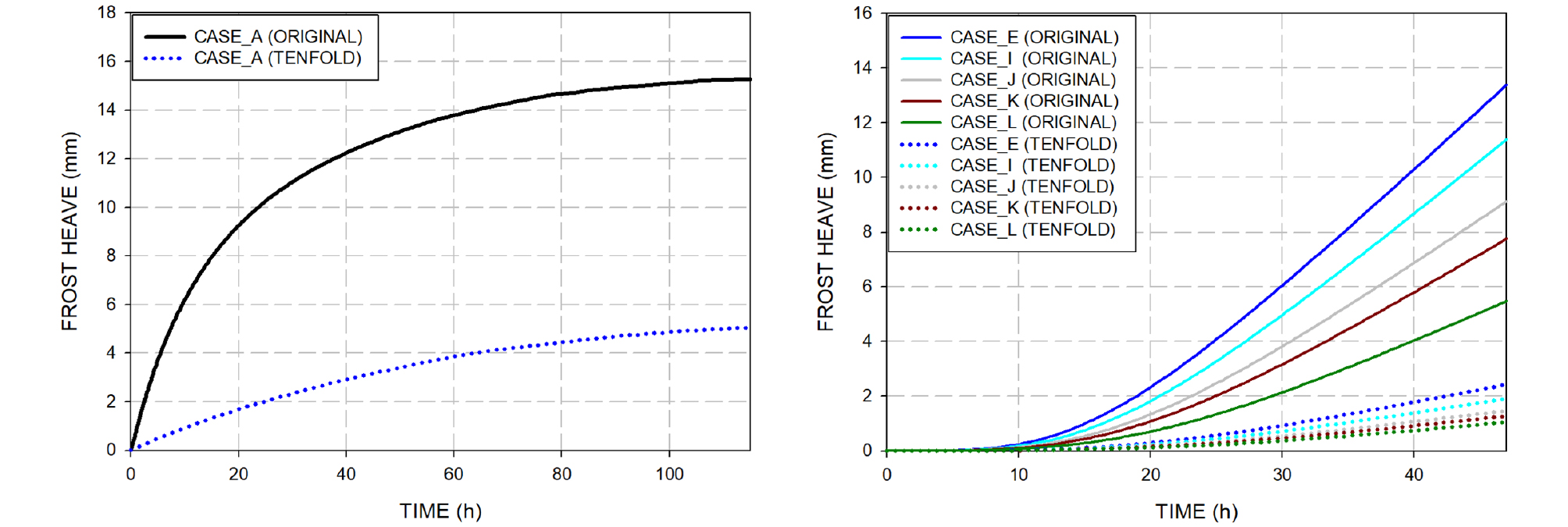
하지만 본 연구에서는 동결 융기 모델의 파라미터 중 최대 간극률 변화율( $\dot{n_{m}}$ )을 10배 작은 값으로 사용하였다. 이는 본 연구의 목적인 열 사이펀의 동결 융기 감소를 확인하는데 있어 과도한 동결 융기로 인한 해석시간의 과도화를 방지하기 위함이다. 해당 파라미터의 사용은 Zhang and Michalowski(2015) 연구에서 사용된바 있으며 이를 참고하였다. 하지만 해당 연구에서는 감소된 ‘ $\dot{n_{m}}$ ’에 대한 동결 융기 경향을 검토하지 않았으므로 본 연구에서는 감소된 ‘ $\dot{n_{m}}$ ’을 사용한 지반의 동결 융기 변화를 사전 해석을 통해 분석하였으며 해석 케이스는 Table 2와 동일하게 진행하였다. 감소된 ‘ $\dot{n_{m}}$ ’값에 따른 동결 융기 차이는 Fig. 8과 같으며, Case A를 기준 약 3배, Case E 기준 6배 정도 감소됨을 확인하였다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F8.jpg

Fig. 8

Comparison frost heave results between using original ‘ $\dot{n}$ ’ and tenfold ‘ $\dot{n}$ ’

4.2 수치해석 모델링 및 케이스

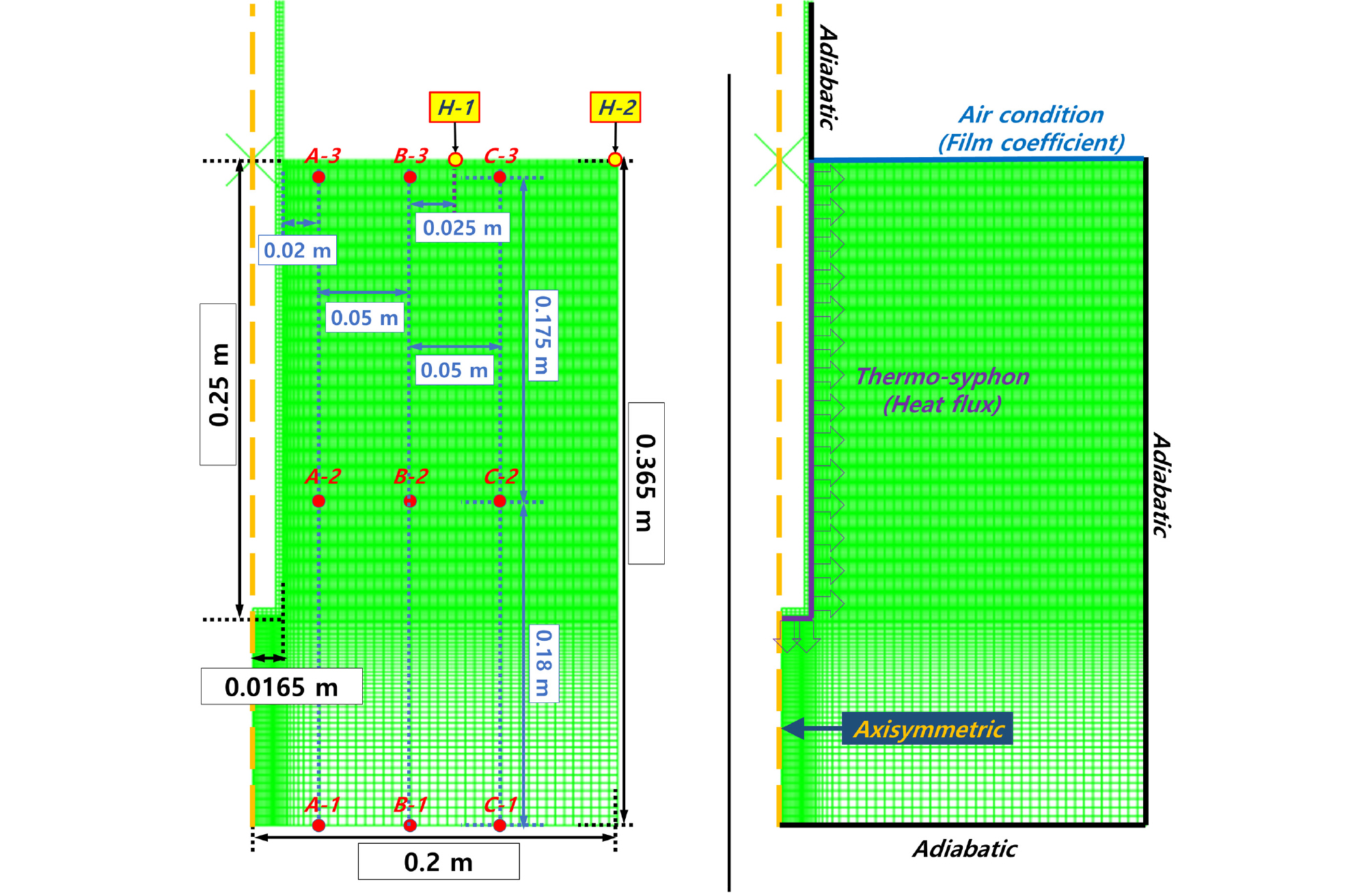
본 연구에서는 기존 실내모형실험(Jang et al., 2014; Lee at al., 2014)과 동일한 제원을 바탕으로 수치해석을 진행하였으며 기존 열 사이펀 수치해석 연구(Park et al., 2021)와 동일하게 Axisymmetric 조건으로 모델링하여 수치해석을 실시하였다. 해당 모델링의 제원과 경계조건은 Fig. 9에 도시하였다. 기존 수치해석 연구 모델링과의 차이는 열 사이펀을 별도로 모델링하여 증발부에만 경계조건을 부여한 것이며 그 외 부분은 단열조건을 부여하였음을 확인 할 수 있다. 이는 2.4절에서 설명한 바와 같이 지반 동결 융기가 진행되면 열 사이펀을 적용한 경계조건 면이 증가하는 문제를 없애기 위함이다. 또한 기존 실내실험 및 수치해석 연구의 측정점은 A-1부터 C-3까지 총 9곳에서의 온도변화를 측정하였지만 본 연구에서는 지반의 동결 융기 검토를 위해 지반 상부에 측정점 두 곳(H-1, H-2)을 추가적으로 두어 결과를 검토하였다. 모델에 사용된 격자는 4절점 Axisymmetric 요소인 CAX4T를 사용하였다. 기존 열 해석 연구와 달리지반의 거동해석이 추가된 본 연구에서는 격자수를 더욱 조밀하게 생성하여 사용하였다. 본 연구의 해석에 사용된 격자는 지반의 상부 및 열 사이펀 부근을 조밀하게 설정하였으며, 격자수는 4860개로 설정하였다.

열 사이펀은 실내모형실험에서 사용된 열 사이펀의 제원을 토대로 모델링 하였으며 외골격 및 냉매의 밀도를 등가 환산하여 충전율에 따른 열 사이펀의 등가 밀도를 부여하였다. 여기서 열 사이펀의 외골격은 밀도 7,850kg m^-3인 강관이며, 내부 냉매는 프레온계 물질로 액체 상태에서 1,201.1kg m^-3의 밀도를 가진다(Park and Lee, 1991).

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F9.jpg

Fig. 9

Geometry condition and boundary condition for numerical analysis

본 연구에서는 총 7가지 케이스해석을 실시하여 열 사이펀에 따른 지반의 동결 융기 억제성능을 평가하였다. 전체 케이스 해석은 동일한 방법으로 수행되었으며 다음과 같다. 먼저 지반의 초기온도를 5℃로 설정 한 후 다음으로 기존 문헌과 동일하게 지반 상부에 3.5Wm^-2K^-1의 대류열전달계수 경계조건을 주어 지반 전체 온도가 영하 13.4℃에 수렴할 때 까지 해석을 수행하였다(Park et al., 2021). 열 사이펀의 경우 선행 연구에서 실시된 열 사이펀 성능(열 사이펀 적용이전, 냉매 충전율 25%, 냉매 충전율 50%, 냉매 충전율 100%)에 따른 케이스 해석을 실시하여 지반의 동결 융기 비교를 실시하였으며, 100% 충전율의 열 사이펀 성능을 임의로 높게 부여한 케이스 3가지를 추가적으로 실시하여 지반의 동결 융기 및 온도변화를 비교하였다. 해당 케이스는 Table 3에 정리하였다. 여기서 열 사이펀의 성능(단위길이당 열전도율, Wm^-1K^-1)은 Eq. (15)에서의 ‘λ_syphon’을 뜻하며 Eq. (15)로 산정된 ‘Q_syphon’은 열 흐름율(heat flow rate)은 식 (5)에 대입되어 해석에 적용된다. Eq. (15)에서 ‘L_evp’, ‘T_evp’, ‘T_con’는 각각 증발부(Evaporator section)의 길이, 증발부 주변 지반의 온도, 응축부(Condenser section) 주변 외기온도를 뜻한다(Park et al., 2021).

Table 3.

Numerical analysis cases

	Existence of thermo-syphon	Filling ratio of refrigerants (%)	Efficiency of thermo-syphon (Wm^-1K^-1)
CASE 1	×	×	x
CASE 2	○	25	0.084
CASE 3	○	50	0.264
CASE 4	○	100	0.464
CASE 4.1	○	100	0.928
CASE 4.2	○	100	1.392
CASE 4.3	○	100	1.856

(15)

Q_{s y p h o n} = λ_{s y p h o n} \times L_{e v p} \times (T_{e v p} - T_{c o n})

4.3 수치해석 결과 및 검토

본 연구에서 수행한 케이스 해석 중 열 사이펀을 사용하지 않은 케이스인 ‘CASE 1’의 온도 하강 경향은 Fig. 10과 같다. 기존 수치해석 연구(Park et al., 2021)의 경우 지반의 온도가 -13.4°C에 수렴 할 때까지 약 700시간이 소요되었지만 본 연구에서는 지반의 온도가 -13.4°C에 수렴하기까지 약 2500시간이 소요되었다. 이러한 시간의 차이는 얼음 띠 형성의 유무로 인한 결과이다. 기존 연구의 경우 동상민감성 지반이 아닌 모래지반으로, 공극빙만 존재하며 얼음 띠가 형성되지 않는다. 반면에 본 연구에서 사용된 동상민감성 지반의 경우 공극빙 형성과 더불어 얼음 띠가 형성되기 때문에 기존 지반에 비해 잠열의 영향이 상당히 커지게 된다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F10.jpg

Fig. 10

Temperature distribution of CASE 1 (a) A-1 (b) A-2 (c) A-3

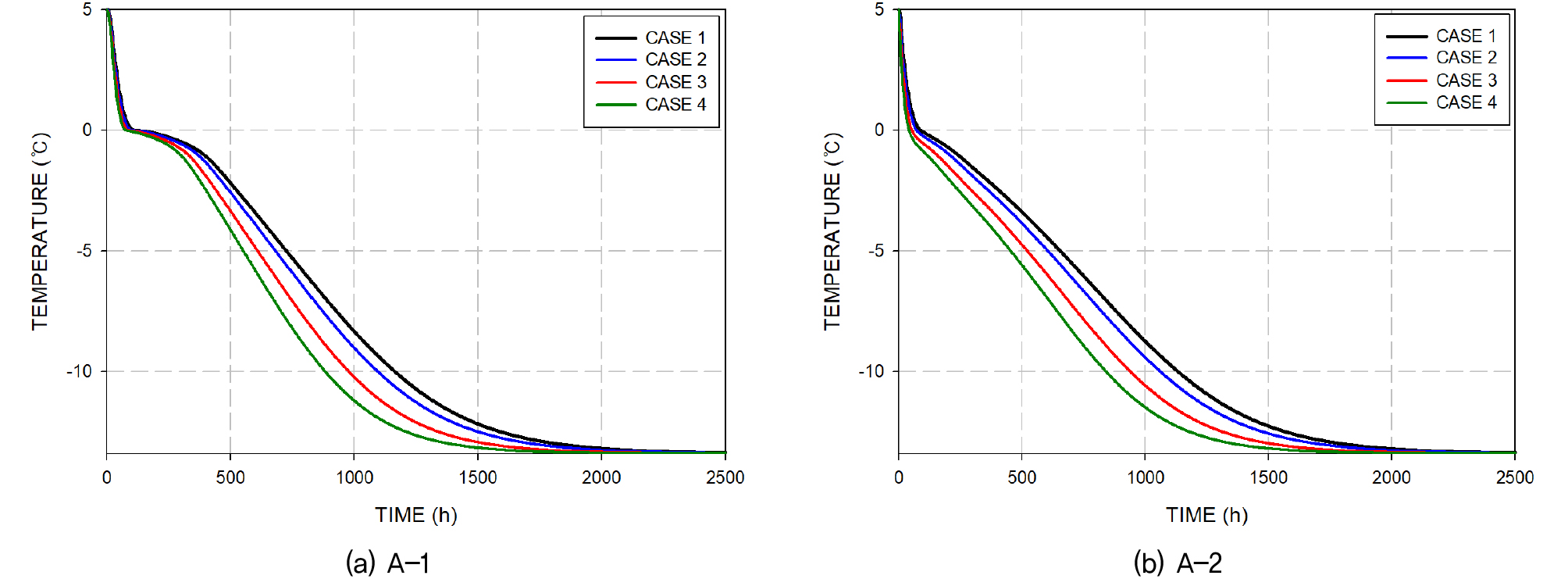
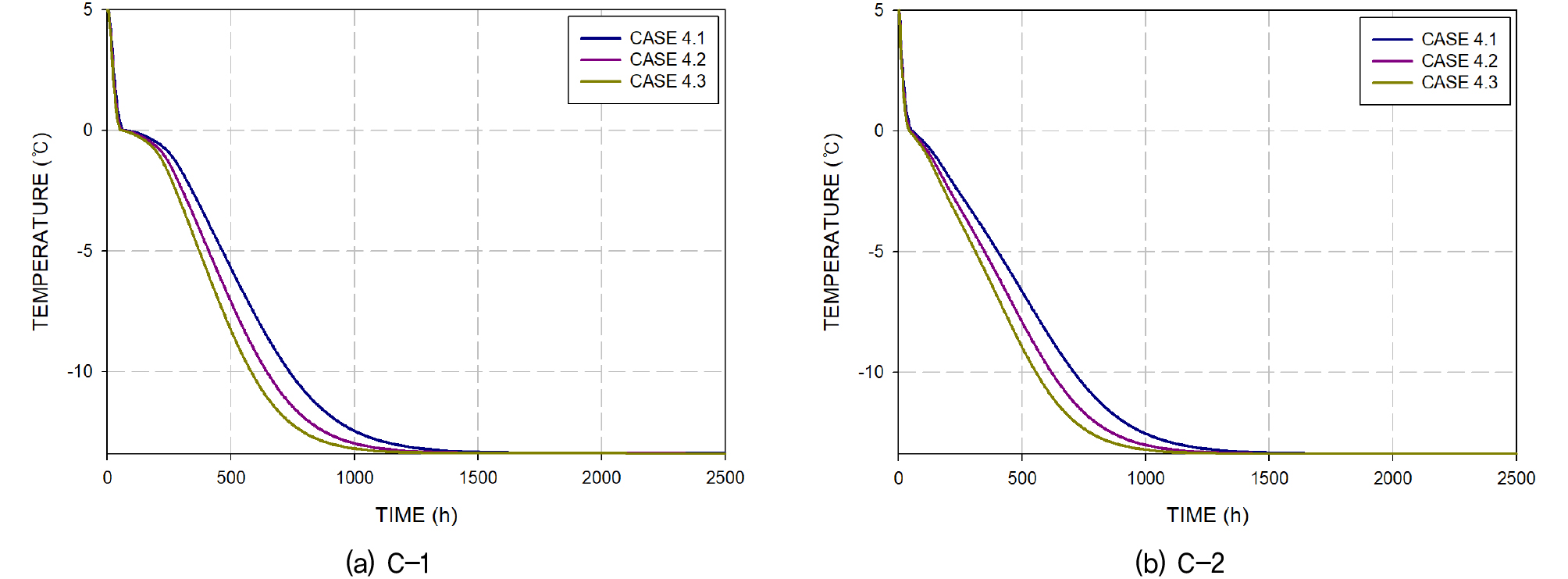
열 사이펀 냉매 충전율에 따른 지반의 온도 추세는 기존 연구와 동일한 결과를 보였다. 충전율 25%, 50%, 100% 케이스인 ‘CASE 2’, ‘CASE 3’, ‘CASE 4’결과를 비교하기 위해 측정점 ‘A-1’ 및 ‘A-2’의 결과를 Fig. 11(a), Fig. 11(b)에 도시하였다. 해당결과를 살펴보면 냉매의 충전율, 즉 열 사이펀의 성능이 증가함에 따라 지반의 온도를 더 급격하게 냉각시키는 것을 확인 할 수 있다. 이러한 경향은 임의로 열 사이펀의 성능을 증가시킨 케이스 ‘Case 4.1’, ‘Case 4.2’, ‘Case 4.3’에도 동일한 결과를 보였으며 측정점 ‘C-1’, ‘C-2’의 결과에서 확인 할 수 있다. 해당 측정점에서의 전체 케이스 결과는 Fig. 12(a), Fig. 12(b)에 도시하였다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F11.jpg

Fig. 11

Temperature distribution results by different filling ratios at (a) A-1 (b) A-2

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F12.jpg

Fig. 12

Temperature distribution results by different performances at (a) C-1 (b) C-2

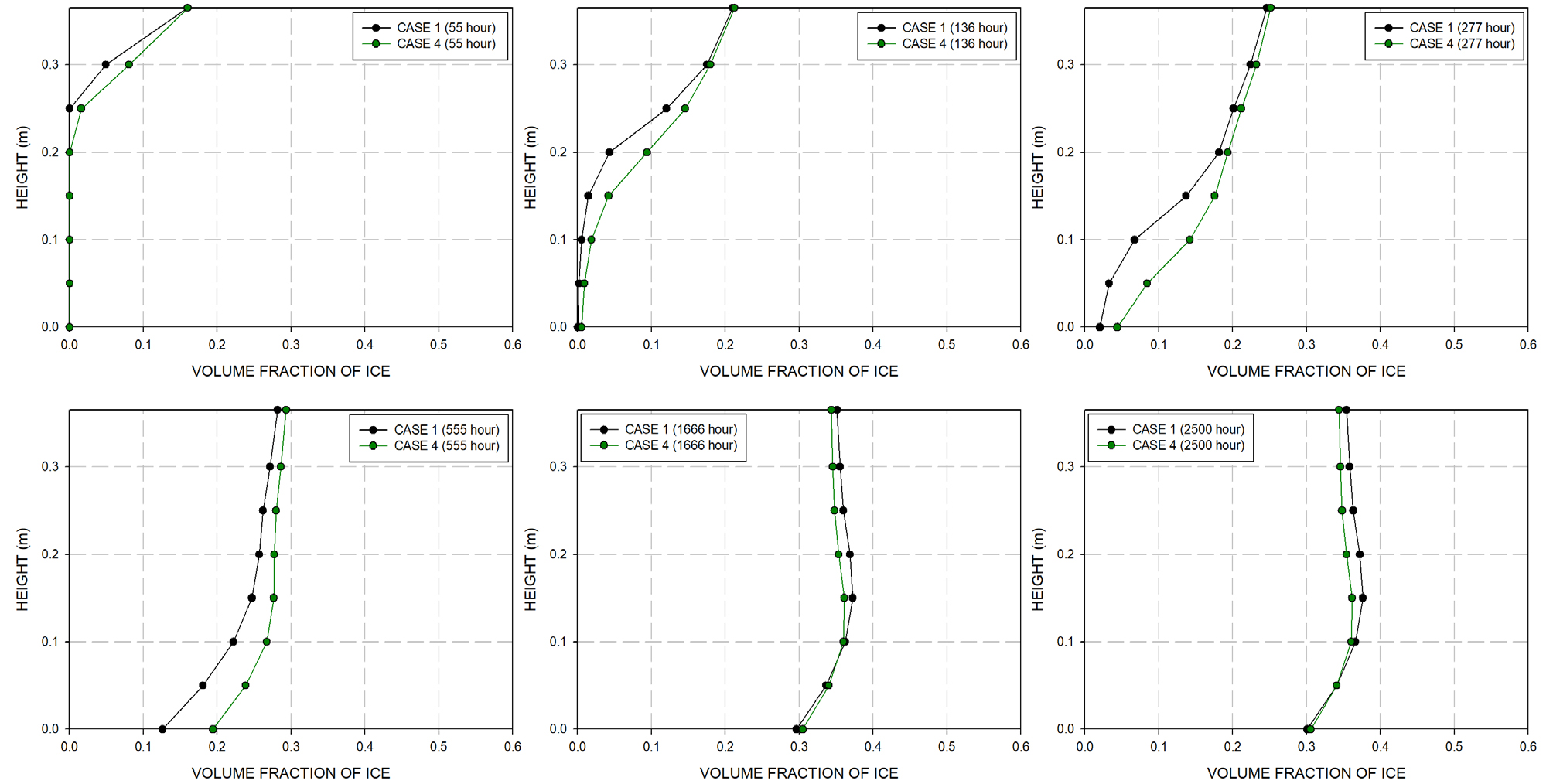
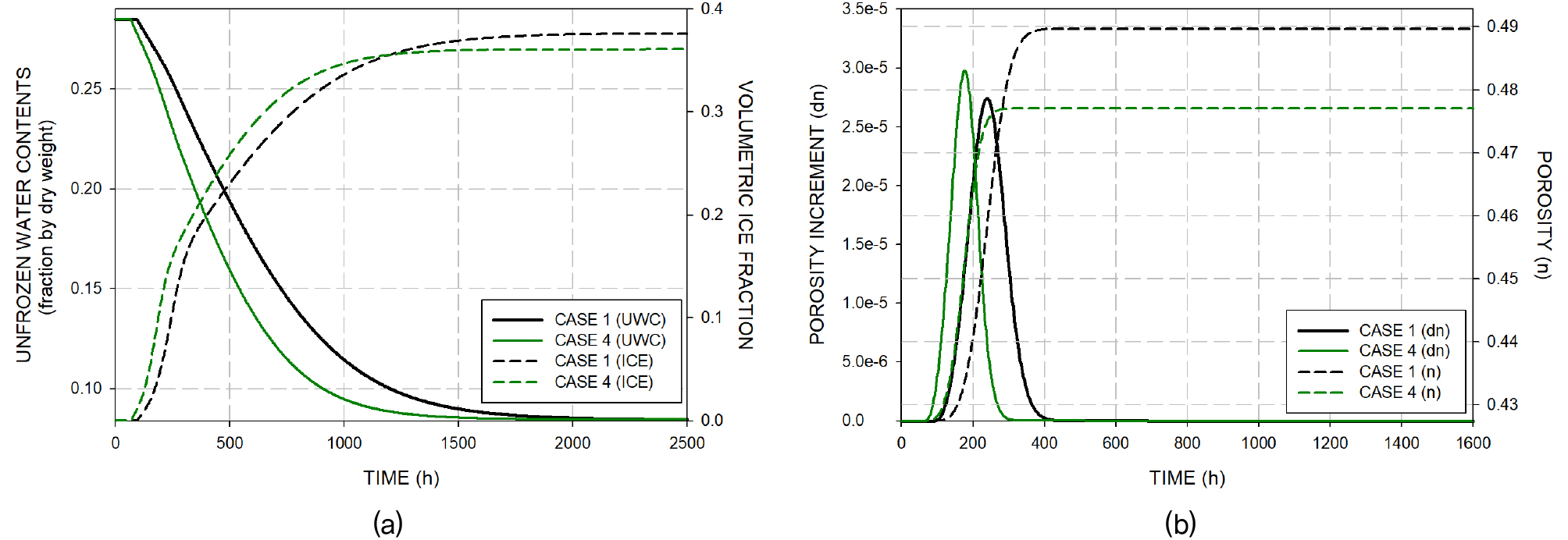
이러한 지반의 온도 하강 차이는 지반의 동결 융기를 저감하는데 큰 영향을 미치며 지반의 깊이별 얼음의 체적분율 생성 경향을 시간별로 나타낸 Fig. 13을 보면 확인할 수 있다. 해당 그래프는 열 사이펀을 적용하지 않은 케이스인 CASE 1과 열 사이펀 적용 케이스인 CASE 4를 비교한 그래프로 해석 중반까지 열 사이펀에 의해 지반의 동결 융기가 활발하게 일어난 CASE 4에서 얼음의 체적분율 생성이 더 빨리 일어나는 것을 확인할 수 있다. 하지만 지반의 온도가 -13.4°C에 수렴되는 후반부에는 CASE 4가 CASE 1에 비해 최종적으로 얼음의 체적분율이 작은 것을 확인 할 수 있다. 이는 본 연구에서 사용된 부동수분경향 및 동결융기모델과 관련이 있다. Fig. 14는 측정점 ‘H-2’ 아래 0.2m 지점의 간극률 증분(dn) 및 간극률(n) 그리고 부동수분 및 얼음의 체적분율을 나타내며 CASE 1, CASE 4 두 케이스를 비교한 그래프이다. Fig. 11과 같이 열 사이펀을 적용한 CASE 4는 CASE 1에 비해 온도가 빠르게 하강한다. 이에 따라 Fig. 14(a)와 같이 부동수분량 또한 빠르게 하강하며 해석 중반까지 CASE 4의 얼음의 체적분율 또한 빠르게 증가한다. 하지만 해석 후반 온도가 수렴하여 두 케이스의 ‘H-2’ 아래 0.2m 지점 온도가 -13.4°C에 수렴하게 되며 부동수분량 크기도 차이가 좁혀지며 결국 수렴하게 된다. 따라서 두 케이스는 동일한 부동수분량을 가지게 되지만 Fig. 14(b)와 같이 CASE 1의 간극률이 상대적으로 더 증가하였기 때문에 얼음의 체적분율이 CASE 4보다 커지게 된다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F13.jpg

Fig. 13

Comparison of ice volume fraction according to using thermo-syphon

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F14.jpg

Fig. 14

Comparison results of (a) Unfrozen water contents and ice volume fraction (b) Porosity increment and porosity

해당 경향은 전체 케이스 결과에서 비교 할 수 있다. 측정점 ‘H-2’ 아래 깊이별 얼음의 체적분율 형성을 시간에 따라 나타낸 결과인 Fig. 15를 보면 열 사이펀 성능이 높을수록 얼음의 체적분율 형성이 작은 것을 확인 할 수 있다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F15.jpg

Fig. 15

Comparison of ice volume fraction according to performance of thermo-syphon

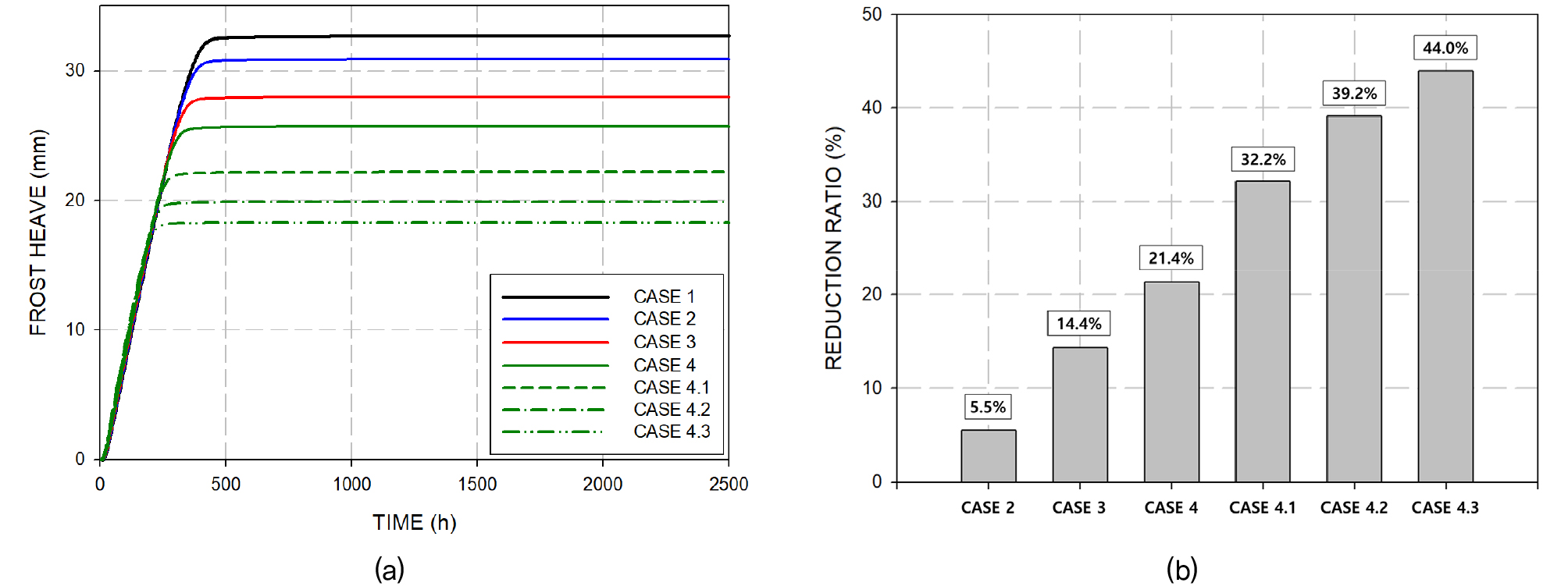
이러한 경향은 총 동결 융기 결과로 이어진다. 열 사이펀을 사용한 케이스는 온도가 빠르게 하강하며 Fig. 14(b)와 같이 간극률 증분(dn)이 좁고 높게 형성되며 열 사이펀을 적용하지 않은 케이스는 온도가 상대적으로 느리게 하강하며 간극률 증분이 상대적으로 낮지만 넓게 형성된다. 최종적으로 열 사이펀을 사용한 케이스는 열 사이펀을 적용하지 않은 케이스에 비해 간극률 형성이 작다. 이러한 경향에 따른 최종 동결 융기 및 동결 융기 감소율은 다음과 같다. Fig. 16은 측정점 ‘H-1’에서의 시간에 따른 동결 융기 변화 및 열 사이펀 적용 이전 케이스대비 동결 융기 감소율을 나타내었다. 해당 결과를 살펴보면, 열 사이펀 적용 이전 케이스인 ‘CASE 1’은 대략 32mm의 동결 융기가 발생하였으며 충전율 100% 케이스인 ‘CASE 4’는 약 25mm로 ‘CASE 1’ 대비 동결 융기가 약 21% 감소되었다. 또한 ‘CASE 4’ 대비 4배의 성능을 가지는 ‘CASE 4.3’의 동결 융기는 약 18mm로 ‘CASE 1’ 대비 44% 동결 융기 감소를 보였다.

https://static.apub.kr/journalsite/sites/kgs/2021-037-10/N0990371003/images/kgs_37_10_03_F16.jpg

Fig. 16

Frost heave results (a) Frost heave results of all cases (b) Reduction ratio of frost heave compared to ‘CASE 1’

5. 결 론

본 연구는 기존 열 사이펀 연구에서 다루지 못한 열 사이펀 성능에 따른 지반의 동결 융기 평가를 수행하기 위해 지반의 동결 융기모델을 추가하였으며 기존 열 사이펀 모델을 변형하여 동결 융기 평가에 적합하게 수정하여 사용하였다. 본 연구를 정리하면 다음과 같다.

(1) 열 사이펀 성능에 따른 지반 동결 융기 평가를 위해 본 연구에서는 ABAQUS 내부 사용자 서브루틴을 통한 TM(Thermo-Mechanical) 모델을 사용하였다. 내부 서브루틴은 시간 증분 끝에서 상태변수들의 상호 영향을 받으며 해석이 진행된다.

(2) 지반의 동결 융기모델은 ‘Porosity rate function’을 사용하였으며 해당 모델은 모세관 현상에 공급되는 간극수의 공급을 온도변화에 따른 간극률의 변화율로 나타낸 모델로 얼음 띠 형성을 정의한다. 이렇게 얼음 띠 형성으로 정의된 간극률은 ‘Unfrozen water contents’ 경향곡선에 따라 흙 내부 3상(흙, 간극수, 얼음)의 체적분율을 결정하고, 3상의 체적분율은 열 물성 및 잠열로 인한 에너지 평형을 계산하게 된다.

(3) 기존 열 사이펀 모델의 경우 열 사이펀을 모델링 하지 않고 열 사이펀과 지반의 경계면에 경계조건을 부여하는 모델이다. 하지만 본 연구에서는 동상민감성 지반을 사용하였으며, 지반이 동결 융기함에 따라 경계면이 지반 동결 융기와 함께 증가하는 문제가 발생하였다. 따라서 본 연구에서는 열 사이펀을 별도로 모델링하여 초기 지반과 열 사이펀의 경계면을 증발부로 설정 해당 섹션에만 경계조건을 부여하였으며 그 외 섹션은 단열조건을 사용하였다.

(4) 열 사이펀 성능에 따른 온도 하강 결과를 살펴보면 기존 연구와 동일하게 열 사이펀 성능이 높아질수록 지반 내부온도가 더 빨리 하강하는 경향을 확인 할 수 있다. 하지만 기존 연구와 달리 -13.4℃에 수렴하기 까지 오랜 시간이 걸리는 것을 확인 할 수 있는데, 이는 얼음 띠 형성에 따른 잠열의 영향 때문이다.

(5) 지반 내부의 얼음의 체적분율을 살펴보면 해석 초반 열 사이펀 성능이 높을수록 급격하게 얼음의 체적분율이 생성되는 것을 확인 할 수 있다. 또한 열 사이펀 성능이 높을수록 얼음의 체적분율 형성이 빨리 끝나며 최종적으로 얼음의 체적분율이 작은 것을 확인 할 수 있다. 이는 지반의 온도가 -13.4℃에 수렴하며 부동수분량 또한 수렴하게 되지만 열 사이펀 성능이 높을수록 간극률이 적게 형성되기 때문이다.

(6) 전체 케이스의 동결 융기를 살펴보면 최종적으로 열 사이펀 적용 이전 케이스인 ‘CASE 1’ 대비 ‘CASE 2’는 5.5%, ‘CASE 3’은 14.4%, ‘CASE 4’는 21%, ‘CASE 4.1’은 32.2%, ‘CASE 4.2’는 39.2% 그리고 ‘CASE 4.3’은 44% 동결 융기 감소율을 보였다.

본 연구는 기존 문헌의 해석 모델 제원을 바탕으로 열 사이펀 성능에 따른 지반의 총 동결 융기를 평가하였다. 하지만 동상민감성 지반에 매립된 수송배관과 같은 구조물은 지반의 총 동결 융기가 아닌 해당 구조물에 영향을 주는 구조물 주변 흙의 동결 융기에 대한 해석이 필요하다. 따라서 추후 다양한 구조물(수송배관, 수송도로, 기초)에 대한 해석을 실시해야 할 것이며, 열 사이펀 성능 외에 열 사이펀의 매립 깊이, 각도에 대한 영향도 추가적으로 평가해야 할 것으로 사료된다.

Acknowledgements

본 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2021R1F1A1051104). 또한 본 연구는 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 사회맞춤형 산학협력 선도대학(LINC+) 육성사업의 연구결과입니다.

References

Abdalla, B. A., Mei, H. X., McKinnon, C., and Gaffard, V. (2016), "Numerical Evaluation of Permafrost Thawing in Arctic Pipelines and Mitigation Strategies", Arctic Technology Conference, Canada. 10.4043/27371-MS

Abdalla, B., Fan, C., McKinnon, C., and Gaffard, V. (2015), "Numerical study of thermosyphon protection for frost heave", OMAE2015-42326, Proceeding of the ASME 34th International Conference on Ocean, Offshore and Arctic Engineering OMAE2015. 10.1115/OMAE2015-42326

Alizadehdakel, A., Rahimi, M., and Alsairafi, A. A. (2010), "CFD Modeling of Flow and Heat Transfer in a Thermosyphon", International Communication in Heat and Mass Transfer, Vol.37, pp.312-318. 10.1016/j.icheatmasstransfer.2009.09.002

Anderson, D. M. and Tice, A. R. (1972), "Predicting unfrozen water contents in frozen soils from surface area measurements", In Frost Action in Soils. Washington, D.C.: National Academy of Sciences, pp.12-18.

Andersland, O. B. and Ladanyi, B. (2004), "Frozen Grouond Engineering 2nd edition", John Wiley&Sons. Inc, pp.322-326.

Fadhl, B., Wrobel, L. C., and Jouhara, H. (2013), "Numerical Modelling of the Temperature Distribution in Two-phase Closed Thermosyphon", Applied Thermal Engineering, Vol.60, pp.122-131. 10.1016/j.applthermaleng.2013.06.044

Fukuda, M., Kim, H., and Kim, Y. (1997), "Preliminary Results of Frost Heave Experiments Using Standard Test Sample Provided by TC8", Proceedings of the International Symposium on Ground Freezing and Frost Action in Soils, Sweden, pp.25-30.

Guymon, G. L., Berg, R. L., and Hromadka, T. V. (1993), "Mathematical Model of Frost Heave and Thaw Settlement in Pavements", CRREL Report 93-2, U.S. Army Corps of Engineers Cold Regions Research and Engineering Laboratory, Hanover, NH.

Hartikainen, J. and Mikkola, M. (1997), "General Thermomechanical Model of Freezing Soil with Numerical Application", Proceedings, International Symposium on Ground Freezing and Frost Action in Soils, Swedin, pp.101-112.

Henry, K. S., Zhu, M., and Michalowski, R. L. (2005), "Evaluation of Three Frost Heave Models", Proceedings Seventh International Conference on the Bearing Capacity of Roads, Railways and Airfields.

Jafari, D., Filippeschi, S., Franco, A., and Marco, P. D. (2017), "Unsteady Experimental and Numerical Analysis of a Two-phase Closed Thermosyphon at Different Filling Ratio", Experimental Thermal of Fluid Science, Vol.81, pp.164-174. 10.1016/j.expthermflusci.2016.10.022

Jang, C. G., Choi, C. H., Lee, J. G., and Lee, C. H. (2014), "Evaluation on Thermal Performance of Thermosyphon by Numerical Analysis", Journal of the Korean Geotechnical Society, Vol.30, No.9, pp.57-66. 10.7843/kgs.2014.30.9.57

Johansen, O. (1975), "Thermal Conductivity of Soils", Ph.D. thesis, Trondheim, Norway, (CRREL Draft Translation 637), ADA044002.

Johnston, G. H., Ladanyi, B., Morgenstern, N. R., and Penner, E. (1981), "Engineering Characteristics of Frozen and Thawing Soils", Permafrost Engineering Design and Construction, John Wiley & Sons.

Kornard, J. M. and Morgenstern, N. R. (1980), "A Mechanistic Theory of Ice Lens Fromation in Fine-Grained Soils", Canadian Geotechnical Journal, Vol.17, pp.473-486. 10.1139/t80-056

Ladanyi, B. and Shen, M. (1993), "Freezing Pressure Development on a Buried Chilled Pipeline", Proc., 2nd Int Symp. on Frost In Geotech. Engrg. (Arvind Phukan, ed.), Balkema, Rotterdam, The Netherlands, pp.23-33.

Lay, R. D. (2005), "Development of a Frost Heave Test Apparatus", Brigham Young University Master of Science dissertation.

Lee, J. G., Lee, C. H., Jang, C. G., and Choi, C. H. (2014), "Experimental and Numerical Investigation of the Performance of Vertical Thermosyphon for Frozen Ground Stabilization", J. Korean Geosynthetics Society, Vol.13, No.4, pp.45-56. 10.12814/jkgss.2014.13.4.045

Li, H., Lai, Y., Wang, L., Yang, X., Jiang, N., Li, L., Wang, C., and Yang, B. (2019), "Review of the State of the Art: Ingeractions between a Buried Pipeline and Frozen Soil", Cold Regions Science and Technology, Vol.157, pp.171-186. 10.1016/j.coldregions.2018.10.014

Michalowski, R. L. (1993), "A Constitutive Model of Saturated Soils for Fros Heave Simulations", Cold Regions Science and Technology, Vol.22, pp.47-63. 10.1016/0165-232X(93)90045-A

Michalowski, R. L. and Zhu, M. (2006), "Frost Heave Modelling Using Porosity Rate Function", Int. J. Numer. Anal. Meth. Geomech., Vol.30, pp.703-722. 10.1002/nag.497

O'Neill, K. and Miller, R. D. (1982), "Numerical Solutions for a Rigid-Ice Model of Secondary Frost Heave", CRREL Report 82-13, U.S. Army Corps of Engineers Cold Regions Research and Engineering Laboratory, Hanover, NH.

Park, D. S., Shin, M. B., and Seo, Y. K. (2021), "Development of Numerical Analysis Model for the Calculation of Thermal Conductivity of Thermo-syphon", Journal of The Korean Geotechnical Society, Vol.37, No.1, pp.5-15

Park, Y. M. and Lee, H. W. (1991), "Calculation of the Thermodynamic Properties of R-134a and A Preliminary Study of the Refrigeration Performance", Korean Journal of air-conditioning and refrigeration engineering, Vol.3, No.4, pp.286-296.

Taber, S. (1930), "The Mechanics of Frost Heaving", J. Geol., Vol.38, pp.303-317. 10.1086/623720

Terzaghi, K. (1952), "Permafrost", Harvard University Press.

Tice, A. R., Anderson, D. M., and Banin, A. (1976), "The Prediction of Unfrozen Water Contents in Frozen Soils from Liquid Limit Determinations", U.S. Army Cold Regions Research and Engineering Laboratory Report CRREL 76-8.

Xu, J., Eltaker, A., and Jukes, P. (2011), "Three-dimensional FE Model for Pipeline in Permafrost with Thermosyphon Protection", Arctic Technology Conference, USA. 10.4043/22098-MS

Zhang, Y. (2014), "Thermal-Hydro-Mechanical Model for Freezing and Thawing of Soils", Doctor of Philosophy (Civil Engineering) in the University of Michigan. 10.1061/9780784412978.025

Zhang, Y. and Michalowski, R. L. (2015), "Thermal-Hydro-Mechanical Analysis of Frost Heave and Thaw Settlement", J. Geotech. Geoenviron. Eng., Vol.141, No.7, 04015027. 10.1061/(ASCE)GT.1943-5606.0001305

Journal of the Korean Geotechnical Society ISSN:1229-2427(Print) 2288-646X(Online) 한국지반공학회 논문집

Preview

Frost Heave of Frost Susceptible Soil According to Performance of Thermo-syphon

ABSTRACT

MAIN

Fig. 1

Characteristic of Freezing soil (Zhang, 2014; Lay, 2005)

(1)

(2)

Fig. 2

Unfrozen water contents (Michalowski, 1993; Park et al., 2021)

Fig. 3

Frost heave results between heave model and experiment (Henry et al., 2005)

(3)

(4)

Fig. 4

Porosity rate by soil type (Michalowski and Zhu, 2006)

(5)

Fig. 5

Issue for thermo-syphon model (a) Non-frost susceptible soil (b) Frost susceptible soil

Fig. 6

User-subroutines for Thermo-mechanical coupling

(6)

(7)

(8)

(9)

(10)

(11)

(12)

Table 1.

Properties and parameters of frost susceptible soil for numerical analysis (Zhang and Michalowski, 2015)

(13)

(14)

Table 2.

Laboratory test cases of frost heave (Fukuda et al., 1997)

Fig. 7

Comparison between laboratory test results and numerical results (Zhang and Michalowski, 2015)

Fig. 8

Comparison frost heave results between using original ‘n˙’ and tenfold ‘n˙’

Fig. 9

Geometry condition and boundary condition for numerical analysis

Table 3.

Numerical analysis cases

(15)

Fig. 10

Temperature distribution of CASE 1 (a) A-1 (b) A-2 (c) A-3

Fig. 11

Temperature distribution results by different filling ratios at (a) A-1 (b) A-2

Fig. 12

Temperature distribution results by different performances at (a) C-1 (b) C-2

Fig. 13

Comparison of ice volume fraction according to using thermo-syphon

Fig. 14

Comparison results of (a) Unfrozen water contents and ice volume fraction (b) Porosity increment and porosity

Fig. 15

Comparison of ice volume fraction according to performance of thermo-syphon

Fig. 16

Frost heave results (a) Frost heave results of all cases (b) Reduction ratio of frost heave compared to ‘CASE 1’

Acknowledgements

References

Comparison frost heave results between using original ‘ $\dot{n}$ ’ and tenfold ‘ $\dot{n}$ ’