1. 서 론
2. 지능형 다짐값의 공간적 분포를 고려한 이상치 분석 기법
3. 현장시험 방법 및 조건
3.1 현장시험 개요
3.2 현장시험 조건
4. 현장시험 결과 및 분석
4.1 다짐횟수에 따른 CMV 분포
4.2 CMV 이상치 분석 기법 실증
5. 결 론
1. 서 론
지능형 다짐(intelligent compaction)이란 다짐롤러에 부착된 센서(고정밀 GPS, 가속도계 등)로부터 얻어진 데이터를 분석해 다짐시공을 최적화하는 기술을 의미한다(Anderegg et al., 2006). 지능형 다짐은 1974년 스웨덴 고속도로 관리국(Swedish Highway Administration)에서 다짐롤러의 진동드럼(vibratory drum)에 가속도계를 부착해 동적 지반반력을 측정하고 이를 지반의 강성과 연관시킨 것으로부터 시작되었다(Thurner and Sandstrom, 1980). 이후 기술적 발전을 거듭한 결과, 계측 분야를 선도하는 업체들(Trimble, Topcon, Leica 등)이 다짐롤러에 장착할 수 있는 애프터마켓(aftermarket) 지능형 다짐 센서 패키지를 출시하였고, 최근에는 건설장비 분야를 선도하는 업체들(Caterpillar, Sakai, Ammann, Bomag 등)이 지능형 다짐 기술이 내장된 다짐롤러를 출시하고 있다.
지능형 다짐 기술의 핵심은 가속도계로부터 측정된 동적 지반반력을 분석해 얻어지는 지능형 다짐값(intelligent compaction measurement value, ICMV)이다. 지능형 다짐값은 다짐롤러 작업 중 실시간으로 도출되고 고정밀 GPS의 측위 정보와 매칭(matching)되어 공간상의 연속적인 데이터로 가공된다. 지능형 다짐값은 현장 지반의 강성에 대한 유용한 정보로써, 다짐롤러 운전자의 효율적인 작업을 지원하거나 혹은 다짐롤러가 스스로 지능적으로 작업할 수 있도록 도와준다. 예를 들어, Ammann의 ACE(Ammann Compaction Expert)는 지능형 다짐값을 기반으로 지반의 강성을 예측하여 다짐롤러 드럼의 진동 주파수(frequency)와 진폭(amplitude)을 자동으로 조절한다. 지반의 강성이 높으면 다짐롤러 드럼의 진동 주파수를 높이고, 진폭을 낮춤으로써 효율적인 다짐이 가능하다.
지능형 다짐 기술의 활용 영역은 다짐시공의 효율화에만 국한되지 않는다. 미국 여러 주 도로국(Department of Transportation, DOT)의 의뢰를 받은 아이오아주립대학교(Iowa State University)의 White 교수와 동료 연구자들을 중심으로 지능형 다짐값을 다짐 품질 지표로 활용하기 위한 연구가 수행되어 왔다(Thompson and White, 2007; White and Thompson, 2008; White et al., 2008; Vennapusa et al., 2010; Meehan et al., 2017). 일반적으로 다짐 품질관리에는 평판재하시험을 통해 얻은 지지력 계수 혹은 현장 밀도시험을 통해 얻은 상대 다짐도가 이용된다(KCS 11 20 20, 2023). 평판재하시험 및 현장 밀도시험은 다짐공정이 완료된 후 특정한 지점에서 수행되는데, 품질시험을 위한 작업 대기시간이 발생되고 넓은 영역의 품질을 한 지점의 측정값이 대표하게 되어 토공사의 생산성 및 품질 저하의 주요 원인으로 지목되고 있다(Baek et al., 2020). 반면, 지능형 다짐값은 다짐롤러 작업 중 실시간-연속적으로 도출되는 현장 지반의 강성 정보이므로, 지능형 다짐 기술을 통해 기존 다짐 품질관리 방법의 한계(비실시간-불연속적)를 극복할 수 있을 것으로 기대된다. 그러나 지능형 다짐값을 주요한 다짐 품질 지표로 활용한 실규모 현장은 찾아보기 어렵다. 상술한 연구들을 통해 지능형 다짐값이 다짐 품질을 나타내는 지표로 사용할 수 있음이 확인되었지만, 지능형 다짐값의 처리 및 분석 절차는 명확히 확립되지 못했기 때문이다.
특히, 전체 시공영역에 대해 연속적으로 측정되는 지능형 다짐값의 변동성이 문제가 되고 있다. 본 저자가 국내 현장에서 수행한 연구(Choi et al., 2021; Baek et al., 2023; Baek et al., 2024a; Baek et al., 2024b)와 아이오아주립대학교의 White 교수가 미국의 미네소타 주에서 수행한 연구(White et al., 2007)에서는 동일 조건에서 측정된 지능형 다짐값의 변동계수(coefficient of variation, CV)가 매우 높음(20~40%)을 공통적으로 지적하고 있다. 지능형 다짐값은 지반조건(입도, 함수비, 강성 등)과 다짐롤러 구동조건(속도, 진동수, 진폭, 지반-드럼 접촉상태 등)에 영향을 받는다(Cao et al., 2021). 이들을 시공영역 전체에 걸쳐 균질하게 유지시키는 것은 사실상 불가능하기 때문에 지능형 다짐값의 변동계수가 매우 높게 나타나는 것이다(Baek et al., 2024b). 지능형 다짐값 기반의 다짐 품질관리를 위해서는 다짐 품질과 관계없는 다짐롤러의 구동조건이 지능형 다짐값에 미치는 영향을 배제해야 한다. 또한 다짐 품질과 직접적인 관계가 있는 지반조건의 내재적 불균질성을 고려하여 지능형 다짐값의 허용할만한(acceptable) 변동계수 범위를 결정해야 한다.
상술한 문제를 해결하기 위해서 본 연구에서는 지능형 다짐값의 공간적 분포를 고려한 이상치 분석 기법을 제안했다. 이상치 분석 기법을 통해 다짐 품질과 관계없는 다짐롤러의 구동조건 변화가 지능형 다짐값에 미치는 영향을 배제함으로써, 지능형 다짐값의 과도한 변동성과 관련한 문제를 보완할 수 있도록 했다. 한국건설기술연구원 SOC 실증연구센터(경기도 연천시 소재)에서 현장시험을 수행해 대표적인 지능형 다짐값인 CMV(Compaction Meter Value)를 획득하고, 이를 통해 본 연구에서 제안한 이상치 분석 기법을 실증하고, 지반의 내재적 불균질성에 따라 나타나는 지능형 다짐값의 변동성에 대해 고찰했다.
2. 지능형 다짐값의 공간적 분포를 고려한 이상치 분석 기법
데이터 품질 분석은 신뢰성 높은 분석 결과를 얻기 위해 초기 단계에서 수행되는 중요한 과정이다. 데이터 과학 분야에서는 데이터 품질의 중요성을 강조하기 위해 “GIGO(Garbage in, Garbage Out)”라는 표현이 자주 사용된다. 이는 입력 데이터의 정확성이 높을수록 유의미한 결과를 도출할 수 있음을 의미한다. 따라서 신뢰성 높은 결과를 위해서는 변수 분포의 전체 패턴을 벗어나 비정상적으로 존재하는 데이터를 이상치로 간주하고, 분석 전에 적절히 처리하는 것이 필수적이다(Kwak and Kim, 2017). 즉, 변동성이 큰 데이터에는 다수의 노이즈가 존재하며, 이를 최소화하기 위해 이상치(outlier)를 처리해야 한다. 이상치는 통계적으로 자료값들이 주로 모여 있는 곳에서 멀리 떨어져 있는 관측치로 정의된다(Kim, 2006).
대표적인 이상치 분석 기법으로는 표본 평균과 표준편차를 기반으로 한 3-sigma 법칙(Daw et al., 1972; Moivre, 2013), 정규성을 가정하지 않는 boxplot 법칙(Tukey, 1977) 등이 있다. 3-sigma 법칙은 충분히 큰 표본이 존재하여 데이터의 정규성을 합리적으로 가정할 수 있을 때 정확성이 높지만, 표본의 크기가 작고 극단적인 이상치가 존재하면 크게 왜곡될 수 있다(Leys et al., 2013; Lightfoot and O’Connell, 2016; Santos, 2020). Boxplot 법칙은 변수 분포에 대한 특별한 가정이 없는 일반적인 경우에 간단하면서도 효율적으로 이상치를 탐색할 수 있지만, 데이터의 왜도 정도에 따라 편향될 수 있으므로 주의가 필요하다(Hubert and Vandervieren, 2008; Santos, 2020).
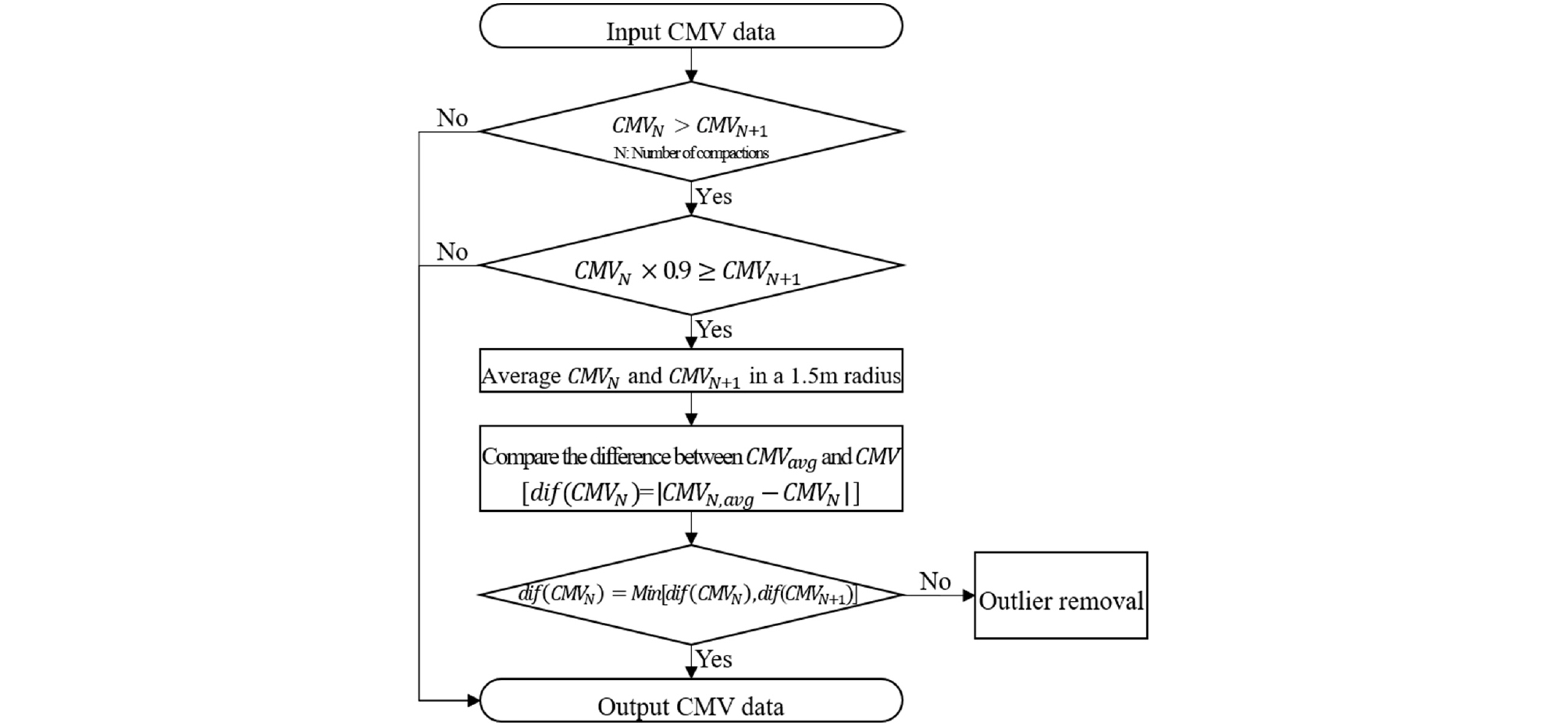
지능형 다짐값은 지반조건과 다짐롤러 구동조건에 영향을 받아 높은 변동성을 나타낸다(Cao et al., 2021). 품질 지표의 변동성은 넓은 시공영역을 한 지점의 측정값(지지력 계수, 상대 다짐도)으로 관리하는 종래의 다짐 품질관리 방법에서는 고려하지 않았던 사항으로, 지능형 다짐값을 사용함에 따라 품질 지표의 변동성이 기록된다면 시공자와 공사감독자 간 상당한 다툼(argue)의 여지가 있을 것으로 예상된다(Baek et al., 2023). 따라서 지능형 다짐값 데이터의 특성을 고려해 적절한 방식으로 이상치를 제거하고 내재적 요인(즉, 지반의 내재적 불균질성)으로 인해 나타나는 변동성의 크기를 평가해야 한다. 지능형 다짐값에 영향을 미치는 두 가지 요인 중, 지반조건의 변화는 다짐 품질과 직접적인 관련이 있으므로 지능형 다짐값을 통해 기록해야 하는 중요한 사항이다(White et al., 2007). 따라서 이상치를 제거할 때는 다짐 품질과 관계없는 다짐롤러 구동조건의 변화에 따른 영향만을 배제하는 것이 적합하다. 그러나 상술한 대표적 이상치 분석방법들과 같이 데이터 분포에서 극단적으로 큰 값과 작은 값을 제거하는 방식으로는 지반의 내재적 불균질성에 따른 다짐 품질의 변동성을 제대로 고려할 수 없다. 따라서 본 연구에서는 이상치 분석을 위해 3가지 조건(① 지능형 다짐값은 다짐횟수(즉, 다짐도)가 증가함에 따라 증가, ② 다짐롤러 구동조건이 변화하면 지능형 다짐값이 급격하게 변화, ③ 지능형 다짐값은 인접한 지역에서 측정된 값들과 공간적 상관성 높음)을 가정하고, 최적 이상치 분석 기법을 제안했다(Fig. 1). 본 연구에서는 대표적인 지능형 다짐값인 CMV를 이용했으므로 Fig. 1에서 CMV로 표시했다.
제안된 이상치 분석 기법의 초기 단계에서는 가정조건 ①을 고려하여 특정 위치에서 측정된 지능형 다짐값이 다짐횟수 증가에도 불구하고 일정하거나 감소하는 값을 식별하였다. 다짐횟수가 증가하였음에도 지능형 다짐값이 감소하는 현상은 가정조건 ②와 같이 다짐롤러 구동조건(속도, 진동수, 진폭, 지반-드럼 접촉상태 등) 변화에 기인하므로(Caicedo, 2018; Baek et al., 2024b), 이상치로 판단하는 것이 합리적이다. 다만, 본 저자가 국내 현장에 CMV를 적용했던 경험에 따르면(Baek et al., 2024a; Baek et al., 2024b), 현장에서는 다짐 중 지반조건(다짐에너지에 의한 입도 변화 및 기상 변화에 따른 함수비 변화)이 변화하는 등의 이유로 CMV는 약 1~2 정도의 변동(fluctuation)을 보일 수 있다. 이에 따라 다짐횟수가 증가해도 다짐값이 비례하여 증가하지 않는 예외 상황이 발생할 수 있으므로, 직전 다짐횟수에 비해 CMV 값이 급격하게 감소(10% 이상 감소)한 경우만을 추출해 이상치 분석에 사용했다.
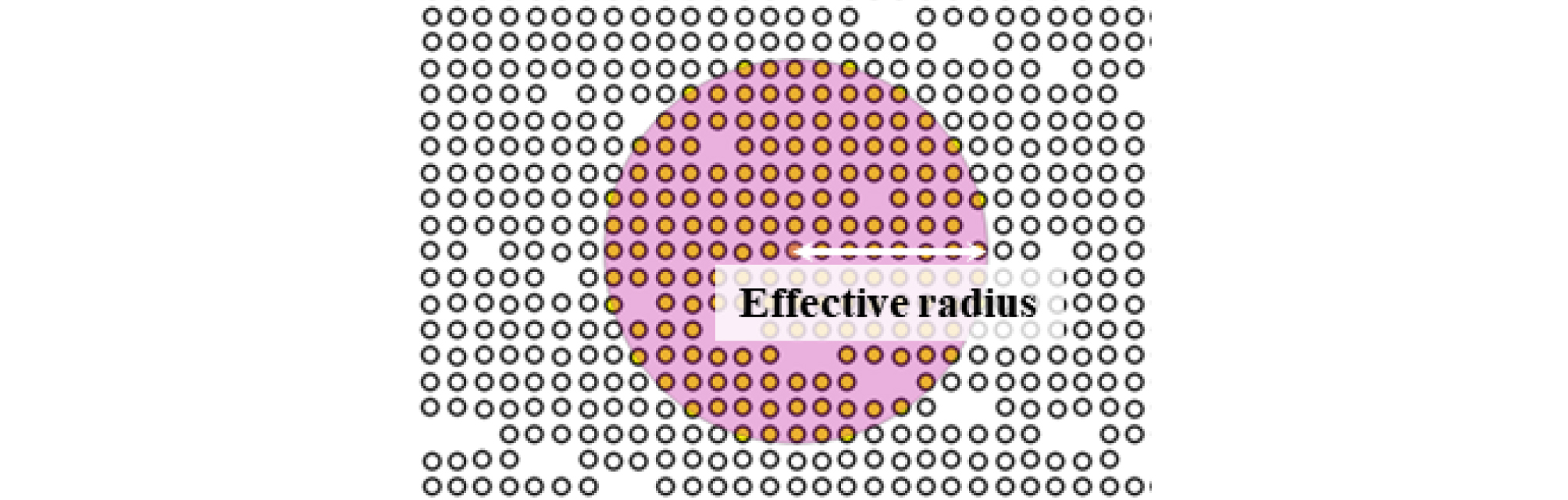
만약 지능형 다짐값의 급격한 감소가 N+1번째에서 나타났다면, 이는 N번째 다짐횟수에서 매우 큰 값이 나타나서 N+1번째의 값이 급격히 감소하는 경우(N번째 다짐횟수에서 측정된 값이 이상치)와 N번째는 정상적인 값이지만 N+1번째의 값이 매우 작게 측정되는 경우(N+1번째 다짐횟수에서 측정된 값이 이상치)로 나눠볼 수 있다. 따라서 N번째 혹은 N+1번째 측정값 중 어느 값을 이상치로 판단할지에 대한 추가적인 분석이 필요하다. 지반조건은 깊이와 위치에 따라 불균질성을 보이지만 자기 상관거리가 작을수록 유사성을 나타낸다(Choe, 2013). 자기 상관거리는 서로 다른 위치에서 얻은 동일 변수에 대해 거리에 따른 상관관계를 나타낸 것이다. 즉, 지능형 다짐값은 가정조건 ③과 동일하게 지반조건의 영향으로 인해 인접 지역에서 높은 공간적 상관성을 보이며 유사성을 가진다. 따라서 Fig. 2와 같이 N번째와 N+1번째 측정값에 대해 각각 유효반경(측정값을 중심으로 하여 측정값에 영향을 미치는 범위를 나타내는 반경)을 그리고, 유효반경 내 지능형 다짐값의 평균과의 차이가 더 큰 값을 이상치로 판단해 제거했다.
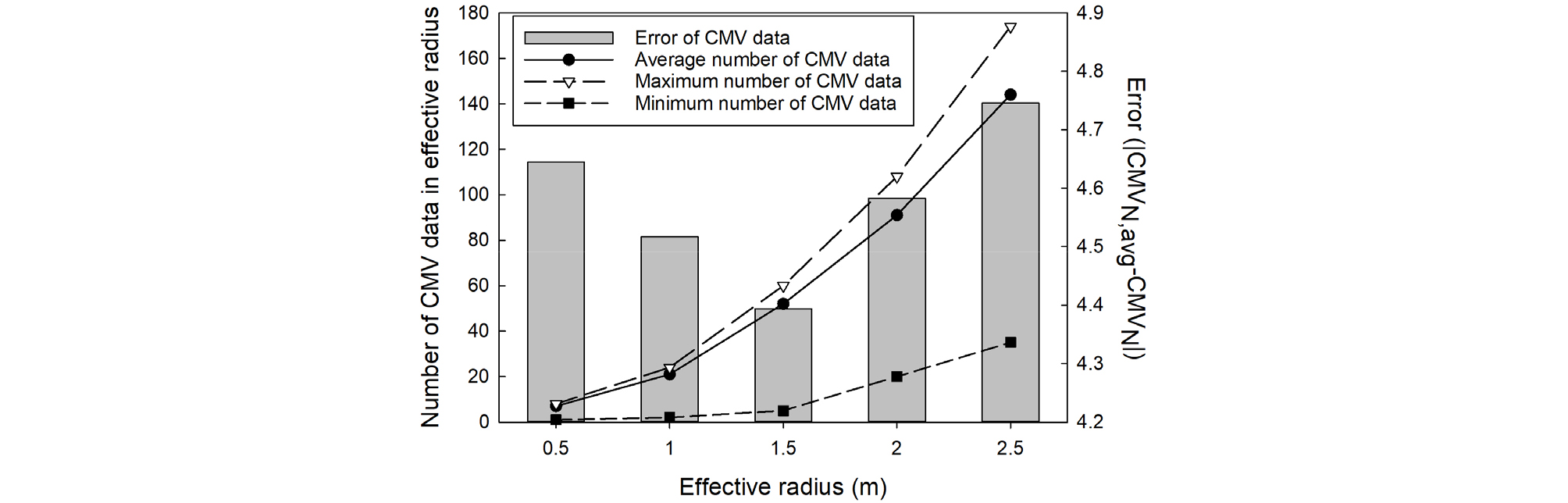
이상치 제거 결과는 유효반경의 크기에 따라 달라질 수 있다. 본 연구에서 수행된 현장시험으로부터 획득한 지능형 다짐값을 이용해 최적 유효반경을 찾기 위한 분석을 수행했다. Fig. 3과 같이 유효반경을 0.5m, 1.0m, 1.5m, 2.0m, 2.5m로 변화시켜가며, 유효반경 내에 존재하는 지능형 다짐값의 최대 개수, 평균 개수, 최소 개수와 유효반경 내 평균값과 중심값 간의 오차를 비교했다. 작은 유효반경 적용 시, 반경 내 포함된 지능형 다짐값의 개수가 너무 적어 비교가 어려운 경우가 발생하여 지능형 다짐값의 최소 개수가 유효반경 결정에 중요한 요소임을 확인했다. 또한 유효반경 내 평균값과 중심값의 오차를 산정한 결과, 1.5m 유효반경 적용 시 약 4.4의 최소 오차를 보였다. 따라서 지능형 다짐값의 유효반경을 1.5m로 설정하고 이상치 분석에 적용했다. 추후 타지역에 적용하여 유효반경 설정 시, Fig. 3과 같은 분석을 사용하면 정확성을 높일 수 있으나 CMV값이 측정되는 간격(0.3m) 및 데이터의 갯수 분포를 고려하면 1~2m의 유효반경을 사용해도 무방할 것으로 판단된다.
3. 현장시험 방법 및 조건
3.1 현장시험 개요
본 연구에서 제안된 이상치 분석 기법을 실증하기 위해서 지능형 다짐 장치가 부착된 다짐롤러를 이용해 현장시험을 수행했다. 현장시험 부지는 한국건설기술연구원 SOC 실증연구센터(경기도 연천시 소재)에 위치했다. 너비와 길이가 각각 15m 및 25m인 시험부지에 성토재료를 0.5m 두께로 균질하게 포설한 뒤, Bomag의 BW211D 다짐롤러(총 중량 10,600kg, 드럼 하중 5,670kg, 드럼 직경 1.5m, 드럼 너비 2.13m, 가진 주파수 범위 30-34Hz)를 이용해 다짐했다(Fig. 4). 다짐롤러의 다짐 영향깊이는 지표면으로부터 약 1.0~1.2m이며, 이 범위 내 지반의 강성이 지능형 다짐값에 영향을 준다(White, 2008). 따라서 성토재료 포설 전 화강풍화토로 구성된 원지반(underlying layer)을 왕복 3회 다짐하여 원지반의 불균질한 다짐 상태가 지능형 다짐값에 미치는 영향을 최소화했다. 다만, 원지반의 불균질한 상태(동남쪽에 자갈이 다수 분포하고 북서쪽에 함수비가 높음)가 육안으로 관찰되어 현장시험 결과에 영향을 줄 것으로 예상되었다.
본 연구에서는 지능형 다짐값을 획득하기 위해서 Trimble의 지능형 다짐 센서 패키지인 CCSFlex를 사용했다. CCSFlex를 구성하는 요소인 고정밀 GPS와 가속도계를 각각 다짐롤러 캐빈(cabin) 상단과 드럼의 회전축에 부착했다(Fig. 3(b)). 고정밀 GPS는 Trimble VRS(Virtual Reference System)를 통해 고정밀 좌표를 초당 1개씩 도출했다. 가속도계는 내장된 시스템을 통해 대표적인 지능형 다짐값인 CMV를 산출했다. 산출된 CMV 값은 고정밀 GPS의 측위 정보와 매칭되어 0.3m × 0.3m 격자형의 셀마다 하나씩 저장되었다.
다짐롤러는 드럼을 통해 동적하중을 가하여 지반을 다짐한다. CMV는 드럼과 지반 사이의 동적 상호작용(dynamic interaction)을 분석해 얻어지는 무차원(dimensionless)의 값이다. CCSFlex의 가속도계는 내장된 시스템을 통해서 (1) 드럼에 부착된 가속도계를 통해 진동다짐 중 가속도 값을 측정하고; (2) 시간이력에 따라 측정된 가속도 값을 고속 푸리에 변환(Fast Fourier Transform, FFT)을 통해 주파수 도메인(frequency domain)으로 변환하고; (3) Eq. (1)을 통해 CMV를 산정한다.
여기서, A0과 A1은 각각 드럼에 부착된 가속도계로부터 얻은 시간 이력 가속도의 첫 번째 조화성분의 진폭과 두 번째 조화성분의 진폭을 의미한다(Sandstrom and Pettersson, 2004).
즉, CMV는 진동롤러의 가진 주파수인 기본 주파수 성분(fundamental frequency)에 해당하는 첫 번째 조화성분의 진폭과 두 번째 조화성분의 진폭의 비율을 통해 산정되는 값이다. 지반의 강성이 증가함에 따라 지반의 동적 반발력이 커져 두 번째 조화성분의 진폭이 증가하는 경향을 보이므로, CMV 값은 지반의 강성이 증가함에 따라 증가한다(Thompson and White, 2007; White and Thompson, 2008; White et al., 2008; Vennapusa et al., 2010; Meehan et al., 2017). 그러나 CMV를 포함한 대부분의 지능형 다짐값은 지반의 강성뿐만 아니라 성토재료의 상태(입도, 함수비 등) 및 다짐롤러의 구동조건 등에 따라 크기가 달라진다(Baek et al., 2020; Cao et al., 2021; Choi et al., 2021). 따라서 지능형 다짐과 관련한 국내외 규정(RVS, 1999; ROAD, 1994; ISSMGE, 2005; FHWA, 2014; KCS 10 20 70, 2021)에서는 시공영역 전체에 걸쳐 성토재료의 상태 및 다짐롤러의 운용조건을 일정하게 유지하도록 명시하고 있다. 그러나 지반의 내재적 불균질성에 따라 성토재료의 상태는 위치에 따라 다르며, 다짐롤러 전진-방향전환-후진을 반복하며 시공하기 때문에 구동조건이 수시로 변화한다. 이에 따라 CMV 값은 필연적으로 높은 변동성을 보인다. 본 연구에서는 제안된 이상치 분석 기법을 통해 다짐 품질과 관련이 없는 요소로 인해 나타나는 CMV의 변동성을 제거하고, 내재적 요인(즉, 지반의 내재적 불균질성)으로 인해 나타나는 변동성의 정도를 확인했다.
3.2 현장시험 조건
시험부지에 포설된 성토재료를 지능형 다짐 장치가 부착된 다짐롤러를 이용해 다짐하며 CMV를 획득했다. 성토재료는 너비 방향으로 일곱 개의 레인(lane)으로 나누어 다졌는데(Fig. 4(a)), 각 레인의 너비는 다짐롤러 드럼의 너비(2.13m)와 동일했다. 다짐롤러는 드럼을 통해 지반에 진동하중을 가하며 각 레인을 길이 방향으로 총 6회 왕복(전진 및 후진)했다. 다짐롤러가 방향을 전환하거나 정지하는 경우를 제외하고는 속도, 가진 주파수, 진폭을 각각 3.0km/h, 31.8Hz, 0.8mm로 일정하게 유지했다. 지반의 강성(혹은 다짐도)에 관계없이 드럼의 가진 주파수 및 진폭을 일정하게 유지했기 때문에, 일부 강성이 높은 위치에서 다짐 중 지반-드럼 접촉상태가 불량(double jump 혹은 rocking motion)한 현상이 관찰되었다.
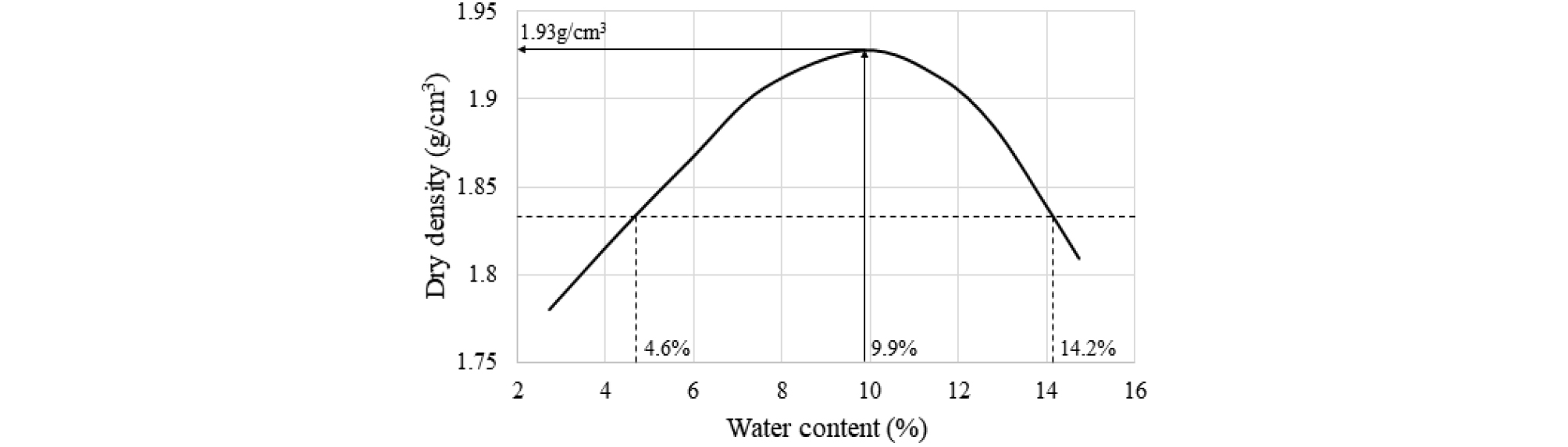
성토재료로는 국내 토공사 현장에서 실제로 사용되고 있는 화강풍화토가 사용되었다. Table 1은 본 연구에서 사용된 성토재료의 기본 물성값을 나타낸다. 성토재료는 4번체와 200번체 통과량이 각각 91.2%와 14.3%였고, 통일분류법(Unified Soil Classification System, USCS)에 따라 SM(실트질 모래)으로 분류되었다. Fig. 5는 KS F 2312(2022)에 따라 수정다짐시험을 수행해 얻은 성토재료의 다짐곡선이다. 성토재료의 최대 건조단위중량과 최적 함수비는 각각 1.93g/cm3과 9.9%로 평가되었고, 상대 다짐도 95%를 달성할 수 있는 함수비 범위는 4.6~14.2%였다. 다짐 전 각 레인의 가운데에서 채취한 시료를 이용해 현장 함수비를 측정한 결과, 평균 함수비 8.2%(6.0~10.1%)로 상대 다짐도 95%를 달성할 수 있는 범위 내에 있었다.
4. 현장시험 결과 및 분석
4.1 다짐횟수에 따른 CMV 분포
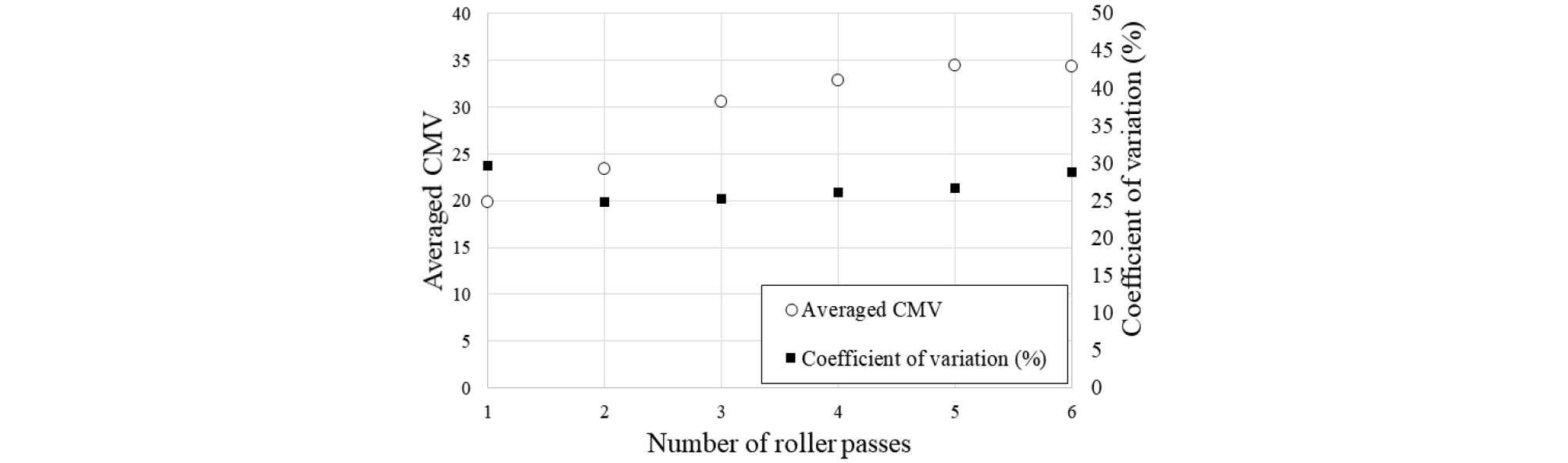
Fig. 6은 현장시험을 통해 획득한 CMV의 평균값과 변동계수(특정 다짐횟수에서 얻어진 CMV의 평균값에 대한 표준편차의 비율)를 다짐횟수에 따라 나타낸 것이다. CMV는 다짐롤러의 진행방향(전진 혹은 후진)에 따라 “미묘한(subtle)” 영향을 받는다고 알려져 있으므로(Mooney et al., 2010; Baek et al., 2024a), 본 연구에서는 왕복(전진 및 후진) 1회마다 측정된 CMV의 평균값을 분석에 활용했다(총 6회 왕복했으므로 최종 다짐횟수는 6회).
Fig. 6에서 확인할 수 있듯이, 다짐횟수가 증가할수록 지반의 평균적인 강성이 증가하여 CMV의 평균값이 증가하는 경향(19.8~34.4)을 보였다. 다짐횟수 증가에 따른 CMV 평균값의 증분은 점차 감소했는데 다짐의 효과가 초기 다짐횟수에서 크게 나타났다. 특히 다짐횟수 5회와 6회에서 측정된 CMV 평균값은 거의 차이가 없었다. CMV의 변동계수는 24.7~29.6% 범위에 존재하여, 기존 연구(White et al., 2007; Baek et al., 2024a; Baek et al., 2024b)와 비슷한 값을 나타냈다. 초기 다짐횟수(1~3회)에서는 변동계수가 점차 작아져서 다짐 품질의 위치별 변동성이 감소했지만, 후기 다짐횟수(4~6회)에서는 오히려 변동계수가 반등했다. 변동계수에 대한 절대적인 기준은 확립되어 있지 않으나, 여러 문헌들(Brown, 1998; Kumar et al., 2023)은 변동계수 30%를 높은 변동성의 기준으로 활용하고 있다. 이에 비춰볼 때, CMV의 변동성은 높은 수준으로, 모든 다짐횟수에서 다짐 품질의 위치별 변동성이 높게 나타남을 의미한다.
이와 같은 CMV의 평균값 및 변동계수 경향은 지반-드럼 접촉상태 및 과다짐(over compaction)에 기인한 것으로 판단된다. 지반의 강성이 낮은 경우에는 진동다짐 중 지반-드럼 접촉상태가 대부분 양호(continuous contact 혹은 partial uplift)하지만, 지반의 강성이 높은 경우에는 지반-드럼 접촉상태가 불량(double jump 혹은 rocking motion)한 현상이 나타난다(Erdmann et al., 2006). 지반-드럼 접촉상태가 불량하면 다짐에너지가 지반에 제대로 전달되지 못하며(White et al., 2011), 또한 지반의 강성에 관계없이 CMV가 급격하게 변화한다(Caicedo, 2018). 본 연구에서는 지능형 다짐과 관련한 국내외 규정(RVS, 1999; ROAD, 1994; ISSMGE, 2005; FHWA, 2014, KCS 10 20 70, 2021)에 따라 다짐 중 드럼의 가진 주파수 및 진폭을 일정하게 유지했다. 따라서 다짐횟수가 증가해 지반의 강성이 커짐에 따라 지반-드럼 접촉상태가 불량한 현상이 빈번히 유발되었을 것으로 예상된다. 또한 지반에 너무 큰 다짐에너지가 가해질 때 입자파쇄 및 흙의 구조적 파괴가 나타나며 강도가 감소하는 현상을 의미하는 과다짐도 높은 다짐횟수에서의 CMV 감소를 유발했을 것으로 보인다. 초기 다짐횟수에서는 지반-드럼 접촉상태가 대부분 양호하므로 CMV의 평균값이 증가하고 변동계수가 감소하는 경향(즉, 다짐횟수에 따라 다짐 품질이 개선되는 경향)을 보였다. 반면, 특정 수준의 다짐횟수를 넘어서면 지반-드럼 접촉상태가 불량한 현상 및 과다짐이 유발되므로 다짐효과가 감소(CMV 평균값의 증분 감소)하고 CMV의 변동성이 증가(변동계수가 증가)한 것이다. 이상을 종합해 볼 때, 효율적인 다짐을 위해서는 지반의 강성(혹은 다짐도)이 증가함에 따라 드럼의 가진 주파수는 높이고 진폭은 낮추는 방식으로 지반-드럼 접촉상태 불량 및 과다짐을 방지해야 할 것으로 보인다(White et al., 2007).
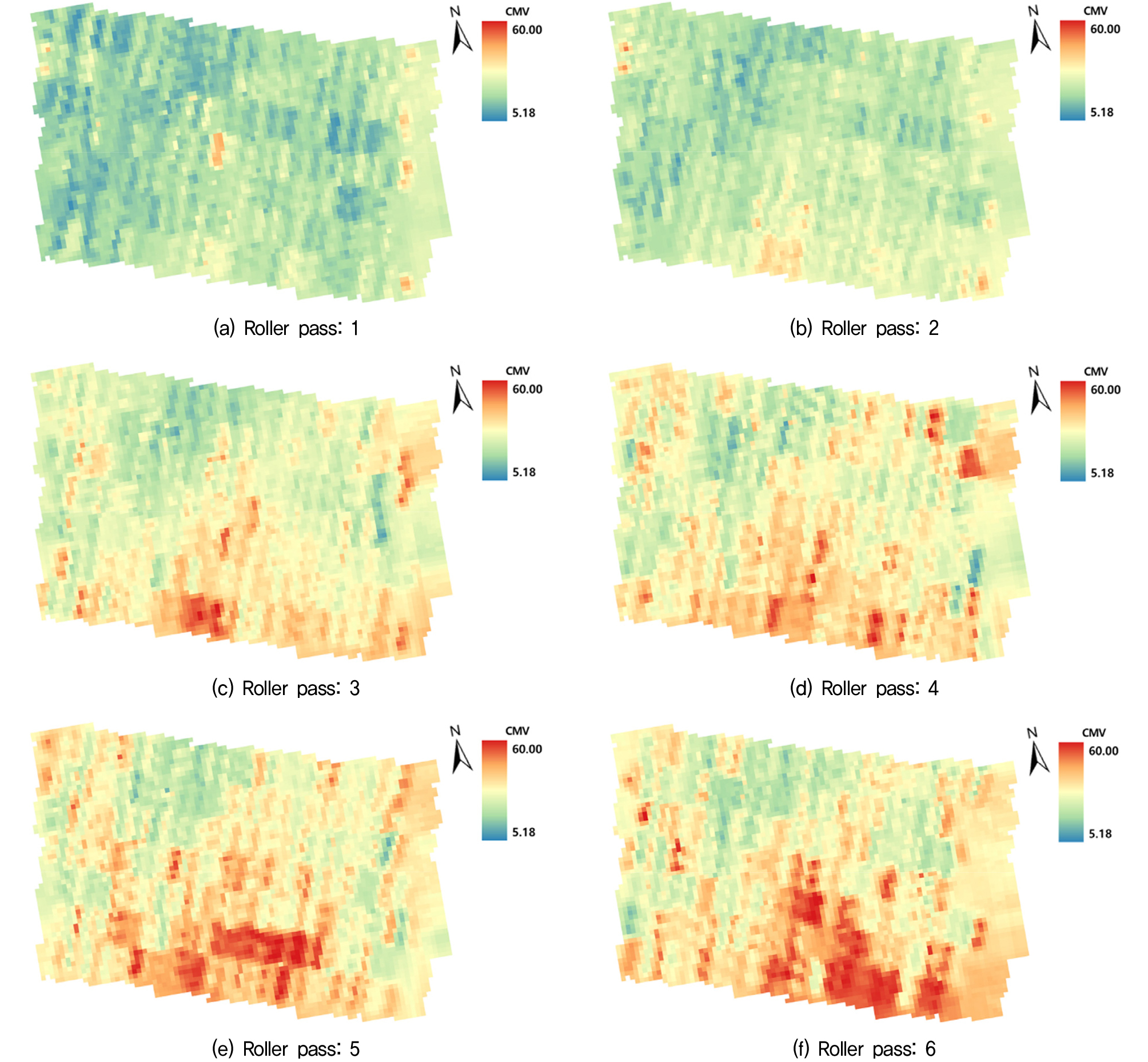
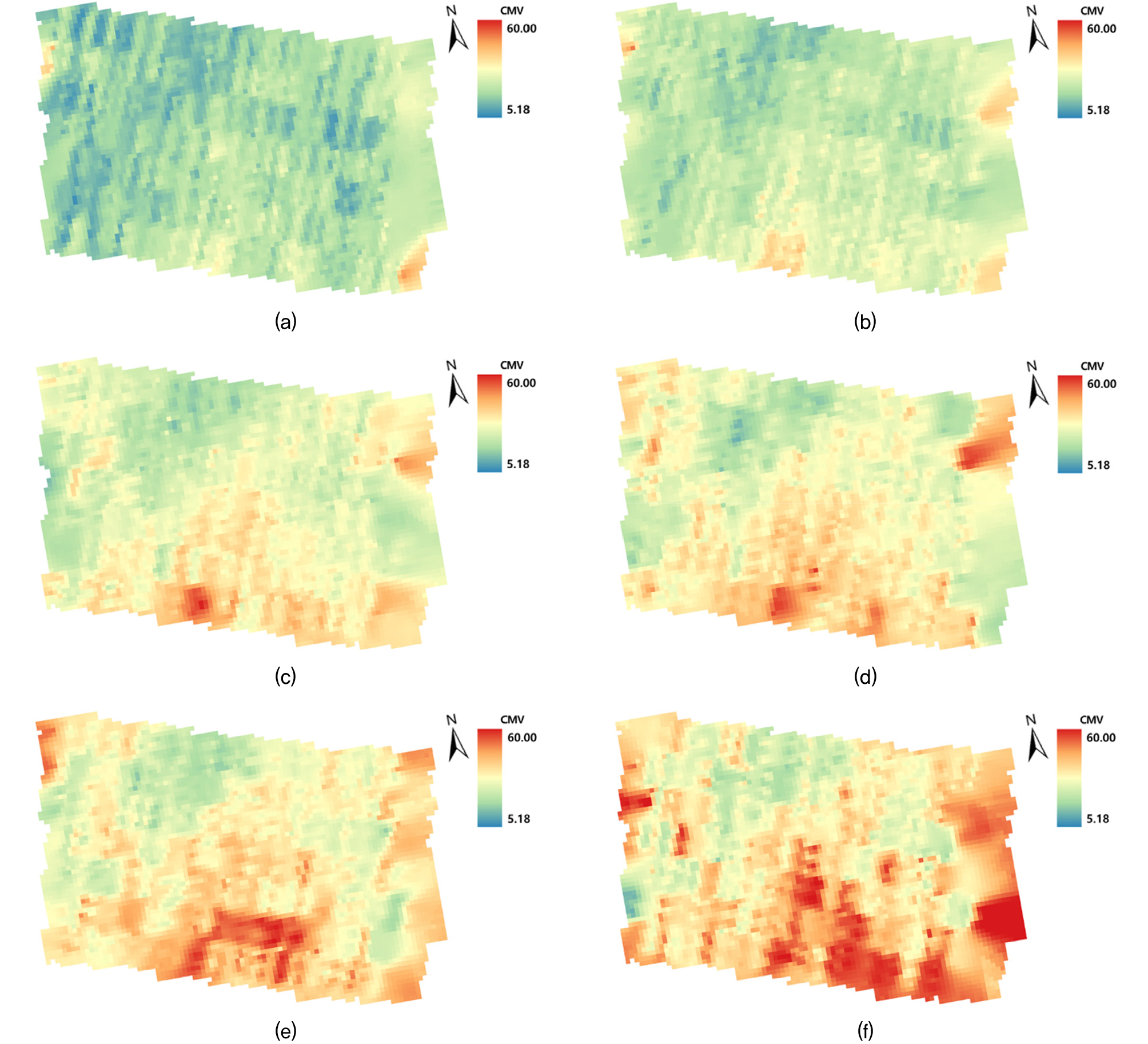
Fig. 7은 ArcGIS 소프트웨어를 통해 정규 크리깅(ordinary kriging)을 수행해 얻은 CMV의 공간분포를 나타낸 것이다. 이때, leave-one-out 방식의 교차검증에 의한 평균 RMSE(Root Mean Square Error) 값은 4.69로 산정되었다. 모든 다짐횟수에 대해 북서쪽에서 측정된 CMV 값이 상대적으로 작고 동남쪽에서 측정된 값이 상대적으로 컸다. 현장조건을 최대한 균질하게 조성하려고 노력했음에도 불구하고, 원지반의 불균질성, 성토재료의 불균질성, 환경조건(함수비 등)의 불균질성 등이 다짐 품질에 영향을 미쳤기 때문으로 보인다. Fig. 6에서 확인한 경향과 마찬가지로, 다짐횟수가 증가함에 따라 특정한 위치에서 측정된 CMV는 점점 커졌지만 위치별 변동성은 크게 개선되지 않았다. 이는 시공영역 전체에 균일한 다짐횟수를 적용하는 종래의 방식으로는 다짐 품질의 변동성을 감소시키기 어렵다는 것을 의미한다. 지능형 다짐값은 시공 중 실시간-연속적으로 도출되므로, 지능형 다짐값을 통해 다짐 중 취약 영역을 실시간으로 확인한 뒤 이곳에 다짐을 집중적으로 실시한다면 보다 균질한 다짐 품질을 획득할 수 있을 것으로 판단된다.
CMV의 공간분포는 대표적인 이상치 분석법들(3-sigma 법칙, boxplot 법칙 등)과 같이 데이터 분포에서 극단적으로 큰 값과 작은 값을 제거하는 방식을 CMV 분석에 적용하는 것이 부적절함을 보여준다. Fig. 7에서 확인할 수 있듯이, CMV는 위치에 따라 매우 크거나 작은값이 나타나며 CMV의 공간분포(즉, 매우 크거나 작은값이 분포한 영역)는 다짐횟수에 관계없이 거의 유사하다. 즉, 매우 크거나 작은 CMV 값이 이상치가 아니라 실제 다짐 품질 정보일 수 있는 것이다. 기존의 대표적 이상치 분석법과 달리, 본 연구에서 제안한 이상치 분석 기법은 CMV의 공간분포를 고려할 수 있다. 제안된 기법에서는 다짐횟수 증가에도 불구하고 특정 위치에서 측정된 CMV가 감소하는 경우를 1차적으로 선별(filtering)하고, 이 중 인접한 위치(유효반경 내)에서 측정된 값들과의 차이가 큰 값들을 이상치로 판별한다(Fig. 1). 이를 통해 지반의 내재적 불균질성은 고려하면서 다짐 품질과 관계없는 다짐롤러 구동조건(속도, 진동수, 진폭, 지반-드럼 접촉상태 등)의 변화에 따른 영향만을 배제할 수 있을 것으로 판단된다.
4.2 CMV 이상치 분석 기법 실증
Table 2는 대표적인 이상치 분석 기법인 3-sigma 법칙, boxplot 법칙과 본 연구에서 제안된 이상치 분석 기법을 적용했을 때의 이상치 제거 비율을 나타낸다. 3-sigma 법칙에서는 평균에서 표준편차(σ)의 1, 2, 3배 만큼 벗어난 데이터를 이상치로 판별(데이터를 정규분포로 가정했을 때, 각각 68.26%, 95.45%, 99.73%의 데이터가 이 범위에 들어가며 그 밖의 데이터를 이상치로 판별)하므로, 동일한 기준을 적용한 경우 다짐횟수에 관계없이 이상치 제거 비율이 거의 비슷했다. Boxplot 법칙은 전체 데이터를 오름차순으로 정렬했을 때의 1사분위 값(Q1)과 3사분위 값(Q3)의 차이인 IQR(Inter Quantile Range)을 이용한다. Q1에서 1.5*IQR을 뺀 값(최소값)보다 작거나 혹은 Q3에서 1.5*IQR을 뺀 값(최대값)보다 큰 데이터를 이상치로 판별했는데, 이상치 제거 비율은 3-sigma 법칙에서 표준편차의 3배(±3σ)를 적용했을 때와 비슷했다.
Table 2.
Outlier removal rate of CMV data by roller passes
반면, 본 연구에서 제안된 이상치 분석 기법의 경우 다짐횟수가 증가할수록 이상치 제거 비율이 점차 증가하는 경향을 보였다. 앞서 언급한 바와 같이 다짐횟수가 증가해 지반의 강성이 커지면 지반-드럼 접촉상태가 불량한 현상이 빈번하게 발생한다. 지반-드럼 접촉상태 불량이 지반 강성에 관계없는 CMV의 변동(fluctuate)을 유발하여 이상치가 많이 나타나는 것이다. 다만, 최종 다짐횟수인 6회의 이상치 비율은 4회와 5회에 비해 낮았는데, 이는 최종 다짐횟수에서 이상치로 매우 큰 CMV 값이 나타난 경우 제거되지 않았기 때문이다(매우 큰 CMV 값을 이상치로 판별하기 위해서는 다음 다짐횟수에서 CMV 값의 감소가 확인되어야 함). 최종 다짐횟수에서 나타나는 매우 큰 CMV 값을 이상치로 판별하기 위해서는 다짐횟수 증가에 따른 CMV 증가율의 상한을 분석하고 이를 이상치 판별 기준으로 활용하기 위한 추가 연구가 필요할 것으로 판단된다.
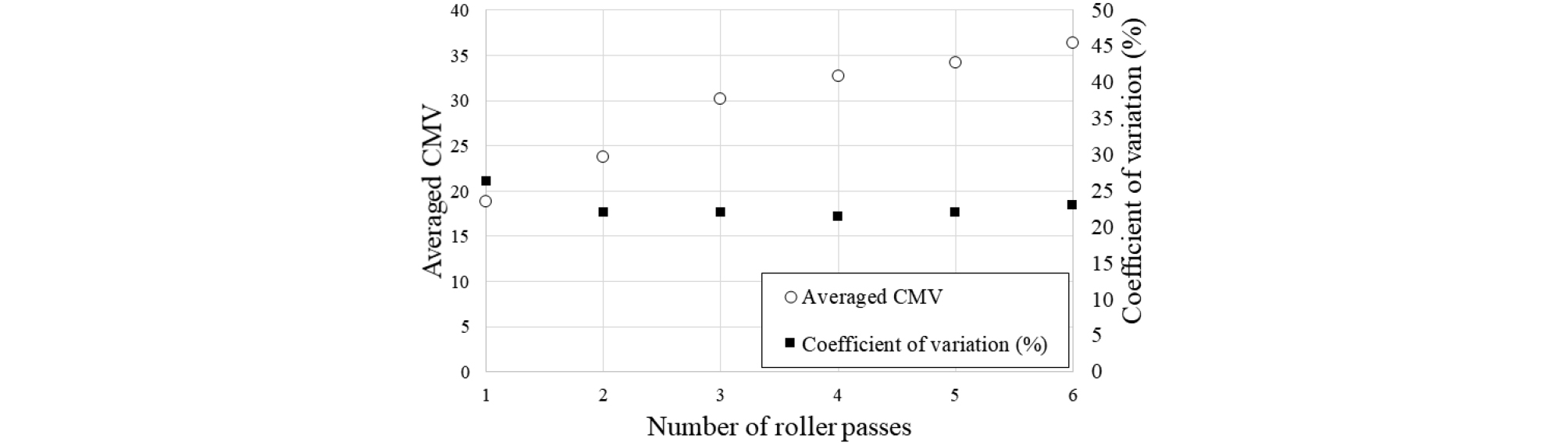
Fig. 8은 본 연구에서 제안된 이상치 분석 기법을 적용해 이상치를 제거한 뒤 얻어진 CMV의 평균값과 변동계수를 다짐횟수에 따라 나타낸 것이다. 다짐횟수가 증가할수록 CMV 평균값(18.9~36.3)은 증가하는 경향을 보였고, 변동계수는 21.4~26.3% 범위에 존재했다. CMV 평균값의 증분은 이상치 제거 전과 비슷하게 다짐횟수 증가에 따라 점차 감소했지만, 다짐횟수 5회와 6회에서 CMV 평균값이 유사한 현상은 발생하지 않았다. 또한 변동계수 크기가 이상치 제거 전(24.7~29.6%)에 비해 감소했고 후기 다짐횟수(4~6회)에서 변동계수가 반등하는 경향이 약화되었다. 이는 후기 다짐횟수에서 지반-드럼 접촉상태가 불량한 상태에서 측정된 CMV 값이 이상치로 판별되어 제거된 결과로, 이상치 분석 기법 적용을 통해 다짐횟수에 따라 다짐 품질이 개선되는 경향(CMV의 평균값이 증가하고 변동계수가 감소하는 경향)을 보다 명확히 확인할 수 있음을 보여준다. 다만, CMV의 변동계수는 RVS(1999)와 ISSMGE(2005)의 지능형 다짐값 변동계수 기준인 20%에 비해 여전히 높은 수준이었다. 본 연구의 현장조건이 실제 시공현장에 비해 매우 엄격히 관리되었음을 고려할 때, 실제 시공현장에서의 변동계수는 본 연구에서 얻어진 값이 비해 높을 것으로 예상된다. Baek et al.(2024a)에서 언급한 바와 같이, RVS(1999)와 ISSMGE(2005)에서 규정하는 변동계수 기준은 너무 엄격하며, 추후 본 연구를 포함한 많은 현장시험 데이터를 바탕으로 합리적인 기준이 제안되어야 할 것으로 판단된다.
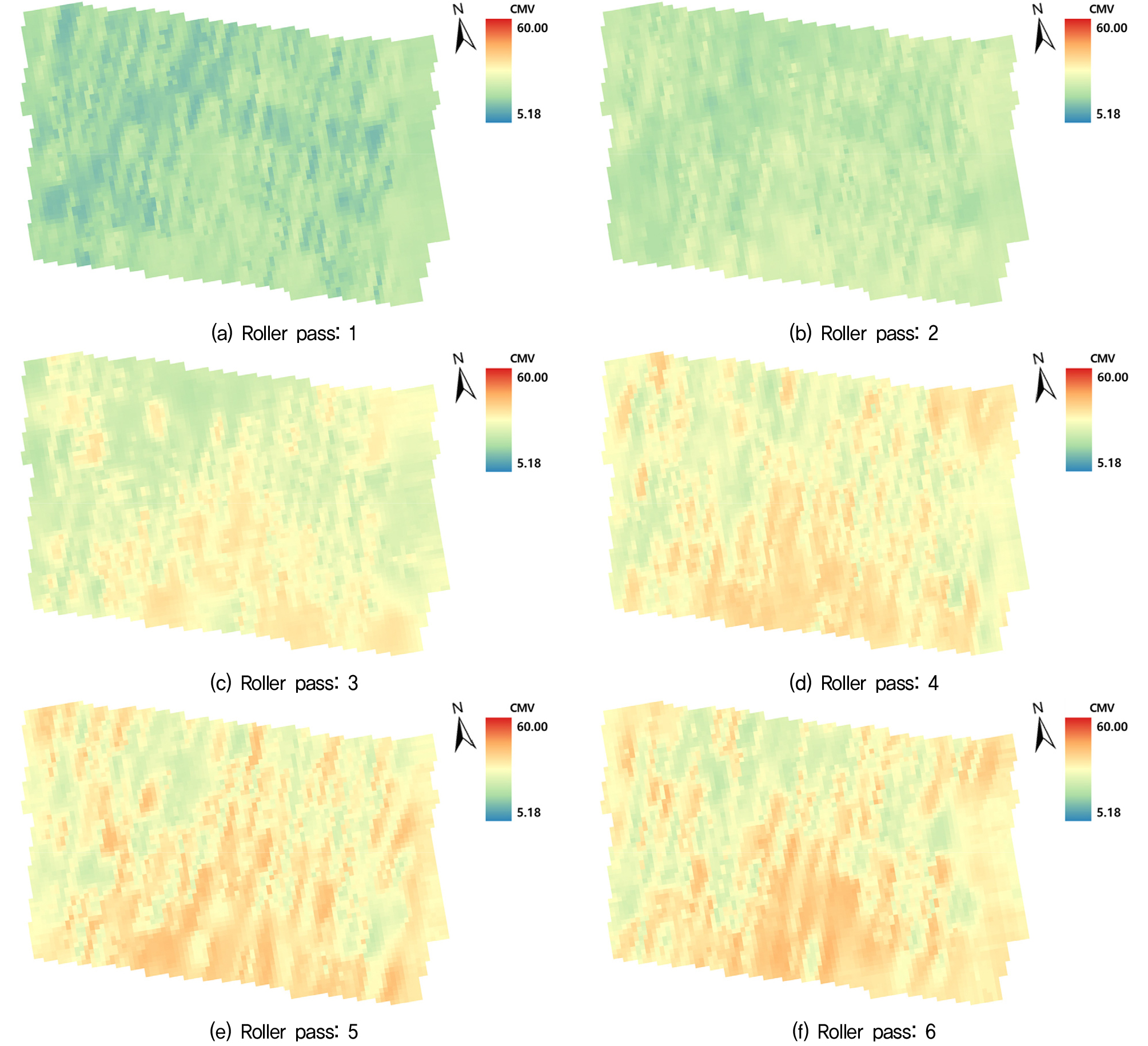
Fig. 9와 10은 각각 3-sigma 법칙(±1σ)과 본 연구에서 제안한 방법을 통해 이상치를 제거한 후 ArcGIS 소프트웨어를 통해 정규 크리깅을 수행해 얻은 CMV의 공간분포이다. 이때, leave-one-out 방식의 교차검증을 통해 산정된 평균 RMSE 값은 각각 3.18과 3.89로 모두 이상치 제거 전(4.69)에 비해 감소했다. Fig. 9에서 확인할 수 있듯이, 극단적으로 큰 값과 작은 값을 제거하는 3-sigma 법칙(±1σ)을 이용해 이상치를 제거하는 경우 다짐 품질의 위치별 변동성을 제대로 고려할 수 없었다. CMV의 공간분포를 고려하지 않고 단순히 매우 크거나 작은 값을 제거했기 때문에 실제에 비해 매우 균질한 다짐 품질 분포도가 나타났다. 반면, 본 연구에서 제안된 방법은 CMV의 공간분포를 고려해 이상치를 제거하므로, 지반의 내재적 불균질성에 따른 다짐 품질의 위치별 변동성은 고려하면서 다짐 품질과 관계없는 다짐롤러 구동조건(속도, 진동수, 진폭, 지반-드럼 접촉상태 등)의 변화에 따른 영향만을 배제할 수 있었다. 특히 두 방법의 이상치 제거 비율(약 30%)이 유사했던 다짐횟수 4회와 5회에서도 그 차이가 명확했는데, 각 방법이 이상치로 판단한 데이터의 공간분포가 완전히 다름을 의미한다. 추후 보다 많은 현장시험 데이터를 바탕으로 제안된 기법의 유효성을 검증하는 과정이 필요하며, 이를 통해 제안된 이상치 분석 기법을 고도화해야 할 것으로 판단된다.
5. 결 론
본 연구에서는 전체 시공영역에 대해 연속적으로 측정되는 지능형 다짐값의 높은 변동성과 관련한 문제를 해결하기 위해서, 지능형 다짐값의 공간적 분포를 고려한 이상치 분석 기법을 제안했다. 지능형 다짐 현장시험을 수행하여 본 연구에서 제안한 이상치 분석 기법을 실증했고, 다음과 같은 결론을 얻었다.
(1) 다짐횟수가 증가할수록 CMV의 평균값과 변동계수가 각각 증가 및 감소하지만, 특정한 다짐횟수 이후에는 CMV 평균값이 거의 증가하지 않고 변동계수가 반등하는 현상이 나타났다. 이는 특정 수준의 다짐횟수를 넘어서면 지반-드럼 접촉상태가 불량한 현상 및 과다짐이 유발되므로 다짐효과가 감소하고 지반의 강성과 관계없는 CMV의 변동이 빈번히 나타나기 때문이다. 따라서, 효율적인 다짐을 위해서는 지반의 강성이 증가함에 따라 드럼의 가진 주파수는 높이고 진폭은 낮추는 방식으로 지반-드럼 접촉상태 불량을 방지해야 할 것으로 보인다.
(2) 다짐횟수가 증가함에 따라 특정한 위치에서 측정된 CMV는 점점 커졌지만 위치별 변동성은 크게 개선되지 않았다. 이는 시공영역 전체에 균일한 다짐횟수를 적용하는 종래의 방식으로는 다짐 품질의 변동성을 감소시키기 어렵다는 것을 의미한다. 지능형 다짐값은 시공 중 실시간-연속적으로 도출되므로, 지능형 다짐값을 통해 다짐 중 취약 영역을 실시간으로 확인한 뒤 집중적으로 다짐한다면 보다 균질한 다짐 품질을 획득할 수 있을 것으로 보인다.
(3) 동일한 다짐횟수라 할지라도 CMV는 위치에 따라 매우 크거나 작은 값이 나타나며 CMV의 공간분포는 다짐횟수에 관계없이 거의 유사했다. 이는 매우 크거나 작은 CMV 값이 이상치가 아니라 실제 다짐 품질 정보일 수 있으며, 기존의 대표적 이상치 분석 기법들과 같이 데이터 분포에서 극단적으로 큰 값과 작은 값을 제거하는 방식으로는 지반의 내재적 불균질성에 따른 다짐 품질의 변동성을 제대로 고려할 수 없음을 의미한다.
(4) CMV의 공간분포를 고려해 새로운 이상치 분석 기법을 제안했다. 제안된 기법에서는 특정 위치에서 측정된 CMV가 다짐횟수 증가에도 불구하고 감소하는 경우를 1차적으로 선별하고, 이 중 유효반경 1.5m 내에서 측정된 값들과의 차이가 큰 값들을 이상치로 판별한다. 현장시험을 통해 측정된 CMV 데이터에 본 연구에서 제안된 이상치 분석 기법을 적용한 결과, 지반의 내재적 불균질성은 고려하면서 다짐 품질과 관계없는 다짐롤러 구동조건의 변화에 따른 영향만을 배제할 수 있는 것으로 나타났다.
상술한 결과가 국내 토공사 현장에서 사용되는 화강풍화토를 사용한 현장시험을 통해 도출된 것임을 고려할 때, 이를 지능형 다짐값 기반 토공사 품질관리를 위한 기초 자료로 활용할 수 있을 것으로 보인다. 특히 이상치 제거 기법을 적용했음에도 CMV의 변동계수가 높은 수준(21.4~26.3%)이라는 점은 지반의 내재적 불균질성에 따라 토공사 품질의 변동성이 높다는 것을 시사한다. 추후 보다 많은 현장시험 데이터를 바탕으로 상술한 결과의 유효성을 검증하는 과정이 필요하며, 이를 통해 제안된 이상치 분석 기법을 고도화하고 지능형 다짐값의 변동성에 대한 합리적인 기준을 제안해야 할 것으로 판단된다.