1. 서 론
국내 지형조건은 산악지역이 70% 이상이며 급경사로 구성되어 지형 여건상 강우로 인한 산사태가 발생할 확률이 매우 높다. 해마다 6∼8월 사이의 장마철 시기에 토석류 붕괴와 얕은 사면의 파괴가 집중적으로 발생하여 재산상 손실과 수많은 인명 피해가 발생되고 있다. 1980년대보다 2002년∼2011년까지 연평균 산사태 발생면적은 779ha로 89년 발생면적인 231ha보다 3.4배 증가하였다. 이처럼 빈번하게 유발되는 산사태를 발생 이전에 비탈면 발생 가능 원인들을 정확히 예측할 수 있다면 경제적·사회적 손실을 줄여 나가는데 크게 도움이 될 것이다. 산사태 위험성 분석은 산사태를 유발시키는 성향으로 정의되어 대상 지역을 확률적으로 표현하기도 하며, 산사태 취약성 지도를 제작하는 방법으로 크게 정성적 해석 기법과 정량적 해석 기법으로 구분하여 분석하기도 한다(Petley, 2004). 산사태 원인을 파악하기 위해서 다양한 방법을 통해 산사태 취약성을 분석하고 그의 타당성을 검증하는 많은 연구가 이루지고 있다(MLTMA, 2011). 우리나라의 경우 한국지질자원연구원이 1998∼2005까지 발생한 10개 지역의 3,485개의 산사태를 분석한 결과 42.3%인 1,452개가 얕은 사면파괴이며 1,452개의 산사태는 얕은 사면파괴와 토석류의 복합된 산사태로 분류되었다. Figs. 1∼2는 국내 대표적인 두 가지 풍화토의 붕괴 현장 모습이다.
국내 산사태의 주요한 발생요인으로는 강우와 그 지반의 특성이다. 비탈면 붕괴를 강우로 인한 포화깊이가 만들어지면서 얕은 파괴로 발생한다고 많은 연구자들의 논문들이 발표되고 있다. 본 연구에서는 불포화 지반을 대상으로 유한요소해석으로 침투해석을 진행하고 강우강도와 강우사상을 변화시키면서 수행한 선행 연구자들의 실내시험과 수치해석의 오류를 확인하고자 2가지 방법을 같은 조건에서 비교하여 검증하고자 한다. 국내에 주를 이루는 비탈면 지반은 편마암풍화토(gneiss weathered soil)와 화강암풍화토(granite weathered soil)로 구분되어 지고 있기 때문에 대표적인 2가지 지반을 대상으로 실내모형 시험을 구성하고 그에 똑같은 조건에서 불포화 침투해석을 실시하여 비교분석하였다. 그에 따른 붕괴가 발생하는 차이점과 그 이유를 파악하고자 한다. 현장에서 발생하는 비탈면 붕괴를 모형시험에서 그 이유를 찾아보려고 하지만 실내시험의 한계를 수치해석을 통하여 원인을 찾아내고, 편마암과 화강암계의 풍화토 차이점을 밝히고자 한다(Kim et al., 2004).
2. 강우침투 실내 모형실험
2.1 실험 조건 및 불포화지반 특성
Figs. 3∼4에서 보여주듯이 비탈면을 조성하여 강우에 의한 침투 실내시험은 한국지질자원연구원에서 진행하였으며, 실제 화강암풍화토와 편마암풍화토의 지반에서 붕괴가 발생한 위치에서 시료를 채취하였다. 연구가 수행된 산사태 모형실험은 충청북도 보은군 지역의 화강암 풍화토와 세종시 장군면 지역의 편마암 풍화토를 사용하였다.
수치해석을 위하여 모형실험에 사용된 토질의 물리적 특성을 실내시험을 통해 얻었으며(KIGAM, 2016), 침투해석에 필요한 함수특성곡선(SWCC, soil water characteristic curve)의 Curve-fitting parameter 역시 실내시험으로 얻어 Table 1에 제시되었다. Table 1에서 제시한 a, n, m은 시료마다 고유한 함수특성곡선을 나타내는 실험계수들이며, AEV/WEV(air entry value/wet entry value)는 포화토에서 불포화토로 변하기 시작하는 공기함입치(AEV)를 나타낸다. 또는 불포화토에서 포화토로 전환되는 시점을 수치적으로 알 수 있는 습윤함입치(WEV)를 나타내는 함수특성곡선에서 확인할 수 있는 모관흡수력(kPa)을 나타낸다. 여기에서 θs는 포화체적함수(saturated volumetric water content), θr는 잔류체적함수비(residual volumetric water content)를 함수특성곡선에서 확인할 수 있다. 화강암풍화토와 편마암풍화토 2가지 시료를 사용하여 각각 2개의 함수특성곡선을 실내시험으로 얻을 수 있었다. 포화토부터 실험을 수행하여 점점 건조시켜 함수특성을 확인하는 함수특성곡선(drying SWCC)과 건조토부터 실험을 수행하여 점점 함수비를 증가시켜 함수특성곡선(wetting SWCC)을 작성하는 방법으로 얻은 결과 값들을 도출하였다. 실내시험 결과와 비교하기 위해서 유한요소해석을 이용한 불포화 침투해석은 일반적으로 많이 쓰이고 있는 SEEP/W(GeoStudio, 2016) 프로그램을 활용하였다(van Genuchten, 1980; Fredlund and Xing, 1994).
Table 1.
Soil water characteristic curve of granite and gneiss weathered soils
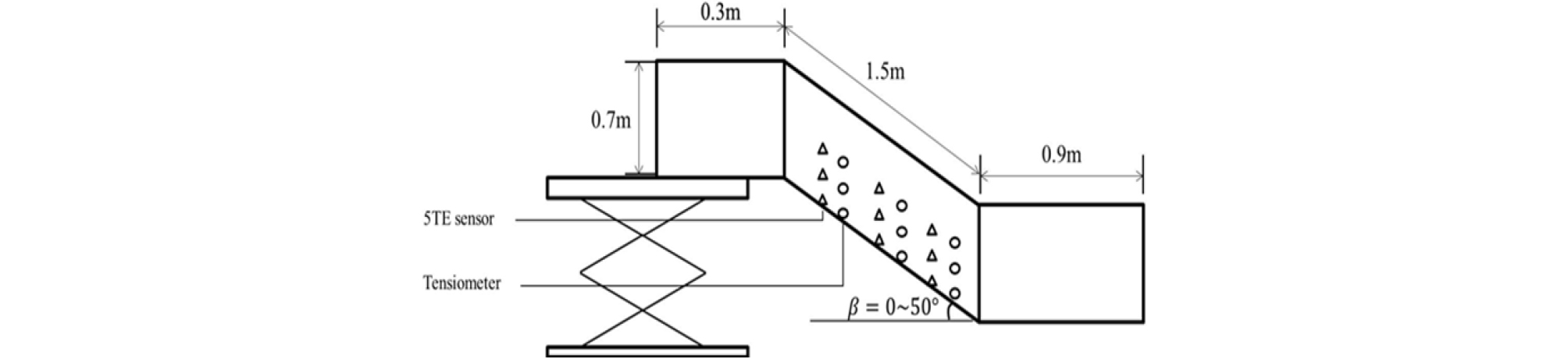
강우 시 지반내의 위험성을 예측하려면 지반의 체적함수비 변화 양상을 알아보기 위하여 TDR 센서를 바닥면을 기준으로 총 9개의 센서를 20cm 간격으로 설치하였다. Fig. 3은 산사태 모형실험장치로 인공강우를 이용하여 TDR 센서에서 체적함수비를 측정하였고, 이때 실내시험의 인공강우는 200mm/hr를 적용시켰다(KIGAM, 2016). 실험실에 설치된 비탈면의 경사는 35도로 구성하였고, 사면의 길이는 1.5m로 조성하였다. 센서들은 비탈면 내부에 체적함수비를 측정하는 센서 9개와 모관흡수력을 측정하는 센서 9개를 3단으로 구성하여 배치하였다.
실내시험에서 수행한 200mm/hr의 강우강도는 극한강우로 파괴를 유도하기 위해서 제시한 조건이므로, 강우를 조성한 이후부터 깊은 세굴이 발생하기 시작하면서 토석류의 발생이 유도되어 전체적인 파괴는 2시간 정도 후에 거의 붕괴되었다. 강우를 조성하기 시작하면서 센서에서는 강우 침투로 발생되는 체적함수비를 측정하여 비교할 수 있었다(Kim, 2002).
2.2 강우침투를 위한 수치해석
실내시험으로 수행된 강우시 비탈면의 안정성 평가는 수치해석으로 검증하기 위해서 불포화 침투해석을 실시하였다. 사면이 조성된 전체높이는 1.35m이며, 비탈면 경사각은 35°를 이루는 사면으로 mesh를 Fig. 5와 같이 구성하였다. 초기에는 실내시험과 같은 강우인 200mm/hr로 입력을 하여 수행한 결과 지반 내의 체적함수비는 너무 큰 차이로 모형실험과 수치해석의 결과의 차이를 보였다. 그 이유로 모형토조 실험에서 실질적인 강우를 적용하여 모든 강우량이 침투되어 지반내로 스며드는 것은 아니다. 강우를 뿌리고 비탈면 지표위로 흐르는 물들이 상당수를 포함한다. 그래서 불포화 지반의 침투해석에서는 강우강도를 줄여가면서 실제 모형토조 실험에서 얻은 지반내의 체적함수비의 값과 비교하여 강우가 침투된 물의 양을 분석하기로 하였다.
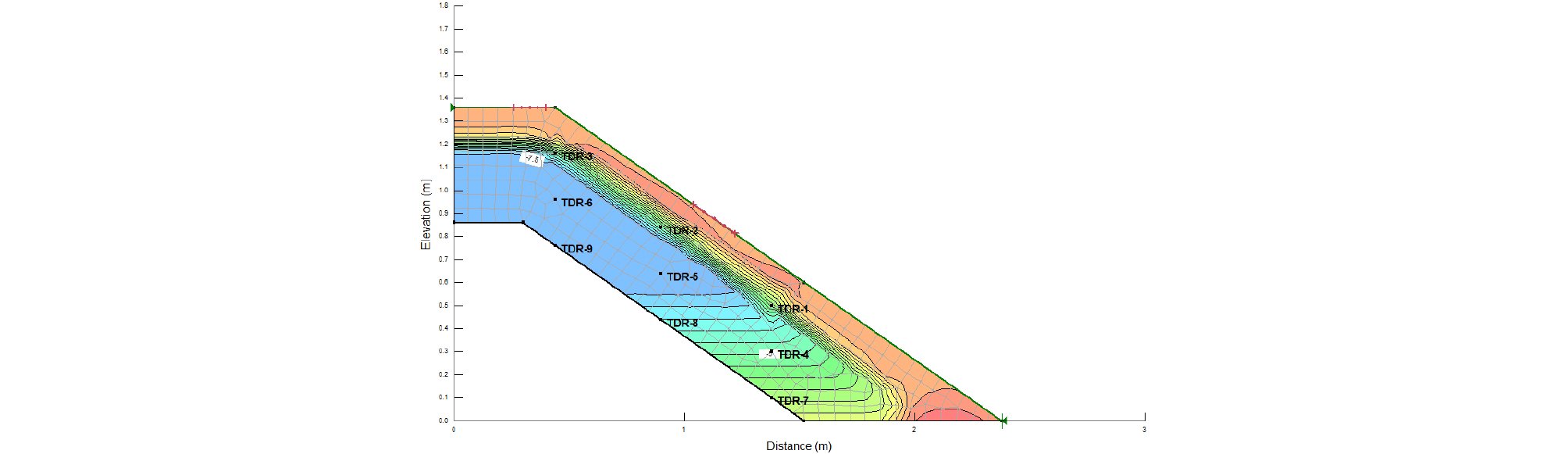
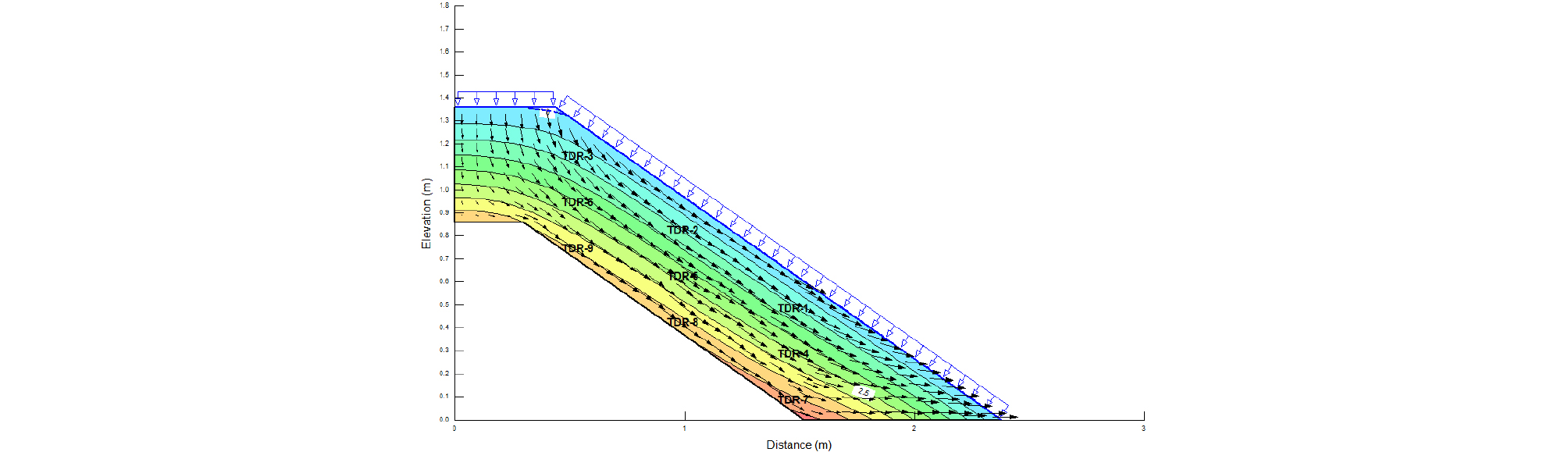
간단한 지형조건으로 비탈면 침투해석 시 체적함수비를 측정(Fig. 5)하기 위해 센서들의 위치들을 보여주고 있다. Fig. 6은 수치해석 결과로서 강우가 침투되어 표층부터 포화되는 간극수압 분포를 보여주고 있다. 본 논문에서는 깊이별 3층으로 이루어진 각각의 3개의 센서들에서 얻은 체적함수비 측정값들을 모형토조 실험과 수치해석에서 얻은 값을 비교하여 분석하였다. 프로그램으로 수행한 불포화 지반의 침투해석에서는 강우조건을 입력하면 입력된 강우가 투수계수의 크기만큼 모두 침투되어서 결과 값들을 볼 수 있기 때문에 모형토조에서 발생하는 지표면 위로 흐르는 강우들을 고려하지 못한다. 따라서, 수치해석에서 강우강도를 감소시켜 실제 모형토조 실험에서 적용시킨 강우에서 얼마나 침투되었는지 역으로 계산할 수 있다.
3. 실내실험과 수치해석의 비교
비탈면의 붕괴를 확인하고자 실내시험에서는 모형강우를 조성하여 200mm/hr의 극한강우로 사면파괴를 유도하였다. 시간이 경과됨에 따라 표면이 침식되어 시간이 경과됨에 따라 점차적으로 붕괴가 진행되고 있었으나, 한계평형해석에서 주로 얻는 원호파괴단면은 확인할 수 없었다. 실내실험과 수치해석에서 비교할 수 있는 결과들 중에 제일 분명한 것은 지반 내로 침투하는 함수비의 변화를 비교하는 것이다. 수치해석에서 적용하는 강우사상은 포화투수계수가 허용하는 범위 내에서는 모든 강우가 침투되어 지반 내의 유효응력을 감소시켜 붕괴를 유발하도록 수치해석은 진행된다(Kim and Kim, 2011; Lu et al., 2010; Lu, 2006; Nuth and Laloui, 2007). 따라서 실내모형시험에서 적용한 강우강도 200mm/hr가 모두 침투되어 지반 내에 체적함수비가 측정이 되었는지 확인하고자 수치해석과 실내모형시험의 지반 내 체적함수비를 비교해 보았다(Ng and Pang, 2000).
실내모형시험에서 체적함수비를 측정하기 위해서 설치한 센서들의 위치들은 비탈면의 바닥면을 기준으로 20cm 수직 간격으로 되어 있다. 표층에 가까운 센서를 1단, 중간이 2단, 그리고 사면의 바닥면에 위치한 센서들을 3단으로 지정하고 각각의 센서에서 얻은 결과들을 수치해석에서와 같은 경계조건으로 비교하였다.
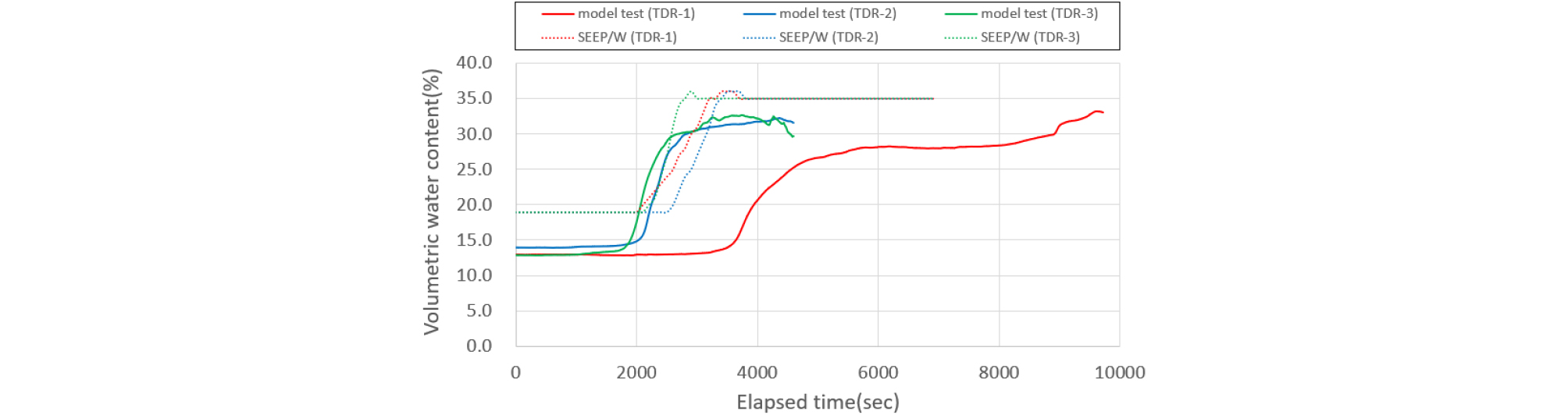
각 그래프들은 최종 강우시간인 10,000 sec를 가로축으로 체적함수비 변화를 세로축으로 경향을 비교하였다. 실내시험에서 적용한 200mm/hr 강우강도에서의 체적함수비는 수치해석에서도 같은 강우강도(200mm/hr)에서 얻은 체적함수비와는 많은 차이를 보였다. 수치해석에서 적용한 강우강도를 점차적으로 줄여서 실내시험에서 얻은 체적함수비와 비슷한 경향을 갖게하는 강우강도는 화강암풍화토에서 40mm/hr 강우강도이다.
Figs. 7∼8에서와 같이 200mm/hr 강우강도에서 1단 센서에서 33분(2,000 sec)정도가 지나면서 수치해석 결과는 체적함수비가 변화가 시작하는걸 알 수 있다. 그러나 40mm/hr로 강우강도를 감소하여 해석한다면 Fig. 8 그래프와 같이 40분(2,800 sec)정도가 경과할 때 체적함수비 변화가 시작되고 있다. Fig. 9∼10에서와 같이 200mm/hr 강우강도에서 2단 센서에서 1시간 10분(4,100 sec)정도가 지나면서 수치해석 결과는 체적함수비가 변화가 시작하는걸 알 수 있다. 그러나 40mm/hr로 강우강도를 감소하여 해석한다면 Fig. 10와 같이 1시간 30분(5,000 sec)정도가 경과할 때 체적함수비 변화가 시작되고 있다.
3단 센서에서도 마찬가지로 Figs. 11∼12에서 200mm/hr 강우강도에서 3단 센서에서 1시간 40분(6,000sec)정도가 지나면서 수치해석 결과는 체적함수비 변화가 시작되고 있다. 그러나 40mm/hr로 강우강도를 감소하여 해석한다면 Fig. 12와 같이 2시간 10분(8,000sec)정도가 경과할 때 체적함수비 변화가 다르게 시작되고 있다.
따라서 Figs. 7∼12에서 보여준 화강암풍화토 비탈면에서의 체적함수비 변화는 초기 지반 내 강우침투량 차이로 극한강우(200mm/hr)에서 실내시험과 수치해석의 침투 진행이 차이를 많이 보이고 있었다. 실내시험과 수치해석의 비슷한 침투결과를 보이는 강우는 40mm/hr 였으며, 현장 비탈면에서 실제 강우는 초기에 많은 강우가 침투하지 못하고 표층으로 흐르며 포화층이 형성되기 위해서는 표층이 충분히 젖는 시간이 필요한 것으로 판단된다.
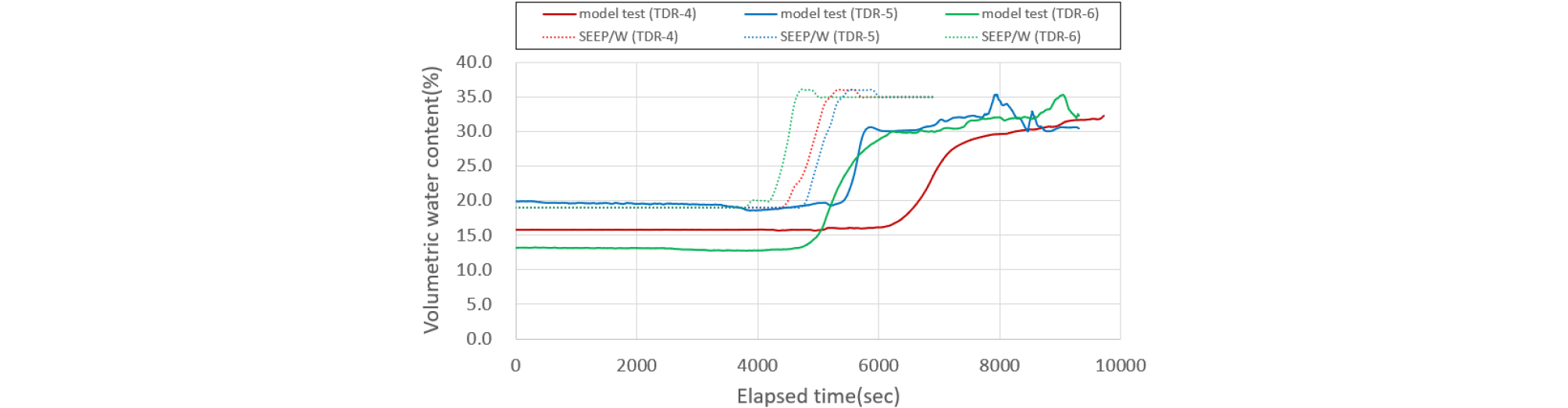
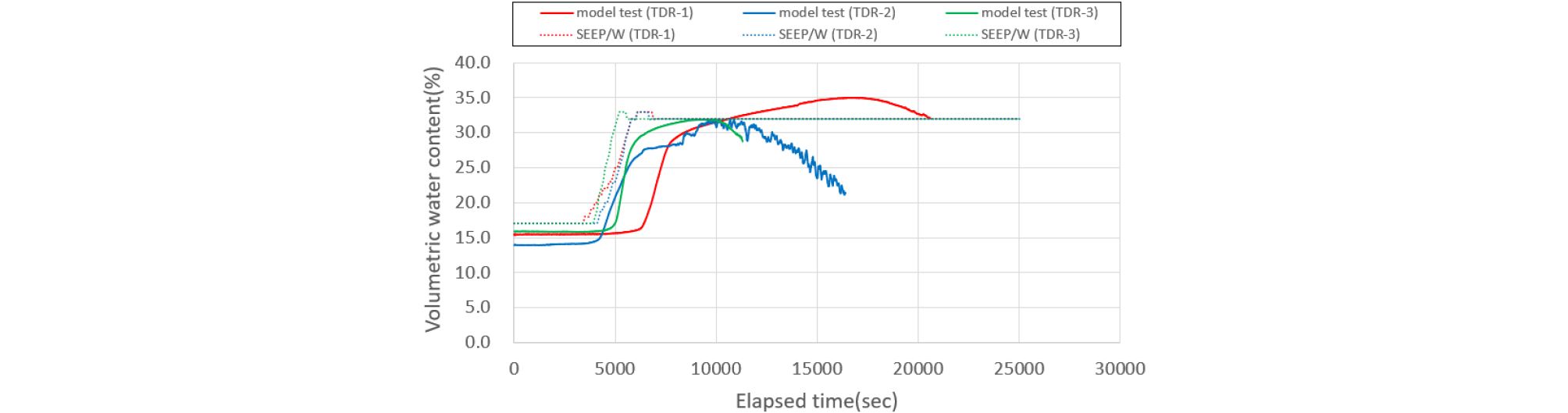
같은 강우와 비탈면의 불안정성을 확인하기 위해서 편마암풍화토를 대상으로 비교분석을 하였다. 편마암풍화토는 화강암풍화토보다 세립토가 많이 함유하고 있기 때문에 비탈면 표층에서 침투하는 속도가 느렸으며, 시간이 경과함에 따라 침식으로 인한 사면 파괴 역시 비교적 많은 시간이 필요함을 확인하였다. Figs. 13∼18은 편마암풍화토 지반을 대상으로 실내모형시험과 수치해석의 결과를 비교한 것이다. 화강암풍화토 비탈면 비교에서와 마찬가지로 Figs. 13∼14에서 200mm/hr 강우강도를 적용할 때 1단 센서 결과를 보여준다. 이 모형토조 실험에서는 1시간 6분(4,000 sec)이 지나서 첫 번째 반응을 보이기 시작하였지만, 수치해석은 초기부터 강우 침투가 시작하므로 1시간(3,600 sec)정도 경과될 때 체적함수비 증가가 시작되었다.
화강암풍화토에서 같은 강우강도로 반응했던 체적함수비는 편마암풍화토 지반에서 2배 이상 느린 반응을 보여주고 있다. 화강암풍화토 지반 내 1단 센서 반응은 1,800 sec에서 첫 체적함수비 반응을 보였으나, 편마암풍화토 지반에서는 비교적 늦은 3,600 sec에서 반응을 보이고 있었다.
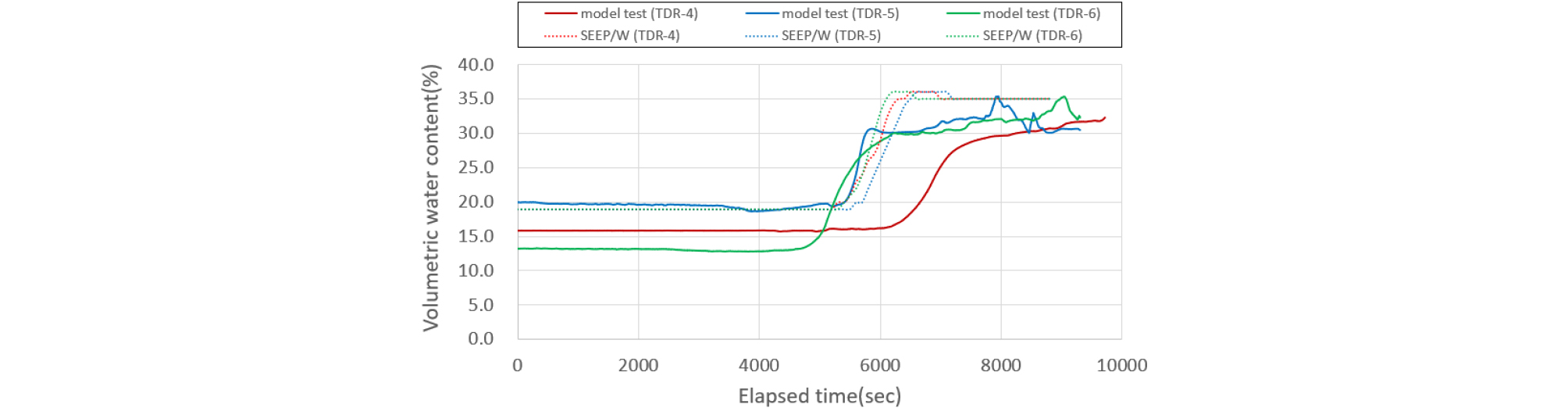
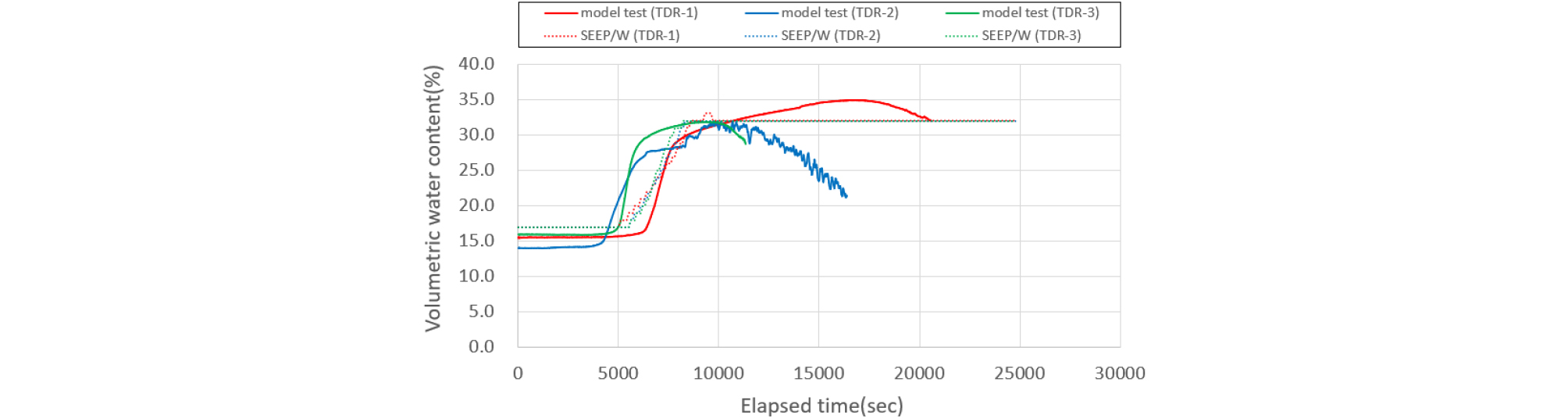
Figs. 15∼16에서와 같이 200mm/hr 강우강도를 적용할 때 2단 센서에서의 모형토조 실험에서는 3시간(11,000 sec)이 지나서 첫 번째 반응을 보이기 시작하였지만, 수치해석은 많은 강우의 침투로 대략 2시간 10분(8,000 sec)정도 경과될 때 체적함수비 증가를 보이기 시작했다. 200mm/hr 강우강도를 적용하여 침투한 체적함수비의 실내시험 결과는 수치해석에서 13mm/hr 강우강도를 적용하여 검토한 지반 내의 체적함수비 변화와 거의 비슷한 경향을 Fig. 16에서 보여주고 있다. 비탈면의 2단 센서 위치들이 높이별로 3가지로 구분되어 측정된 체적함수비 변화 시간이 약간 차이를 보여주고 있으나 대체적으로 화강암풍화토 지반일 경우보다 많은 늦춰지고 있음을 알 수 있다.
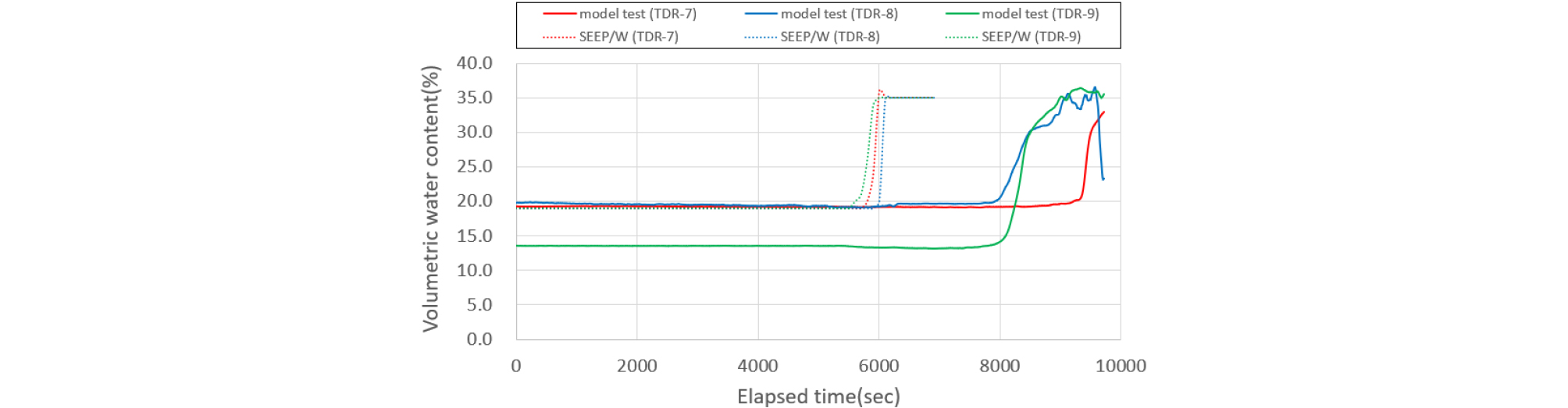
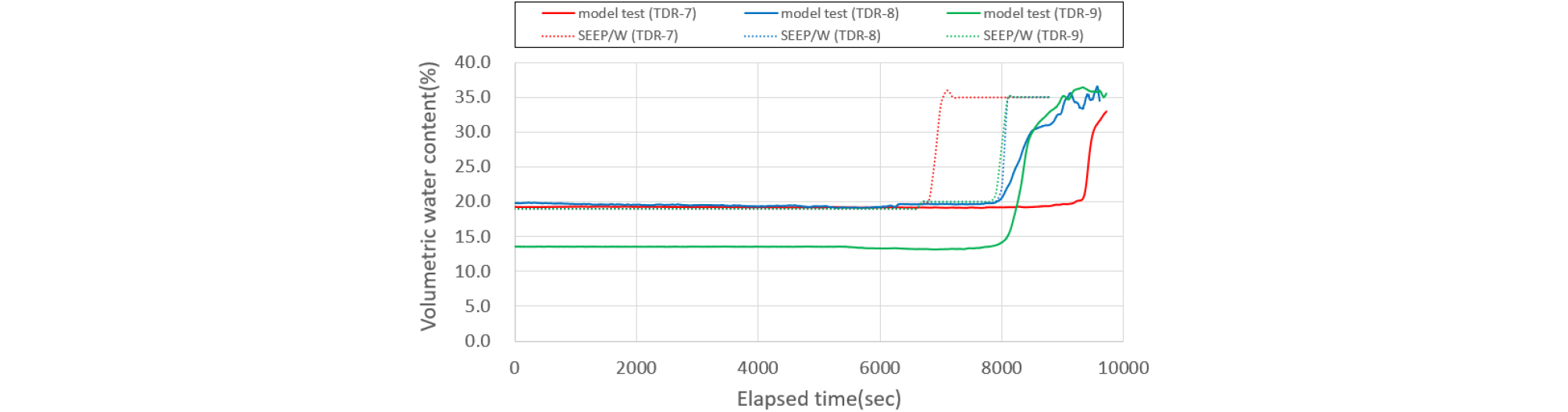
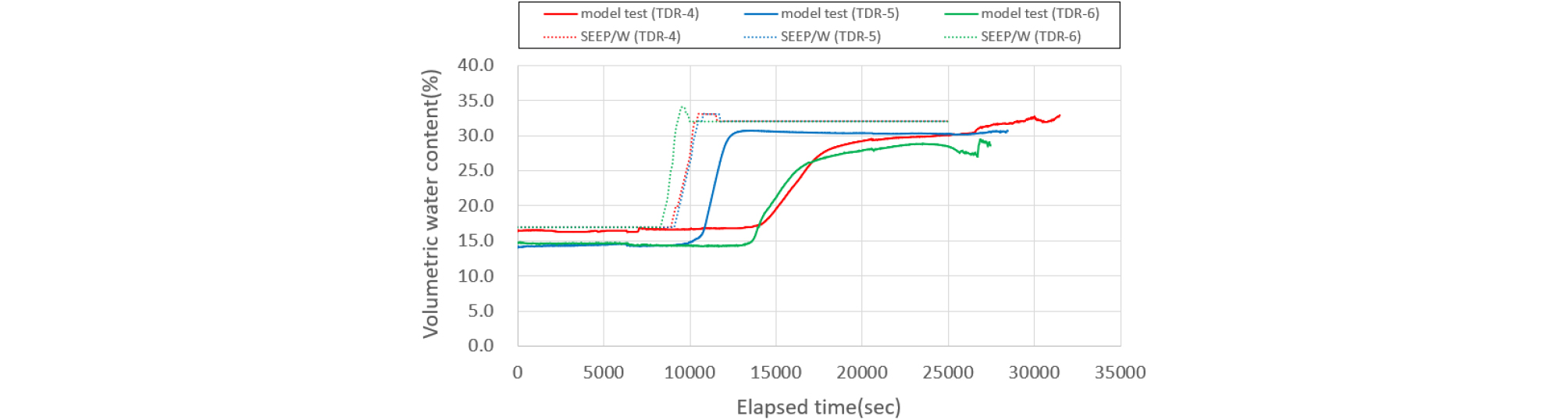
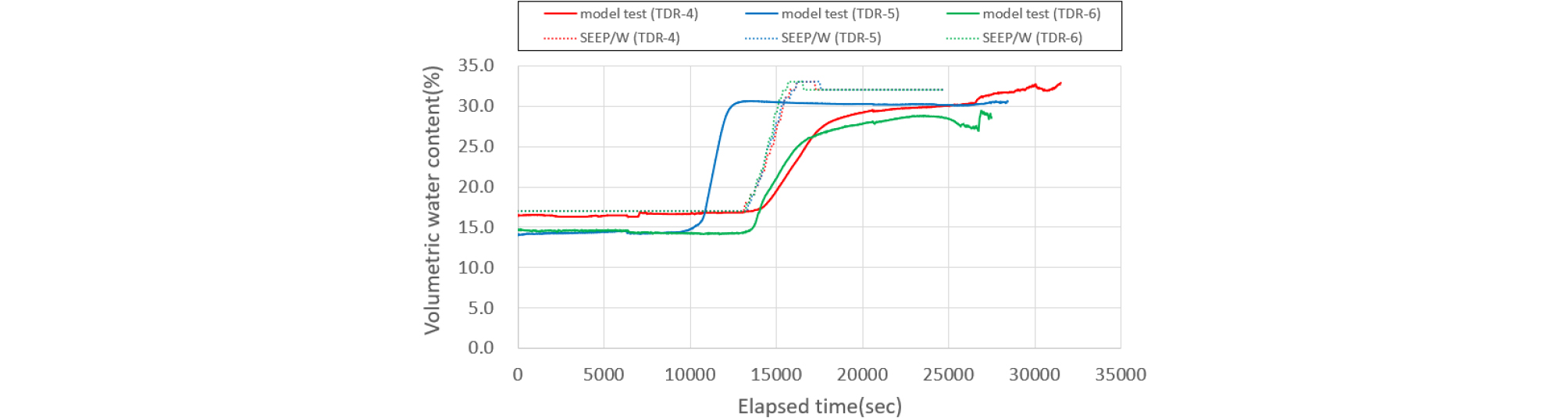
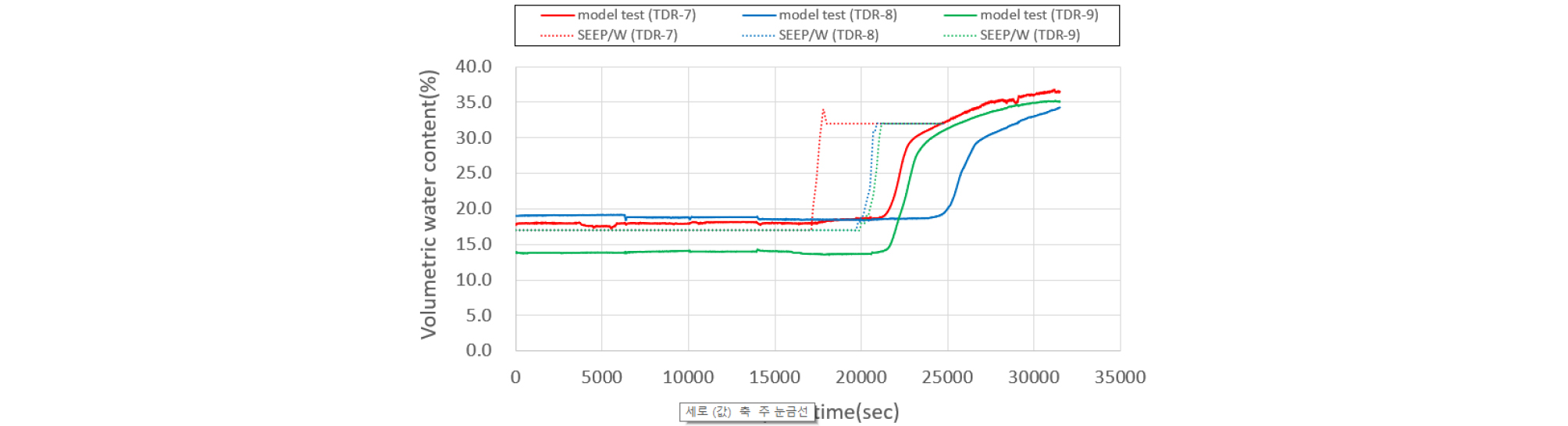
실내모형실험의 체적함수비 반응은 위치별로 간격을 두고 변화하지만 수치해석은 3가지 모든 센서에서 같은 반응을 보여준다. 그러나 실내시험으로 얻은 체적함수비 변화량은 각 센서위치마다 조금씩 차이를 보이기 때문에 평균값들을 사용하여 침투량을 결정하였다. 특히, 편마암풍화토 지반에서 3단 센서의 변화량을 비교하였을 때, Figs. 17∼18에서와 같이 200mm/hr 강우강도를 적용 시, 3단 센서에서의 모형토조 실험에서는 3가지 센서 중 6시간(22,000 sec)이 지나서 첫 번째 반응을 보이기 시작하였고, 마지막 반응은 대략 7시간(25,000sec)이 지나 최종적인 침투량을 확인할 수 있었다. 같은 강우강도 200mm/hr를 적용한 수치해석는 투수계수만큼의 강우가 초기부터 침투가 시작하기 때문에 3가지 모든 센서 위치에서 3시간 10분(12,000 sec)정도 경과될 때 체적함수비 증가를 보이기 시작했다. 실내모형실험의 결과와 수치해석을 체적함수비 반응은 거의 2배의 차이를 보여줬다.
강우강도의 크기에 따라서 수치해석과 실내모형시험에서의 침투 반응이 서로 다르지만, 편마암풍화토에서 두 조건이 모두 실제 침투량이 같아지는 강우강도는 200mm/hr의 6.5%에 해당하는 13mm/hr의 강우강도를 적용하였을 때 비슷한 체적함수비 변화 그래프를 보여줬다. 1∼3번의 센서에서 확인되듯이 편마암풍화토에서는 13mm/hr 강우강도를 적용할 때 제일 근접하게 수치해석과 실내모형시험의 체적함수비 변화 경향이 비슷하다는 것을 확인할 수 있다.
이러한 강우강도로 인한 침투량 변화는 비탈면 표층을 포화시키는 시간과 관련이 있기 때문에 사면안정성 해석에 주된 영향을 끼친다. 본 연구에서 강우로 인한 침투시간과 함수비 변화에 대한 오차는 실내시험의 비탈면 지반 다짐도나 입도분포에 따라서 매번 다르게 나타날 것이다. 평균적인 값들을 비교하였을 때 다소 작은 20mm/hr 또는 13mm/hr 강우강도를 수치해석에 적용하면 실제 비탈면에서 침투되어 포화되는 조건들이 비슷하게 모사할 수 있으리라 판단된다. 그러나 200mm/hr와 같은 극한강우로 비탈면의 위험성에 대해서 많은 수치해석이 이루어지고 있다. 이러한 결과들을 제시하는 문헌들의 내용은 실제로 현장에서 벌어지는 상황들과는 차이가 발생한다는 것을 보여주고 있다. 극한강우에서 수치해석은 빠르게 침투가 되어 포화가 발생하거나 더 위험한 붕괴를 야기할 수 있는 결과를 보여줄 수 있다는 것이다.
본 연구에서 실내모형시험에서 적용하는 극한강우는 대부분 표면 지표수로 흘러내리는 유량이 대부분 확인되었으며, 수치해석의 침투유량은 종류에 따라 실제 지반에서 20% 또는 6.5% 정도에 미치지 않았다. 실제 비탈면에서 발생하는 현상들을 유사하게 예측하려면 수치해석에 적용하는 강우강도도 비슷하게 지표를 따라 흘러내리는 경계조건을 입력해야 할 것이다. 일반적으로 수치해석에서는 포화투수계수 결정에 따라 침투유량이 대부분 결정된다. 포화투수계수보다 큰 강우강도 조건에서는 지표면 상부로 강우가 ponding 효과를 고려하여 해석에 다르게 분석할 필요가 있다.
4. 결 론
본 연구에서는 강우 시 화강암 및 편마암 풍화토에서의 산사태 발생 특성을 분석하기 위하여 수치해석을 실시하였으며, 유사 모형실험 결과와 비교·분석하였다. 모형실험 및 수치해석 결과에서 강우가 진행됨에 따라 포화대와 불포화대의 경계가 발생하여 비탈면 위험성을 예측할 수 있었다. 또한 강우강도에 따라 지반의 포화시점이 다소 차이는 있지만 체적함수비 센서를 통하여 수치해석과 실제 비탈면에서 발생하는 유사점과 차이점을 구분할 수 있었으며 다음과 같이 요약할 수 있다.
(1) 실내 모형토조 강우는 초기부터 침투가 발생하지 않고 습윤대 형성 시간이 필요하기 때문에 수치해석보다 느리게 표층 포화대가 형성된다. 수치해석은 초기 강우부터 바로 스며들어 표층 체적함수비가 빨리 증가하여 붕괴 위험성이 현장보다 빠르게 진행된다. 그러나 실제 현장에서는 강우강도로 표층 침식을 야기시켜 토석류 발생의 불안전성을 예측할 수 있었다.
(2) 극한강우조건(200mm/hr)에서는 많은 강우침투가 실제 현장에서 초기에 발생하지 않기 때문에 수치해석보다 느리게 붕괴 위험성을 보여준다. 따라서 수치해석에 의한 시간별 안정성 예측은 현장 사면의 불안정성을 조금 빠른 시각에서 예측한다는 것을 알 수 있다.
(3) 수치해석으로 얻은 결과는 화강암풍화토에서 강우강도 40mm/hr가 적용하였을 때와 세립분이 많이 포함된 편마암 풍화토에서는 강우강도 13mm/hr 적용되었을 때, 모형토조실험에서 적용한 강우 침투량과 유사한 시간에 체적함수비 변화 경향이 관측되었다.
(4) 세립분이 비교적 많은 편마암풍화토의 투수계수(8.03×10-4cm/sec)가 화강암 풍화토(1.89×10-3cm/sec)의 투수계수보다 약 2배 정도 작은 값을 갖기 때문에 침투가 느리게 진행된다. 수치해석과 실내시험의 침투 경향이 비슷한 강우강도를 적용 시, 습윤면적을 비교할 때 강우 침투량도 대략 14% 수치해석보다 실내시험 조건에서 작게 침투가 진행되고 있음을 알 수 있었다.