1. 서 론
2022년 태풍 힌남노로 인하여 포항시 인근에서 여러 군데에 산사태가 발생하였다. 태풍 및 집중강우로 인하여 자연 비탈면에 붕괴가 일어나는 현상은 국내 산사태의 전형적인 사례에 해당한다. 자연 산지는 지형이 높고 토사층이 지하수위 상부에 존재하여, 강우시 지표로부터 불포화층을 통하여 침투가 일어난다. 간극수는 시간이 지남에 따라서 하부로 이동하며, 지층의 포화도가 증가한다. 포화도가 증가하면 모관흡수력이 감소하고 불포화토의 유효응력이 감소한다. 이로 인하여 전단강도는 감소하고 안정성이 저하되는 과정을 겪는다. 아직 지층이 완전하게 포화되기 이전이며 간극수압이 0보다 작은 상태에서도 비탈면은 붕괴하고 산사태가 발생할 수 있다(Lee et al., 2013). 이러한 과정을 시뮬레이션하기 위해서는 불포화토 유효응력에 기반한 수리-역학적 해석이 필요하다(Lu and Likos, 2006; Oh et al., 2012; Lu et al., 2013; Oh et al., 2013).
이러한 수리-역학적 해석은 침투해석과 안정해석으로 이루어진다. 침투해석시에는 불포화토의 함수특성곡선 및 수리전도도 함수가 핵심적인 물성이다. 불포화 수리전도도는 실험적으로 구하는 것이 좋지만 측정하기 까다로워서 간접적인 방법으로 산정하는 것이 일반적이다. 가장 많이 사용하는 Mualem 모델(1976)은 불포화상태의 상대 수리전도도 함수를 함수특성곡선(예를 들어, van Genuchten, 1980)으로부터 추정한다. 그리고 포화시 수리전도도를 이용하여 전체 수리전도도의 크기를 결정한다.
이러한 과정에서는 함수특성곡선의 형태가 불포화 수리전도도 함수의 정확도를 지배할 수 있다. Dunner(1994)에 의하면 입도분포가 한 가지 입경에 집중된 균질한 사질토의 경우에는 단일한 함수특성곡선이 적절할 수 있다. 하지만 균질하지 않은 토질에는 두 개 이상의 결합한 함수특성곡선에 대한 다중함수를 제안하였다. 포항지역의 독특한 지질 특성으로 인하여 시료는 팽창성을 뚜렷하게 보였다. 이로 인하여 함수특성곡선이 팽창 전과 후에 변동이 일어나게 된다. 이 경우에 모두 단일한 모델을 이용하여 수리특성을 표현하기 어렵다. 따라서 van Genuchten 모델에 대한 이중함수에 의한 함수특성곡선을 적용할 수 있다.
본 연구에서는 실제 산사태 피해 현장에서 불교란시료와 교란시료를 채취하였고 증발법 시험을 통하여 함수특성을 측정하였다. 본 연구에서는 불교란 시료를 통하여 팽창 후 수리거동을 획득하고 교란시료를 재성형하여 팽창 전 거동을 획득하였다. 그리고 이를 토대로 산사태가 발생한 지역을 대상으로 2차원 침투해석 및 안정해석을 수행하였고 해석결과를 비교하였다.
2. 산사태 지역의 수리-역학적 물성 평가
불포화 토질역학에서 함수특성곡선(soil water retention curve, SWRC)은 수리-역학적 물성을 평가시 핵심적인 역할을 한다. van Genuchten(1980)은 함수특성곡선을 유효포화도와 모관흡수력의 관계로 식 (1)과 같이 제안하였다.
여기서, Θ는 유효포화도, θs는 포화 체적함수비, θr는 잔류 체적함수비, ψ는 모관흡수력, α는 공기함입치 역수, n은 기울기 관련 계수(m=1-1/n)이다.
Mualem(1976)은 van Genuchten 모델의 함수특성곡선의 함수를 이용하여 불포화토의 투수계수를 식 (2)와 같이 유도하였다.
여기서, K은 투수계수 함수, l은 간극연결성 계수이다(실험적으로 구하는 계수이지만 0.5로 가정함). 불포화 투수계수는 포화투수계수 Ks와 포화도의 함수로 구할 수 있다.
van Genuchten 모델(van Genuchten et al., 1991)을 사용하여 흙의 함수특성시험시 나타나는 거동을 대체로 잘 표현할 수 있다. 하지만 하나의 곡선으로 복잡한 함수특성을 표현하는데 어려울 경우가 있다. Dunner(1994)는 이러한 흙의 함수특성을 예측하기 위하여 두 개 이상의 van Genuchten 모델을 결합한 다중함수를 제안하였다. 단일한 van Genuchten 모델(SVG)을 이중으로 결합한 dual van Genuchten(DVG) 모델로 함수특성곡선을 식 (3)과 같이 나타낼 수 있다.
여기서, wi는 i번째 곡선의 가중치(i=1, 2), αi, ni 그리고 mi은 i번째 곡선에 대한 식 (1)의 van Genuchten 모델 계수들이다.
Dunner는 식 (2)의 van Genuchten-Mualem(VGM) 모델의 투수계수를 이용하여 이중 함수를 결합한 불포화 투수계수를 식 (4)와 같이 정의하였다.
여기서, fi는 i번째 식 (2b) 함수이다.
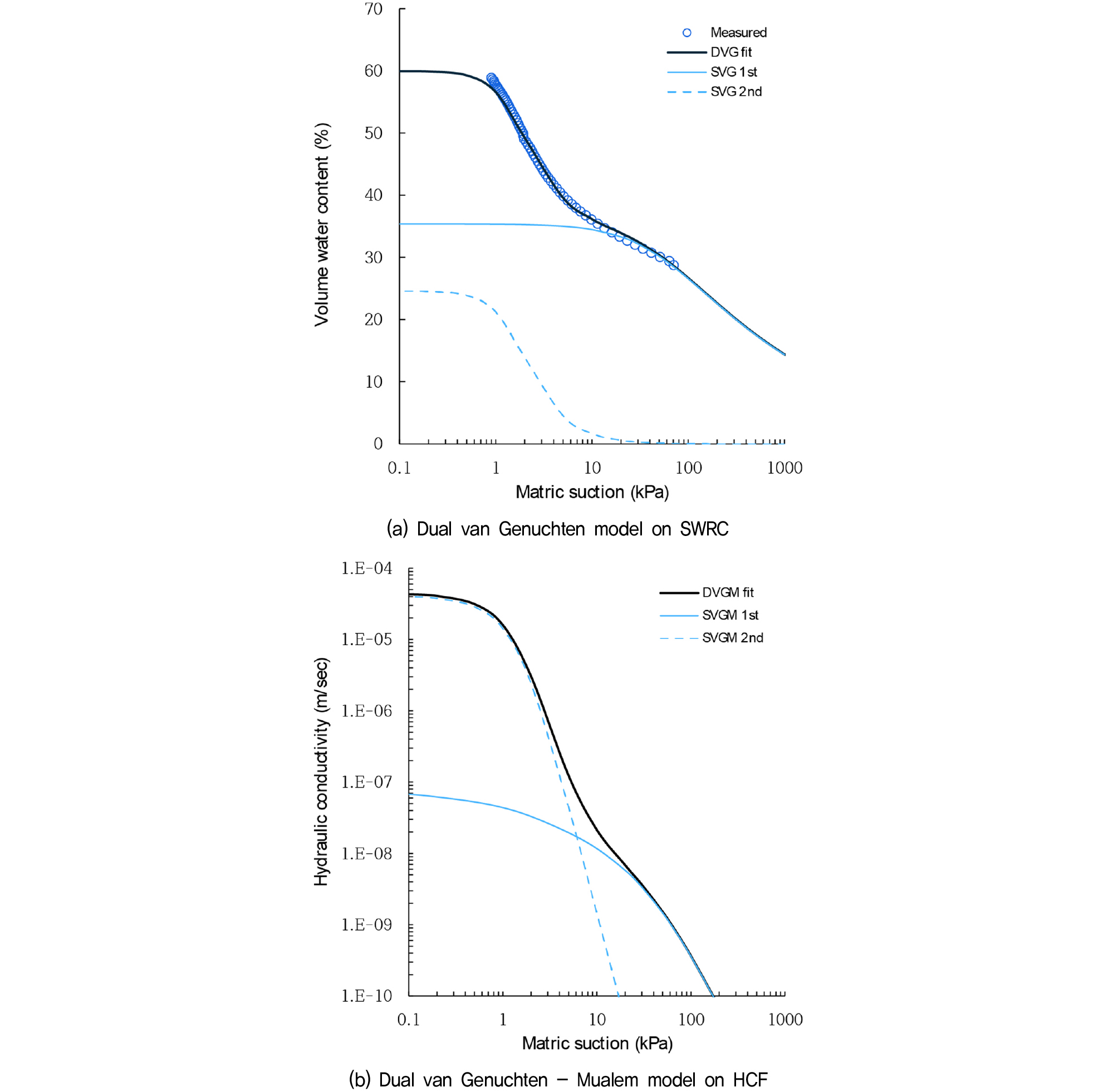
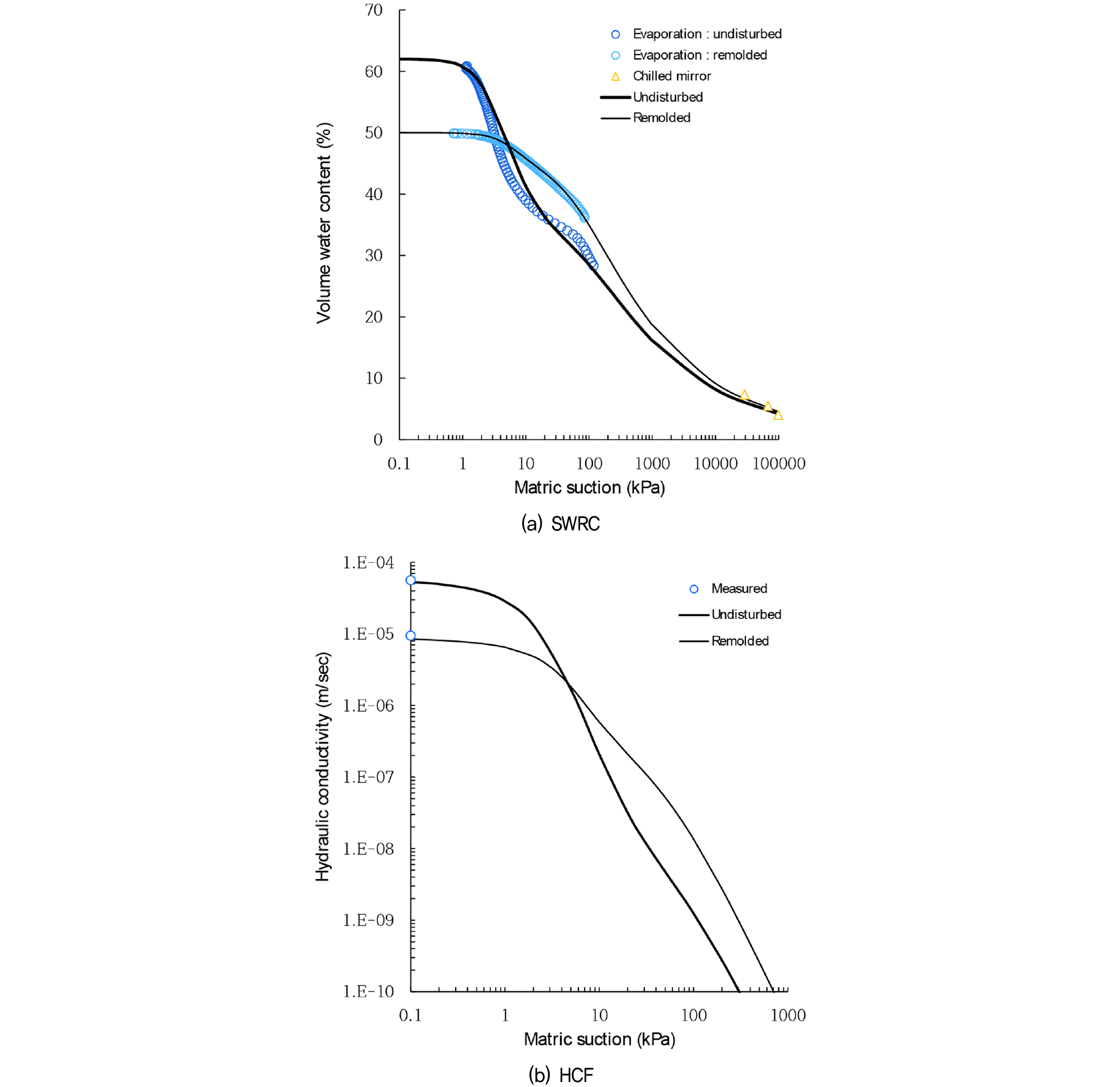
Fig. 1(a)에서 두 개의 SVG의 결합한 DVG 함수특성곡선 사례를 설명하고 있다. Fig. 1(b)에서는 SVGM 함수를 이중 결합한 DVGM 함수로 나타낸 불포화 수리전도도 함수(hydraulic conductivity function, HCF)를 보여준다. 역시 이중 함수특성곡선과 마찬가지로 두 개의 단일 투수계수 곡선에 중첩하여 새로운 곡선을 구하였다.
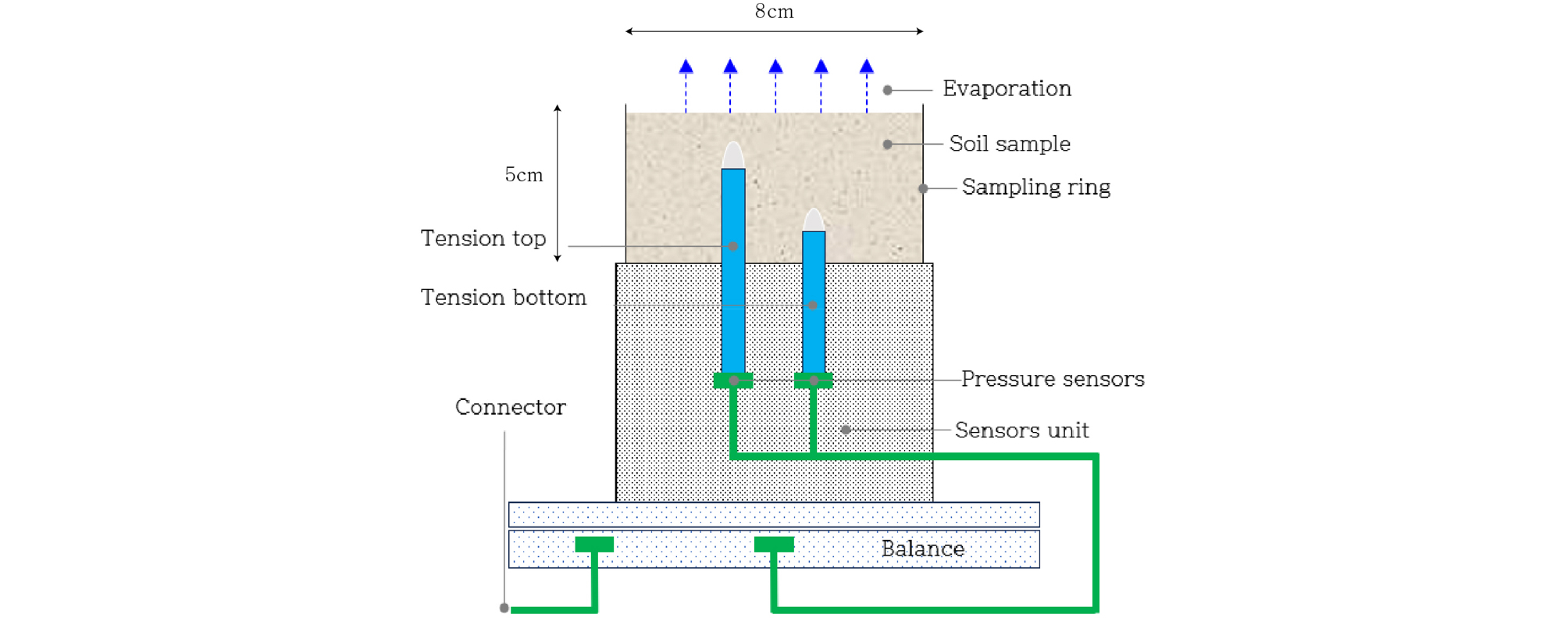
함수특성시험은 증발법과 냉각거울법 시험으로 수행하였다. Wind(1968)는 불포화토의 함수비 변화를 측정하기 위하여 증발을 유발시키고 질량 변화를 측정하는 증발법을 제안하였다. 이후 Schindler(1980)는 간소화된 증발법 시험으로 발전시켰으며 보다 넓은 모관흡수력 범위에서 함수특성곡선을 측정할 수 있다. Fig. 2에서 보여지듯이, 길이가 다른 장력계(tensiometer)가 삽입되어 각각 흡수력을 100kPa까지 측정한다. 장력계의 끝부분은 세라믹 재료로 간극수로 포화되어 있고 음의 수압을 측정할 수 있다. 또한 증발 과정 동안 저울이 질량 변화를 측정하여 시간에 따른 함수비 변화를 측정한다. 모관흡수력은 두 장력계에서 측정한 흡수력의 평균값으로 산정한다.
냉각거울법은 온도에 따른 포화 증기압 관계를 이용한 시험으로 시료의 온도와 냉각시킨 거울의 이슬점을 측정하여 상대습도를 구한 뒤, Kelvin 방정식을 이용하여 모관흡수력을 측정하는 방법이다(Oh et al., 2022). 높은 모관흡수력 영역의 데이터를 구할 수 있으며 증발법과 연계하여 사용하면 넓은 범위의 함수특성곡선을 잘 구할 수 있다.
산사태가 일어난 포항지역 세 지점에서 불교란시료를 채취하였다. 산사태 현장에서 증발법 시험 샘플 링(지름 8cm, 높이 5cm)을 사용하여 불교란 시료를 채취하였다. 시험 전 시료의 무게와 샘플링 질량을 측정하고 시험 후 24시간 건조 시킨 후 질량을 측정하여 건조밀도와 습윤밀도를 측정하였고 현장함수비를 산정하였다. 측정 결과, Table 1과 같이 간극비가 1.6~2.0 범위로 대단히 높고 건조밀도가 9.1~10.2kN/m3으로 대단히 낮게 측정되었다. 시료들은 팽창성이 매우 심하여 재성형한 시료를 24시간 포화 시킨 후 관찰하면 시료의 높이가 20~30% 정도 상승하는 것을 관찰할 수 있었다.
Table 1.
Physical properties of undisturbed samples
세 가지 시료의 입도분포는 모래크기(0.075mm~4.75mm) 입자가 50% 이상이며 실트크기(0.005mm~0.075mm) 입자가 12% 이상 분포하여 두 영역의 입도분포가 함수특성에 복합적으로 영향을 끼칠 수 있었다. 모두 통일분류는 SM으로 분류되었다. 또한 2μm 미만 입자는 평균 2.8%정도에 불과하지만 활성도가 1.25이상 나타나며 팽창성이 내재되어 있다고 판단된다.
불교란시료는 2022년 9월에 채취하였고 당시 강우로 인하여 지층의 포화도가 높은 시기였다. 계절적으로 건기에 현장에 다시 접근하여 팽창성이 덜한 상태에서 현장의 밀도를 측정하고 교란시료를 추가적으로 채취하였다. 교란시료는 이미 채취한 불교란시료와 유사한 물성을 보이는 것을 확인하고 Table 1에 나타난 현장 밀도에 맞추어 재성형하였다. 불교란시료와 재성형시료 모두 24시간 포화시켜 투수시험을 수행하였다. 포화투수계수는 변수위법을 수행하였다. 투수시험이 끝난 시료는 증발법 시험에 사용하였다. 또한 냉각거울법의 시험결과를 이용하여 모관흡수력이 큰 경우 함수특성곡선을 측정하였다. 불교란 시료는 지층이 극심하게 팽창한 상태의 거동을 보이고, 재성형시료는 팽창 이전 일반적인 상태에서 거동이 시작되는 것으로 판단되었다. 두 시료의 수리적 거동을 실험적으로 비교하는 것이 필요하였다.
증발법과 냉각거울법 시험을 수행하여, 팽창성 불교란시료와 재성형시료인 교란 시료의 함수특성곡선을 측정하여 비교하였다. Table 2에서는 3개 지역에 대한 van Genuchten 모델 계수를 정리하였다. 불교란시료의 포화 체적함수비가 0.54~0.62사이로 재성형시료보다 20%이상 높게 나왔으며 포화투수계수 또한 5배 이상 크게 측정되었다. 이는 불교란시료에서 간극비가 높고 건조밀도가 낮아서 기인한 것으로 판단된다.
Table 2.
Parameters for SWRCs
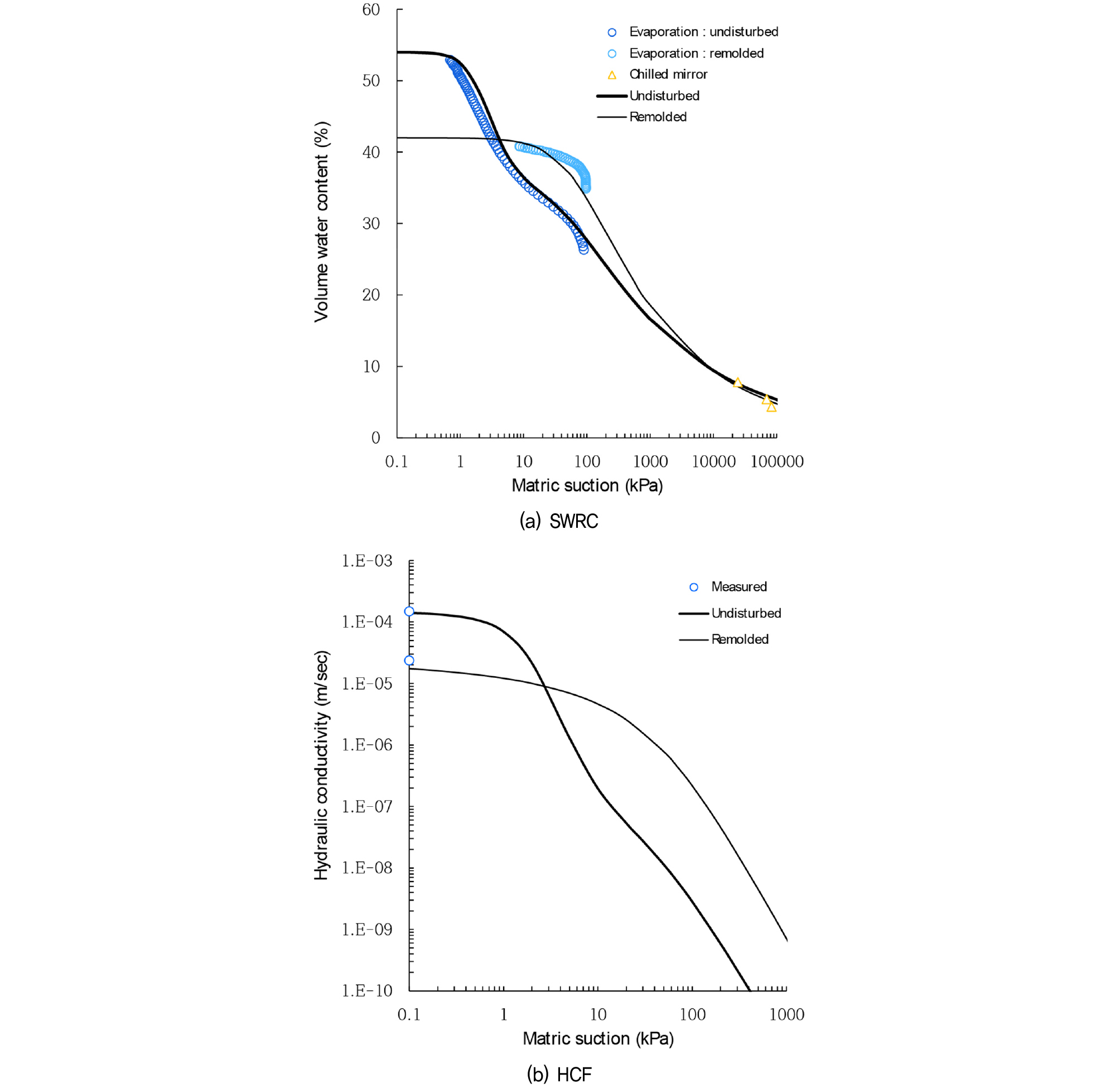
PH-1지역에서는, Fig. 3(a)에서 보여지듯이, 증발법 시험결과와 비교했을 때 불교란시료는 포화 체적함수비가 54%로 재성형시료보다 함수비가 28%정도 크며 함수특성곡선의 기울기, 즉 모관흡수력에 따른 체적함수비의 변화율이 더 큰 것을 확인할 수 있다. 냉각거울법 시험은 교란상태에서 수행하므로 두 시료간에 결과의 차이가 나타나지 않는다. 불교란시료의 함수특성곡선은 이중적인 곡선 형태를 나타내므로 DVG 모델로 피팅을 하였고 재성형시료의 곡선은 SVG 모델을 사용하였다. 불교란시료의 DVG 모델은 증발법 시험 및 냉각거울법 시험의 모든 모관흡수력 범위에서 잘 맞는 모습을 보여주고 있다. 재성형시료의 SVG모델은 각 시험 결과와 대체로 유사한 경향을 보인다. Fig. 3(b)에서 불포화 투수계수의 경우에, 불교란시료는 DVGM 모델을 사용하였고 재성형시료는 SVGM 모델을 적용하였다. 포화투수계수는 불교란시료가 1.48×10-4m/s이며 재성형시료 2.36×10-5m/s에 비하여 더 크게 측정되었으나 3kPa 이후의 불포화 투수계수는 불교란 시료가 급격하게 감소하여 재성형시료에 비하여 작게 나타난다.
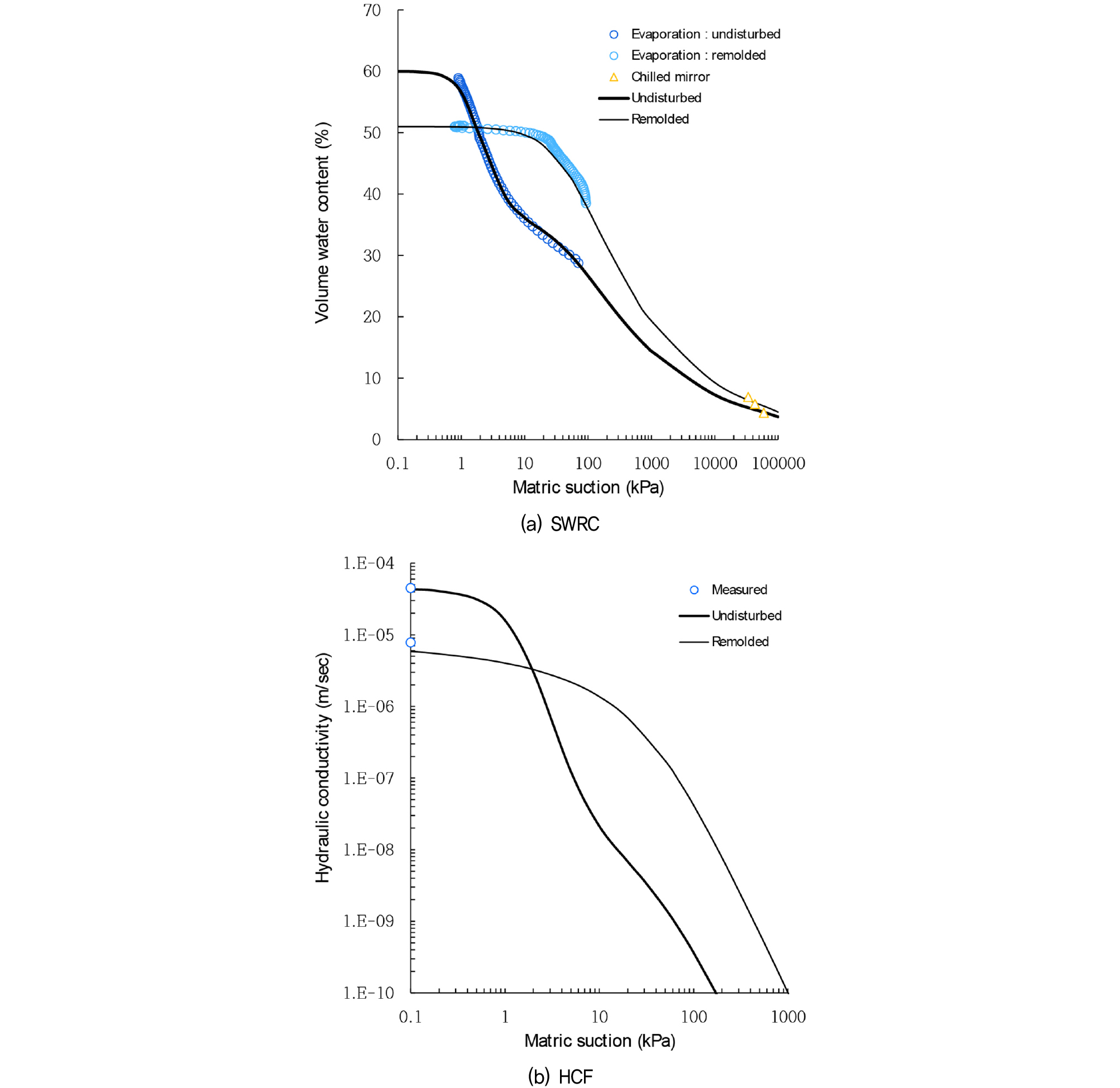
PH-2지역에서는, Fig. 4(a)에서 보여지듯이, PH-2지역의 불교란시료는 포화체적함수비가 60%로 재성형시료보다 함수비가 17% 정도 크다. 불교란시료 곡선은 DVG 모델로 피팅을 하였고 재성형시료 곡선은 SVG 모델을 사용하였다. 불교란시료와 재성형시료 곡선 모두 증발법 및 냉각거울법 시험과 일치하는 모습을 보인다. Fig. 4(b)에서 보여지듯이, 불포화 투수계수 함수는 불교란시료는 DVGM모델을 사용하였고 재성형시료는 SVGM 모델을 적용하였다. 포화투수계수는 불교란시료가 4.50×10-5m/s이며 재성형시료 7.82×10-6m/s에 비하여 크게 측정되었으나 2kPa 이후의 불포화 투수계수는 불교란시료가 재성형시료에 비하여 작게 나타나는 경향을 보인다.
PH-3시료의 경우, 불교란시료는 포화체적함수비가 60%로 재성형시료보다 함수비가 24%정도 크다. Fig. 5(a)에서 보이듯이, 불교란시료와 재성형시료 모두 DVG 모델로 피팅을 하였다. 불교란시료의 곡선은 증발법 시험결과와 대체로 비슷한 경향을 보인다. 재성형시료 곡선은 증발법 시험과 냉각거울법 시험결과와 모두 일치하는 경향을 보인다. Fig. 5(b)에서 보여지듯이, 불교란시료와 재성형시료의 투수계수는 모두 DVGM 모델을 사용하였고 포화투수계수는 불교란시료가 5.65×10-5m/s이며 재성형시료 9.46×10-6m/s이다. 또한 5kPa 이후의 불포화 투수계수는 불교란시료가 재성형시료에 비하여 작게 나타난다.
Lu and Likos(2006)는 불포화토의 흡수응력을 고려한 유효응력을 제시하였으며 흡수응력은 유효포화도에 따른 모관흡수력이 유효응력에 기여하는 정도를 나타낸다. 식 (5)와 같이 모관흡수력과 유효포화도의 곱으로 정의하였다(Oh et al., 2012).
여기서, σ'는 유효응력, σ는 전응력, σs는 흡수응력 (σ-ua) 순수직응력, ua는 간극공기압, uw는 간극수압이다.
불포화토의 전단강도는 식 (6a)와 같이 포화토와 마찬가지로 Mohr-Coulomb 파괴규준을 따른다. 식 (5)의 불포화토의 유효응력에 의한 파괴규준 식 (6b)와 같이 유도할 수 있다.
여기서, τf는 전단강도, ϕ'는 포화시 유효마찰각, c'는 포화시 유효점착력이다. 결과적으로 Fredlund et al.(1978)의 파괴규준과 동일한 형태이다.
아쉽게도 전단강도 시험을 위한 불교란시료는 확보할 수 없었고, 포화시 전단강도를 구하기 위하여 재성형 포화시료에 대한 직접전단시험을 수행하였다. 본 연구에서는 팽창시료의 초기조건(Table 1)에 맞추어 재성형 후 포화조건에서 직접전단시험을 수행하였고 포화시 점착력 0, 유효마찰각은 31°로 측정되었다. 하지만, 연직구속압 하에서 체적의 압축이 30% 이상 심하게 일어나고 결과를 신뢰하기 어려웠다. 세 지역에서 팽창 전 조건(Table 1)에 대하여 재성형한 시료는 포화시 직접전단시험을 성공적으로 수행할 수 있었다. 그 결과를 토대로 포화단위중량은 팽창상태 16kN/m3, 일반상태 18.5kN/m3, 포화시 점착력 24kPa, 유효마찰각 30°로 대표값을 구하였다. 따라서 팽창 전 후의 포화시 전단강도의 변화는 고려하지 않는 것으로 가정하였다. 추가적인 연구를 통하여 엄밀한 전단강도 계수를 적용한 해석을 수행할 필요가 있다.
3. 불포화 비탈면의 침투 및 안정해석
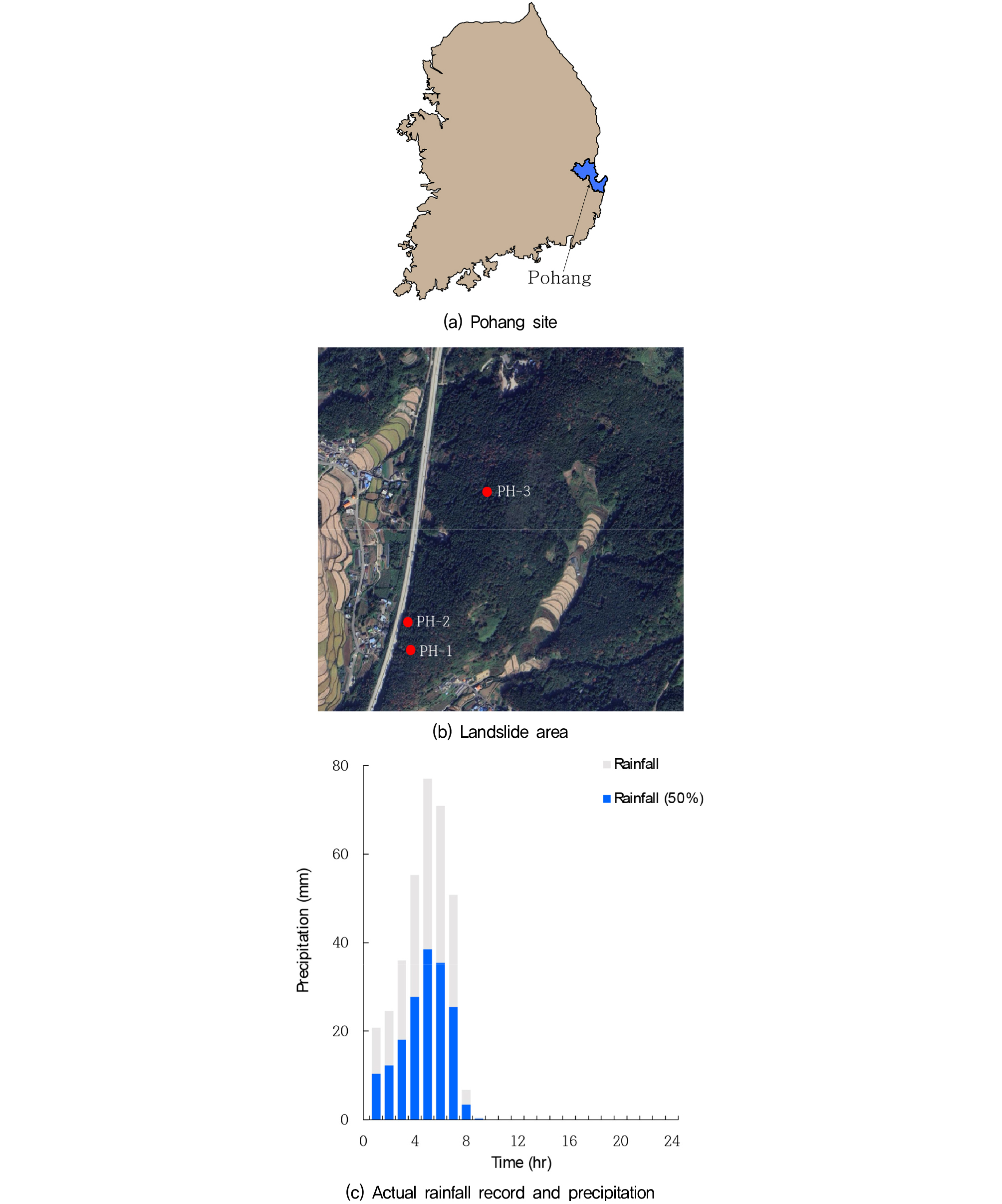
2022년 09월 06일 태풍 힌남노로 인하여 포항시 신정리 일대에 크고 작은 산사태가 여러 차례 발생하였다. 태풍 당일 약 342mm의 집중강우가 발생하였으며 Fig. 6(a)와 (b)에서 포항지역 산사태 지점을 보여준다. 침투해석을 수행하기 위하여 선행강우에 대한 정상류 해석과 집중강우에 대한 부정류 해석 시 강우 조건이 필요하다. 선행강우강도는 강우기간 2021년 07월부터 2022년 07월까지 1년간 강우량을 이용하였으며 유출 및 증발산을 고려하여 강우량의 50%로 2.35×10-8m/s(연강우량 약 675mm)를 적용하였다. 집중강우는 Fig. 6(c)와 같이 힌남노 상륙 당일 시강우량을 반영하였다. 침투 시 유출을 고려하여 강우량의 50%를 적용하였으며 총강우량은 1일간 171mm이다.
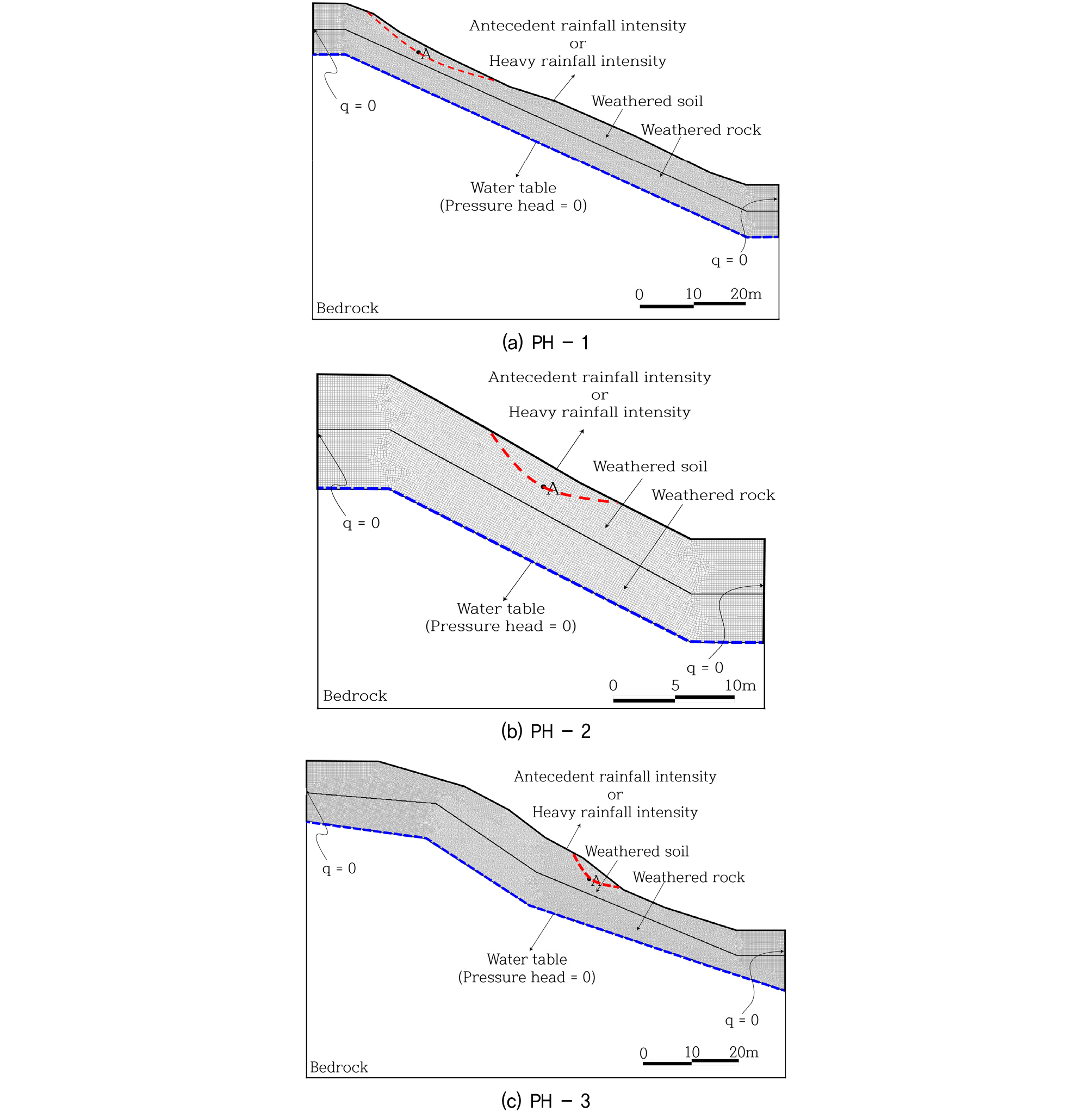
Fig. 7에서 보여지듯이, 지층은 지표면으로부터 풍화토, 풍화암, 기반암으로 이루어지고 풍화토와 풍화암의 깊이는 약 5m이다, 해석시 지하수위는 풍화암과 기반암 사이에 존재하는 것으로 가정한다. 또한 단면 좌우에는 유량을 0으로 경계조건을 설정하였다. 정상류 해석 시 지표면에 선행강우강도를 적용하였으며 부정류 해석 시에는 시간에 따른 집중강우강도를 입력하였다. 전절에서 기술하였듯이, 풍화토층에서는 실내시험을 통하여 함수특성곡선을 측정하였으며 직접전단시험을 통하여 포화상태 마찰각과 점착력을 측정하였다. 풍화암은 풍화토와 포화시 강도계수와 함수특성곡선은 같다고 가정하고 포화 투수계수는 절반으로 낮추어 설정하였다.
Geo-slope사의 Geostudio 2012 프로그램(2012a, 2012b)으로 정상류 및 부정류 침투해석을 수행하였다. 불교란시료와 재성형시료로부터 구한 수리역학적 특성을 입력하여 간극수압과 포화도를 계산하였다. 그리고 이러한 결과를 입력하여 불포화전단강도를 고려한 안정해석을 수행하고 시간에 따른 안전율을 비교하였다.
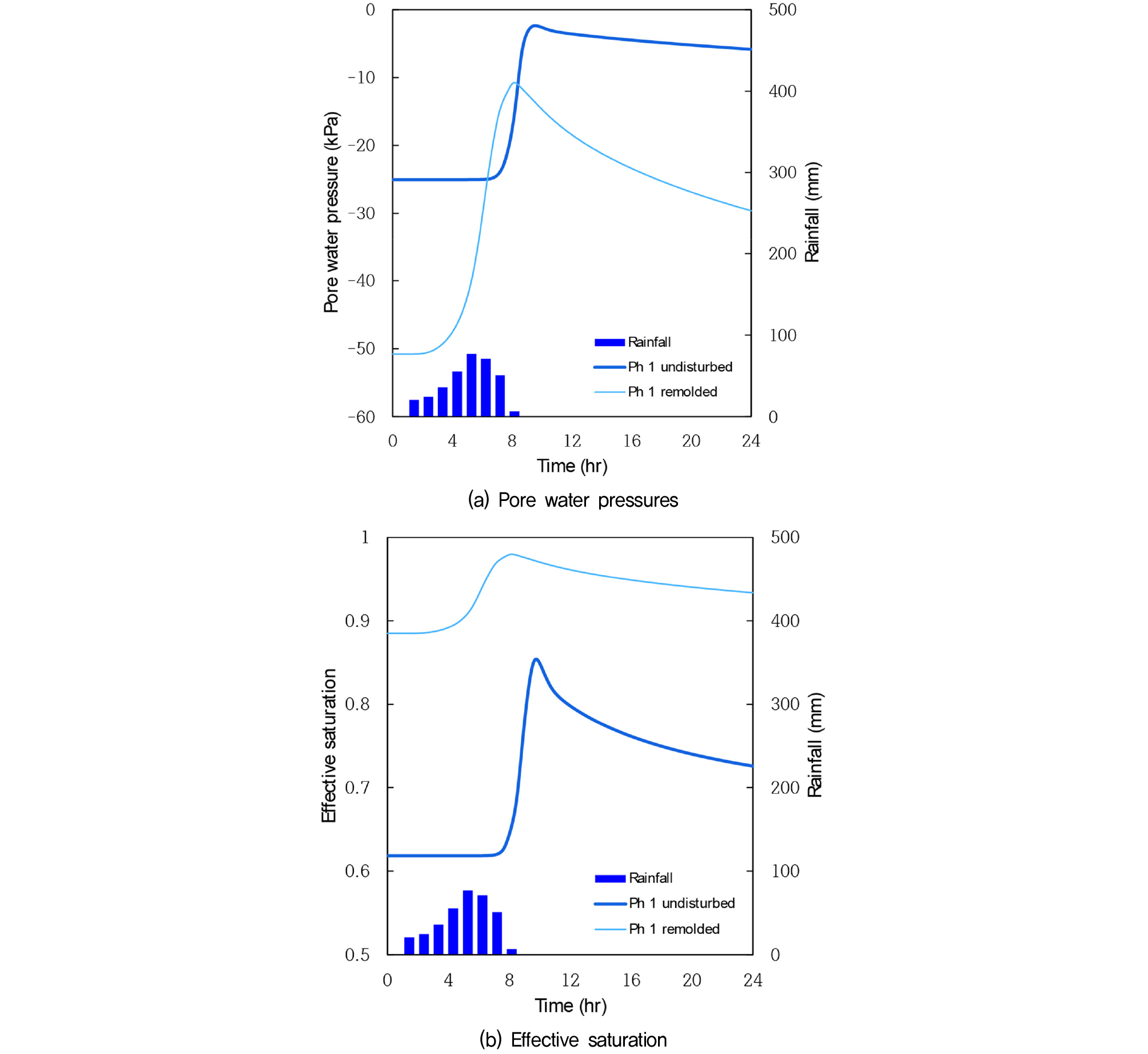
Fig. 8은 PH-1지역 파괴면 상의 A지점에서 시간에 따른 간극수압과 유효포화도의 변화를 보여주고 있다. Fig. 8(a)에서 보여지듯이, 불교란시료의 간극수압은 초기 -25kPa에서 강우지속시간 10hr 경과후에는 -2kPa까지 상승하였다. 재성형시료는 -51kPa에서 강우지속시간 8hr 경과시 -11kPa로 변화하여 간극수압의 변화는 재성형시료가 더 크게 나타난다. 하지만, 불교란시료의 간극수압은 0kPa에 접근하는 결과를 보였다. Fig. 8(b)와 같이 불교란시료의 유효포화도가 0.62에서 0.85까지 상승하였고 재성형시료는 0.88에서 0.97까지 상승하여 포화상태에 가깝게 도달하였다. 간극수압과는 상반된 형상을 보였으며 이는 함수특성곡선의 차이에 따른 효과로 보인다.
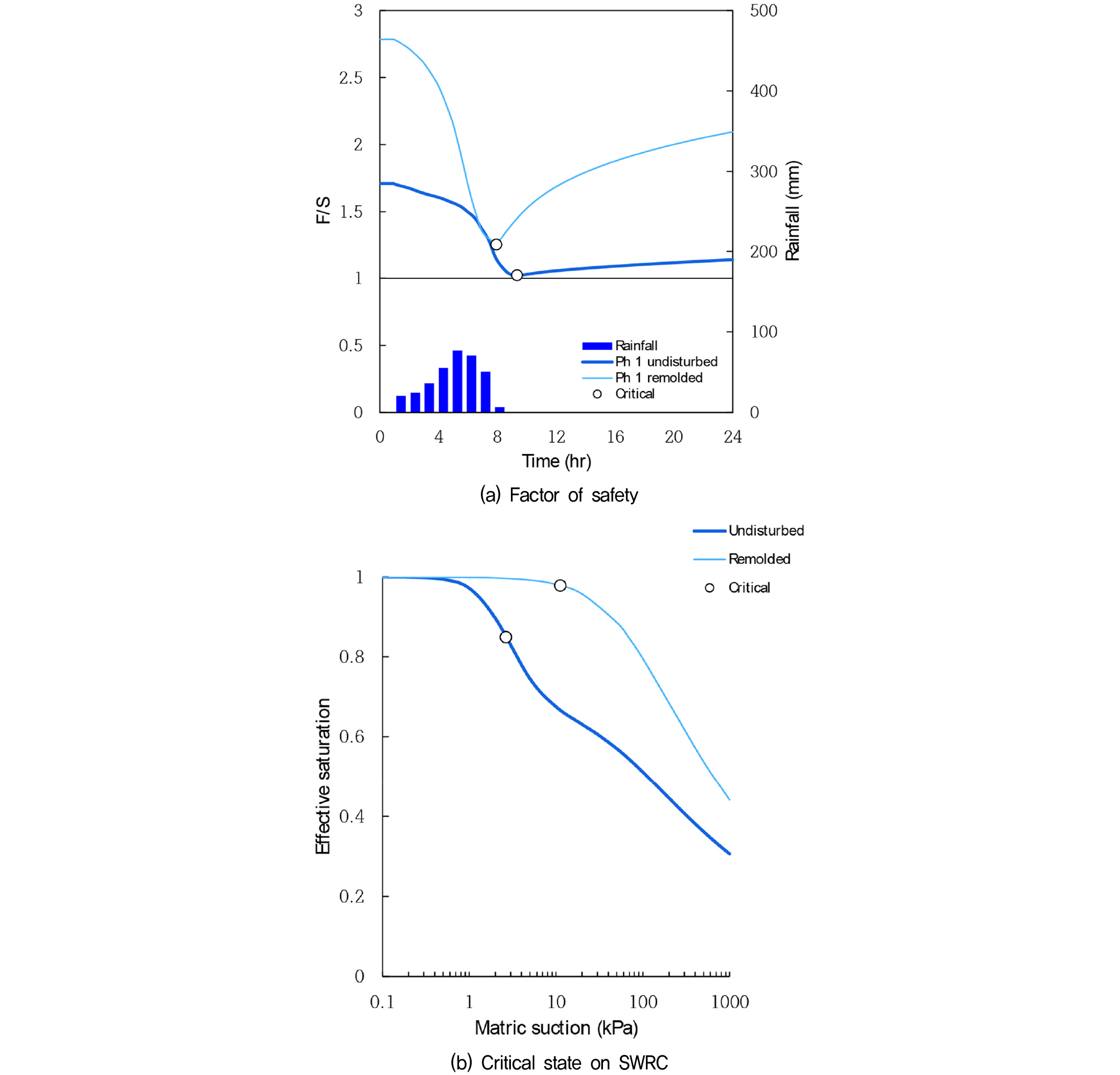
Fig. 9에서는 PH-1지역의 안정해석 결과를 보여준다. Fig. 9(a)에서 보여지듯이, 불교란시료의 시간에 따른 안전율은 초기 안전율 1.7에서 강우지속시간 10hr 경과시에 안전율이 1.02로 감소하여 안전율 1에 가까이 도달하는 결과가 나타났다. 실제 비탈면의 붕괴를 재현할 수 있었다. 한편 재성형시료는 초기 안전율 2.8에서 강우지속시간 8hr 경과시에 1.3으로 줄어들었으며 초기 및 최소안전율이 모두 불교란시료에 비하여 크게 나타났다. 이는 간극수압의 차이로 인한 효과로 판단되며 불교란시료는 초기 -25kPa에서 -2kPa로 상승하였고 재성형시료는 초기 -51kPa에서 -11kPa로 변화하였다. Fig. 9(b)에서는 A 지점에서 모관흡수력에 따른 유효포화도를 보여준다. 안전율이 최소인 취약 시점에서 비교 하였을 때, 재성형시료는 유효포화도가 불교란시료보다 높으나 모관흡수력은 더 큰 모습을 보인다. 이로 인하여 모관흡수력이 높을수록 유효응력이 높고 전단강도는 커지는 효과로 인하여 재성형시료의 안전율이 불교란시료보다 크게 나타난 것으로 보인다.
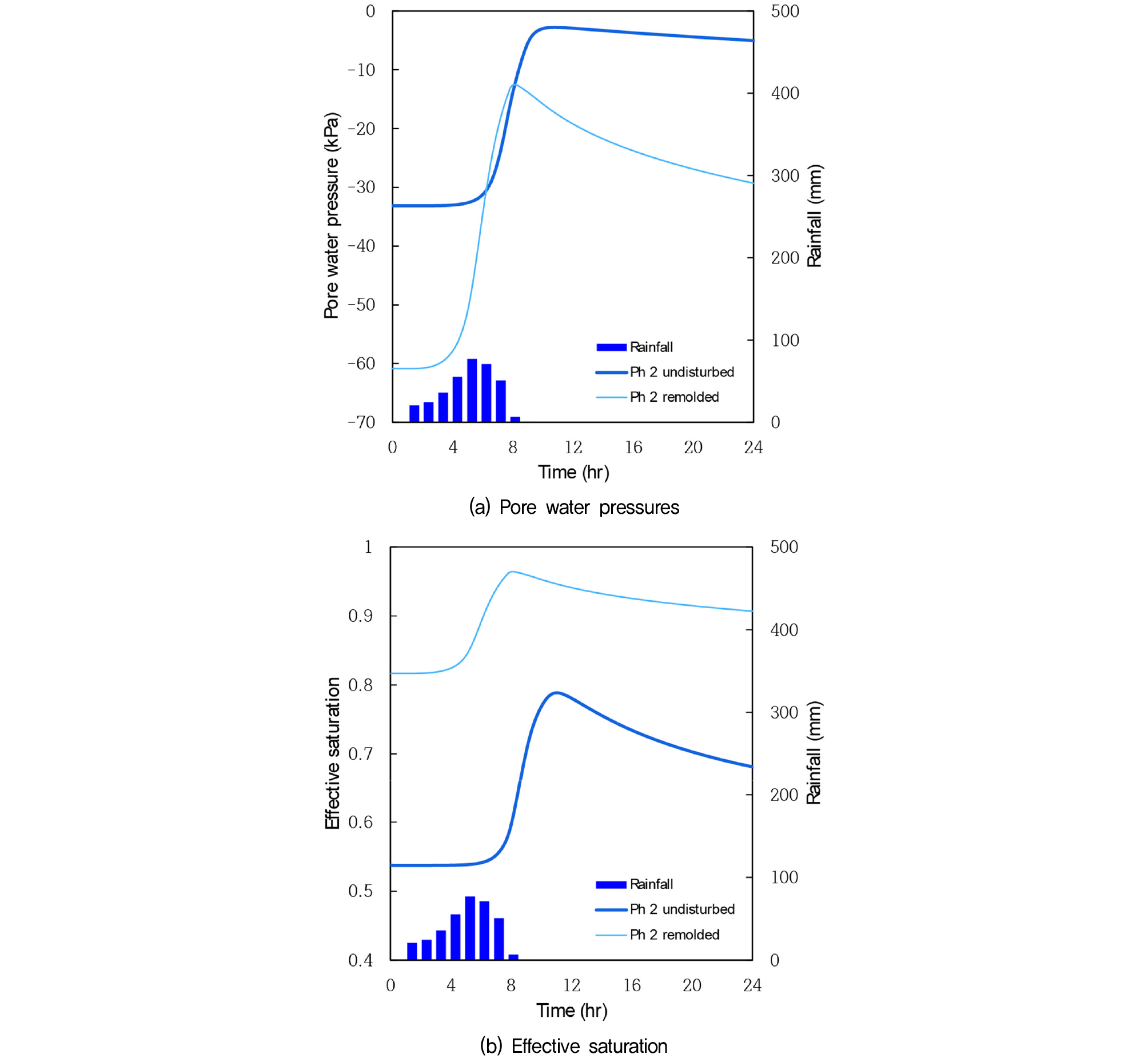
Fig. 10은 PH-2지역에서 나타난 파괴면 내 A지점에서 시간에 따른 간극수압과 유효포화도의 변화를 보여주고 있다. Fig. 10(a)에서 보여지듯이, 불교란시료의 간극수압은 초기 -33kPa에서 강우지속시간 11hr 경과후에는 -2kPa까지 상승하였다. 재성형시료는 -61kPa에서 강우지속시간 8hr 경과후에 -12kPa로 변화하였다. Fig. 10(b)와 같이, 불교란시료의 유효포화도가 0.53에서 0.78까지 상승하였고 재성형시료는 0.81에서 0.96까지 상승하여 포화상태에 가깝게 도달하여 간극수압과 유효포화도는 PH-1지역과 마찬가지로 엇갈리는 형상을 보인다.
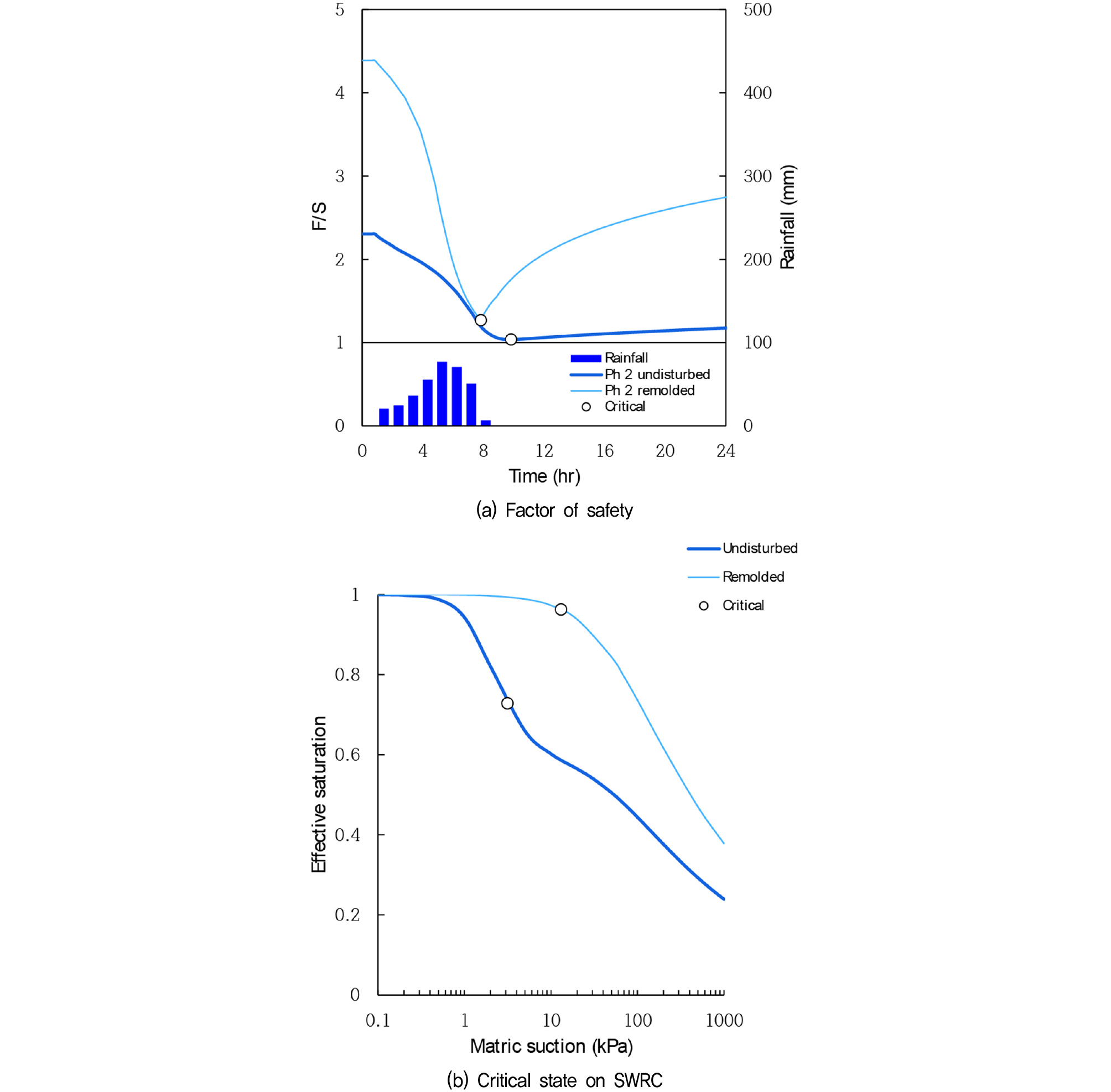
Fig. 11에서는 PH-2지역의 안정해석 결과를 보여준다. Fig. 11(a)에서 보여지듯이, 불교란시료의 시간에 따른 안전율은 초기 안전율 2.3에서 강우지속시간 10hr 경과시에 안전율이 1.03으로 감소하여 포항 1지역과 동일하게 안전율 1에 가까이 도달하였다. 따라서 불교란시료의 수리특성이 산사태로 인한 비탈면의 붕괴를 재현할 수 있었다. 반면 재성형시료는 초기 안전율 4.4에서 강우지속시간 8hr 경과시에 1.26으로 줄어들었으며 초기 및 최소안전율이 모두 불교란시료에 비하여 크게 나타났다. Fig. 11(b)에서는 A 지점에서 모관흡수력에 따른 유효포화도를 보여준다. 취약 시점에서 불교란시료의 경우에는 모관흡수력이 낮아서 전단강도가 재성형시료보다 작게 나타났다.
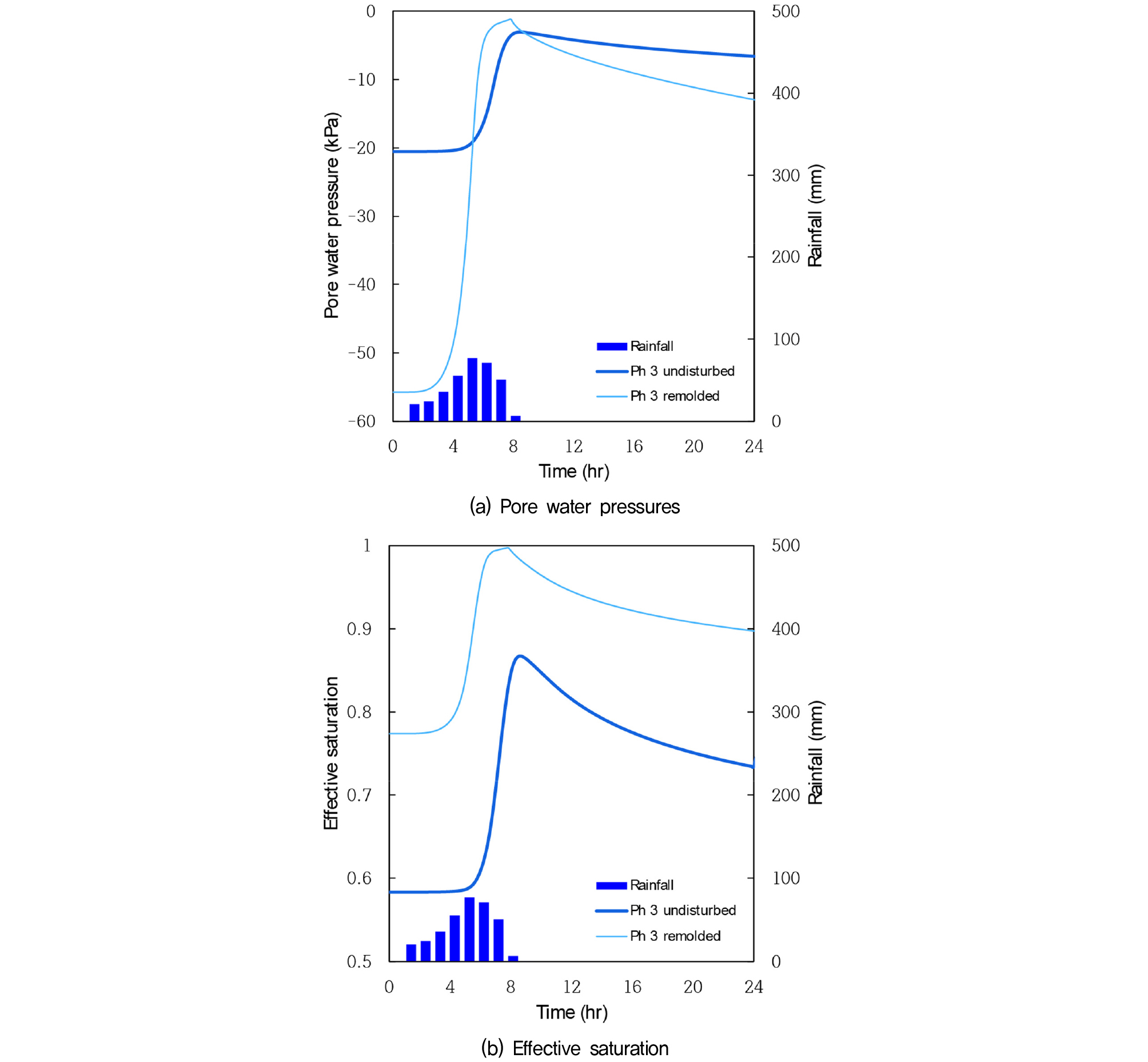
Fig. 12는 PH-3지역 A지점에서 시간에 따른 간극수압과 유효포화도의 변화를 보여주고 있다. Fig. 12(a)에서 보여지듯이, 불교란 시료의 간극수압은 초기 -20kPa에서 강우지속시간 9hr 경과후에는 -3kPa까지 상승하였다. 재성형시료는 -55kPa에서 강우지속시간 8hr 경과후 -2kPa로 변화하여 간극수압의 변화는 재성형시료가 더 크게 나타난다. Fig. 12(b)에서는 불교란시료의 유효포화도가 0.58에서 0.86까지 상승하였고 재성형시료는 0.77에서 0.99까지 상승하여 포화상태에 도달하였다.
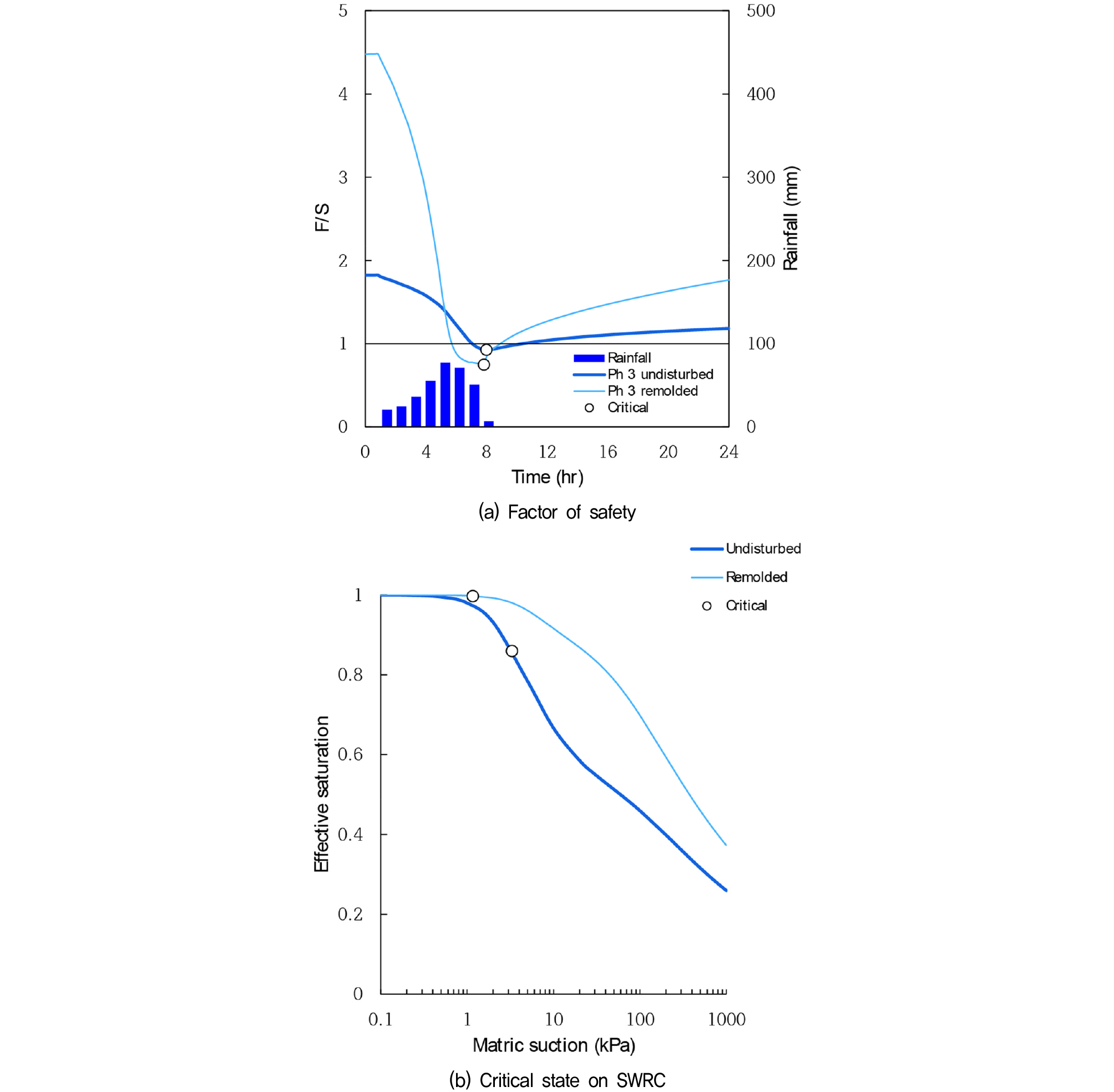
Fig. 13에서는 PH-3에 대한 안정해석 결과를 보여준다. Fig. 13(a)에서 보여지듯이, 불교란 시료의 시간에 따른 안전율은 초기 안전율 1.8에서 강우지속시간 9hr 경과시에 안전율이 0.92로 감소하였고 재성형시료는 초기 안전율 4.5에서 강우지속시간 8hr 경과시에 0.74로 줄어들었다. 다른 지역들과 달리 불교란, 재성형시료 모두 붕괴가 일어났으며 재성형시료가 더 낮은 안전율을 보인다. Fig. 13(b)에서는 파괴면 내 A지점에서 모관흡수력에 따른 유효포화도를 보여준다. 붕괴 시점에서, 재성형시료의 유효포화도는 높았지만 모관흡수력은 불교란시료보다 낮게 나타나서 안전율이 더 낮은 것을 알 수 있다.
포항지역에서는 태풍 힌남노로 인하여 집중강우가 침투하여 포화도가 증가하면서 지층은 점진적으로 팽창이 발생하였을 것이다. 이 지층이 겪은 간극수압과 포화도는 불교란시료와 재성형시료의 함수특성곡선 사이에 놓여 있을 가능성이 높다. 산사태가 일어난 시점에는 팽창된 시료의 함수특성에 근접하여 불교란시료의 함수특성곡선이 비탈면의 붕괴를 더 잘 예측하는 것으로 보인다.
본 연구에서는 팽창이 일어나기 전후의 상태를 비교하여 안정성에 미치는 영향을 검토하였다. 특히 팽창된 불교란 시료를 채취하여 함수특성곡선을 획득할 수 있어서 팽창시 수리특성을 침투해석에 적용하였다. 아쉽지만, 팽창성 불교란시료의 전단시험은 본 연구의 범위에 포함되지 않았다. 팽창에 따른 밀도 및 수리특성의 변화를 고려하여 엄밀한 수리-역학적 해석을 하기 위해서는 추가적인 연구가 필요하다.
4. 결 론
본 연구에서는 2022년 9월 태풍 힌남노로 인하여 무너진 포항시 신정리의 실제 산사태 발생지역을 대상으로 현장에서 직접 채취한 팽창성 불교란시료와 팽창이 일어나지 않은 재성형시료를 구분하였다. 증발법 시험을 기반으로 불교란시료와 재성형시료의 함수특성곡선을 획득하고 이중 van Genuchten 모델로 피팅하였다. 실제 강우조건에 대하여 2차원 침투해석 및 안정해석을 수행하였고 불교란시료와 재성형시료의 수리특성에 따른 차이를 비교하였다.
(1) 증발법 시험을 기반하여 불교란시료와 재성형시료의 함수특성곡선을 측정하였다. 불교란시료는 팽창이 일어난 상태여서 포화 체적함수비가 높았으며 모관흡수력에 따른 함수비 변화가 크게 나타나는 특징을 보였다. 팽창이전 상태에서 재성형한 시료는 함수특성곡선 및 투수계수함수에서 상이하게 나타났다. 이러한 함수특성곡선 실험결과를 이중 van Genuchten 모델과 단일 van Genuchten 모델로 매우 적절하게 나타낼 수 있었다.
(2) PH-1, 2 지역은 불교란시료의 침투해석시에는 강우가 지속됨에 따라 간극수압이 음의 값에서 증가하여 0kPa에 접근하는 모습을 보였다. 안정해석 결과, 집중강우가 지속될수록 불교란시료는 최소안전율이 1.0에 도달하여 실제 산사태를 재현할 수 있었다. 한편 재성형시료는 포화도는 매우 높지만 모관흡수력이 상대적으로 커서 안전율이 1보다 큰 값으로 나타났다. PH-3 지역은 강우가 지속됨에 따라서 불교란시료와 재성형시료 모두 비슷한 수준의 간극수압에 도달하였다. 안전율은 불교란시료가 재성형시료보다 초기 안전율이 낮게 보였으며 강우가 지속될수록 불교란시료와 재성형시료는 안전율 0.9, 0.7로 감소하였다. 불교란 시료의 경우에 실제 산사태를 더 잘 반영하는 것으로 여겨진다.
(3) 포항지역에서는 팽창성 지반이 산사태에 영향을 끼친다. 팽창이 일어난 불교란 시료로부터 수리특성을 획득하였으며, 이로부터 파괴시 간극수압과 안전율을 합리적으로 예측하는 것으로 가능하였다. 추후 팽창성 시료에 관한 심화된 실험과 체계적인 연구를 진행하여 비탈면 안정성 평가에 대한 신뢰성을 높이는 것이 필요하다.