1. 서 론
2. 수치해석모델 검증
2.1 원심모형실험 개요
2.2 수치해석모델
2.3 지반 구성 모델
2.4 원심모형실험과 수치해석모델의 결과 비교
3. 베이스먼트 수치해석모델
3.1 베이스먼트 케이스 선정
3.2 지반 프로파일 및 물성 선정
3.3 입력지진파 선정
4. 수치해석 결과
4.1 자유장 지반최대가속도
4.2 래킹(Racking) 및 유연도(Flexibility) 비율
4.3 지진토압증분계수
5. 결 론
1. 서 론
일반적으로 지하구조물은 지진토압으로 인한 구조적 손상에 지상구조물보다 상대적으로 덜 취약한 것으로 간주되었다. 그러나 San Fernando 지진에 노출됐던 철근콘크리트 지하 저수지 및 Kobe 지진에 노출된 Dakai 지하철역 등의 파괴사례는 지하구조물의 종합적인 지진 취약성 평가의 필요성을 강조한다. 근래 지하구조물 내진설계에 있어 지진토압의 추정은 기존에 중력식 옹벽 및 캔틸레버식 옹벽에 대하여 제안된 지진토압식을 주로 사용하고 있다(Kim et al., 2014). 기존의 지진토압식들은 주로 해석적 방법과 경험적 방법으로 제안되었다.
해석적 방법은 크게 한계상태법(Limit state method), 탄성법(Elastic method)과 탄소성법(Elasto-plastic method)으로 나뉜다. 한계상태법에 기반하여 제안된 Mononobe(1929)와 Okabe(1924) 토압식은 지하구조물에 대한 동적토압 및 지진토압 계산에 많이 사용되는데, 이는 지반 쐐기의 관성력만을 동적 힘으로 고려하며 벽의 관성력은 고려되지 않는다. 한계상태법에 기반하여 제안된 또다른 토압식인 Seed and Whitman(1970) 토압식은 전체토압을 정적 및 동적토압으로 분리하였고, 최대지반가속도(PGA)의 80%를 활용하여 작용점이 벽 높이의 0.6배(0.6H)인 역삼각형 분포의 동적토압을 제안하였다. 탄성법에 기반하여 제안된 토압식은 주로 Wood(1973) 토압식이 많이 사용되는데, 이는 단단한 강체로 간주되는 U자형 옹벽에 대하여 옹벽의 종횡비(L/H)를 고려하여 제안되었다. 이때 벽에 가해지는 토압은 흙의 유사 정적 체적력(body force)를 바탕으로 계산되었기 때문에 지진파가 지반 내에서 전파됨에 따라 일어나는 증폭 등은 현상은 고려되지 않았다. 탄소성법에 기반하여 Veletsos and Younan(1994)은 진동 및 순간 하중을 받는 질량이 없다고 가정한 강체 벽에 대하여 회전강성의 영향을 고려하는 해석해를 제시하였다. 이들의 추가 연구는 벽의 굽힘 및 회전강성의 영향을 모두 고려하였는데, 이때 회전 및 평행이동에 대한 유연성이 증가하면 벽에 가해지는 동적토압이 감소된다는 것을 밝혀냈다. 또 토압의 작용점은 강체 및 비강체 벽 전부 벽 높이의 0.3에서 0.4배 사이에 분포하는 것으로 제시하였다. 해석적 방법을 바탕으로 제안된 기존의 토압식들은 구조물의 종횡비를 대부분 고려하지 않았으며, 동적 하중은 유사정적 방법을 활용하여 계산하였기 때문에 지진파가 기반암에서 지표로 전파되며 발생하는 증폭이나 관성 효과를 고려하지 못하였다.
경험적 방법은 주로 원심모형실험을 많이 사용한다. Al Atik and Sitar(2010)는 강체 및 비강체 U자형 보강 지하구조물에 대한 원심모형실험을 실시하여, 측정된 동적토압증가분이 깊이에 따라 선형적으로 증가하는 삼각형 모양의 분포로 나타난다고 제시하였다. 이때 벽에서 측정된 동적토압증분과 관성력의 사이에는 위상차가 나타났다. 또 비강체 구조물에 대한 자유장에서의 최대지반가속도와 동적토압증분계수(ΔKae) 간의 관계는 PGA< 0.4g일 때 무시할 만큼 작음을 보였다. Geraili Mikola et al.(2016)는 강체 및 비강체 캔틸레버 벽에 대해 원심모형실험을 수행하였다. 스트레인 게이지로부터 계산된 동적토압은 깊이에 따라 선형적으로 증가하는 것으로 나타났고, 작용점은 기초에서 1/3H에 위치하였다. Wagner and Sitar(2016)는 13.3m 높이의, 3개의 층에서 가새로 보강된 강체 베이스먼트 지하구조물에 대해 원심모형실험을 수행하였다. 동적토압의 분포 형상을 지반과 구조물의 상대적 유연성에 따라 포물선형, 입방형, 역입방형 형상으로 제안하였다. 경험적 방법으로 수행된 원심모형실험들은 강체 및 비강체의 기준이 모호하였고, 구조물의 형상이 다양하지 않아 종횡비(L/H)가 동적 토압에 미치는 영향을 평가하지 못하였다.
종합적으로, 동적토압 또는 지진토압은 지반과 구조물 사이의 상대적 유연비, 지진파의 강도, 구조물의 종횡비(L/H) 등의 요인에 의해 영향을 받는다는 것이 분명하다. 그러나 Table 1에서와 같이 종횡비(L/H)와 유연비를 통합적으로 고려하여 지하 구조물의 동적토압을 예측하는 토압식은 부족한 현황이다. 본 연구에서는 구조물의 종횡비 및 지반에 대한 구조물의 상대적 강성 또는 유연비가 동적토압에 미치는 영향을 종합적으로 확인하여 기존 토압식들의 신뢰성 및 적용성을 평가하고자 하였다. 이를 위해 많은 동적 수치해석 케이스를 통해 매개변수 연구를 수행하였다. 이때 대상 지하구조물은 다양한 종횡비와 구조적 강성을 가지는 베이스먼트의 형상을 띄는 케이스들을 가정하였다.
Table 1.
Summary of studies on dynamic earth pressure on walls
| Reference | Typology | Method | Aspect ratio, L/H | Relative Flexibility |
| Mononobe and Matsuo (1929) | Retaining walls | 1g experiments | Not available | Not available |
| Seed and Whitman (1970) | Retaining walls | Analytical solution | Not available | Not available |
| Veletsos and Younan (1994) | Retaining walls | Analytical solution | Not available | Not available |
| Al Atik and Sitar (2010) | U-shaped basement walls | Centrifuge | 1.92 | Stiff, Flexible |
| Gerali Mikola et al. (2016) | U-shaped basement walls with struts | Centrifuge | 1.67 | Stiff |
| Wagner and Sitar (2016) | U-shaped deep basement walls with struts | Centrifuge | 0.44 | Stiff |
2. 수치해석모델 검증
2.1 원심모형실험 개요
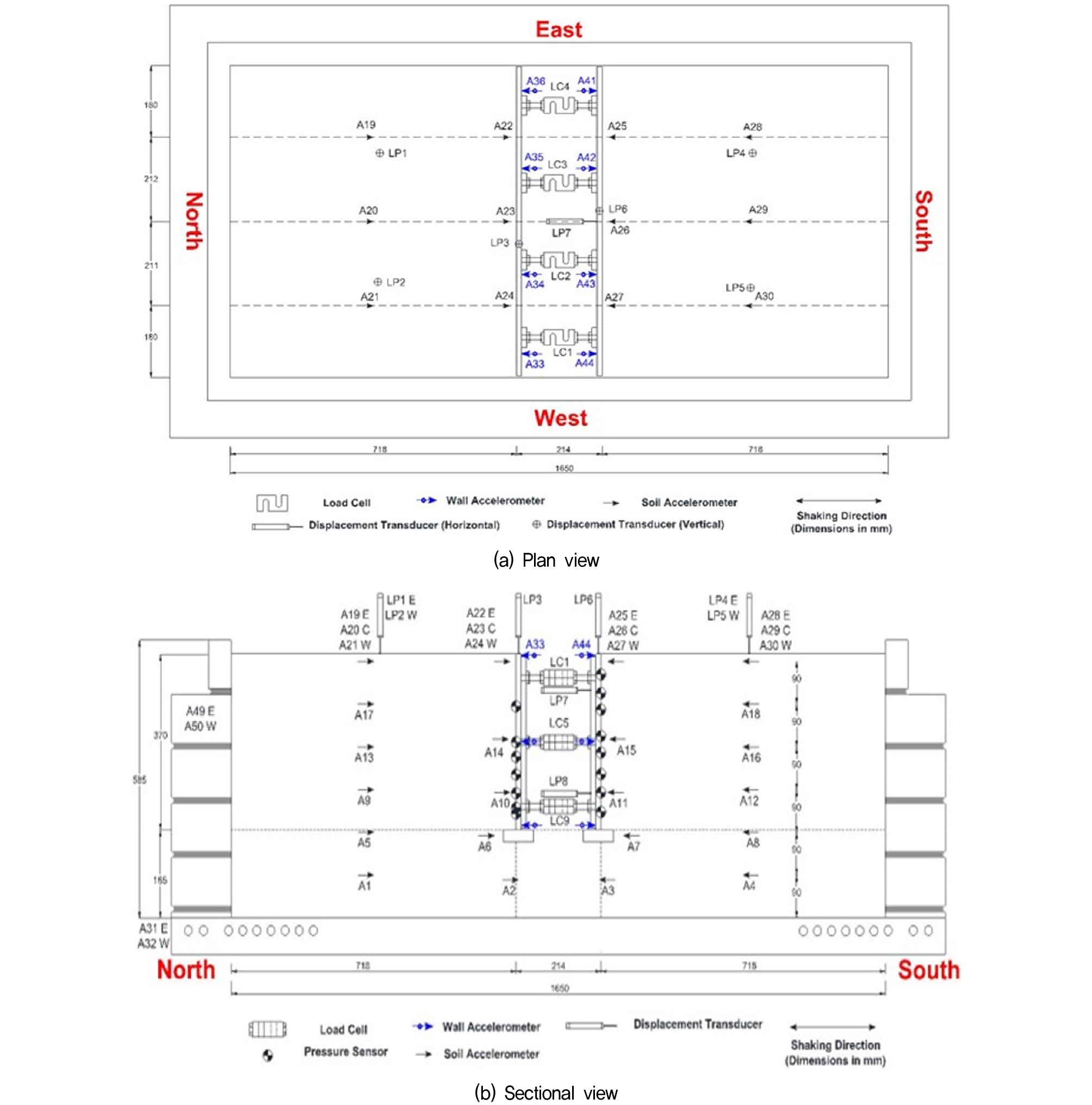
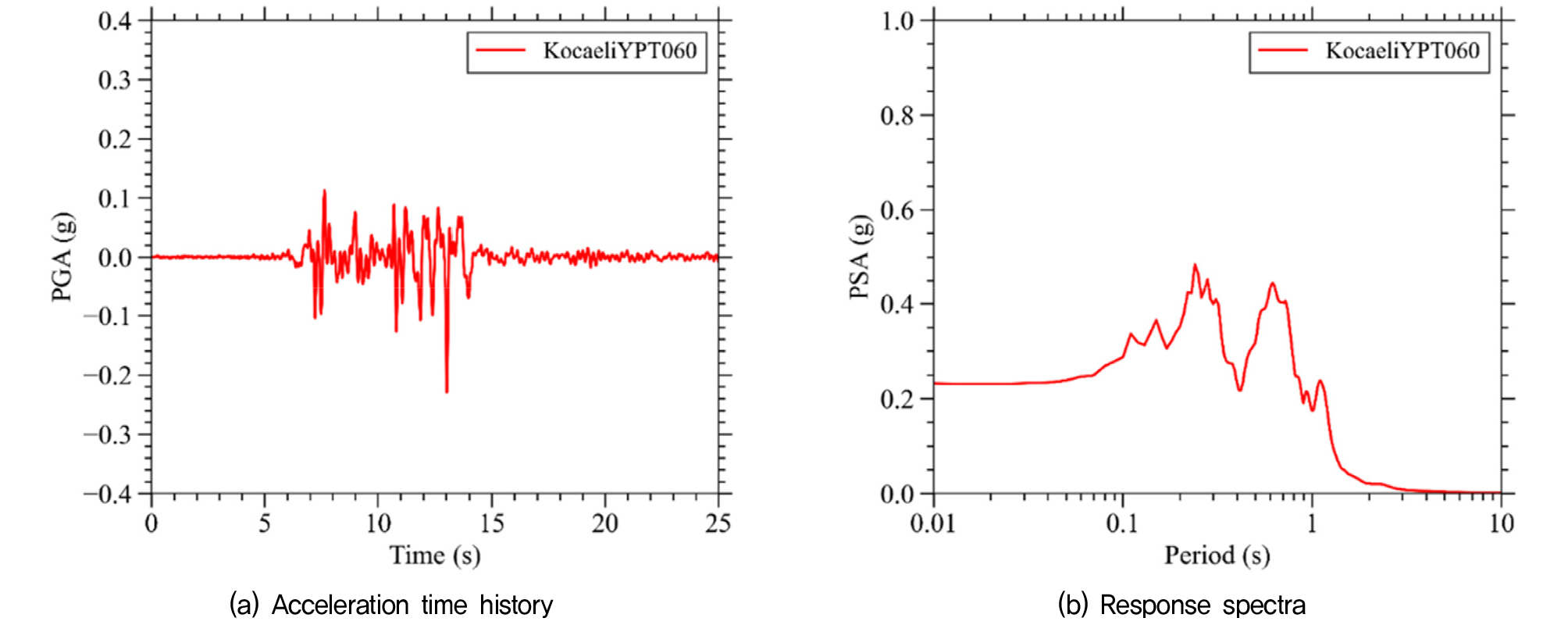
본 연구에서 수행하고자 하는 옹벽 및 흙막이벽에 대한 사례의 부족으로 Wagner and Sitar(2016)의 원심모형실험 검증 연구를 준용하였다(Yun et al., 2022; Jo et al., 2013). 원심모형실험에서는 1/36 상사비의 가새 보강 강체 베이스먼트가 중력가속도 36g 하에 사용되었고 베이스먼트 벽체에서 지진토압을 측정하였다. 높이 13.23m의 지하 벽은 3개 층에서 가새로 보강되었으며, 최하단 기초는 보통조밀한 모래 위에 위치되었다. Fig. 1은 원심모형실험에 사용된 가속도계와 스트레인 게이지의 배치도이다. 지반은 건조한 보통조밀 모래(Nevada Sand)를 사용하였고, 모형 하부에서 계측된 입력지진파의 가속도 시간이력 및 가속도 스펙트럼은 Fig. 2와 같다. 또, 베이스먼트 및 Nevada Sand의 물성과 사용된 입력 지진파의 세부적인 특성은 각각 Table 2, 3, 4와 같다.
Table 2.
Structural properties of model and prototype per unit width
Table 3.
Properties of Nevada sand used in centrifuge experiment
| Specific gravity, Gs | emin | emax | γd,min (kN/m3) | γd,max (kN/m3) |
| 2.66 | 0.510 | 0.784 | 14.86 | 17.24 |
Table 4.
Characteristics of input motion
| Earthquake name | Station name | PGA (g) | Ia (cm/s) | D5~95 (s) | Tp (s) |
| Kocaeli | YPT060 | 0.23 | 25.0 | 6.6 | 0.24 |
2.2 수치해석모델
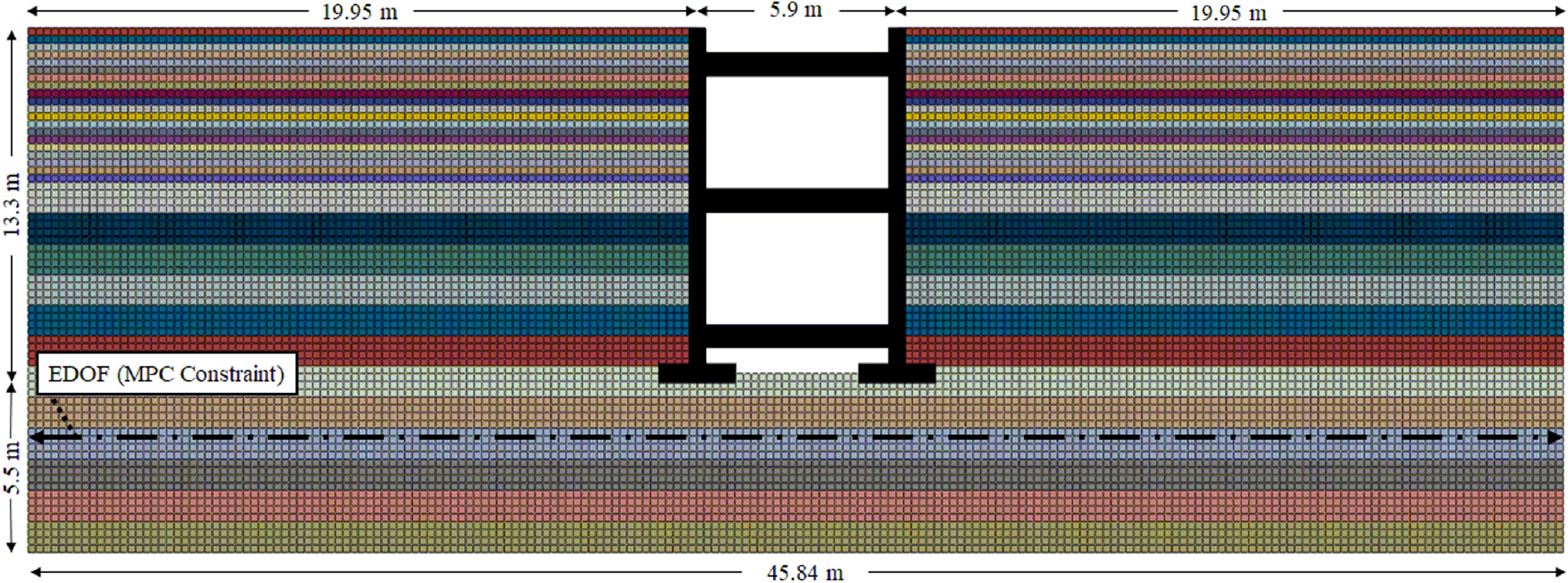
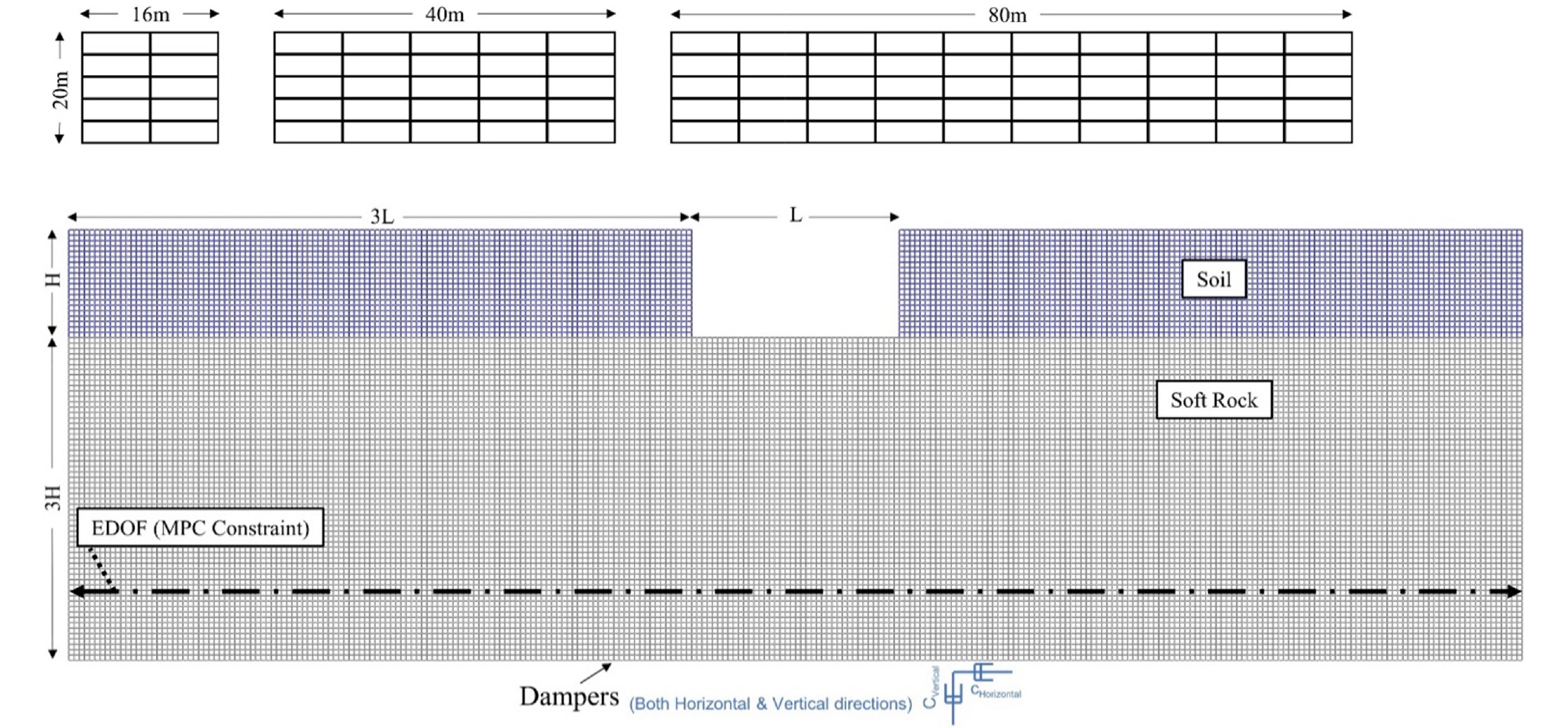
수치해석모델은 상용 유한 요소 해석 프로그램인 ABAQUS 6.12(2012)를 사용하여 구축하였다. Fig. 3과 같이 베이스먼트와 주변지반을 2차원 평면 변형 모델로 모델링하였다. 토층 및 기반암은 CPE4R(4-node bilinear, reduced integration with hourglass control) 요소를 사용하였고, 베이스먼트는 B21(Beam, linear in plane) 요소를 사용하였다.
모델의 단순전단을 재현하기 위해 ABAQUS의 다점제약조건(MPC) 옵션을 사용하였다. 다점제약조건(MPC)은 해석이 진행될 때 연결된 점들의 자유도가 동일하도록 제한하여 함께 거동하게끔 만들어준다. 모델의 양쪽 측면 경계를 다점제약조건(MPC)으로 연결하여 모델의 수평 방향으로 무한히 확장되는 것으로 추정되는 실제 지반의 자유장 조건을 모사하였다. 지반과 구조물 인터페이스는 ABAQUS의 Surface-to-Node 인터페이스를 적용하였다. Surface-to-Node 인터페이스는 해석 모델에서 특정 표면과 개별 노드 사이의 접촉을 정의하는 방법으로, 표면과 점 사이의 상호 작용을 보다 정확하게 모사할 수 있다. 이때 인터페이스의 마찰각 tanφinterface=2/3·tanφsoil≈0.33을 사용하였다(Deng et al., 2016; Zhang et al., 2017). 이를 통해 베이스먼트의 벽과 지반 사이의 떨어짐을 허용하여 벽에서 지반으로 인장 응력이 전달되지 않도록 하였다.
2.3 지반 구성 모델
원심모형실험에서 추정한 것과 동일하게 Nevada 모래의 밀도는 깊이에 따라 제곱근 분포로 가정하였고, 각 지반 레이어의 공극률 은 식 (1)을 사용하여 계산하였다.
Hardin(1978)의 식 (2)를 사용하여 기준 전단 계수(Reference shear modulus)인 를 각 레이어 별로 계산하였고,
각 레이어의 최대전단탄성계수 및 전단파속도 를 식 (3)과 (4)를 사용하여 계산하였다.
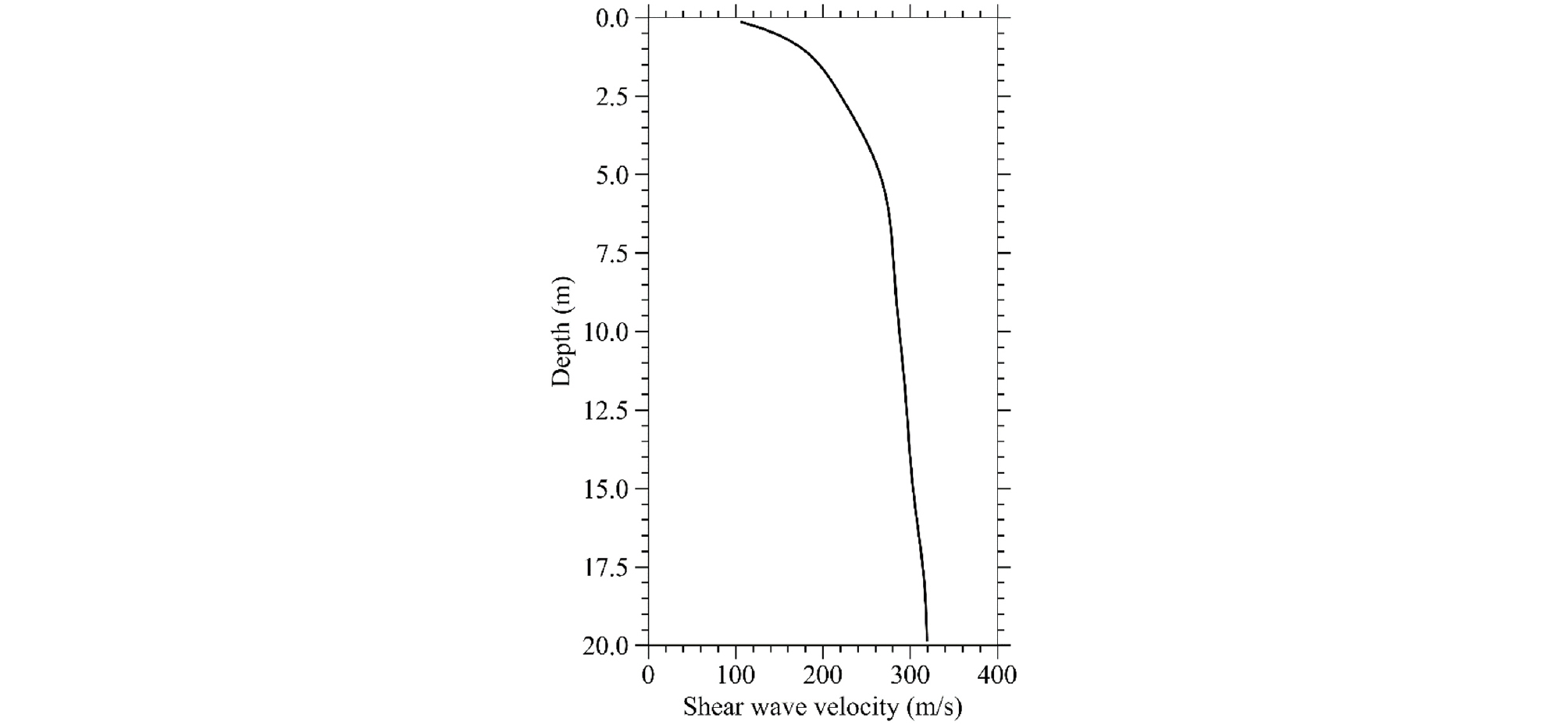
결과적으로 도출되는 전단파 속도 분포는 Fig. 4와 같다.
각 토층의 등가선형(EQL) 물성들을 얻기 위해 DEEPSOIL v.7(2024) 소프트웨어를 사용하였다. 등가선형(EQL) 물성들은 터널 구조물의 동해석에 많이 사용되는데, 흙의 비선형 거동에 대한 효과적인 근사치로서 사용할 수 있으며 선행연구에서 사용된 사례가 많다(Cilingir and Madabhushi, 2011; Tsinidis et al., 2016; Argyroudis et al., 2017).
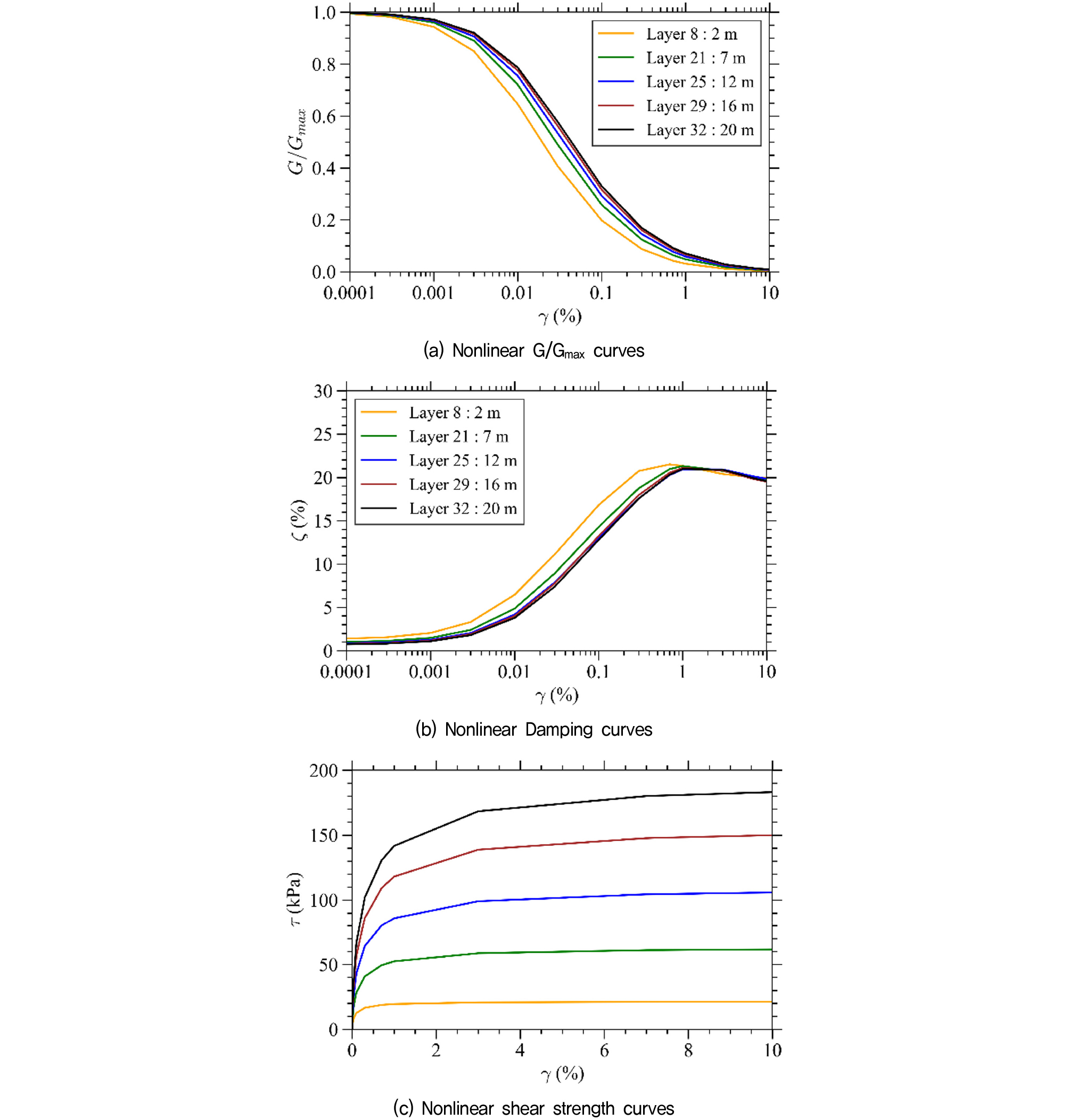
본 연구에서는 원심모형실험의 지반을 32개의 층으로 나누어 각 층에 대하여 전단강도를 고려할 수 있는 GQ/H(General Quadratic Hyperbolic) 구성 모델을 활용하여 전단변형률에 대하여 비선형 전단탄성계수 곡선, 비선형 감쇠곡선, 비선형 전단강도 곡선을 생성하였다(Groholski et al., 2016). 이때 Darendeli(2001)의 곡선을 기준 곡선(Reference curve)는 사용하였고 입력 파라미터로 과압밀비(OCR) 1.0, 정지토압 계수(K0) 0.46, 소성지수(PI) 0, 하중 주기 수(N) 및 주파수(f) 10 및 1.0Hz을 사용하였다. 또, Kwok et al.(2007)에서 이 제안한 지침에 따라 Rayleigh 감쇠를 첫 번째 및 다섯 번째 모드를 기반으로 계산하여 소변형률에서의 감쇠를 반영하였다. 결과적으로 각 층마다 Non-masing 규칙에 따라 생성된 비선형 곡선들은 Fig. 5와 같다(Phillips and Hashash, 2009).
이를 바탕으로 DEEPSOIL v.7(2024) 소프트웨어로 1차원 비선형 지반응답분석(GRA)을 수행 후, 해석 결과에서 계산된 각 층의 최대전단변형률의 0.65배에 해당하는 전단변형률(유효전단변형률)을 계산하였다. 그 후, 각 층의 비선형 응답 곡선에서 각 층의 유효 변형률 값에 해당하는 등가선형(EQL) 물성들을 계산하였다. 이렇게 도출한 등가선형 물성들을 수치해석모델의 지반영역에 사용하였다.
2.4 원심모형실험과 수치해석모델의 결과 비교
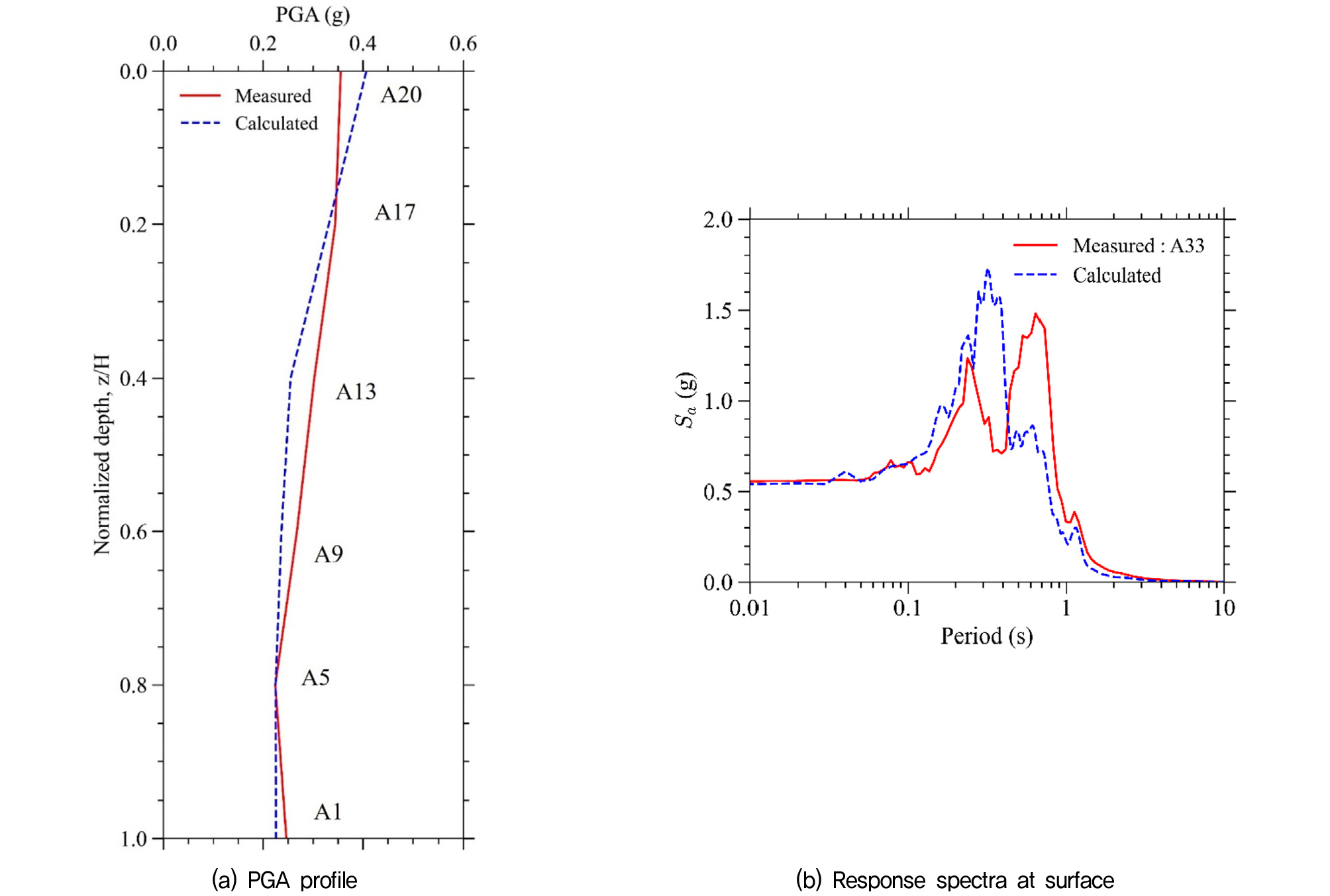
수치해석모델 지반영역에서의 자유장에서 계산된 결과와 원심모형실험에서의 측정값을 비교하여 본 연구의 수치해석모델을 검증하였다. 깊이에 대한 최대지반가속도 분포(Fig. 6a) 및 응답 스펙트럼(Fig. 6b)가 원심모형실험의 측정값과 유사하게 나타남을 확인하였다.
또한 구조물 벽체의 세가지 깊이에서의 최대지반가속도 분포 및 응답스펙트럼 또한 Fig. 7과 같이 수치해석 결과와 원심모형실험의 측정값이 유사하게 나타남을 확인하였다.
3. 베이스먼트 수치해석모델
3.1 베이스먼트 케이스 선정
본 연구에서 사례연구(Case study) 및 매개변수연구(Parametric study)를 수행하기 위해 가정한 베이스먼트 지하구조물은 Fig. 8과 같이 기반암 바로 위에 위치하고 있으며, 다양한 예시 구조물들의 기하학적 형상 및 세부적인 물성은 Table 5 및 Table 6과 같다. 구조물이 지반과 만나는 최외곽 벽의 두께는 일반적인 지하 구조물 또는 주요 건축물의 지하 구성요소 설계를 참고하여 깊이가 깊어짐에 따라 더 두꺼워지게끔 모델링하였는데, 이는 깊이가 깊어짐에 따라 증가하는 토압을 상쇄하기 위함이다(Wilbur and Mead, 1933; Lopez-Perez, 2013; Viswanath et al., 2003). 평면변형조건에서 수치해석을 수행하기 위해 Table 5의 등가 축 강성 및 휨 강성이 모델에 사용되었다.
Table 5.
Properties of basement structure
Table 6.
Study case matrix
| Case No. |
Embedment depth, H (m) |
Width, L (m) |
Aspect ratio, L/H |
Story height (m) |
Bay width (m) |
Flexibility ratio, F* |
| 1 | 20 | 16 | 0.8 | 4 | 8 | 3.58 |
| 2 | 20 | 40 | 2 | 4 | 8 | 4.76 |
| 3 | 20 | 80 | 4 | 4 | 8 | 5.88 |
구조물의 종횡비(L/H)가 토압에 미치는 영향을 조사하기 위해 다양한 구조물 높이(H)와 폭(L)을 가지는 예시 구조물을 선정하였다. 폭(L)은 12~20m, 높이(H)는 8~160m 범위에서 0.67, 0.8, 1.33, 2, 4, 8의 여섯 가지 L/H 값을 갖도록 선정하였다.
Table 6에서 계산된 유연성 비율(F)은 National Earthquake Hazards Reduction Program(NEHRP)에서 분류한 단단한 지반의 전단파속도 범위의 평균치인 Vs=250m/s에 대하여 계산한 값이며, 계산된 값의 범위는 2.87에서 6.22이다.
3.2 지반 프로파일 및 물성 선정
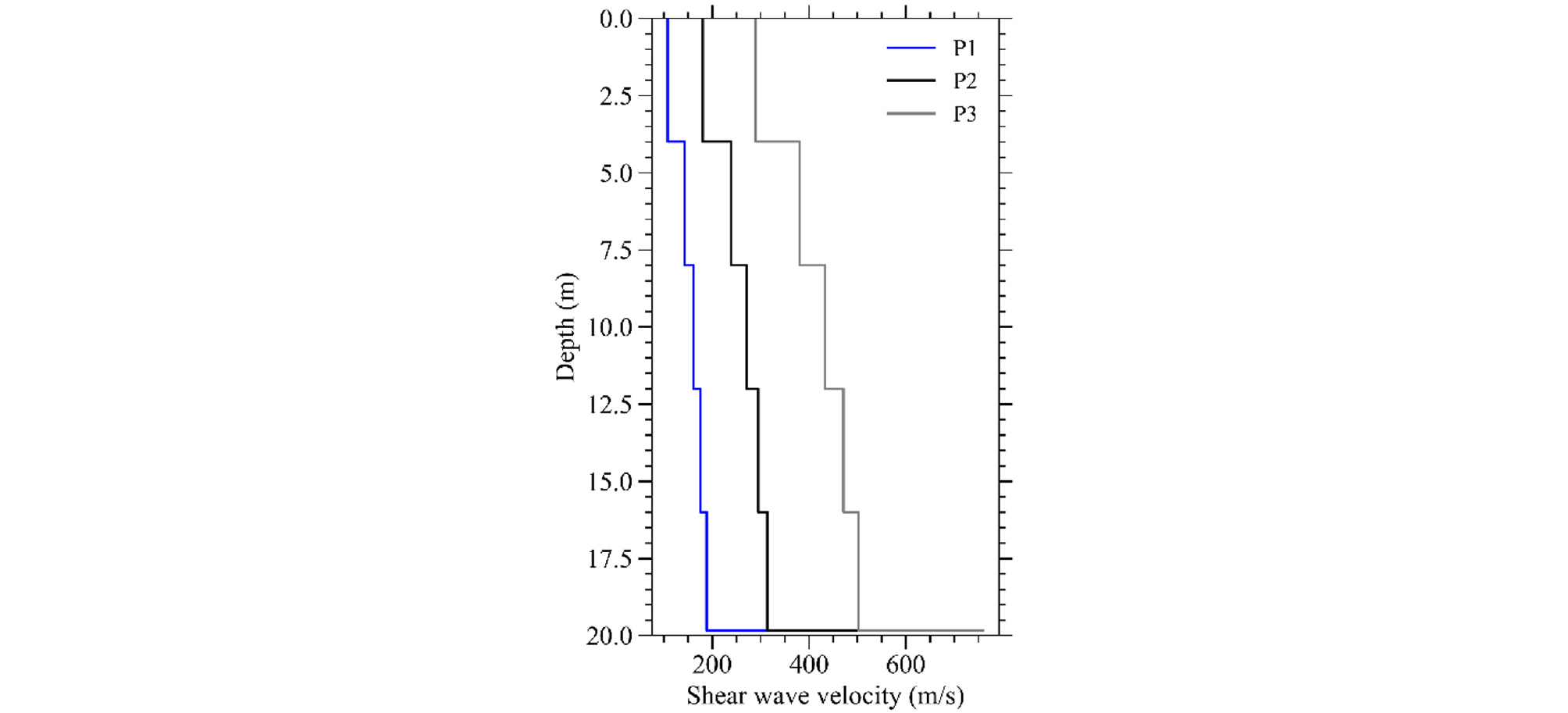
본 연구의 수치해석에서 사용된 예시 지반 3가지의 깊이에 따른 전단파속도 분포와 물성은 Table 7 및 Fig. 9와 같다. 각 지반의 Vs,soil의 범위는 150m/s, 250m/s, 400m/s 이며 토층 아래에는 760m/s의 전단파속도를 갖는 기반암이 있다. 이러한 지반은 한국에 많이 분포되어 있는 얕은 깊이 지반과 유사하게 볼 수 있다.
Table 7.
Soil profile matrix
| Embedment depth, H (m) | Profile | Vs,soil (m/s) | Vs,30 (m/s) |
| 20 | P1 | 150 | 205 |
| P2 | 200 | 265 | |
| P3 | 400 | 475 |
선정된 예시 지반들에 대해 먼저 1차원 지반응답해석을 수행하고, 2.3과 같은 과정을 거쳐 지반 각 층의 등가선형물성들을 계산하여 이를 수치해석모델에 적용하였다.
3.3 입력지진파 선정
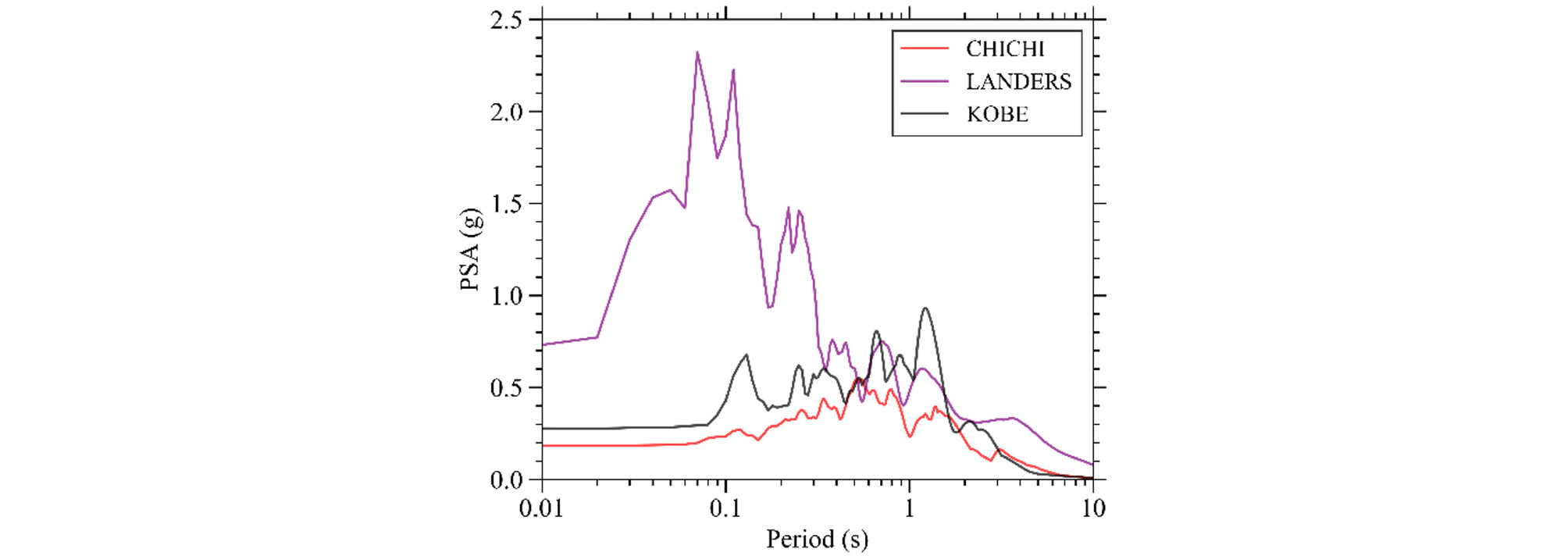
본 연구에서는 태평양지진공학센터(PEER)에서 제공하는 NGA-West2 데이터베이스로부터 Fig. 10과 같이 다양한 단주기 및 장주기 성분을 가지는 7개의 암반 기록 지진파(Outcrop motion)를 획득하여 사용하였다. 지진파의 관측소 및 기타 특성들은 Table 8과 같다. 선정된 지진파의 최대지반가속도의 범위는 0.15~0.74g이다.
4. 수치해석 결과
4.1 자유장 지반최대가속도
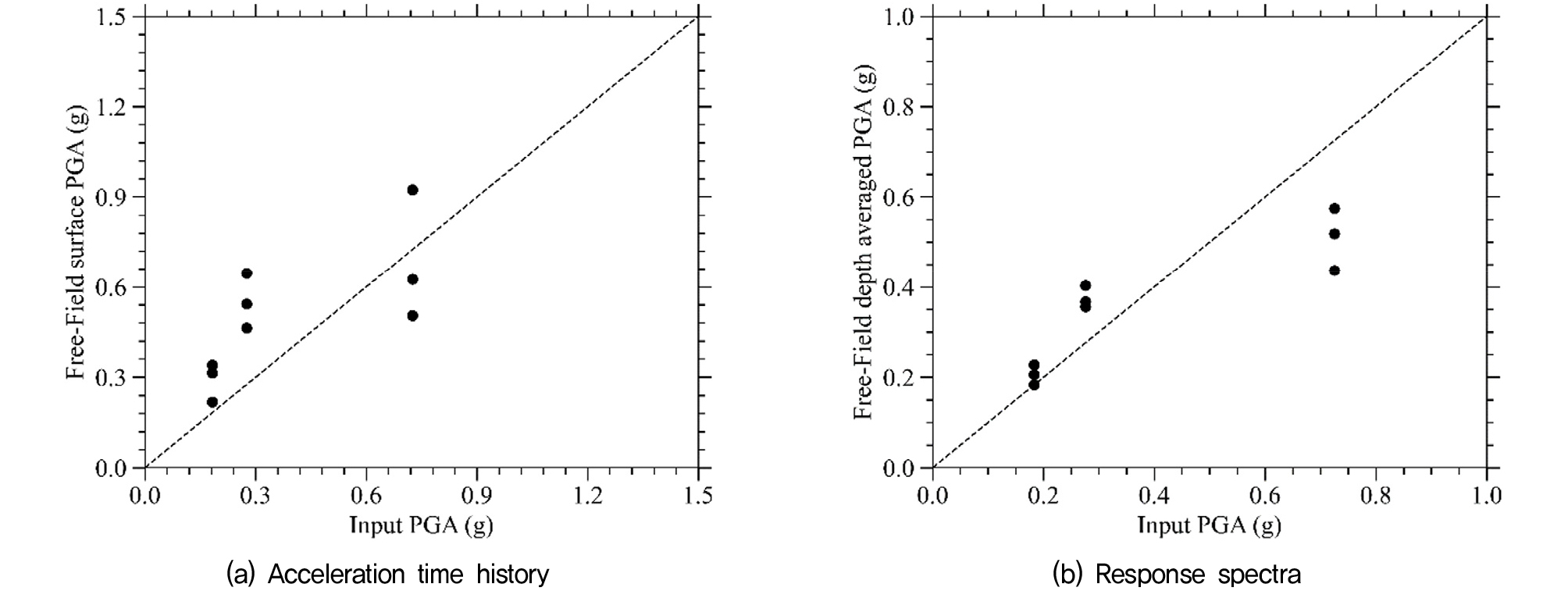
Fig. 11(a)와 11(b)는 입력지진파의 최대지반가속도에 대하여 자유장 영역 지표에서의 최대지반가속도 및 자유장 영역 각 깊이에서의 최대지반가속도의 평균치인 깊이 평균 최대지반가속도(kMHEA)를 나타낸 것이다. 기반암까지의 깊이가 깊지 않기 때문에 증폭이 잘 일어나는 것을 확인할 수 있으며 이때 지표에서의 최대지반가속도는 약 0.15~1.4g의 범위를 가진다.
4.2 래킹(Racking) 및 유연도(Flexibility) 비율
래킹(Racking) 변위는 구조물 하부에 대한 상부의 상대적인 측면 변위로 정의되는데, 주로 개착식 박스형 터널의 내진 설계에 사용되는 설계 파라미터로 터널의 종방향에 수직으로 전단파가 전파됨에 따라 야기되는 횡단면 형상의 왜곡 및 벽에서의 최대 모멘트를 평가한다(Anderson, 2008).
실제 적용에 있어서 박스형 구조의 래킹 변위는 Wang(1973)이 제안한 간소화된 방법을 근간으로 하는 NCHRP(National Cooperative Highway Research Program) 611 가이드라인의 방법을 사용하여 추정하는 경우가 많다(Anderson, 2008). 이때 래킹 비율(R)은 지반에 대한 구조물의 상대적 유연비(F)에 대한 경험식으로부터 추정된다.
본 연구에서도 구조물의 최대래킹변위(max|Δ structure|)에서 자유장 최대변위(max|Δ Free-field|)을 나누어 각 해석 케이스들의 래킹 비율을 계산하고, 자유장 지반에 대한 구조물의 유연성 비율(F) 또한 각 해석 케이스별로 NCHRP 611 가이드라인에 제시된 방법에 따라 다음과 같이 계산하였다.
여기서, L, H, Ks는 각각 지하 구조물의 폭, 높이, 래킹 강성(Racking stiffness)을 나타내며, Gm은 주변 지반의 평균전단탄성계수다. 예시 지반들에 입력된 각각의 지진파들의 영향을 모두 고려할 수 있게끔 먼저 지반 개별 층마다 유효 변형률에서의 등가선형 전단탄성계수(Gsec,i)를 계산하였고, 식 (6) 및 식 (7)을 사용하여 전체 깊이에 대하여 대표적인 평균전단탄성계수(Gm)를 계산하였다.
래킹강성(Ks)은 구조물에 대해 프레임 분석을 수행하여 계산하였다. 결과적으로 계산되는 유연비(F)의 범위에 따라 F<1 일 경우 구조물이 주변 지반에 비해 상대적으로 단단함을, F>1 일 경우 상대적으로 유연함을 나타낸다.
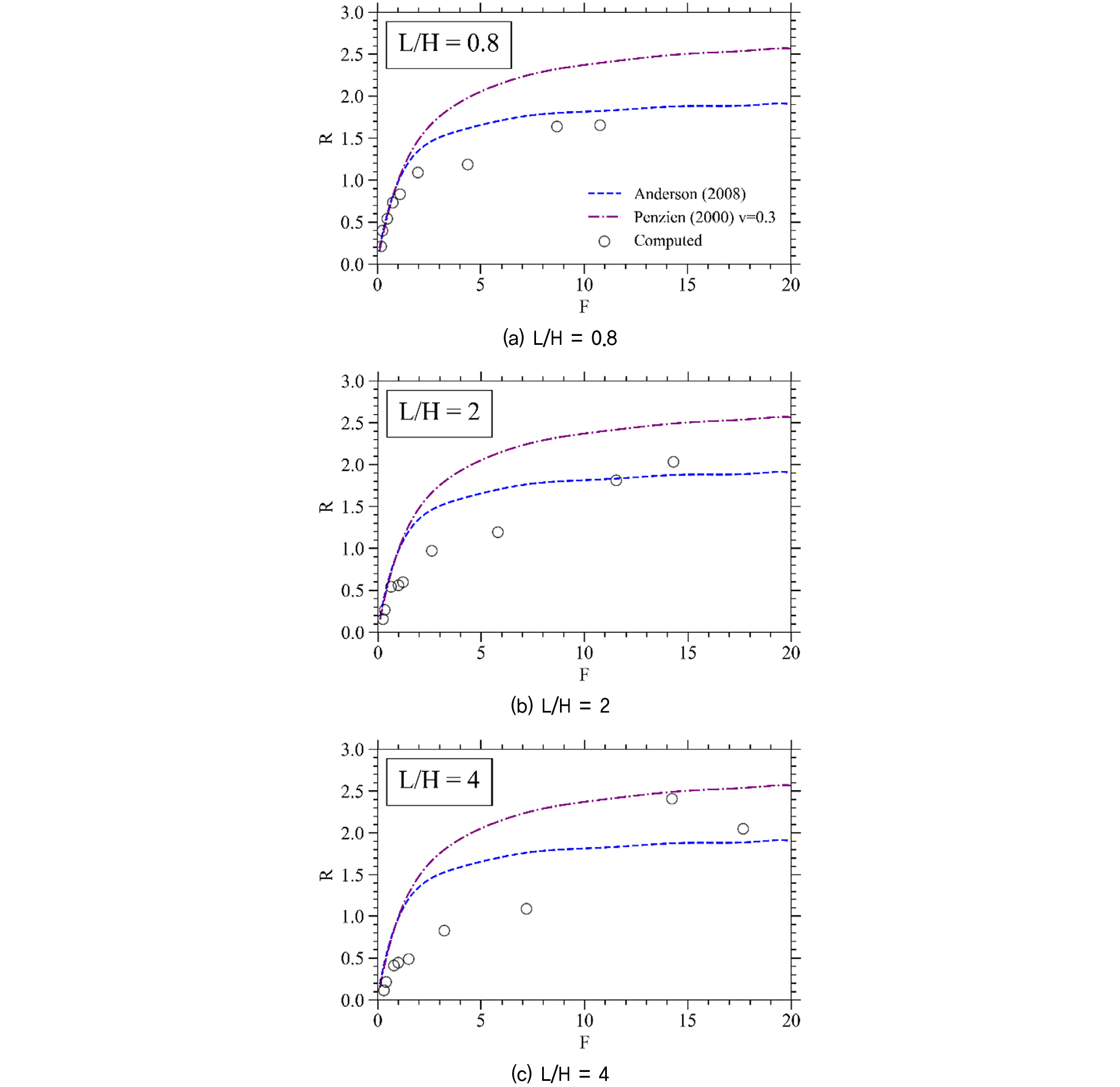
본 연구에서 수행한 총 27개 수치해석의 유연비와 래킹비율을 개착식 박스 터널에 대한 Anderson(2008)의 경험식 및 Penzien(2000)의 해석식을 Fig. 12에 함께 나타냈다. 해석 결과로부터 베이스먼트 지하구조물의 경우 박스 터널과 유사하지만 조금 다른 경향이 나타나는 것을 확인할 수 있었다. L/H가 0.8인 경우 Anderson(2008)의 경험식과 매우 유사한 경향을 나타냈으며, L/H가 커짐에 따라 래킹비율이 상대적으로 감소하는 경향을 보였다. 이러한 경향은 베이스먼트 지하구조물의 경우 터널과 달리 구조물 상부에 성토부가 없어 주변지반으로부터 전단력을 추가로 받지 않고, 그에 따라 큰 종횡비(L/H)를 가지는 구조물일수록 변형이 덜 일어나는 것으로 추측된다. 또 유연비에 대한 래킹비율의 분산도는 L/H가 증가함에 따라 증가하는 것을 확인하였다.
4.3 지진토압증분계수
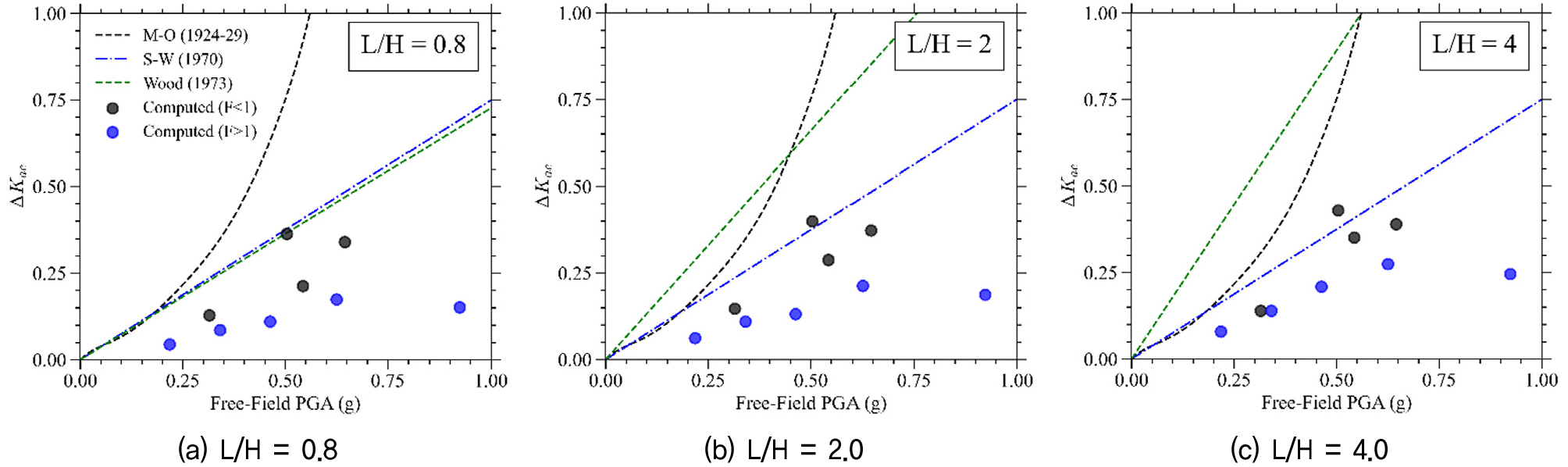
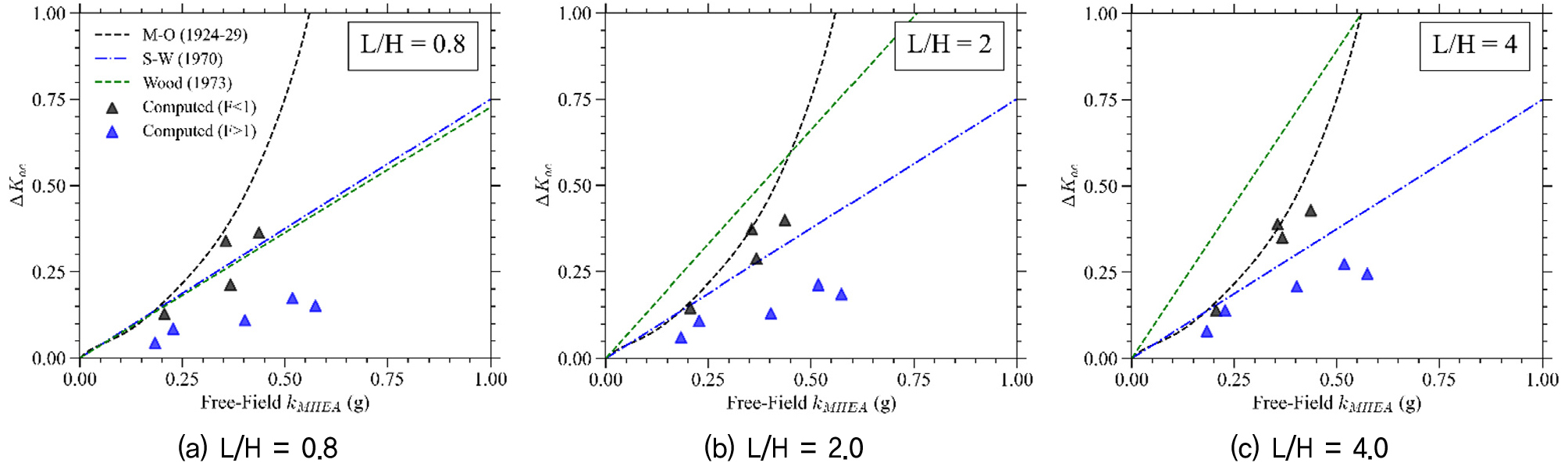
지진토압증분계수(∆Kae)는 지진 시 발생하는 토압의 증분 ∆Pae를 등가삼각형 면적(0.5γH2)으로 나누어 계산한다. 내진 설계 수행 시 ∆Kae는 중요한 설계 파라미터로서 자유장 지표에서의 최대지반가속도 및 깊이 평균 최대지반가속도(kMHEA)와 상관관계가 있다(Al Atik and Sitar, 2010; Wagner and Sitar, 2016; Hushmand et al., 2016a; Hashash, 2018; Bray et al., 1998). Fig. 13 및 Fig. 14에 수치해석결과로부터 계산된 지진토압증분계수(∆Kae)를 지표면의 최대지반가속도와 깊이 평균 최대지반가속도(kMHEA)에 대해 선행 연구들의 토압식과 함께 나타냈다.
구조물 종횡비(L/H)가 0.8, 2, 4에 대하여 구조물이 주변지반에 대해 상대적으로 단단한 상태인 F<1 그룹과 유연한 상태인 F>1의 그룹으로 나누어서 나타냈다. 이때 F>1의 그룹에서의 토압이 상대적으로 더 작게 나타나는 것을 확인하였으며, Wood(1973)의 연구에서와 같이 종횡비(L/H)가 증가함에 따라 ∆Kae가 증가하는 것을 확인할 수 있었다.
지표면에서의 최대지반가속도에 대한 ∆Kae의 경우 Fig. 13과 같이 모든 종횡비 조건에 대하여 F<1 및 F>1 그룹에서 모두 Seed and Whitman(1970) 토압식은 ∆Kae를 과대평가하였고, Mononobe and Matsuo(1929)와 Okabe(1924) 및 Wood(1973) 토압식은 더더욱 크게 ∆Kae를 과대평가하였다.
깊은 깊이를 가지는 지하 구조물의 경우, Wagner and Sitar(2016)는 깊이평균 최대지반가속도(kMHEA)를 사용하여 ∆Kae를 추정할 것을 권장하였다. Fig. 14를 보면, 모든 종횡비 조건에 대하여 F<1 그룹군에서 kMHEA가 0.4g보다 작을 때 Mononobe and Matsuo(1929)와 Okabe(1924)의 토압식이 ∆Kae 를 비교적 잘 예측함을 확인하였으며 kMHEA가 0.4g 이상일 경우 Seed and Whitman(1970) 토압식이 상대적으로 ∆Kae를 더 적절히 예측하는 것을 확인하였다.
또, 종횡비가 0.8, 2인 조건에 대하여 F>1 그룹군에서 Seed and Whitman(1970)은 ∆Kae를 크게 과대평가하였으며 종횡비 4에서 소폭 과대 추정하는 것을 확인하였다. Wood(1973) 토압식의 경우 전체적으로 ∆Kae를 과대평가한다.
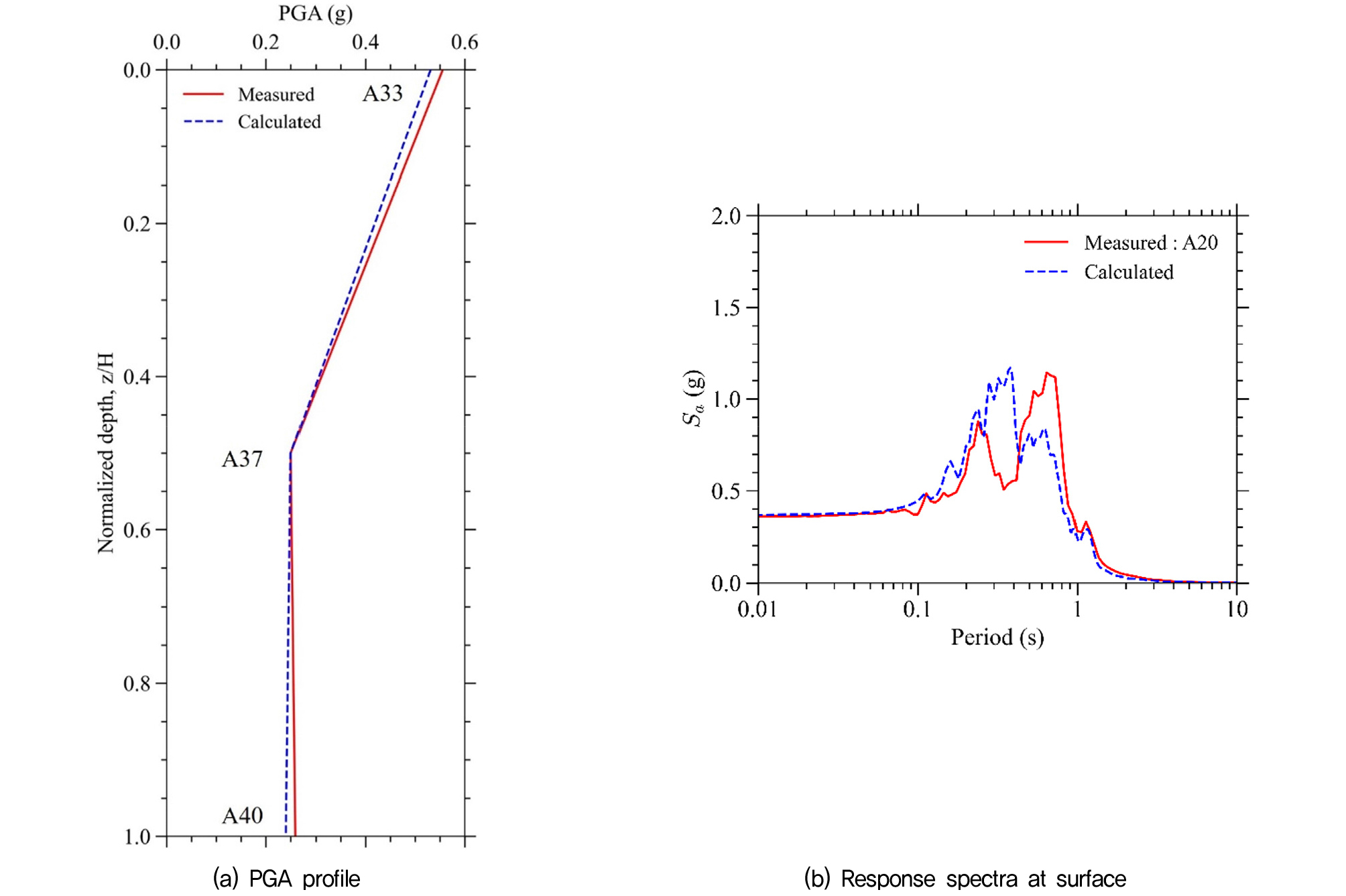
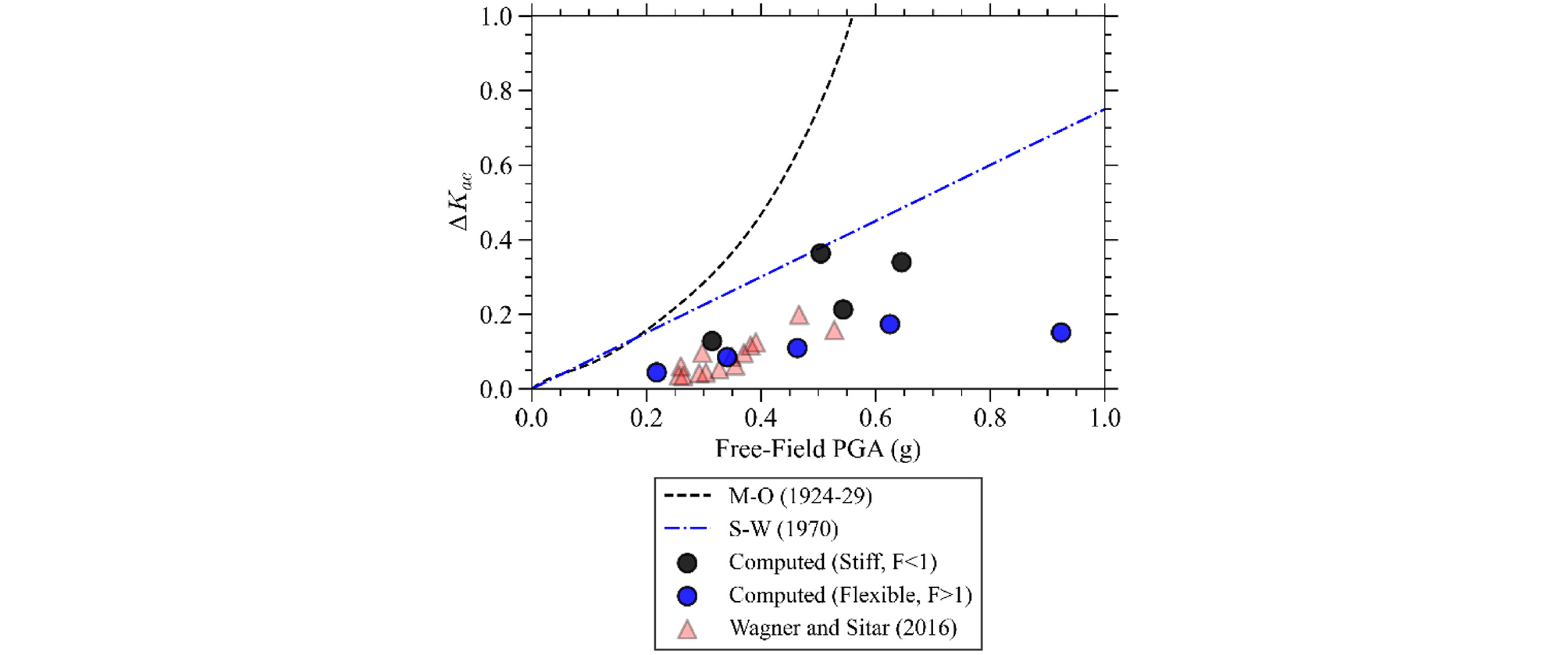
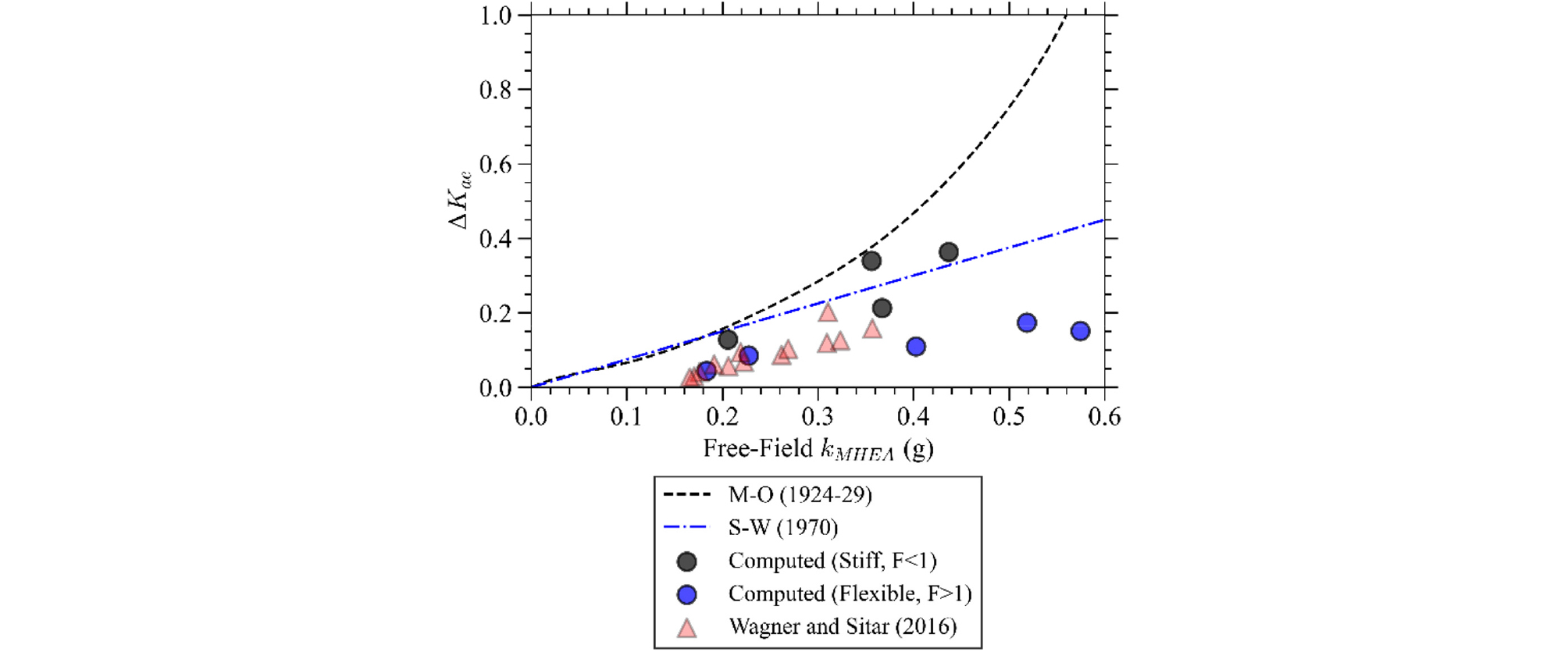
Wagner and Sitar(2016)의 원심모형실험은 가새로 보강된, 약 0.44의 종횡비(L/H)를 가지는 베이스먼트에 대해 수행되었다. 지표 최대지반가속도 및 깊이 평균 최대지반가속도에 대하여 원심모형실험 데이터 및 본 연구에서 0.8의 종횡비(L/H)를 가지는 구조물의 수치해석결과를 Fig. 15 및 Fig. 16에 함께 나타내었다.
5. 결 론
본 연구에서는 지하상가, 지하주차장 및 지하철역 등의 넓은 베이스먼트형 지하구조물에 대하여 선행연구들에서 중력식 옹벽, 캔틸레버식 옹벽 및 다양한 구조물 조건에 대해 제안된 토압식들의 적용성을 평가하고자 하였다. 이를 위해 먼저 본 연구에서 사용한 수치해석모델을 원심모형실험과 비교 검증하였고, 사례연구(Case study) 및 매개변수 연수(Parametric study)를 위해 예시 지반, 지진파, 그리고 다양한 유연성 비율(F) 및 종횡비(L/H)를 가지는 베이스먼트들을 선정하여 동적 수치해석을 수행하였다.
수치해석 결과, 지표면 및 깊이 평균 최대지반가속도(kMHEA)가 증가함에 따라 지진토압증분계수(∆Kae)도 증가하는 경향이 있음을 확인하였다. 특히, kMHEA에 대해 ∆Kae의 분산도가 더 작게 나타나, 추정의 일관성이 높아지는 것을 관찰하였다. 따라서 지진토압증분계수(∆Kae)를 추정할 때 지표면에서의 최대지반가속도보다 깊이 평균 최대지반가속도(kMHEA)를 고려하는 것이 더 적절하다.
지하 구조물의 동적 거동은 주로 유연성 비율(F)에 의해 결정된다. 개착식 박스형 터널에 대해 제안된 Wang(1993)의 유연비(F) 정의는 성토부가 없는 베이스먼트 지하구조물에도 적용될 수 있음을 확인하였다. 주변 지반에 비해 구조물이 상대적으로 단단한 F < 1의 상태인 경우 상대적으로 유연한 F > 1 상태일때에 비하여 동적토압이 크게 발생하는데, 이는 F가 클수록 큰 래킹 비율(R) 및 래킹 변위(Racking displacement)가 발생하여 결과적으로 동적토압이 감소하기 때문으로 보인다.
또, 구조물의 종횡비(L/H)가 높을수록 동적토압이 증가하는 것을 확인하였다. 이는 종횡비가큰 구조물일수록 래킹 비율(R) 및 래킹 변위(Racking displacement)가 감소하여 결과적으로 더 큰 동적토압을 받는 것으로 보인다.
선행 연구들의 토압식의 적용성의 경우, 모든 종횡비 조건에 대하여 F<1 그룹군에서 kMHEA가 0.4g보다 작을 때 Mononobe and Matsuo(1929)와 Okabe(1924)의 토압식이 ∆Kae를 비교적 잘 예측함을 확인하였으며 kMHEA가 0.4g 이상일 경우 Seed and Whitman(1970) 토압식이 상대적으로 ∆Kae를 더 적절히 예측하는 것을 확인하였다. 종횡비가 0.8, 2인 조건에 대하여 F > 1 그룹군에서 Seed and Whitman(1970)은 ∆Kae를 크게 과대평가하였으며 종횡비 4에서는 소폭 과대 추정하는 것을 확인하였다. Wood(1973) 토압식의 경우 전체적으로 ∆Kae를 과대평가하며, F < 1 그룹군의 경우 추정 ∆Kae 값에 1/3을 곱하여 사용하는 것이 적합하다고 판단된다.