1. 서 론
2. 침투해석(Seepage analysis)
2.1 수리구조물의 침투에 대한 안전성 검토
2.2 2차원 정상 침투
3. 투수계수의 공간적 변동성을 고려한 확률론적 침투해석
3.1 랜덤필드 모델
3.2 MCS에 의한 확률론적 해석
4. 취약도 곡선 작성
4.1 취약도 곡선
4.2 수리구조물의 기초지반을 통한 침투 취약도 곡선 작성
5. 차수벽체의 위치에 따른 취약도 곡선 작성
5.1 지반물성과 해석조건
5.2 확률론적 해석
5.3 취약도 곡선 작성
6. 결 론
1. 서 론
최근 기후변화로 인하여 수리구조물의 설계기준을 넘어서는 극한 홍수가 발생하면서 안전이 위협받고 있어 이에 대비하기 위한 기술개발이 요구되고 있다.
통상 수리구조물의 침투에 대한 안정성 평가는 결정론적 해석에 의한 안전율을 계산하여 경험에 의한 기준 안전율과 비교함으로써 수행되어왔다. 그러나 흙의 특성은 근원적으로 불확실성을 내포하고 있으므로 침투거동은 결정론적 특성보다는 확률론적 특성을 갖는다고 할 수 있다. 그뿐만 아니라, 안전율은 지반의 변동성 및 불확실성을 고려하지 못하므로 위험도(risk)에 대한 정량적이고 일관된 척도를 제공하지 못한다. 즉, 같은 안전율을 가진 지반일지라도 지반 물성의 변동 정도에 따라 다른 위험도를 주게 되므로 안전율에 의한 안정성 평가는 이론적 합리성이 부족한 측면이 있다(Cho, 2011). 안전율 기반의 결정론적 안정성 평가의 단점을 극복하고 지반의 불확실성과 변동성을 안정성평가에서 합리적으로 고려하기 위하여 확률론적 해석을 바탕으로 위험도를 정량적으로 해석, 평가하기 위한 시도가 지반공학 분야에도 도입되고 있다. 그러나 우리나라에서는 아직 안전율 기반의 결정론적 안정성 평가법이 침투 안정성 평가의 표준적인 절차로 적용되고 있다.
확률론적 해석법은 침투 안정성 해석과 설계에 투수계수의 공간적 변동성과 불확실성을 정량적으로 반영할 수 있으므로 수리구조물의 신뢰도와 취약도를 평가하는 데 유용하다. 지반 특성의 불확실성과 공간적 변동성을 고려한 확률론적 침투거동 연구가 여러 연구자에 의하여 연구가 수행되었다(Ahmed, 2012; Fenton and Griffiths, 1997; Griffiths and Fenton, 1998; Johari and Heydari, 2018; Srivastava et al., 2010).
특히 댐, 제방 등 홍수방어를 위한 기반시설의 효과적인 자산운용(asset management)을 위해서는 예상되는 하중에 대한 구조물의 성능을 폭넓게 평가할 필요가 있으며 이를 위해 취약도 곡선이 활용되고 있다(Simm and Tarrant, 2018; Rossi et al., 2021; USACE, 1996). 취약도 곡선은 가능한 범위의 하중 조건들에 대한 조건부 파괴확률을 나타내며 구조물의 성능은 취약도 곡선에 의해 특징지어질 수 있다(Kennedy et al., 1980; Tsompanakis et al., 2010). 취약도 곡선은 최대지반 가속도에 대하여 구조물의 성능을 평가하기 위해 지진공학 분야에서 사용되었다. 취약도 곡선은 노출될 가능성이 있는 하중 범위에 대하여 구조물의 신뢰도를 점이 아닌 함수의 형태로 나타내므로 점으로 표현되는 신뢰도 정보보다 구조물에 대한 폭넓은 신뢰도 정보를 제공할 수 있다(Cho, 2019). 따라서 최근에는 사면, 댐, 제방 등과 같은 지반구조물의 다양한 손상상태에 대한 위험도 평가 영역에서도 적용이 점차 증가하고 있다(USACE, 1996; Vorogushyn et al., 2009; Tsompanakis et al., 2010; Wu, 2015; Martinović et al., 2018).
국내에는 이수와 치수 등의 목적으로 설치 및 운영되고 있는 많은 수리 시설물이 존재한다. 특히, 2008년 4대강 사업으로 한강, 금강, 영산강, 낙동강을 중심으로 다수의 보 시설물이 설치되었으며 이후 누수, 파이핑, 양압력 등 보 시설물의 안전에 대한 지속적인 문제가 제기되어 왔다. 이러한 수리구조물의 유지관리를 위해서는 현재 및 미래의 운영 중에 발생 가능한 수위에 대한 성능을 평가해야 한다.
수리구조물의 하부를 통한 침투를 조절함으로써 성능을 확보하기 위하여 차수벽체(cutoff wall)가 지반에 설치된다. 부적절한 차수벽체의 설치는 기초지반의 파이핑에 대한 안정성을 저해할 뿐 아니라 과도한 침투량으로 인하여 수리구조물의 건설로 인한 편익을 감소시킨다. 즉, 큰 유출동수경사(exit gradient)에 의하여 유발되는 파이핑(piping)은 구조물의 안정성을 위협하고 궁극적으로는 구조물이 파괴에 도달하는 원인이 되며 과도한 침투량 발생은 발전, 용수확보 등의 수리구조물 축조로 인한 가용 수량 확보를 저해한다. 따라서 구조물의 안정성을 확보하고 최대 편익을 확보하기 위한 차수벽체의 최적 위치를 결정하는 것이 중요하다.
본 연구에서는 확률론적 해석을 바탕으로 취약도 곡선을 결정하는 절차를 제시하고 침투조절을 위하여 설치되는 차수벽체의 위치에 따른 수리구조물의 취약도 곡선을 작성하였다. 이를 위해 수위를 변경하면서 Monte Carlo Simulation(MCS)에 의한 확률론적 침투해석을 수행하였으며 침투가 발생하는 기초지반에서의 투수계수의 불확실성과 공간적 변동성을 고려하였다.
2. 침투해석(Seepage analysis)
2.1 수리구조물의 침투에 대한 안전성 검토
댐이나 보와 같은 수리구조물의 설계, 시공 및 유지관리를 위해서 기초지반을 통한 침투로 인한 안정성을 검토해야 한다. 이를 위해 기초지반을 통한 침투유량, 침투수가 구조물과 지반의 안정성에 미치는 영향을 검토하고 검토 결과에 따라 침투조절 대책을 수립해야 한다.
허용 침투량은 저수의 목적 및 안전성에 따라 다르므로 명확하게 규정되어 있지는 않으나 어느 한도를 넘어서면 보일링이나 파이핑 등으로 인하여 파괴가 발생하게 되므로 신중하게 검토한 후 대책을 수립해야 한다. 더불어 저수 효율 측면에서 허용 침투량을 규정하여 관리하기도 한다.
침투수가 지반의 안정성에 미치는 영향을 검토하기 위하여 파이핑과 보일링(boiling)에 대한 안정성 평가, 침투해석을 통한 구조물 기초의 안정해석 등을 수행한다. 파이핑과 보일링을 방지하고 침투수 자체를 감소시키고 양압력을 감소시켜 안정성을 확보하기 위해서는 침투조절 공법의 적용이 필요하다. 최적의 침투조절 공법을 선택하기 위해서는 다양한 대안 적용에 따른 침투해석을 통한 최적화가 필요하다. 파이핑에 대한 검토는 한계동수경사 ic를 구하여 보일링 현상의 발생 가능성을 검토하여 안전여부를 판정한다. 분사현상에 대한 저항력은 소성지수가 큰 재료일수록 큰 경향이 있으며 점착력이 없는 세립자의 ic는 0.5~0.8로 본다. 침투해석에 의하여 산출한 동수경사가 한계동수경사의 1/2이하가 되도록 해야 한다(KWRA, 2011).
2.2 2차원 정상 침투
흙 속의 서로 연결되어 있는 간극을 통한 흐름이 층류인 경우에 지반의 임의 점에서의 유속 v와 동수경사 i 사이에는 다음과 같이 Darcy의 법칙이 관계가 성립한다.
여기서, k는 투수계수(m/sec)이다.
유체를 비압축성으로 가정하면 지반을 통한 2차원 정상상태 흐름(steady state flow)은 연속방정식과 Darcy의 법칙으로부터 다음과 같은 미분방정식으로 표현된다.
여기서, H는 전수두, kx, ky는 x와 y 방향의 투수계수이다.
식 (2)를 풀면 전수두가 구해지고 이로부터 동수경사, 간극수압, 유량을 계산할 수 있다. 해를 구하기 위한 여러 방법이 있지만, 해석단면의 기하학적 형상, 지반조건의 변동성, 복잡한 경계조건 등을 효과적으로 고려하기 위하여 유한요소법, 유한차분법 등의 수치해석 기법이 주로 활용되고 있다. 본 연구에서는 유한요소법을 이용하여 2차원 정상상태 침투해석을 수행하였다.
3. 투수계수의 공간적 변동성을 고려한 확률론적 침투해석
3.1 랜덤필드 모델
흙은 조성 성분, 퇴적상황, 응력이력 등으로 인하여 균질한 층에서도 위치에 따라 변동성을 갖는 재료이며 이러한 공간적인 변동성은 지반의 불확실성을 유발하는 본질적인 원인이다(Lacasse와 Nadim, 1996).
지반물성의 공간적 변동성은 랜덤필드 모델의 이론적 틀에서 상관구조(correlation structure)에 의해 설명될 수 있다(Vanmarcke, 1983). 지반의 특성이 강한 상관성을 나타내는 공간적인 범위를 나타내기 위해 자기상관거리(autocorrelation distance)를 사용한다. 자기상관거리가 클수록 지반의 물성이 넓은 공간적 범위에 걸쳐서 강한 상관성을 나타내어 지층 내에서 점진적인 변화를 보이는 것을 의미하며 작은 자기상관거리는 지반의 변동폭이 크게 나타나는 것을 의미한다(Cho, 2011).
Gaussian 랜덤필드는 평균 μ, 분산 σ2 및 자기상관함수 ρ(x, x')에 의해서 정의되며 본 연구에서는 식 (4)와 같은 지수형태의 상관함수를 사용하였다.
여기서, lh, lv는 각각 수평 및 연직 방향의 자기상관거리이다.
침투와 관련된 지반 특성인 투수계수의 공간적 변동성을 나타내기 위해서 랜덤필드로 모델링해야 한다. 침투해석을 위해 사용하는 유한요소법은 불연속적인 특성을 가지므로 지반물성의 랜덤필드를 유한 개의 랜덤변수들로 표현해야 하며 이러한 과정을 랜덤필드의 이산화(discretization)라 한다. 본 연구에서는 포화투수계수의 2차원 랜덤필드를 이산화하기 위해서 Karhunen-Loève 전개법을 사용한다. 랜덤필드 이산화를 위한 자세한 절차는 Cho(2011)에 의하여 기술되었다.
3.2 MCS에 의한 확률론적 해석
취약도 곡선은 구조물이 노출되는 하중 범위에 걸쳐 구조물의 성능에 대한 정량적 정보를 제공하며 지배적인 하중변수에 대한 파괴확률의 관계로 표현된다. 이때 파괴는 반드시 구조물의 완전한 붕괴(collapse)를 의미하는 것은 아니고 요구되는 성능을 만족시키지 못하는 상태를 의미하므로 파괴확률은 주어진 한계상태를 초과할 확률을 계산하여 구한다.
확률론적 침투해석의 문제는 흙의 투수 특성을 나타내는 랜덤변수들의 벡터 X로 정식화되며, 설계변수의 공간에서 안전한 상태와 파괴상태의 경계를 정의하는 한계상태함수 g(X)는 이들 랜덤변수들에 의해 정의된다(Cho, 2011). 이때 파괴확률은 파괴영역에 대하여 수행되는 다차원의 적분식으로 표현된다.
여기서, fX는 랜덤벡터 X의 결합확률밀도함수(joint probability density function)이다.
MCS는 확률분포 및 상관 구조와 일치하는 일련의 랜덤벡터를 생성하고, 생성된 각 표본에 대해 한계상태함수를 계산함으로써 식 (1)의 정확한 해를 구하는 유일한 보편적 방법이다. 이 과정을 충분한 횟수 반복하여 파괴확률을 추정할 수 있다.
침투 문제에서 파이핑, 양압력, 침투량 등과 관련된 여러 파괴모드(failure mode)에 따라 파괴를 정의하는 한계상태함수는 다음과 같이 정의될 수 있다.
여기서, scrit는 파괴를 유발하는 임계 침투 물리량이며 s는 해석에 의해 계산된 침투 물리량이다.
4. 취약도 곡선 작성
4.1 취약도 곡선
전통적인 결정론적 해석법에서 구조물은 파괴하중(failure load)에서 안전(파괴확률 0)과 파괴(파괴확률 1.0) 둘 중 하나로 구분되므로 확률론적 관점에서 안전성 판단에 불연속적인 특성을 갖는다. 그러나 실제로 구조물은 가해지는 하중 수준에 따라 연속적인 파괴확률을 나타내며 결정론적 해석법에서 파괴를 유발하는 파괴하중에서 파괴확률 1.0에 도달하지 않을 수도 있다.
Kennedy et al.(1980)은 취약도 곡선을 원자력 발전소 구성 요소의 파괴 빈도와 지진의 최대 지반가속도 사이의 확률적 관계로 정의했다. 보다 일반적으로, 취약도 곡선은 시설물 또는 구성 요소가 환경적인 자극을 나타내는 지표의 함수로 명확하게 정의되는 한계상태에 도달하거나 초과할 확률을 표현하는 관계로 정의될 수 있다(Porter, 2018). 현재 취약도 곡선은 다양한 형태의 기반시설물에 적용되고 있다. 이 곡선은 잠재적 손상에 대한 예측을 제공하며 기반시설물의 총 위험도를 평가하는 데 사용된다. 따라서 취약도 곡선은 재해 경감을 위한 비상사태 대비에 필수적인 재난 시 의사 결정 도구로 사용될 수 있다(Cho, 2019).
취약도 곡선은 발생한 피해의 관찰, 해석 또는 전문가의 판단과 같은 다양한 접근법을 사용하여 도출할 수 있다(Kennedy and Ravindra, 1984). 본 연구에서는 해석적 접근법으로 취약도 곡선을 작성하였다.
주어진 하중강도 LI=h에서 구조물에 대한 취약도(fragility) HF는 MCS의 결과로부터 구한다. 수리구조물의 침투 안정성을 지배하는 주요 하중 변수는 침투를 유발하는 구조물 상·하류의 수두차이므로 상·하류의 수두차와 연관된 구조물 상류의 수위 h에 따른 취약도 곡선을 작성하였다.
식 (6)의 함수는 일정 범위에 걸쳐 주어진 하중 조건에 대한 조건부 누적확률이다. 취약도 곡선은 수위에 따른 구조물의 저항을 나타내지만, 특정 수위 발생의 확률이 고려되지는 않는다. 따라서 최종 파괴확률을 계산하기 위해서는 작성된 취약도 곡선을 수위에 대한 확률모델과 결합해야 한다(Vorogushyn et al., 2009).
4.2 수리구조물의 기초지반을 통한 침투 취약도 곡선 작성
0≤s<+∞이고 평균 μ와 표준편차 σ를 갖는 연속확률변수 s가 대수정규분포를 따르면 lns는 평균 과 표준편차 를 갖는 정규분포를 따르게 되며 누적분포함수(Cumulative Distribution Function, CDF)는 다음과 같이 표현된다.
여기서, Φ는 표준정규분포의 누적분포함수이다.
투수계수의 공간적 변동성을 고려한 수리구조물의 기초지반에서의 침투에 대한 MCS 결과로부터 얻어진 유출동수경사, 양압력의 합력, 침투수량의 확률분포는 대수정규분포로 나타낼 수 있다. 유출동수경사, 양압력의 합력, 침투수량을 대수정규분포를 따르는 확률변수 s로 고려하면 파괴확률은 다음과 같이 계산된다.
수위 h가 변하면 유출동수경사, 양압력의 합력, 침투수량의 평균 μ와 표준편차 σ가 달라지므로 이에따른 파괴확률 Pf를 식 (8)로부터 계산하면 수위에 따른 파괴확률의 관계인 취약도 곡선을 작성할 수 있다.
5. 차수벽체의 위치에 따른 취약도 곡선 작성
투수계수는 지반의 침투거동과 관련된 물리량들을 계산하기 위해 사용되므로 투수계수의 공간적 변동성과 관련된 불확실성은 해석을 통하여 계산되는 간극수압, 침투량, 동수경사 등의 불확실성을 야기한다. 따라서 본 연구에서는 투수계수 k를 랜덤필드로 고려하여 수리 구조물의 기초지반을 통한 침투거동을 해석하였으며, 침투조절을 위한 차수벽의 설치 유무 및 위치에 따른 취약도 곡선을 작성하여 그 거동을 연구하였다.
5.1 지반물성과 해석조건
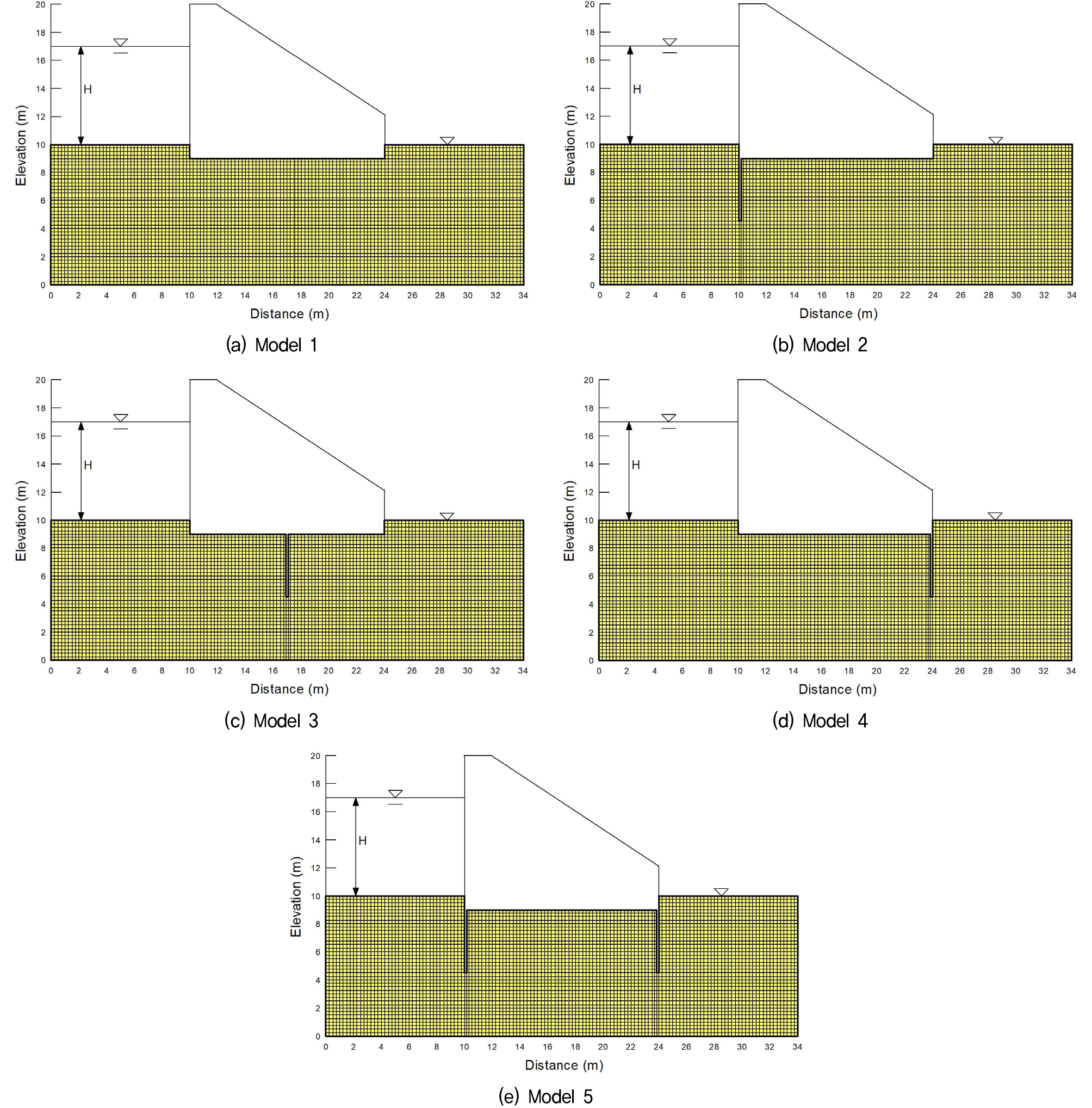
본 연구에서는 투수계수의 공간적 변동성을 고려할 수 있도록 침투 유한요소해석 프로그램을 개발하여 사용하였다. 차수벽체의 위치에 따른 침투거동을 연구하기 위해 Fig. 1과 같이 하부 지반에 설치되는 차수벽체에 따라 5개의 해석모델을 구성하였다. 대상 시설물의 기하학적 형상(보의 상·하류 방향의 기초 길이에 대한 최고수위의 비 등)에 따라 침투거동이 영향을 받으나, 본 연구에서는 침투거동을 명확하게 파악하기 위하여 Fig. 1과 같은 단순한 형상을 선정하였다. 침투해석을 위하여 사용된 지반의 물성값은 실트질 모래를 기준으로 투수계수의 변동계수 및 자기상관거리의 영향을 고려하기 위하여 Cho(2011)가 기본 해석 대상으로 선정한 Table 1을 사용하였다.
Table 1.
Input parameters used for seepage analysis (lognormal distribution)
| Mean μ (m/sec) | COV (=σ/μ) | Autocorrelation distance (m) | |
| Hydraulic conductivity, k | 1×10-5 | 0.5 | lh=20, lv=2 |
일반적으로 Fig. 1과 같은 수리구조물의 침투에 대한 안정성을 검토하기 위해서는 침투수가 집중되는 구조물에 인접한 하류 유출면에서의 동수경사인 최대 유출동수경사, 기초지반을 통해 발생하는 침투량, 구조물의 바닥에 작용하는 양압력(uplift pressure)을 계산할 필요가 있다. 침투로 인하여 구조물의 바닥에 작용하는 양압력의 합력은 구조물의 바닥을 따라 사다리꼴 규칙(trapezoidal rule)을 사용하여 작용하는 수압을 적분하여 구할 수 있다(Cho(2011)).
5.2 확률론적 해석
수리구조물의 하부 기초지반에서 투수계수의 공간적 변동성을 고려하기 위하여 투수계수를 랜덤필드로 고려하여 침투해석을 수행하였다. 이를 위해 Table 1에 제시된 투수계수의 통계학적 자료를 입력으로 사용하였다. 확률론적으로 변수 k의 평균과 표준편차로 정의되는 대수정규분포를 따른다고 가정하였다. MCS로부터 확률론적 침투 거동을 구하기 위해 10,000회의 랜덤필드를 생성하였으며 하나의 생성된 랜덤필드는 가능한 하나의 투수계수의 분포를 나타낸다. 수위를 변경하면서 각각 10,000회의 생성된 랜덤필드에 대하여 침투해석을 수행함으로써 침투거동과 관련된 물리량들인 유출동수경사(exit gradient), 침투율(flow rate, 기초지반을 통한 단위 시간당 침투량), 양압력의 합력(uplift force)의 확률분포를 구할 수 있고 식 (8)로부터 파괴모드별로 수위에 따른 파괴확률을 구하였다. 사용된 유한요소망과 경계조건은 Fig. 1과 같다.
수리구조물의 수위 h는 기초지반의 높이인 10m로부터 최대 수리구조물의 상단 높이 20m까지 변동할 수 있다. 본 연구에서는 해석 대상으로 lh=20m, lv=2m, COVk=0.5인 조건을 고려하였으나 추후 투수계수의 변동계수 및 자기상관거리가 수리구조물의 취약도 곡선에 미치는 영향을 연구할 필요가 있다.
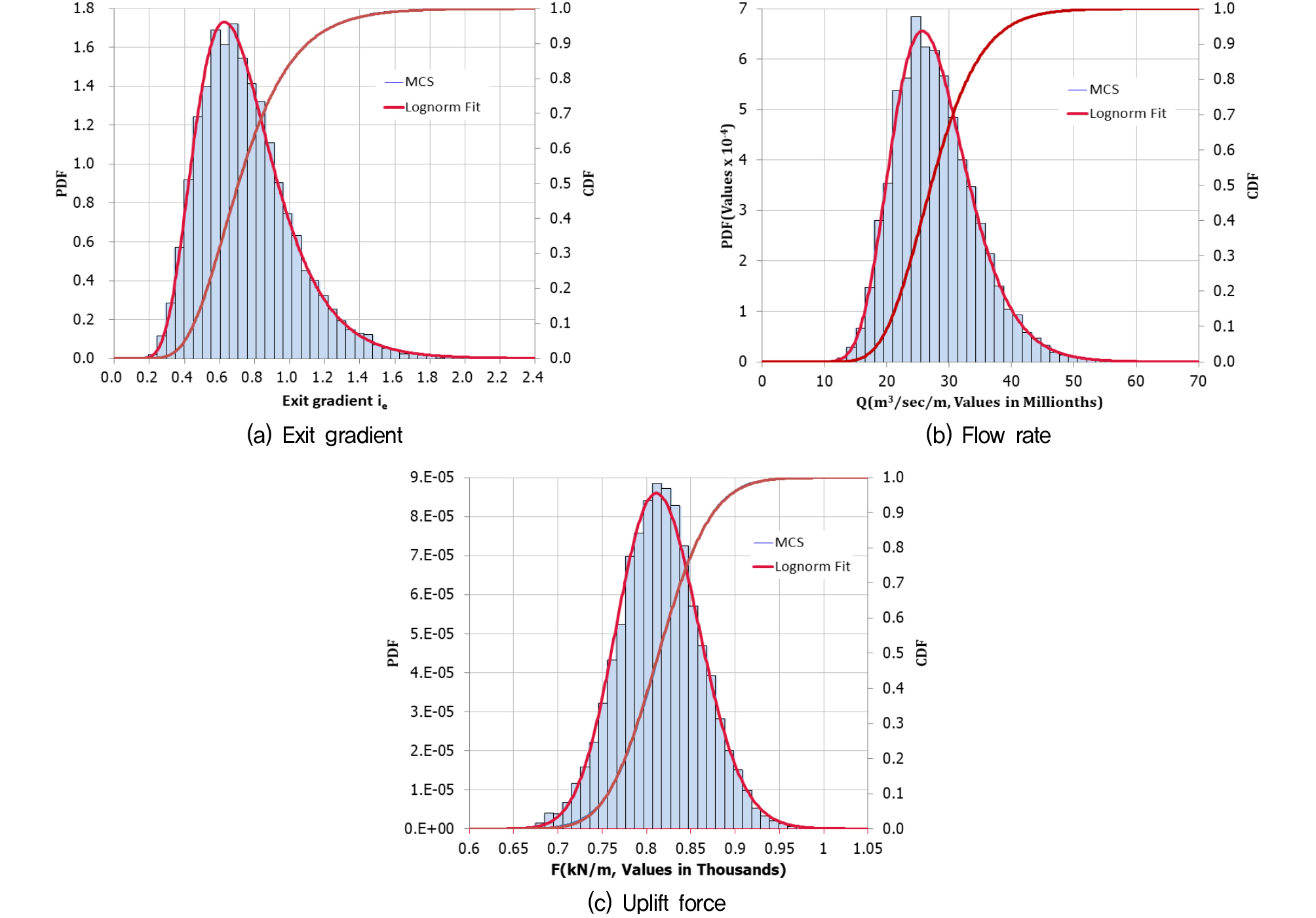
Fig. 2는 Model 3에서 h=20m인 경우의 유출동수경사, 양압력의 합력, 지반을 통한 시간당 침투량의 MCS 결과와 대수정규분포로 곡선 맞춤한 결과를 나타낸 것으로 대수정규분포에 의해 확률론적 침투거동을 잘 표현할 수 있음을 보여준다.
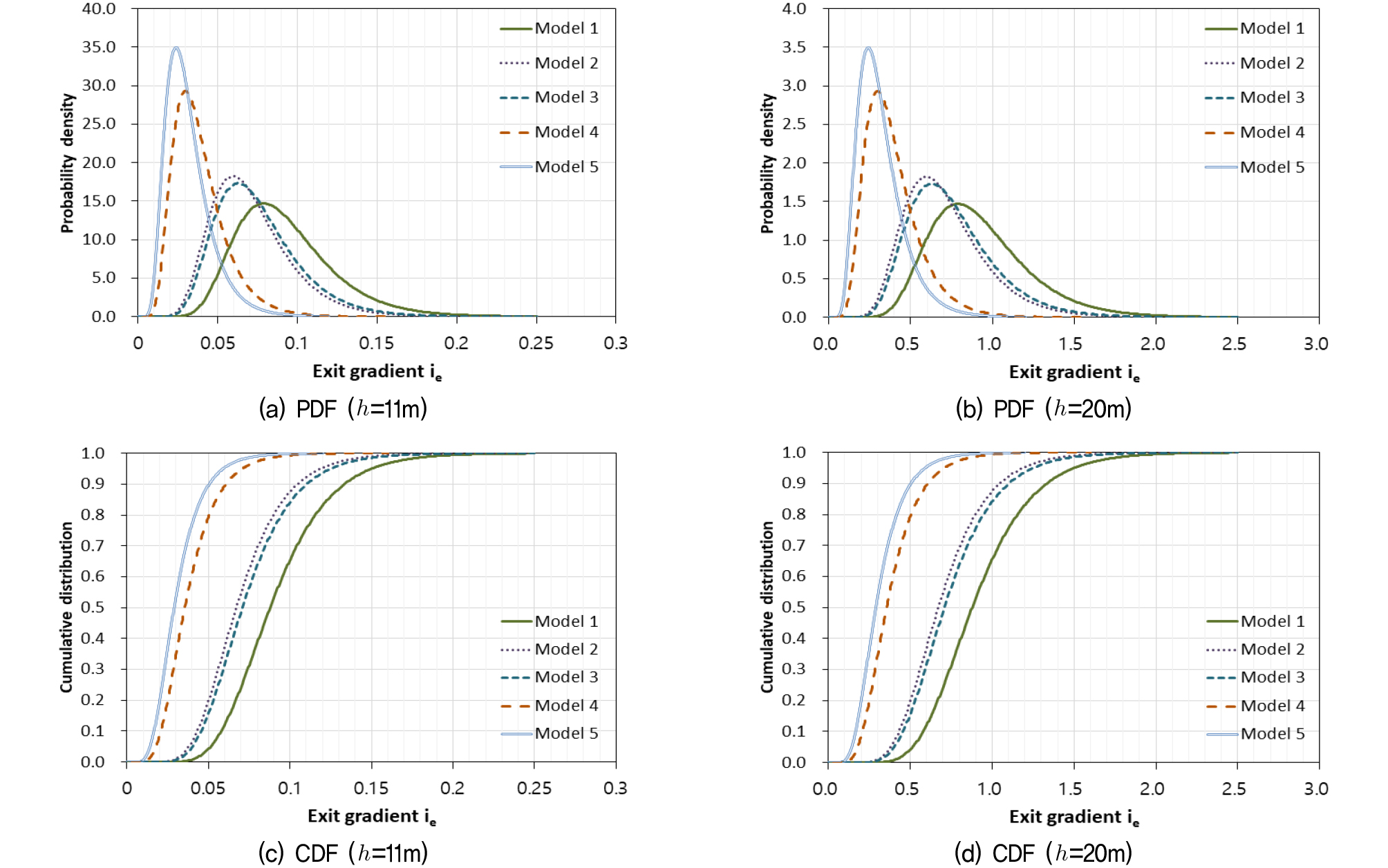
Fig. 3은 수위가 11m와 20m일 때 MCS에 의해 구한 유출동수경사의 확률밀도함수(Probability Density Function, PDF)와 누적확률분포(Cumulative Distribution Function, CDF)를 나타내고 있다. 확률밀도함수는 대수정규분포로 나타낼 수 있으며 점진적으로 감소하는 긴 우측 꼬리를 갖는 확률분포 형태, 즉 큰 값들이 왼쪽에 많아 양의 왜도(skewness)를 갖는다. 수위가 11m와 20m인 경우의 확률분포를 살펴보면 수위가 높아짐에 따라 발생하는 유출동수경사가 커지므로 횡축의 유출동수경사 분포범위가 달라질 뿐 확률분포의 기본 형태는 수위 변동에 상관없이 같은 모습을 나타냄을 알 수 있다. 확률밀도는 상·하류부 2곳에 차수벽이 설치된 Model 5에서 가장 높고 좁은 분포를 보이고 차수벽이 미설치된 Model 1에서 가장 낮고 넓은 분포형태를 보임을 알 수 있다. 하나의 차수벽이 설치될 때에는 하류에 설치된 Model 4가 좁은 분포를 나타냈고 상류부(Model 2)와 중간부(Model 3)의 경우는 유사한 분포를 나타냈다. 확률밀도함수의 모양에 따라 누적확률분포가 결정되므로 상·하류부 2곳에 차수벽이 설치된 경우가 곡선의 기울기가 가장 급하고 차수벽이 미설치된 경우가 가장 완만하게 나타났다(Figs. 3(c) and (d)).
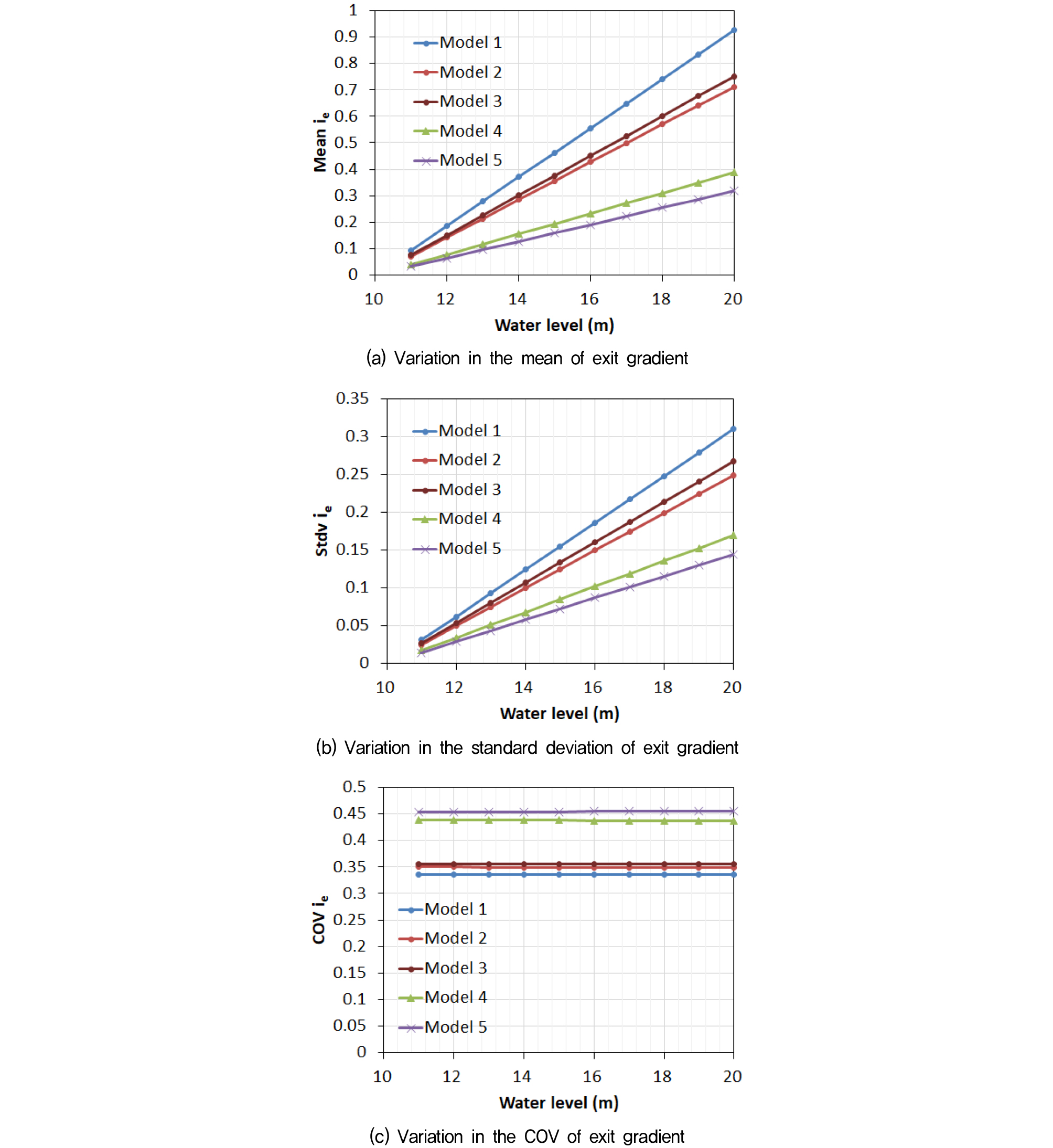
Fig. 4(a)는 PDF로부터 평가된 유출동수경사의 평균, 표준편차, 변동계수를 수위에 따라 나타낸 것이다. 확률론적 해석으로 평가된 유출동수경사의 평균(Fig. 4(a))은 수위가 증가할수록 비례하여 커지며 모든 수위에서 차수벽이 없는 Model 1에서 가장 큰 값을 보였고 차수벽이 상·하류에 모두 존재하는 Model 5에서 가장 작은 값을 보였다. 하나의 차수벽이 존재할 때에는 중간부, 상류부, 하류부 순으로 평균값은 작아졌고 중간부, 상류부의 경우 차이가 크지 않아 유출동수경사의 평균적 관점에서는 하류부에 설치되는 경우가 가장 효과적임을 알 수 있다. Fig. 4(b)는 표준편차를 나타낸 것으로 평균 유출경사가 큰 경우가 표준편차도 크게 나타났으며 이는 Fig. 3에서 PDF 곡선이 오른쪽으로 이동할수록 넓게 분포하는 모양으로 나타난다. 해석모델에 따른 유출동수경사의 흩어진 정도를 비교하기 위해서 표준편차를 사용하려면 평균의 영향을 제거해야 하므로 Fig. 4(c)과 같이 평균과 표준편차로부터 변동계수를 계산하였다. 변동계수는 Model 1, Model 2, Model 3, Model 4, Model 5 순으로 증가하였다. 특히, 하류부에 차수벽이 설치되는 Model 4, Model 5에서 투수계수의 변동성으로 인한 유출동수경사의 변동성이 크게 나타난다고 평가할 수 있다. 모든 해석모델에서 수위에 따른 변동계수의 변화는 없어 일정한 값을 나타내었다.
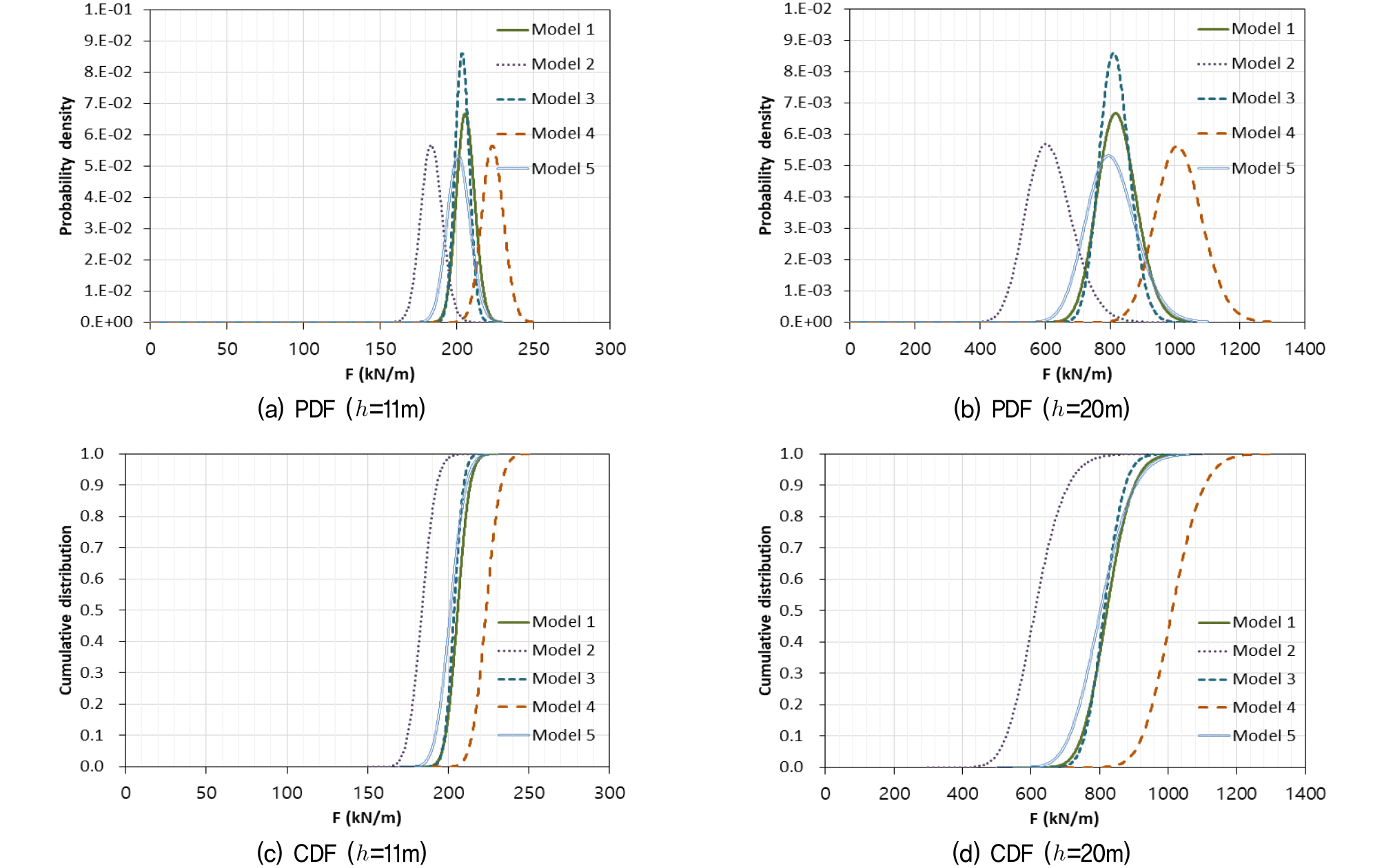
Fig. 5는 수위가 11m와 20m일 때 MCS에 의해 구한 구조물 하부에 작용하는 양압력의 합력의 확률밀도함수와 누적확률분포를 나타낸다. 수위가 11m와 20m일 때 확률분포의 형태는 유사하나 수위가 높아짐에 따라 발생하는 양압력이 증가하므로 합력의 범위만 달라진다. 확률밀도함수의 형태는 대체로 대칭을 이루고 좁은 범위에 분포한다. 중간부에 차수벽이 있는 Model 3에서 PDF가 가장 뾰족한 모습을 나타내고 있어 누적확률분포곡선의 기울기가 가장 급하게 나타나고 있다.
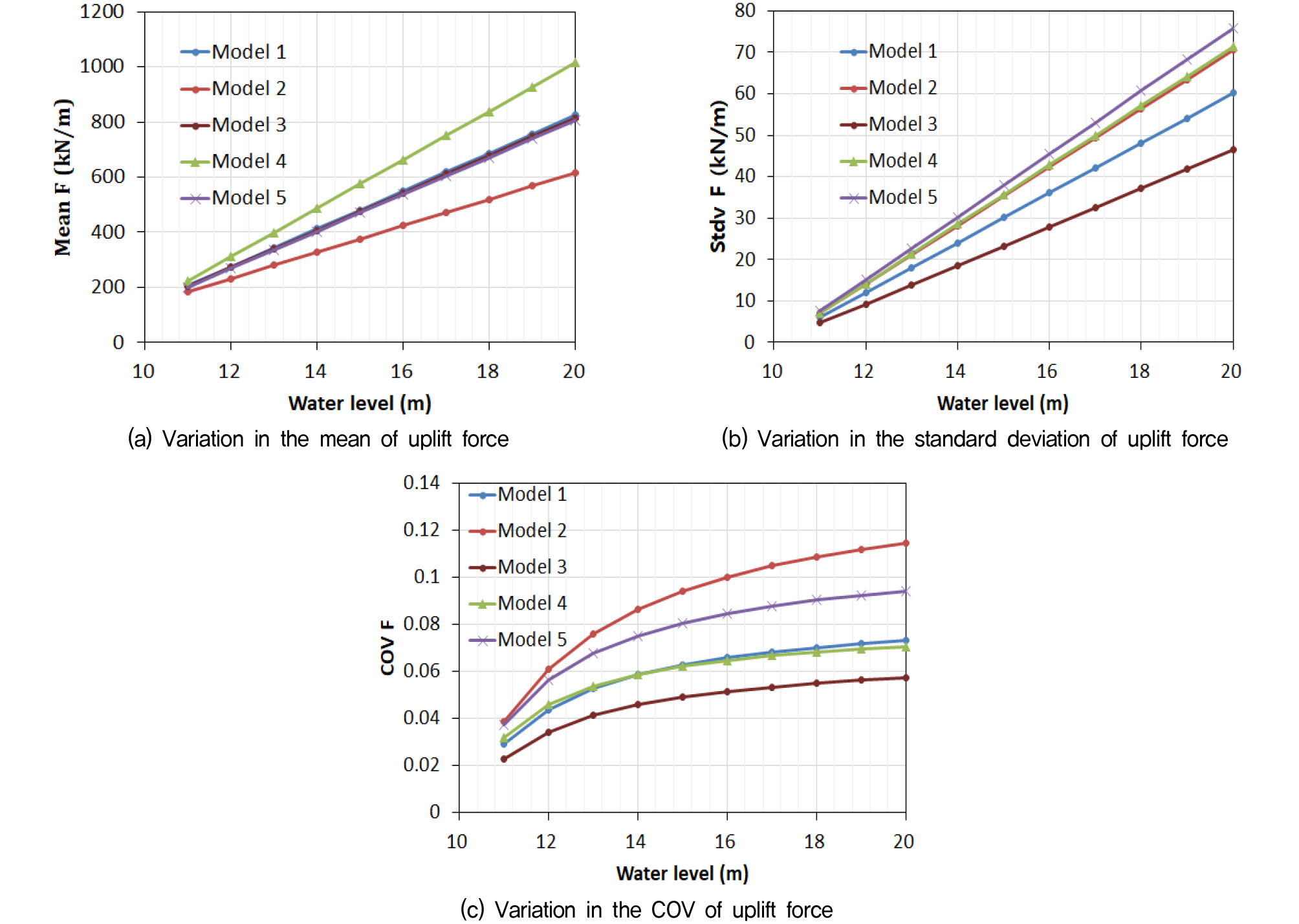
Fig. 6(a)는 PDF로부터 평가된 양압력 합력의 평균을 나타내며 모든 수위에 대하여 상류부에 설치한 Model 2에서 가장 작은 값을 나타냈고 하류부에 설치한 Model 4에서 가장 큰 값을 나타냈다. 나머지 상·하류부 동시 설치, 중간부에 설치, 차수벽이 없는 경우의 값들은 거의 같았다. 따라서 양압력의 평균적 관점에서는 차수벽을 상류부에 설치하는 Model 2가 가장 효과적이었다. Fig. 6(b)는 PDF로부터 평가된 표준편차를 나타내며 Fig. 6(c)는 변동계수를 나타낸다. 변동계수는 대체로 매우 작은 값을 나타내나 수위가 높아질수록 커지는 경향을 보이며, 수위가 높아질수록 해석모델에 따른 차이가 벌어지는 결과를 보인다. 차수벽이 중간부에 설치된 Model 3에서 변동계수가 제일 작고 상류에 설치된 Model 2에서 가장 크게 나타났다.
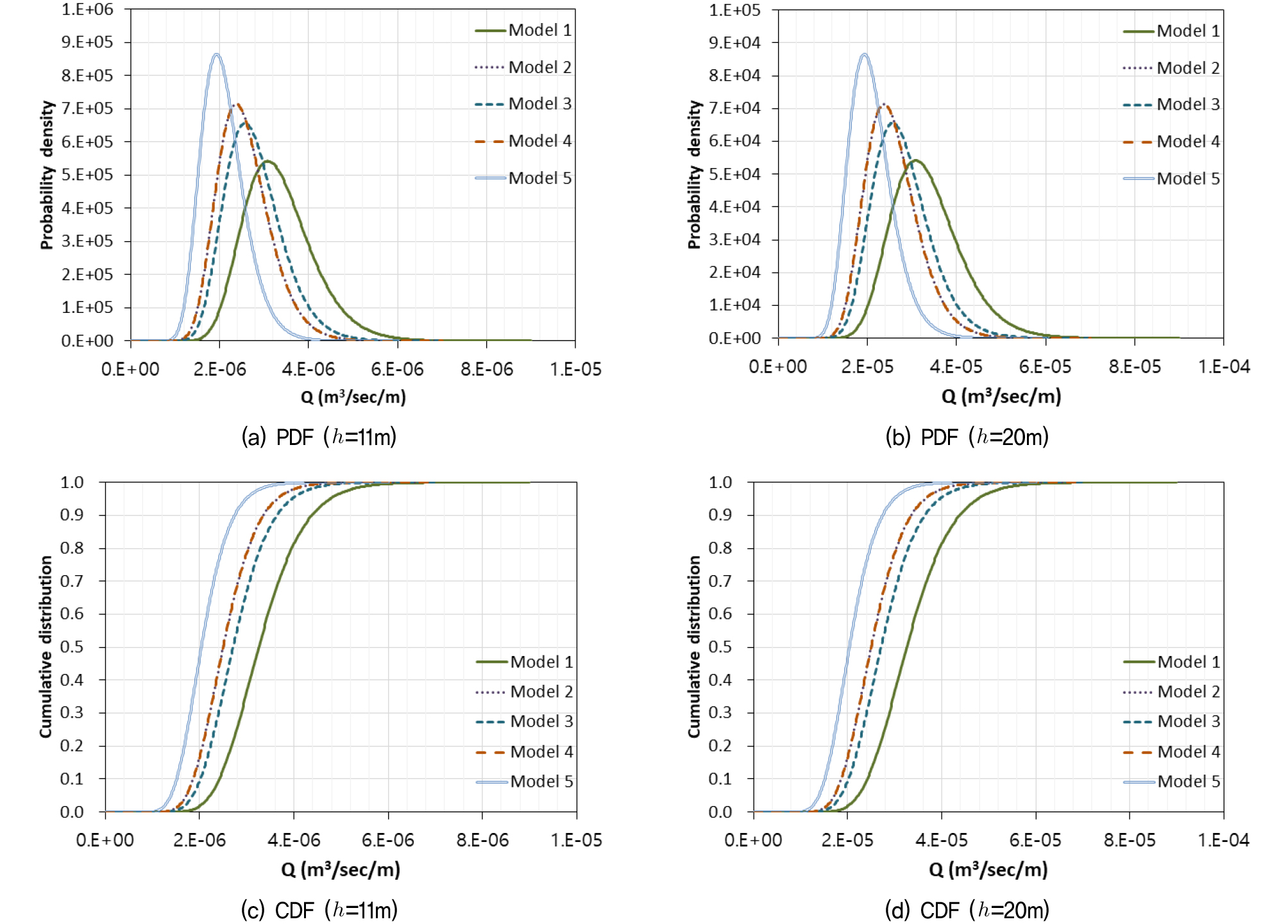
Fig. 7은 수위가 11m와 20m일 때 구조물 하부의 기초지반을 통하여 흐르는 침투율의 확률밀도함수와 누적확률분포를 MCS에 의해 구한 것이다. 마찬가지로 수위 11m와 20m일 때 확률분포의 형태는 유사하나 수위가 높아짐에 따라 발생하는 단위 시간당 침투량이 증가하므로 분포범위만 달라진다. 침투율의 확률밀도함수는 대수정규분포로 나타낼 수 있으며 유출동수경사의 경우와 같이 양의 왜도를 갖는다.
상·하류 양쪽에 차수벽이 있는 Model 5의 PDF가 가장 뾰족한 모습을 나타냈고 차수벽이 미설치된 Model 1의 경우가 가장 낮고 넓은 모양을 나타냈다. 특히, 상류부에 설치된 Model 2와 하류부에 차수벽이 설치된 Model 4의 경우는 완전하게 일치하는 PDF와 CDF를 나타냈다.
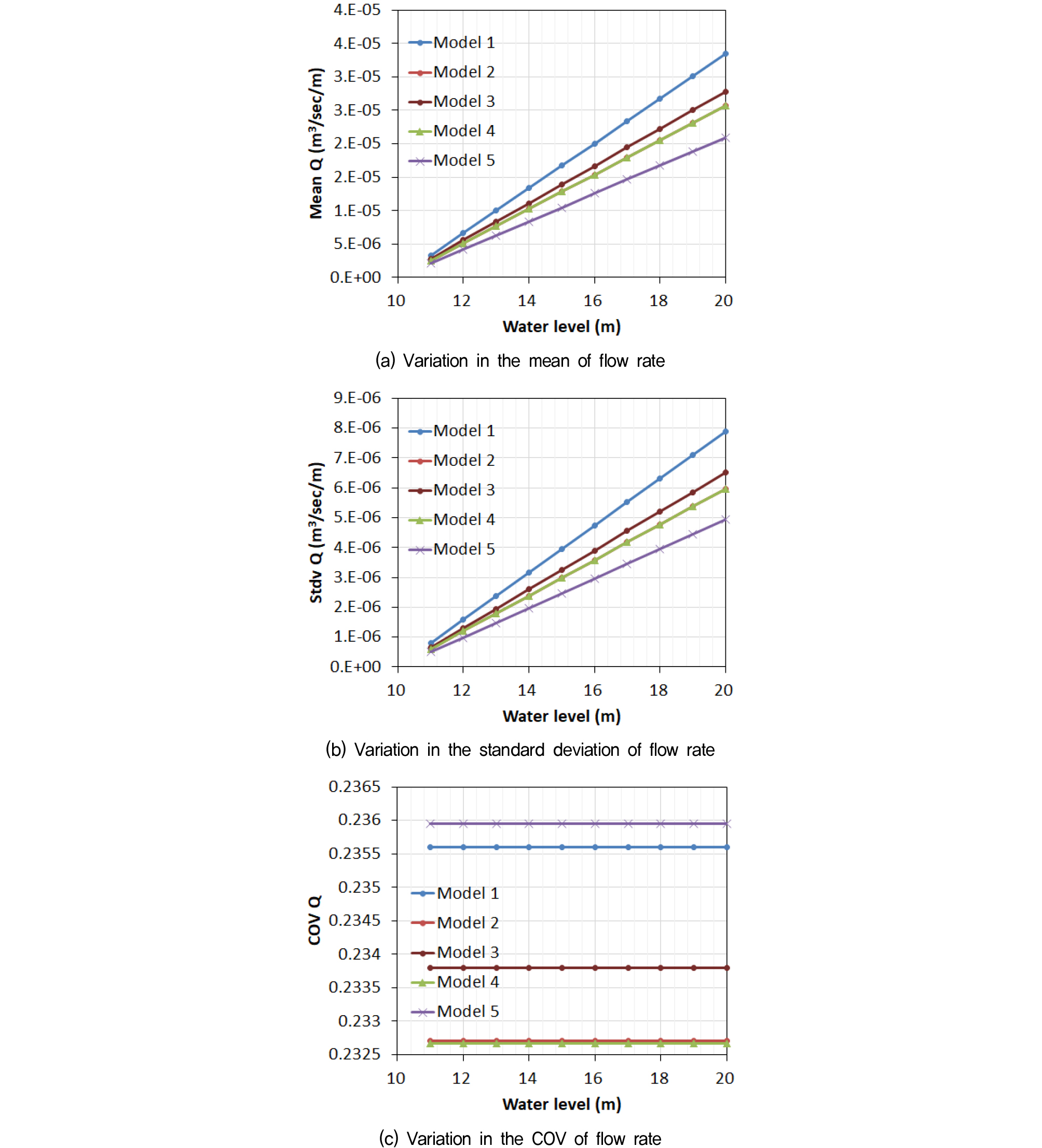
Fig. 8(a)는 PDF로부터 평가된 침투율의 평균을 나타내며 수위가 증가할수록 비례하여 증가하였다. 모든 수위에서 차수벽이 없는 Model 1에서 가장 큰 값을 보였고 차수벽이 상·하류에 모두 존재하는 Model 5에서 가장 작은 값을 보였다. 하나의 차수벽이 존재할 때에는 중간부에 있는 경우가 큰 유량을 보였고 상류부에 설치된 Model 2와 하류부에 설치된 Model 4의 경우에는 같은 값을 나타냈다. 침투량의 평균적 관점에서 차수벽이 상·하류부에 설치된 Model 5의 경우가 효과적임을 알 수 있다. Fig. 8(b)는 PDF로부터 평가된 침투율의 표준편차를 나타내며 평균값의 경향과 유사한 거동을 보였다. Fig. 8(c)의 변동계수는 유출동수경사의 경우보다는 작고 양압력의 경우보다는 큰 값을 나타냈으며 수위에 상관없이 일정한 값을 나타내고 있다. Model 2와 Model 3에서 변동계수가 제일 작고 Model 5의 경우가 가장 크게 나타났으나 Model에 따른 값의 차이는 실질적으로 미미하였다.
5.3 취약도 곡선 작성
취약도 곡선은 수위를 바꿔가며 해당하는 파괴확률을 구하여 수위에 따른 파괴확률의 관계를 나타낸 것이다. 원칙적으로 파괴확률은 MCS 시행 중 파괴 여부를 판단하기 위해서 한계상태함수의 값을 계산하여 전체횟수 중 파괴가 발생한 해석 횟수의 비로 계산할 수 있다. 그러나 MCS로부터 직접 파괴확률을 구하기 위해서는 많은 시행 횟수가 필요하고 취약도 곡선은 수위에 따라 파괴확률을 반복적으로 구해야 하므로 직접 MCS의 적용은 취약도 곡선 작성에 과다한 시간의 소모를 유발한다. 따라서, 본 연구에서는 MCS로부터 추정한 PDF로부터 파괴확률을 계산하는 방법을 사용하였다.
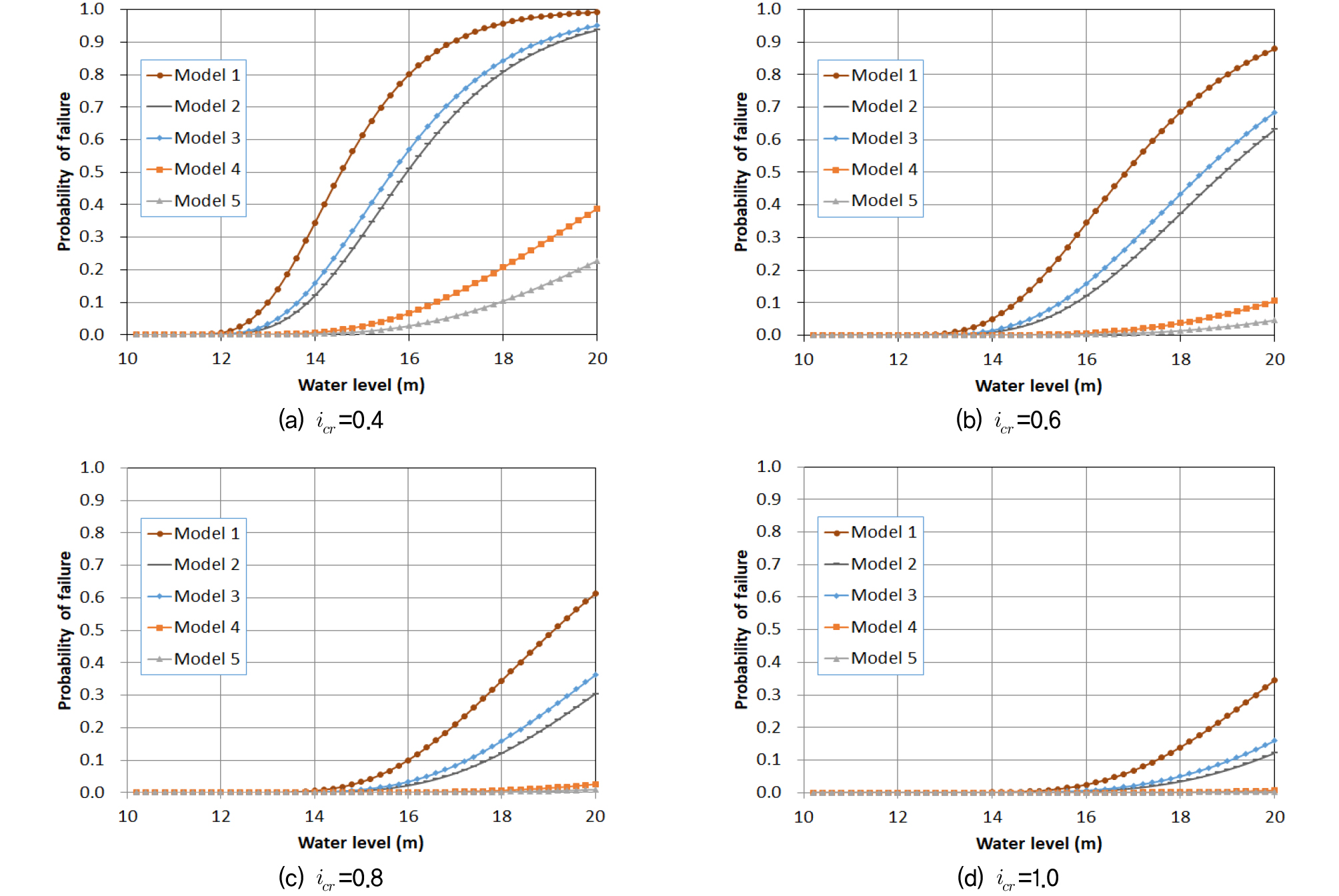
Fig. 9는 수위를 바꿔가며 수행한 MCS에 의해 구한 유출동수경사의 확률분포로부터 계산한 구조물 하부 지반의 유출부에서의 취약도 곡선이다. 취약도 곡선은 한계상태를 계산하는 데 사용된 한계동수경사의 값을 변경하면서 구하였다. 모든 한계동수경사 값에 대하여 임의의 수위에 대응하는 파괴확률은 차수벽이 설치되지 않은 Model 1에서 가장 크고, 상·하류 2곳에 차수벽이 설치된 Model 5의 경우가 가장 작았다. 하나의 차수벽이 설치된 경우는 중간부, 상류부, 하류부 설치 순으로 파괴확률이 낮아졌다. 취약도 곡선으로부터 수위가 증가함에 따라 구조물의 파괴확률이 어떻게 변화하는지에 대한 정보를 얻을 수 있으므로 안전관리나 위험도 평가에 활용할 수 있다. 예를 들어 Fig. 9(a)에서 차수벽이 미설치된 경우는 저수위에서는 수위가 증가해도 파괴확률의 변화가 미미하다가 수위가 약 12m를 넘어서면 수위에 따라 파괴확률이 급격하게 증가하고 구조물 상단 높이인 20m에 가까워질수록 증가율이 줄어들게 되며 최대수위 20m에 접근하면 파괴확률은 1.0에 거의 도달하게 된다. 이에 비해 차수벽이 설치되면 파괴확률이 급격하게 증가하게 되는 수위가 높아지고 높이 증가에 따른 파괴확률 증가 기울기도 감소하게 된다. 한계동수경사가 1.0인 Fig. 9(d)에서 차수벽이 하류부에 설치되거나 상·하류부 2곳에 설치되면 수위가 구조물 상단인 20m에 도달하여도 파이핑에 대한 파괴확률은 매우 작게 유지됨을 알 수 있다.
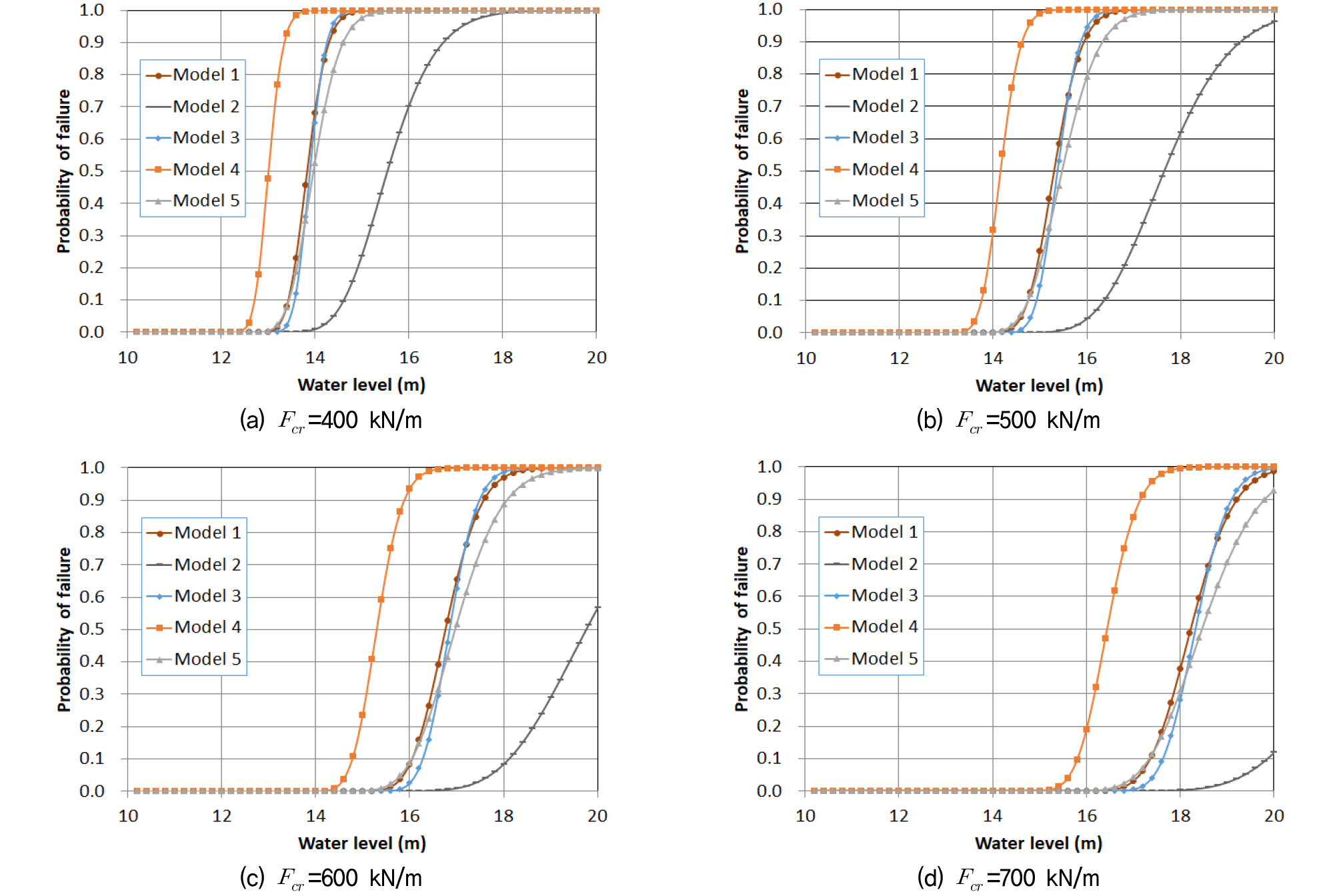
Fig. 10은 한계상태를 계산하는 데 사용된 한계양압력의 값을 변화시키면서 각각 취약도 곡선을 구한 것이다. 하류부에 차수벽이 설치되었을 때(Model 4)에 임의의 수위에 대한 파괴확률이 제일 높고 상류에 설치된 경우(Model 2)가 가장 작았다. 특히, Fig. 10(a)에서 Model 1, 3, 4, 5에서는 곡선의 기울기가 매우 급하여 일정 수위를 넘어서면 파괴확률이 급격하게 증가하여 작은 수위 변동에도 파괴확률 1.0에 도달하였다. 이에 비해 차수벽이 상류부에 설치된 경우(Model 2)에는 파괴확률이 상승하게 되는 임계수위도 높고 곡선의 기울기가 다른 해석모델들에 비해 완만하여 상류 측에 차수벽을 설치하는 것이 양압력에 의한 파괴확률을 감소시켜 위험도를 관리함에 매우 유용함을 알 수 있다.
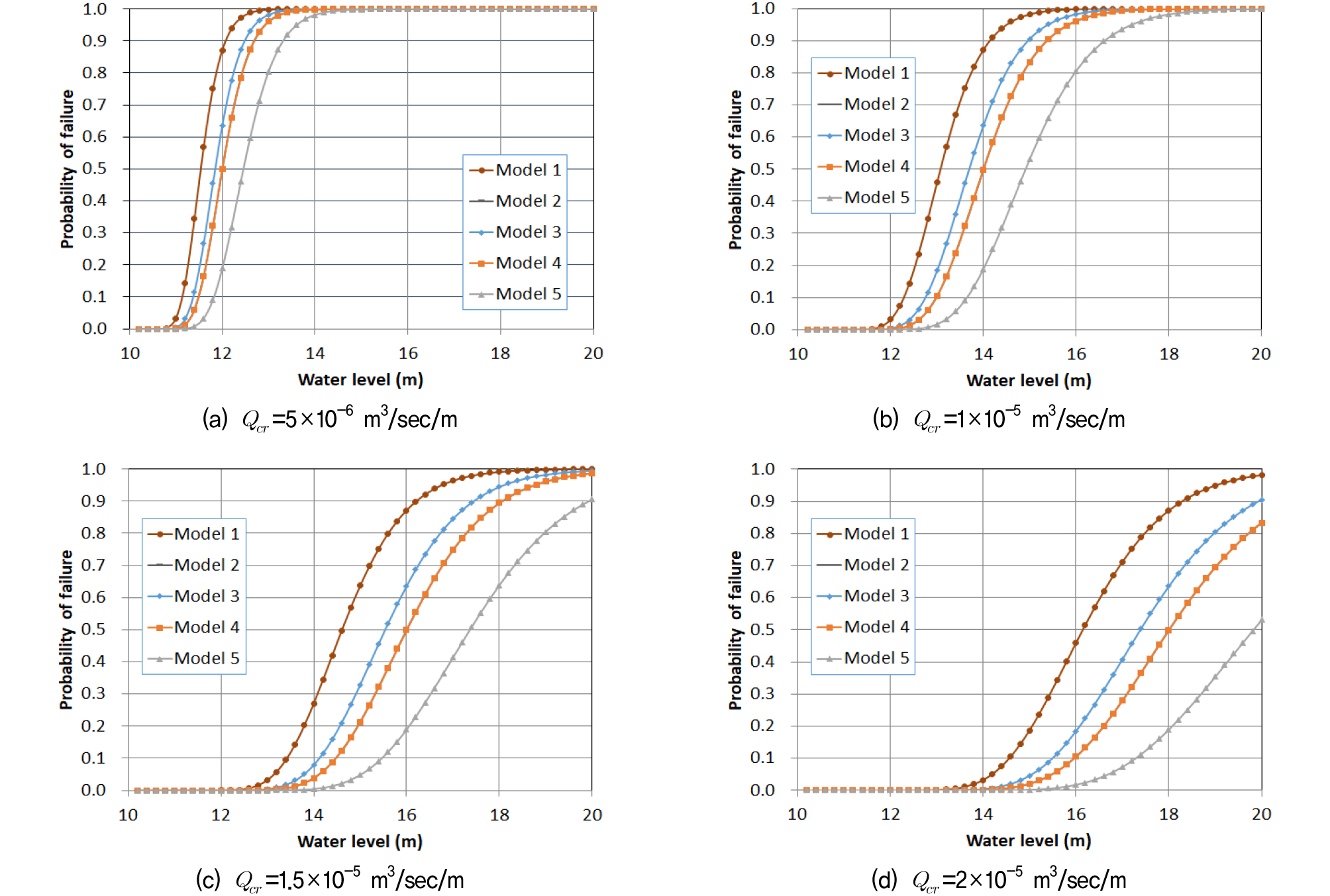
Fig. 11은 한계상태를 계산하는 데 사용된 한계 침투율에 따른 취약도 곡선을 구한 것이다. 한계침투율이 5×10-6m3/sec/m인 경우에는 모든 해석모델에서 곡선의 기울기가 급하여 단 몇 미터의 수위 증가에 침투량이 한계침투율을 초과하여 파괴상태에 도달하였다(Fig. 11(a)). 한계침투율이 커질수록 모든 해석모델에서 곡선의 기울기가 완만해졌다. 침투량의 경우에는 차수벽이 상·하류에 모두 설치된 경우의 거동이 제일 우수하고 차수벽이 설치되지 않은 경우가 제일 불량하였다. 상류부 설치(Model 2)와 하류부 설치(Model 4)의 경우에는 침투량에 대한 취약도 곡선이 완전 같게 계산되었다.
취약도 곡선을 사용하면 수위의 증가에 따른 위험도의 변화를 정량적으로 평가할 수 있다. 안정성 평가를 위해 결정론적 해석으로부터 수위에 따른 파괴모드별 안전율 변화를 구하여 활용할 수도 있지만, 안전율은 불확실성을 고려할 수 없으므로 안전에 대한 정량적인 정보를 제공하지 못한다. 예를 들어 수위 감소에 따라 안전율이 2배가 되었다고 2배로 안전하다고 말할 수 없다. 이에 비해 파괴확률은 파괴에 대한 정량적 정보를 제공하므로 구조물의 신뢰도, 취약도를 평가하기 위해 효과적으로 적용될 수 있다.
6. 결 론
기후변화로 인하여 홍수 발생강도, 빈도, 피해규모 등이 지속해서 증가하고 있어 극한 홍수에 대한 수리구조물의 침투파괴 위험도를 평가하고 관리하는 것이 점점 중요해지고 있다. 더불어 댐, 제방 등 홍수방어를 위한 기반시설의 효과적인 자산운용을 위해서는 예상되는 하중에 대한 구조물의 성능을 평가할 필요가 있으며 이를 위해 취약도 곡선이 활용되고 있다. 본 연구에서는 확률론적 해석을 바탕으로 취약도 곡선을 결정하는 방법을 연구하고 침투조절 공법에 따른 수리구조물의 취약도 곡선을 연구하였다.
투수계수가 확률론적으로 평균과 표준편차로 정의되는 대수정규분포를 따를 때 투수계수의 공간적 변동성을 고려한 수리구조물의 기초지반에서의 침투거동에 대한 MCS 결과로부터 얻어진 유출동수경사, 양압력의 합력, 단위 시간당 침투수량의 확률분포는 대수정규분포로 나타낼 수 있었다. MCS로부터 평가된 지반의 침투거동에 대한 확률분포로부터 파괴모드별로 수위 변동에 따른 파괴확률을 구함으로써 효율적으로 취약도 곡선을 작성할 수 있었다.
파괴확률은 파괴에 대한 정량적 정보를 제공하므로 취약도 곡선을 사용하면 다양한 파괴모드에 대하여 수위의 증가에 따른 위험도의 변화를 정량적으로 평가할 수 있다. 따라서 적용 가능한 침투조절 공법에 따른 취약도 곡선을 작성하면 구조물의 신뢰도, 취약도를 효과적으로 평가할 수 있어 안전성 및 경제적 측면에서 최대의 편익을 얻을 수 있는 침투조절법을 효과적으로 결정할 수 있을 것으로 판단된다.