1. 서 론

한반도는 판 내부에 위치하여 지각 활동이 활발하지 않고 국내에서는 최근 수십년간 규모 5 이상 중대규모 지진의 발생이 뜸하였다. 그러나 최근 들어서는 국내에서도 2016년 9.12 지진, 2017년 포항 지진과 같은 과거 대비 이례적으로 큰 규모의 지진들이 발생한 바가 있다. 9.12 지진의 경우 한반도 지진 관측 이래 최대규모인 국지 규모(M_L) 5.8에 달했으며 진앙으로부터 약 8km 떨어진 울산(USN) 관측소에서는 0.4g에 달하는 최대지반가속도(Peak Ground Acceleration, PGA)가 관측되었다(Kang et al., 2016). 9.12 지진 및 포항 지진 당시 내진 성능이 충분하지 않은 건물이나 비구조 요소에 대한 피해가 상당했으며 결과적으로 9.12 지진 당시 110억 원, 그리고 포항 지진 당시 850억원에 달하는 규모의 재산 피해가 발생하였다(Ministry of the Interior and Safety, 2017). 이러한 사례들을 계기로 한반도 내 지진 재난 발생 가능성에 대한 인식 및 관련 정부 정책 등에 큰 변화가 일어나고 있으며, 국내 특성을 반영한 지진재해 연구의 중요성 또한 재평가되고있다.

지진 피해의 공간적 분포는 지층의 형상 및 지반의 동적 거동 특성과 같은 지반 조건에 따라 달라지는 부지 증폭 현상(Site amplification effects)과 밀접한 관련이 있다는 것이 과거의 많은 지진 사례를 통하여 알려진 바 있다(Seed et al., 1991; Takemiya and Adam, 1997; Tezcan et al., 2002). 8.0에 달하는 모멘트 규모(M_w)를 가지는 1985년 멕시코시티 대지진은 부지 증폭 현상의 대표적 사례로 들 수 있으며, 당시 증폭 현상이 의심되는 지반운동이 연약지반에 위치한 다수의 관측소에서 기록되었다. 지진파의 증폭 현상은 지반 고유진동수(Natural vibration frequency, f₀)에 해당하는 진동수에서 집중적으로 발생하는 경향이 있으며, 멕시코시티 지진 당시 호성 퇴적층 지반에 위치한 관측소들에서 주변 암반 관측소 대비 수십배에 달하는 지반운동 푸리에 스펙트럼(Fourier spectrum)이 기록되었다(Singh, 1988).

본 연구의 대상 지역인 김해평야는 한반도 남동부 낙동강 하구 삼각주와 그 인근의 평야 지대를 포함하며, 행정구역 상으로는 부산시 강서구 일부 및 김해시 일부에 걸쳐 분포하고 있다. 최근 부산 균형 발전 및 인구 집중 현상의 해결책으로 명지국제신도시, 에코델타시티 등 여러 개발사업이 진행되고 있으며 이로 인해 본 연구 대상지역에 상당한 인구 유입이 발생하고 있다. 김해평야 지역 인근에는 활성단층으로 알려진 양산단층, 울산단층을 포함한 여러 단층대가 분포하며, 김해평야 북부를 관통하는 양산 단층은 Lee et al.(1999)에 의해 4기 역층 퇴적 이후에도 활동했음이 밝혀졌다. 또한, 한반도 동남권 지역은 국내 타 지역 대비 상대적으로 높은 지진 재해도를 가진 것으로 평가되고 있다(Park et al., 2021). 김해평야가 위치한 낙동강 삼각주는 연약점토층 및 조립토층으로 구성된 신생대 4기 퇴적층이 80m 내외의 두께로 넓고 깊게 분포하며, 지표부터 하부 약15m내외 까지 사질토로 형성되어 있고 그 아래에 연약점토층이 두껍게 퇴적되어 있는 형상을 보인다(Kim et al., 2014). 이로 인해 인근 지역에서 강진 발생시 김해평야 퇴적층 내에서 부지 증폭 현상에 의해 지진파가 상당히 증폭될 것으로 예상되며, 해당 지역에 대한 신뢰성이 높은 지진 재해도 분석 또는 피해 규모 예측을 위해서는 퇴적층 지반 전역을 대상으로 지반운동 증폭 특성의 정량화가 필요할 것으로 판단된다.

부지 증폭 현상을 설계 지반운동에 반영하기 위해서는 암반 지반운동을 입력값으로 하여 지반응답해석(Site response analysis)의 결과로 나온 지표면의 지반운동을 적용하는 방법을 적용할 수 있으며(Kramer, 1996), 간략화된 방법으로는 설계기준에 근거한 지반 분류법을 적용하여 설계응답스펙트럼을 결정하거나, 경험적 증폭함수를 적용하는 방법도 적용된다(Campbell and Bozorgnia, 1994). 어떤 방법을 적용하더라도, 지반증폭효과를 지반운동에 반영하기 위해서는 대상 지반의 동적 거동 특성을 정량화할 필요가 있다. 지반응답해석의 수행을 위해서는 기반암까지의 전단파 속도, 밀도 등이 필요하고 지반 분류에 의한 설계 스펙트럼이나 경험적 증폭함수의 적용에는 지표면 아래 30m의 평균 전단파 속도(V_s30)나 지반 고유주기(T₀) 등이 필요하다.

본 연구는 지반응답해석, 지진재해도분석 등에 활용하기 위해 김해평야 퇴적층 지반의 전단파 속도 모델을 개발하는 것을 목표로 한다. 이를 위해 총 6개소의 실험 위치를 대상으로 이동식 속도지진계를 이용한 상시미동 수평-수직비(Horizontal-to-Vertical Spectral Ratio, HVSR) 방법을 적용하여 지반 고유진동수를 측정하고, 상시미동 표면파 분석법(Microtremor Array Method, MAM)으로 기반암 깊이 까지의 전단파 속도 주상도를 도출하였다. 또한, 현재까지의 실험 결과에 근거하여 퇴적층의 전단파 속도 모델을 깊이의 함수로 도출하였다.

2. 실험 방법 및 실험 위치

2.1 상시미동 수평-수직비

퇴적층 지반의 지표면 운동과 기반암 운동의 푸리에 스펙트럼 비를 전달함수(Transfer function)라 하며, 전달함수는 기반암층에 단위 임펄스가 작용할 때의 지표면 응답을 진동수 영역에서 표현한다. 또한, 퇴적층 지표 운동과 인근 암반에 위치한 기준관측소에서 계측한 기반암 운동의 스펙트럼비를 표준스펙트럼비(Standard Spectral Ratio, SSR)라 한다(Borcherdt, 1970). 단위 임펄스 작용시 지표면 응답(자유진동)의 우세진동수를 지반의 고유진동수라 하며, 지진 발생시 지반의 고유진동수에 해당하는 영역에서 지반운동의 증폭이 주로 발생한다. 기반암 상부에 균질한 단일층으로 이루어진 지반의 경우 지표면 운동의 고유 진동수(f₀)는 식 (1)과 같이 토층 전단파 속도(V_S)와 기반암 상부 두께(H)의 관계식으로 표현될 수 있다(Kramer, 1996).

또한, 퇴적층과 기반암층의 전단파 속도 차이가 큰 경우 지반운동의 증폭이 커지게 되며, 증폭의 정도는 아래 식 (2)로 정의되는 복소 임피던스 비와 관계가 있다.

여기서 ρ_s와 ρ_r은 퇴적층과 기반암의 밀도, v_ss와 v_sr은 퇴적층과 기반암의 전단파 속도, ζ_s와 ζ_r은 퇴적층과 기반암의 감쇠비를 의미한다. 일반적으로 퇴적층은 층상구조를 이루며 깊이에 따라 전단파 속도 및 밀도가 상이하고, 이러한 경우 지반운동의 전달함수는 단일층의 경우보다는 더 복잡한 형태를 보이나, 암반층까지의 밀도 및 전단파 속도 주상도가 존재하는 경우 1차원 지반응답해석을 통한 전달함수 및 지반 고유진동수의 결정이 가능하다.

그러나 실무에서는 전단파 속도 자료가 준비되어 있지 않은 경우가 많은데, Nakamura(1989)는 이러한 경우 HVSR을 활용하여 해당 지반의 지진파 증폭 특성을 추정할 수 있음을 제안하였다. 기반암 상시미동의 푸리에 스펙트럼을 수평(H_B), 수직 성분(V_B)으로, 지표면 상시미동의 푸리에 스펙트럼을 수평(H_s), 수직 성분(V_s)으로 표현하면 증폭비(As)은 식 (3)과 같이 표현 될 수 있다. 여기서 Nakamura(1989)는 기반암 상시미동 스펙트럼의 수평-수직비는 1에 근접함에 착안하여 식 (4)로 표현되는 상시미동 수평-수직비가 지반운동의 전달함수를 근사할수 있음을 제안하였다.

지반증폭효과의 실험적 평가를 위한 상시미동 HVSR 방법은 1990년대 이후 급격히 확산되어 왔다. 여러 후속 연구에서 상시미동 HVSR 방법으로 지반 고유 진동수를 효과적으로 측정할수 있음을 보였으나, 상시미동 HVSR로 지반운동의 전달함수를 효과적으로 추정할수 있는지 여부에 대해서는 연구자들의 논란이 이어지고 있다(Lermo and Chavez-Garcia, 1993; Rong et al., 2017; Stanko et al., 2019; Xu and Wang, 2021).

2.2 상시미동 기반 표면파 분석

레일리파(Rayleigh wave)나 러브파(Love wave)와 같은 표면파는 지표면을 따라 전달되므로 파장이 긴 경우 전단파 속도가 상대적으로 높은 지반의 심부를 통해 전달되며 파장이 짧은 경우 전단파 속도가 상대적으로 낮은 얕은 층을 통해 전달된다. 이러한 전달 특성을 표면파의 분산(dispersion) 특성이라 하며, 현장에서 표면파의 계측을 통해 획득한 분산곡선을 대상으로 역해석을 실시하여 지진파의 전달 속도를 깊이의 함수로 결정하는 과정을 표면파 탐사법이라 한다. 표면파 탐사법은 크게 능동 탐사 기법과 수동 탐사 기법으로 분류할수 있는데, 능동 탐사 기법에는 SASW(Spectral Analysis of Surface Waves) 방법(Nazarian and Stokoe, 1986)과 MASW(Multichannel Analysis of Surface Waves) 방법(Park et al., 1999)이 주로 쓰이고 있으며, 상시미동(Microtremor 또는 Ambient vibration) 기반의 수동 탐사 기법은 파의 진행 방향을 알 수 없는 표면파의 전파 특성과 관련하여 2차원 배열 기반의 Microtremor Array Method(MAM) 방법(Foti et al., 2018)이 주로 쓰인다.

상시미동 기반 표면파 분석법은 능동 탐사 기법에 비해 적은 수의 지진계 설치를 필요로 하고 인공적인 가진이 필요없어 적용성이 좋으며 낮은 주파수 대역의 상시미동을 측정하여 능동 탐사 기법에 비해 비교적 더 깊은 심도의 심부 지질 특성 추정이 가능하다(Yoon, 2007). 상시미동 기반 표면파 분석 기법은 (1) 배열을 통한 상시미동 계측, (2) 표면파 분선곡선 도출, (3) 분산곡선 역산을 통한 전단파 속도구조 추정의 세 단계로 구분된다. 표면파 분산곡선 도출 기법에는 HFK(High resolution f-k) 방법(Capon, 1969)과 SPAC(Spatial autocorrelation) 방법(Aki, 1957)이 흔히 적용되며 기존의 SPAC 방법을 수정 및 확장한 MSPAC(Modified spatial autocorrelation) 방법(Bettig et al., 2001) 또한 널리 사용되고 있다. 수동 표면파 탐사 기법에 사용되는 수신기의 배열은 Zywicki(1999)에 의해 중심에 대해 일정한 거리를 둔 원형 배열이 추천되었으며 그 이유는 (1) 각 수신기가 일정한 해상도를 갖고 있으므로 모든 방향의 해석에 제약이 없음, (2) 배열의 대칭성으로 인한 에너지 누수의 영향이 작음, (3) 해상도 특성이 우수함으로 나열할수 있다. HFK방법과 SPAC방법은 레일리파 분산곡선 도출 과정 및 특징에 차이가 있다. HFK 방법은 센서 배열을 통해 계측된 상시미동으로부터 주파수영역 빔포밍(frequency domain beamforming) 기법을 적용하여 주파수(f)-파수(k) 스펙트럼을 결정하고, 주파수-파수 스펙트럼에서 표면파 고유모드에 해당하는 극대점들을 추출하여 아래의 식 (5)와 같은 관계식을 이용하여 표면파의 위상속도를 주파수의 함수로 결정한다(Foti et al., 2018).

이와 달리 SPAC방법은 계측된 신호의 자기상관(autocorrelation)을 이용한 일관성을 통해 분산곡선을 도출하게 된다. 각각의 지진계를 통해 수신한 신호를 푸리에 변환하여 각 주파수에 대한 스펙트럼을 획득하게 되고 이에 대한 일관성 분석을 통해 분산곡선을 도출하는 과정으로 진행된다. SPAC방법은 HFK방법에 비해 적은 수의 지진계를 필요로 하고 배열의 기하학적 특성에 해상도가 의존하지 않으며 Bettig et al.(2001)이 제안한 MSPAC방법은 어느 정도 불규칙한 배열에도 적용이 가능하다.

또한 HFK방법과 SPAC방법은 서로 다른 장단점을 갖고 있다. 지배적인 송신원의 위치를 알고 있는 경우 HFK방법은 적용성이 좋으나 방위각에 대한 샘플링이 충분하지 않은 경우 SPAC방법에서는 송신원의 위치에 대한 인식은 편향된 추정 과정이 진행될 수 있어 불리하다. 또한 다양한 송신원은 HFK방법을 사용하는 경우 해상도의 저하를 야기할 수 있으며 HFK방법 및 SPAC방법 모두 센서 배열 사이 저주파 영역 자료에 대한 한계를 갖고 있다. 또한 HFK방법은 고유모드(fundamental mode)와 고차모드(higher mode)를 모두 감지 가능하나 SPAC기반 방법은 두 가지 모드가 함께 존재하는 경우 불리할 수 있다. 그리고 일반적인 경우 SPAC방법이 HFK방법에 비해 긴 파장 영역의 자료 추출이 가능하다. Foti et al.(2018)는 이러한 각각의 분산 곡선 도출 방법 및 특징, 그리고 장단점에 의해 두가지 방법을 모두 사용하여 비교하는 것이 분산곡선 도출 과정의 정확도를 높이는 방법으로써 추천하였다.

MAM방법을 적용하여 표면파 분산곡선 도출시 가탐심도는 센서 배열로 샘플링이 가능한 신호의 최대 파장(λ_max)에 의해서 결정되고, 최대 파장은 일반적으로 지진계의 최대 간격과 관계가 있다. 이론적 가탐심도는 적용되는 신호처리 방식에 따라 달라질수 있으나, HFK방법의 경우 일반적으로 양호한 조건의 경우 가탐심도가 센서 최대 간격에 근접하며, SPAC 방법의 경우 일반적으로 HFK방법에 비해 2~5배 가량 더 큰 가탐심도를 가지는 것으로 알려져 있다(Foti et al., 2018).

2.3 실험 방법

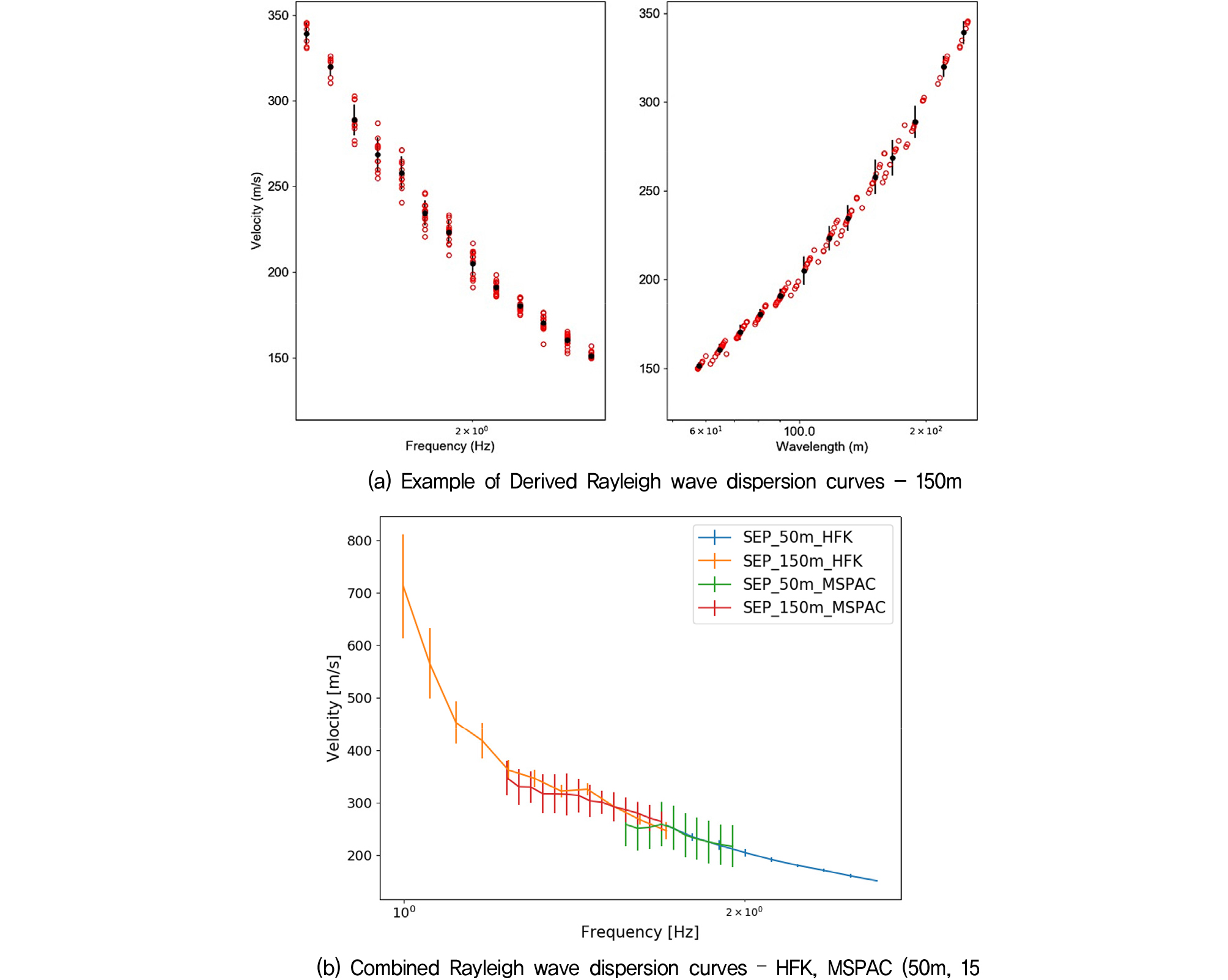
본 연구에서는 Fig. 1(a)에 보여진 이동식 속도 지진계(Trillium Compact 20s) 6기를 활용하여 각 실험 위치에서 지표면 상시미동 자료를 획득하였다. 센서 배열을 이용하여 표면파 분산곡선을 도출할 경우 측정 가능한 파장의 범위는 센서간 최소간격 및 최대간격에 의해 결정된다. 일반적으로 파장이 짧은 표면파를 계측하기 위해서는 센서간 최소 간격이 좁을 필요가 있고 긴 파장의 표면파를 계측하기 위해서는 센서간 최대간격이 클 필요가 있으므로, 최대한 넓은 대역폭에서 상시미동 표면파를 계측하고 활용하기 위해 Fig. 1(b)와 같이 다양한 직경(예, 5m, 15m, 50m, 150m, 400m)을 가지는 원형으로써 최대 5개의 센서 배열을 적용하였다. 각 배열 당 최대 1시간까지 상시미동을 측정하였다.

Fig. 1

Seismic sensor (Trillium Compact 20s) and example of seismic sensor array

3방향의 진동요소를 정확히 측정하기 위해 나침반이 북쪽을 가리키는 자북 방향을 기준으로 설치하였으며 지진계의 수평계를 활용하여 수평을 확인하였고 알루미늄 평면 플레이트에 스파이크를 결합하여 최대 10cm 이상 밀어 넣어 지진계를 지표면에 고정하였다. 그리고 각 지진계의 정확한 설치 위치 파악을 위해 U-blox사의 GNSS 모듈을 탑재한 ZED-F9P Real Time Kinematic(RTK) Receiver를 활용하였고 국토지리정보원의 NTRIP 서비스를 이용하여 정밀측량을 진행하였다. 계측된 상시미동 자료는 Geopsy(https://www.geopsy.org) 프로그램을 활용하여 HVSR 및 표면파 분산곡선을 도출하였다. 계측된 상시미동에서 분산곡선을 도출하는 과정에서는 MSPAC방법과 HFK방법을 모두 적용하여 Fig. 2(a)와 같이 각 배열의 분산곡선을 도출하고 취합하여 Fig. 2(b)와 같이 고유모드 레일리파 분산곡선을 도출하였다.

Fig. 2

An example of derived Rayleigh wave dispersion curves (Samnack Eco Park)

분산곡선 도출 후 역해석 프로그램 Dinver를 통해 분산곡선 역해석 과정을 수행하였으며, 레일리파 분산곡선과 지반 고유진동수를 역해석 타겟으로 설정하였다. 역해석 과정에서 지반은 동일한 V_p, V_s, 밀도 및 포아송비를 가지는 6개의 균질한 지층으로 가정하였으며, 최하부 기반암층은 V_s=3,500m/s인 반무한층으로 가정하였다. Dinver에는 표면파 분산곡선의 역해석을 위해 직접탐색법(direct search algorithm)의 일종인 Neighbourhood algorithm(Wathelet, 2008)이 구현되어 있으며, V_p, V_s 등과 같은 매개변수들 사이의 물리적 조건들을 고려해 지반 모델의 무작위 샘플을 생성하고 모델의 이론적 분산곡선과 계측된 분산곡선의 Misfit을 최소화 하는 방식으로 역해석을 실시하게 된다. 또한, 역해석 결과로 얻은 전단파 속도 주상도와 비교하기 위해 국토교통부 국토지반정보 통합DB센터의 지반정보포털시스템을 활용하여 실험 진행 위치 인근 1km 내 위치에서 수행된 시추주상도 자료를 수집 및 분석하였다.

2.4 실험 위치

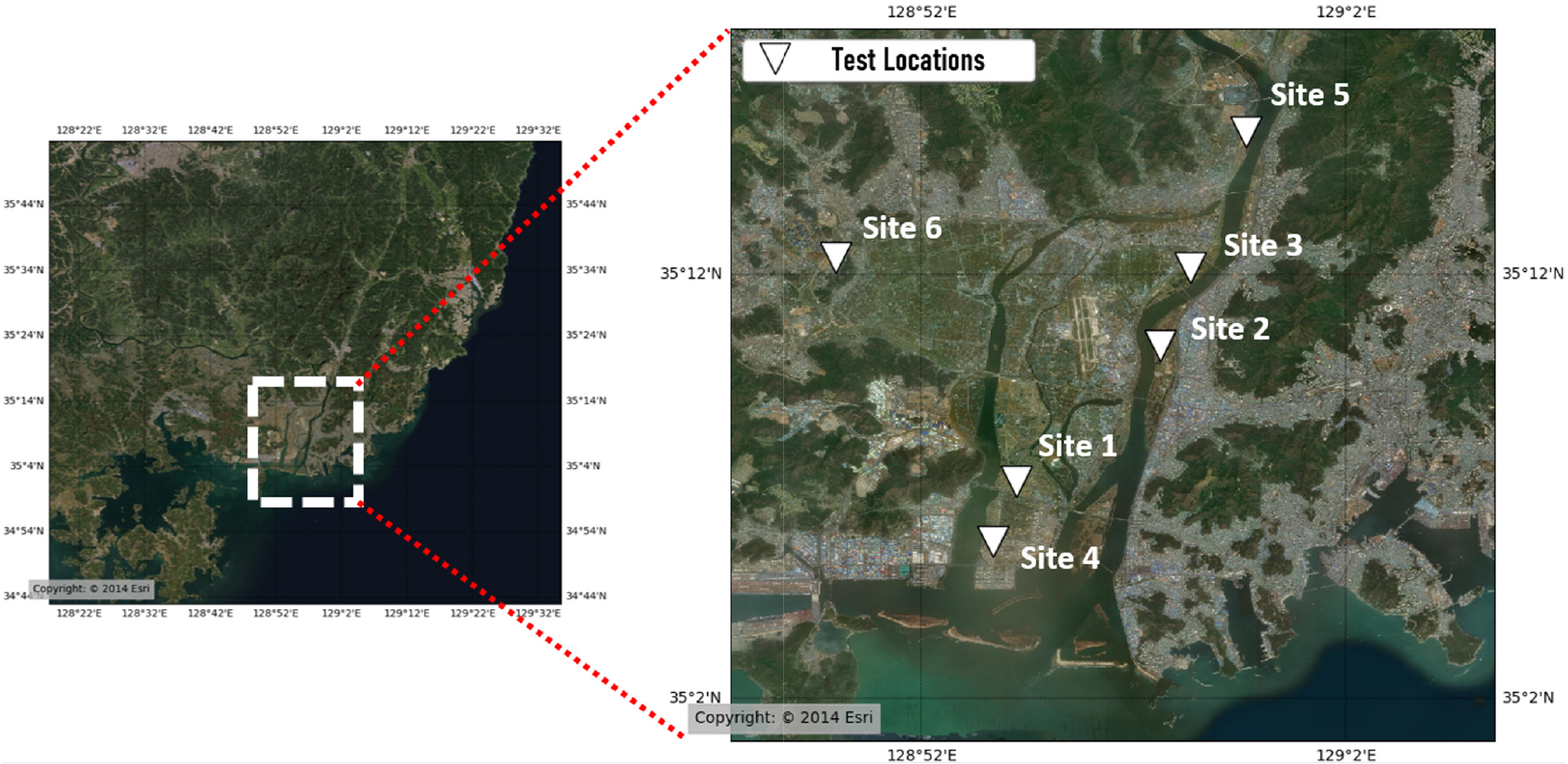
본 연구에서는 김해평야 지역의 상시미동 자료를 획득하고 분석하기 위해 실험의 특성을 고려하여 김해평야 인근에 Fig. 3과 같이 총 6개의 실험 위치를 선정하여 실험을 진행하였다. 실험 위치는 평지지형에서 직경 100m 이상의 배열이 설치 가능하고 접근성이 양호한 위치를 선정하였으며, 퇴적층 특성의 공간적 변화를 고려할 수 있도록 공간적으로 충분히 분산된 위치들을 선정하였다. 각 실험 위치에서 적용한 배열의 최대 직경은 Site 1의 경우 400m이며 이외의 위치에서는 모두 150m를 적용하였다.

Fig. 3

Map of test locations (Sites 1 ~ 6)

3. 결과 및 토의

3.1 상시미동 수평-수직비 분석 결과

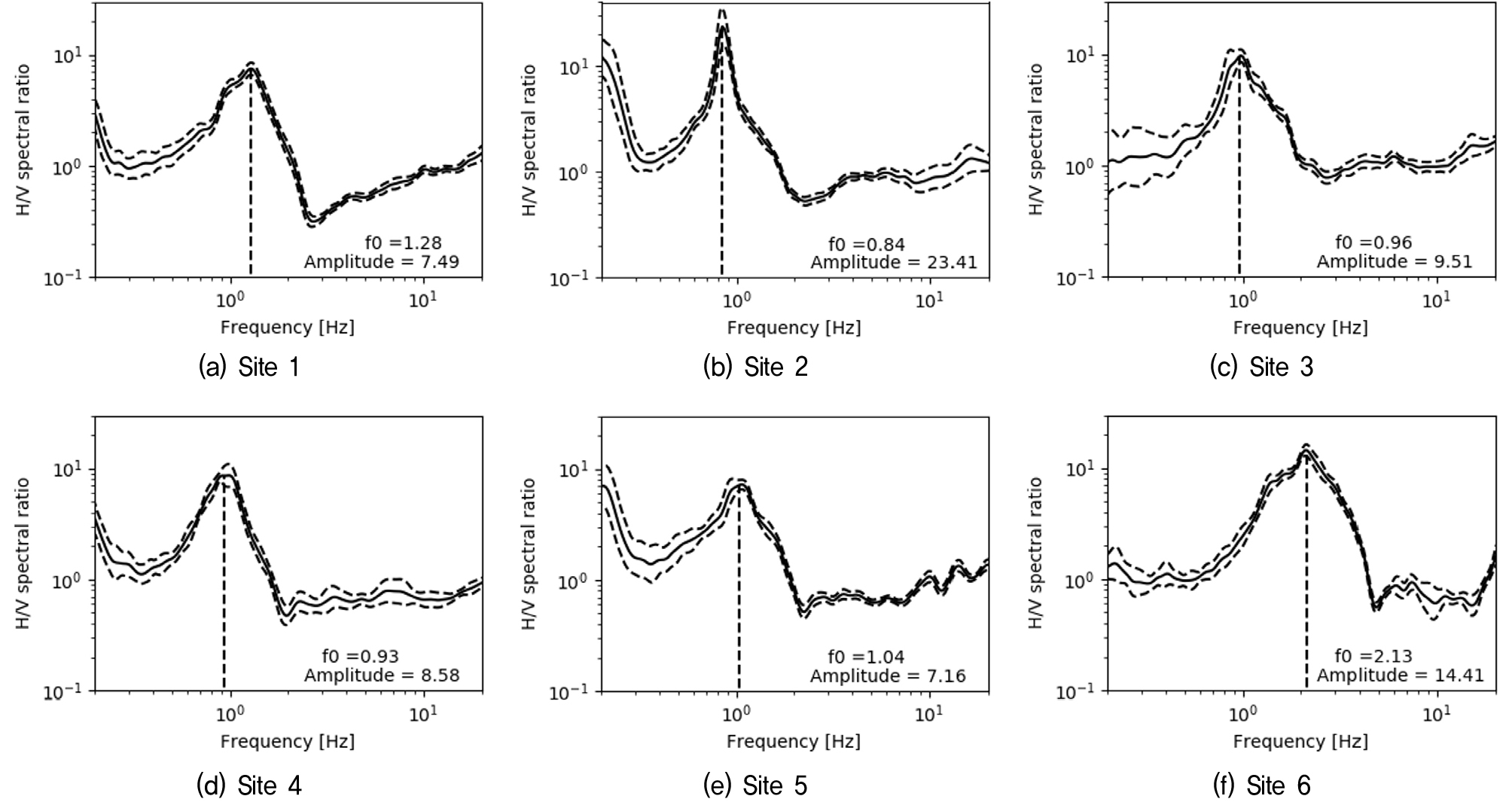
Fig. 4는 각 실험 위치에서의 HVSR 측정 결과를 보여준다. 6개소 모두에서 f₀이 뚜렷하게 파악되고 있으며 SESAME Guideline에서 제시된 ‘Clarity’ 기준을 만족하는 것으로 나타났다. Sites 1~5는 낙동강 본류 또는 서낙동강 인근 퇴적층에 위치하고 있으며, 고유진동수는 f₀=0.84~1.28Hz로 나타났다. Site 6는 낙동강 본류 및 서낙동강에서 멀리 떨어져 있고 상대적으로 지대가 높으며 김해시에 위치한 칠산이라 하는 야산(해발 고도 89.8m) 인근에 위치하고 있어 상대적으로 퇴적층이 얕을 것으로 예상되며, 고유진동수는 f₀=2.13H_z로 타 위치들에 비해 높게 나타났다.

Fig. 4

Result of microtremor HVSR (f₀ and f₀ amplitude)

f₀에서 HVSR의 증폭계수는 7~23으로 상당히 높게 나타났다. 선행연구에 따르면 HVSR 방법으로 결정한 f₀은 실제(지진시 기준관측소 대비 SSR방법으로 측정한) f₀와 유사한 경우가 대부분이다. 반면, HVSR 방법으로 결정한 지반운동 증폭 계수는 SSR 방법과 유사하거나 작은 경우가 대부분이며, 이에 따르면 HVSR상의 증폭계수는 실제 지반운동 증폭계수의 하한값에 근접한다 할 수 있다(SESAME guideline, 2004; Lermo and Chavez-Garcia). SESAME Guideline(2004)에 따르면 “clarity” 기준을 만족하고 f₀에서 HVSR의 값이 4~5를 초과하는 거의 모든 경우에 퇴적층과 하부 암반층 사이에 큰 임피던스 대조가 존재함을 의미한다. 본 연구에서 실험을 실시한 6개소 모두 위 조건을 만족하는 것으로 나타났다.

HVSR의 경우 f₀ 보다 높은 진동수 영역에서는 값이 상당히 작은 경우가 대부분이나, 동일한 위치에서 SSR을 측정하는 경우 f₀ 보다 높은 고진동수 영역에서도 증폭이 발생하는 경우가 많고, 이는 지진파의 증폭이 고유진동수보다 높은 진동수에서도 발생 할 수 있음을 의미한다(SESAME Guideline, 2004). 따라서, 김해평야 인근지역에서 중규모 이상의 강진이 발생할 경우 퇴적층의 거동에 의한 지반운동 증폭현상으로 f ≥ 1hz의 진동수 대역에서 지반운동의 증폭이 발생할 것으로 판단되며, 실제 전달함수의 증폭계수는 HVSR이 보여주는 값보다 더 큰 경우가 대부분이므로 증폭의 규모 또한 상당할 것으로 예상된다.

3.2 상시미동 기반 표면파 분석 결과

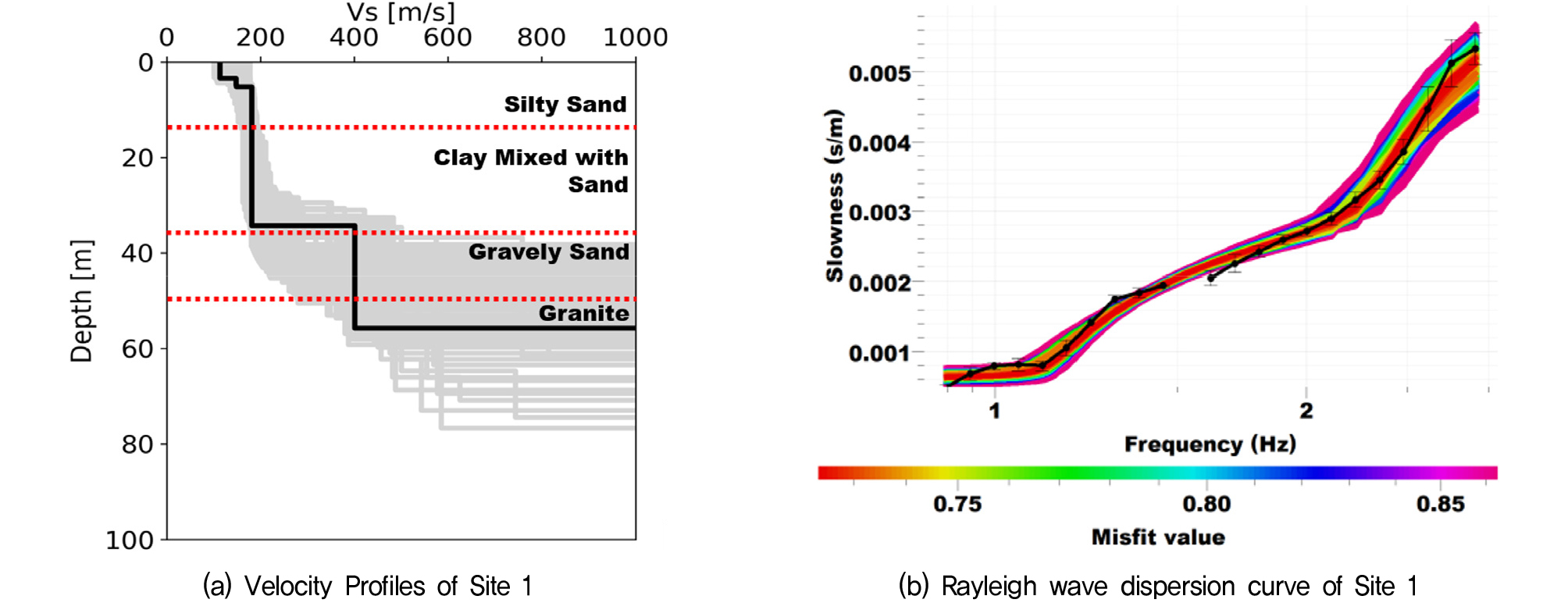
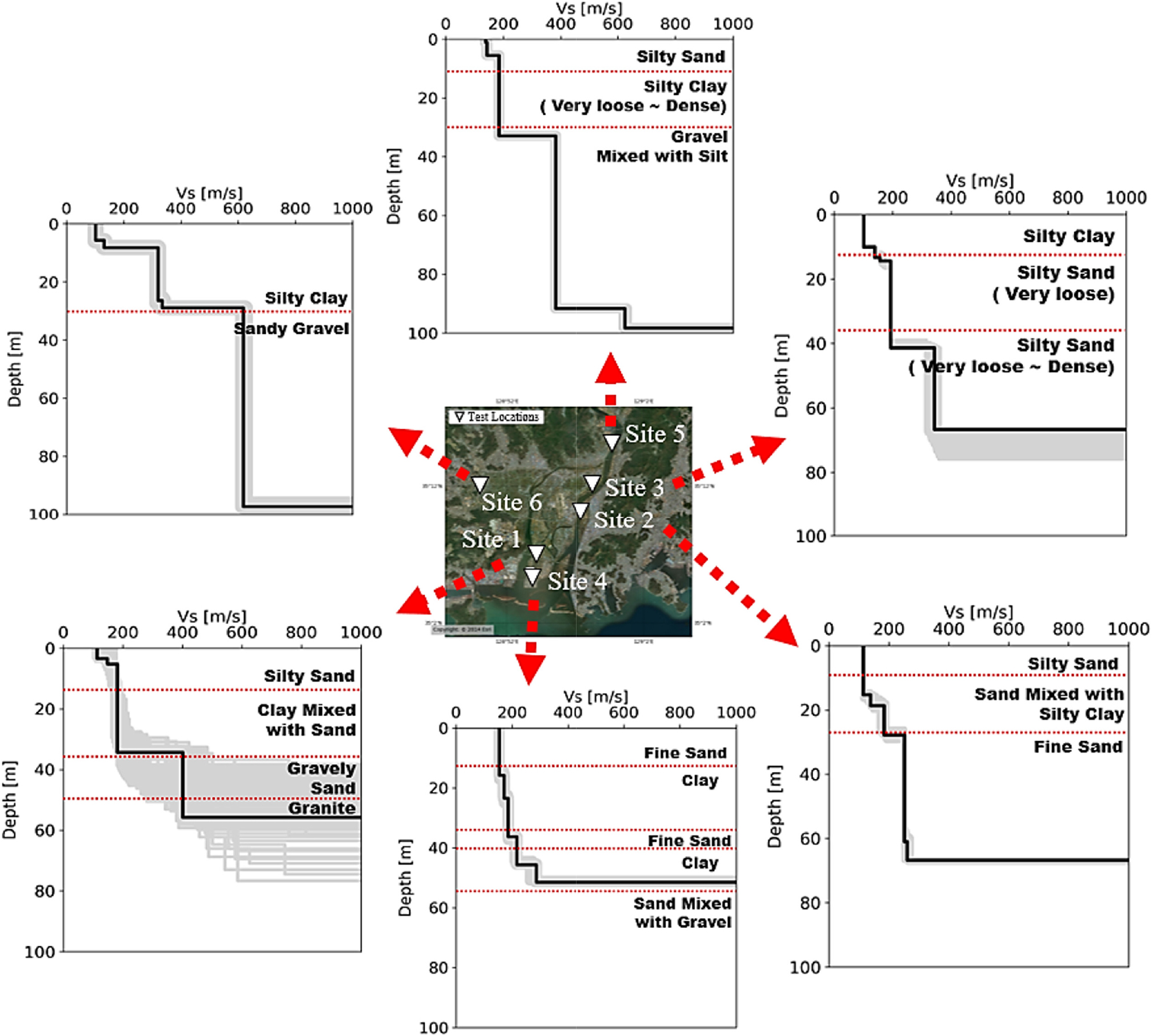
전단파 속도 주상도 도출 결과와 지반정보포털시스템을 통해 획득한 시추 주상도 자료의 시추 종료 심도까지의 심도별 토질 분류의 예시를 Fig. 5(a)와 같이 표시하였다. 이를 통해 속도 주상도 도출 결과에서 전단파 속도가 급격하게 변하는 구간에 대한 시추주상도 상의 토질 분류의 변화가 확인 가능하다. 또한 Fig. 5(b)는 실험에 의해 도출된 레일리파 분산곡선과 역해석에 사용된 속도 주상도의 이론적 분산곡선을 정량적으로 비교하여 이론적 분산곡선이 실험적 분산곡선과 얼마나 다른지의 정도를 Misfit 값으로 보여준다.

Fig. 5

(a) Comparison of derived velocity profiles and stratigraphy data at Site 1. (b) Comparison of experimental and theoretical Rayleigh wave dispersion curves at Site 1

모든 실험 위치에 대한 분산곡선 역산 결과에서 Misfit이 작은 순서대로 1,000가지 경우에 대한 전단파 속도 주상도 도출 결과를 Fig. 6과 같이 도시하고 Misfit이 가장 작은 경우의 속도 주상도를 굵은 선으로 표시하였다. Site 6을 제외한 모든 위치에서 V_s = 200m/s 내외의 퇴적층이 지표면 하부 30m 이상으로 깊이 발달해 있는 것을 알 수 있으며, Sites 1, 3, 5, 6에서 기반암층 바로 윗쪽에 V_s = 400m/s 전후를 나타내는 퇴적층이 분포하고 있는 것으로 나타났다. 또한 60m~100m 사이의 깊이에서 전단파 속도가 크게 증가함을 파악할 수 있고 이를 통해 해당 깊이에서 기반암이 존재함을 추정할 수 있다.

Fig. 6

Result of derived shear wave velocity profiles in the test locations

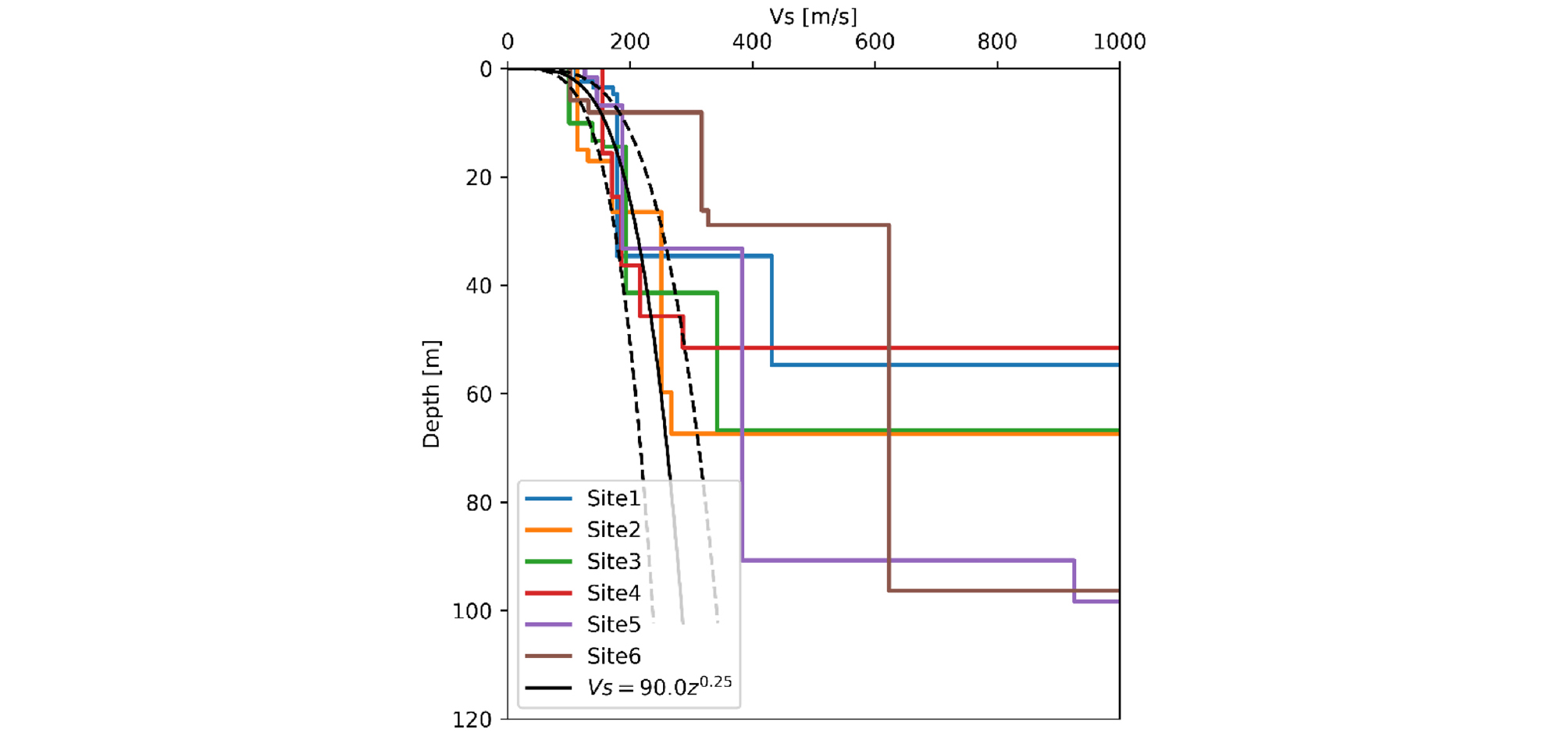
Fig. 7은 Site 6을 제외한 5개 실험 위치의 속도 주상도를 통해 도출한 김해평야 지역 퇴적층의 대표 전단파 속도 주상도 모델을 보여준다. 해당 모델은 식 (6)으로 표현되며 이를 활용하여 김해평야 내 천부 퇴적층 지반의 깊이에 따른 전단파 속도 변화를 추정 가능하다. 또한 그림에서 점선은 식 (6)의 계수를 20% 내외로 변화시켰을 때의 범위를 보여준다.

Fig. 7

Representative shear velocity model of Gimhae Plains. Bounds shown as dashed lines are obtained by varying the coefficient of equation (6) by 20%

Site 6는 인근에 야산이 위치해 있으며 시추주상도 분석 결과 기반암층의 지형에 경사가 있고 얕은 깊이에서 풍화암이 발견되었다. Fig. 6에서 Site 6는 8m이상의 깊이에서 다른 위치들에 비해 전단파 속도가 상당히 크게 나타나고 있는데 이는 풍화암층이 얕은 깊이에서 나타나는 Site 6의 지질 특성과 연관되어 있는 것으로 보인다. 그러나 그 외 5개의 시험위치에서는 지표면 하부 천부 퇴적층의 깊이에 따른 속도증가가 서로 유사하게 나타나고 있으며, 불확실성이 존재하기는 하지만 Site 6를 제외한 5개의 시험 위치의 천부 퇴적층 전단파 속도는 전반적으로 식 (6)의 전단파 속도-깊이 모델에 의해 대표될 수 있을 것으로 판단된다.

3.3 낙동강 퇴적층 지질 특성과의 관계

신생대 4기 플라이스토세 후기 무렵에는 해수위가 현재보다 상당히 낮아 낙동강 인근 평야지역은 백악기 기반암 위에 자갈층과 모래층이 우세한 하성 퇴적층이 형성되어 있는 것으로 알려져 있다(Ham et al., 2018; Yoo et al., 2020). 이후 해침이 시작되며 하성 퇴적층 위에 실트질 및 점토질 흙이 우세한 후기 플라이스토세 천해 퇴적층과 초중기 홀로세 천해 퇴적층이 형성되었고, 그 후 해수면이 상승이 더뎌지다가 서서히 후퇴하는 과정에서 후기 홀로세 모래질 삼각주 퇴적층이 형성된 것으로 알려져 있다.

따라서, 낙동강 인근 평야지대 전역에서 4기 퇴적층의 구성은 플라이스토세 후기에 형성된 자갈질 또는 모래질 하성퇴적층, 플라이스토세 후기에서 홀로세 초중기에 형성된 실트질 또는 점토질 해성 퇴적층, 그리고 후기 홀로세 모래질 삼각주 퇴적층으로 구성되어 있을 것으로 예상된다. 본 연구 대상 위치 인근의 시추 주상도를 검토한 결과 전반적으로 위와 같은 퇴적특성이 보이고 있으며, 유사한 시기에 퇴적된 지층은 전단파 속도도 크게 다르지 않을 것으로 기대되므로 Fig. 6과 같이 서로 유사한 속도 주상도가 나타나는 것으로 보인다. 다만 몇몇 시험위치에서는 기반암층 바로 윗층에서 전단파 속도가 300~400m/s으로 지표층보다 상당히 높은 층이 존재하며, 해당 깊이에서는 전단파 속도가 식 (6)에 의해 예측되는 값보다 상당히 높게 나타나고 있음을 알 수 있다. 이는 플라이스토세 후기에 형성된 자갈질 모래층(심부 퇴적층)의 전단파 속도가 이후에 퇴적된 해성 퇴적층보다 더 크기 때문일 것으로 판단되며, 따라서 식 (6)이 나타내는 전단파 속도 모델은 플라이스토세 후기 해침 이후에 형성된 퇴적층에만 적용이 가능할 것으로 판단된다.

3.4 국내 내진설계 실무 관련 고려사항

국내 시설물 내진설계 기준인 내진설계 일반(KDS 17 10 00)은 국지적인 토질조건, 지질조건과 지표 및 지하 지형이 지반운동에 미치는 영향을 고려하기 위해 설계지반운동 결정시 지반을 S1에서 S6까지 6종으로 분류하여 지반 분류 등급에 따라 설계지반운동을 달리 하도록 한다. 이 중 S6 지반은 부지 고유의 특성평가 및 지반응답해석이 필요한 지반으로, 퇴적층 하부 기반암 깊이가 50m를 초과하는 경우도 S6지반으로 분류되게 된다. HVSR에서 지반 고유진동수가 명확히 결정되고 퇴적층과 하부 기반암층 사이의 임피던스 대조가 상당할 것으로 판단되는 경우, 퇴적층의 평균 전단파 속도가 알려져 있다면 h = V_s / 4f₀ 관계식을 적용하여 기반암의 깊이를 추정할 수 있다. 본 연구 대상지역 퇴적층의 평균 전단파 속도가 V_s = 200m/s 내외라고 가정하면 고유진동수가 f₀ < 1Hz인 경우 기반암 깊이가 50m를 초과함을 의미하므로 S6지반으로 분류되어 지반응답해석을 필수적으로 수행해야 한다. 본 연구의 경우 총 6개소중 3개소에서 f₀ < 1Hz의 고유진동수가 관측되었고, 나머지 3개소 중 2개소도 f₀ = 1Hz에 근접하는 고유진동수가 관측되었다. 퇴적 특성이 유사한 김해평야 지역 내 타 위치들에서도 고유진동수가 유사하다고 하면 기반암 깊이까지의 평균 전단파 속도에 따라 평야지대 내에서 S6지반으로 분류되는 면적은 상당할 것으로 예상된다. 또한 식 (6)과 계측된 f₀을 이용하여 기반암 깊이를 추정할 경우 퇴적층 최하부에 자갈질-모래질 하성 퇴적층이 두텁게 존재한다면 기반암 깊이가 저평가될 수도 있을 것으로 생각되며, 따라서 식 (4)와 계측된 f₀을 적용하여 S6 지반으로 분류되는 경우는 실제 S6지반에 해당할 확률이 매우 높을 것으로 판단된다.

4. 결 론

김해평야 퇴적층의 전단파 속도 구조를 파악하기 위해 상시미동 수평-수직비 분석 및 상시미동 기반 표면파 분석을 실시하였다. HFK방법(Capon, 1969) 및 MSPAC방법(Bettig et al., 2001)을 사용하여 레일리파 분산곡선을 도출하였으며 도출된 분산곡선을 Neighborhood algorithm(Wathelet, 2008)을 적용하여 역해석을 통해 김해평야 내 실험 위치의 속도 주상도를 획득하였다. 본 연구의 결과를 바탕으로 다음과 같은 결론을 도출하였다.

(1) 김해평야 지역의 퇴적층 지반은 대체로 1Hz 내외의 고유진동수를 가지며, HVSR은 f₀에서 상당히 큰 증폭계수를 보여준다. 따라서, 인근 지역에서 지진 발생시 1Hz 이상의 진동수 대역에서 지반운동이 크게 증폭될 것으로 예상된다.

(2) 상시미동 기반 표면파 분석 결과 김해평야 내 천부 실트질 및 점토질 퇴적층은 대체로 V_s = 200m/s 내외의 전단파 속도를 보이며, 천부 퇴적층과 기반암층 사이에 V_s = 400m/s 전후의 심부 퇴적층이 존재하는 경우가 확인되었다. 또한 대체로 60m~100m 사이에서 기반암이 분포하는 것으로 추정되었다.

(3) 전체 6개 위치의 해석 결과를 통해 김해평야 지역에서 후기 플라이스토세 해침이 시작된 이후 형성된 천부 퇴적층의 전단파 속도 주상도 대표 모델을 도출하였으며 다음과 같이 표현 가능하다.

(4) 본 연구 실험 대상 위치 6개소 중 3개소에서의 상시미동 수평-수직비 결과 f₀ < 1Hz의 지반 고유주파수가 관측되었다. 평균 전단파 속도가 V_s = 200m/s 내외라고 가정하면 김해평야 내 내진설계 일반(KDS 17 10 00)에서 부지 고유의 특성평가 및 지반응답해석이 필요한 S6 지반에 해당하는 면적이 상당할 것으로 예상된다.