1. 서 론
2. 동적원심모형실험 수행
3. 응답스펙트럼해석 수행
4. 경사말뚝이 적용된 잔교식 구조물의 동적 거동 분석
5. 경사말뚝이 적용된 잔교식 구조물의 응답스펙트럼 해석
6. 결 론
1. 서 론
잔교식 구조물은 상판을 말뚝 또는 기둥으로 지지하는 형식의 항만 구조물로서 작게는 수 m, 크게는 수 km 규모에 달하므로 실물 크기 구조물의 지진 실험을 수행하는데 어려움이 있다. 그러므로 3차원 수치 모델링 기법을 이용하여 구조물의 내진성능을 평가할 수 있다. 국제해운협회(PIANC, 2001), 미국 토목학회(ASCE, 2014), 그리고 대한민국 해양수산부 ‘항만 및 어항설계 기준·해설(MOF, 2014)’ 등에서는 잔교식 안벽의 예비 설계 방법으로 응답스펙트럼 해석법을 제시하고 있다. 본 해석법은 다자유도계 운동방정식을 단자유도계 운동방정식으로 분리하여 각 모드에 따른 응답을 구한 뒤, 모드 별 응답을 조합하여 다자유도계 구조물의 최대 응답을 구하는 탄성해석 기법이다(CEN, 2005). 본 해석법은 해석이 간편한 장점이 있으며, 다수의 모드를 고려할 수 있으므로 종래부터 교량 및 구조물의 수치해석 기법으로 널리 활용되어 왔다(Su et al., 2006; Taghavi and Miranda, 2010; Yun et al., 2019; Yun and Han, 2021).
기준서에서는 잔교식 구조물의 응답스펙트럼해석 시 지반-말뚝 상호작용을 고려하기 위해 가상고정점 및 지반스프링 방법을 활용하도록 제시하고 있다(PIANC, 2001; PARI, 2009; ASCE; 2014; MOF, 2014). 먼저, 가상고정점 방법은 말뚝을 등가 고정단 길이를 갖는 프레임 구조물로 가정하는 방법으로, 정적 수평하중을 받는 지반-말뚝의 응답에 관해 다수의 연구가 수행되어 왔다(Nair et al., 1969; Chen, 1997; Chiou and Chen, 2007). 최근 Yun et al.(2019)은 지진 하중을 받는 잔교식 구조물의 응답스펙트럼해석 시 가상고정점 방법의 적용성을 평가하기 위해 응답스펙트럼해석과 동적원심모형실험을 수행하였다. 실험 및 해석을 비교한 결과, 구조물의 고유주기 및 응답에 큰 차이가 발생하였는데 이는 말뚝을 등가 고정단 길이를 갖는 프레임 구조물로 가정하므로 지반과 말뚝의 동적 응답을 적절히 모사하기 어렵기 때문인 것으로 나타났다. 그러므로 Yun and Han(2021)은 지진 하중을 받는 잔교식 구조물의 응답스펙트럼해석 시 구조물의 응답을 적절히 모사할 수 있는 탄성 지반 스프링 모델을 도출하고자 하였다. 다수의 탄성 스프링 모델을 비교한 결과, Terzaghi(1955) 스프링 모델이 말뚝과 지반의 p-y 특성을 가장 유사하게 모사하는 것으로 나타났으며, Terzaghi(1955) 스프링을 적용하여 응답스펙트럼 해석을 수행하는 경우, 시스템의 고유주기 및 구조물의 동적 응답을 가장 적절하게 모사하는 것으로 나타났다. 그러나 위 연구들은 모두 연직 말뚝이 적용된 잔교식 구조물의 응답스펙트럼해석 시 적절한 모델링 방법을 도출하기 위한 연구로서, 현재까지 경사 말뚝이 설치된 잔교식 구조물의 응답스펙트럼 해석에 관한 연구는 매우 부족한 실정이다.
경사 말뚝이 설치된 잔교식 구조물의 응답스펙트럼해석에 관한 연구가 부족한 이유는 몇몇 기준서에서 내진설계 시 경사 말뚝 설치를 권고하고 있지 않기 때문으로 판단된다. French Seismic Code(AFPS, 1990)에서는 지진 하중에 저항하기 위해 경사 말뚝은 사용하지 않도록 명시하고 있으며, Eurocode(2005)에서는 수평 하중을 지반으로 전달하기 위해 경사말뚝을 사용하지 않도록 권고하고 있다. 또한 대한민국 해양수산부 ‘항만 및 어항설계 기준·해설’에서도 경사말뚝과 상판의 연결부에서 파손이 쉽게 발생할 수 있으므로 경사말뚝의 설치를 지양하도록 하고 있다(MOF, 2019). 이는 과거 경사 말뚝이 적용된 잔교식 구조물 피해 사례에서 경사 말뚝과 상판의 연결부에서 파손이 쉽게 발생하였으므로 경사 말뚝의 설치를 지양하는 것으로 판단된다(Nishizawa et al., 1998; PIANC, 2005; Haskell et al., 2013).
그러나 몇몇 연구자들을 통해 경사 말뚝의 긍정적인 역할에 대한 연구들이 수행되어 오고 있다. Harn(2004)은 과거 지진 시 경사 말뚝의 피해가 공학적인 지식 및 수치해석 기법의 부족으로부터 기인되었으며, 진보된 수치해석기법 및 적절한 설계 방법을 적용하는 경우 긍정적인 성능을 확보할 수 있음을 설명하였다. 또한 Sarkar et al.(2018)은 경사 말뚝의 동적 거동을 평가하기 위해 3차원 수치해석을 수행하였다. 5층의 프레임 구조물로 구성된 구조물의 응답을 비교한 결과, 경사 말뚝 기초가 설치된 구조물에서 연직 말뚝 기초가 설치된 구조물에 비해 약 12~50%응답이 감소한 것으로 나타났다. 또한 잔교식 구조물의 동적원심모형실험을 수행하였던 Yun and Han(2020)에 따르면, 경사 지반에 경사 말뚝이 설치되는 경우 경사 지반 모델에서 최대 가속도, 잔류 변위, 최대 모멘트가 각각 48%, 50%, 84% 감소하는 것으로 나타났다.
결과적으로, 경사말뚝의 영향으로 인해 구조물의 거동이 연직말뚝으로만 구성된 구조물과 크게 달라질 수 있으므로, 구조물의 내진성능을 적절히 평가할 수 있는 모델링 기법이 필요할 것으로 판단된다. 본 연구에서는 경사말뚝이 설치된 잔교식 구조물의 동적원심모형실험을 수행하였고, 실험을 바탕으로 가상고정점 및 지반스프링 방법을 적용하여 응답스펙트럼 해석을 수행하였다. 실험 및 해석을 통해 도출된 구조물의 응답을 비교하여 경사말뚝이 적용된 잔교식 구조물의 모델링 방법에 따른 내진성능을 평가하고자 하였다.
2. 동적원심모형실험 수행
원심모형실험은 구조물을 상사 법칙에 따라 축소시켜 고속으로 회전시키면서 회전 가속도를 부여한 후, 실제 구조물과 같은 응력을 재현시키는 실험기법이다. 본 연구에서는 KAIST 원심모형실험 장비를 활용하여 실험을 수행하였다. KAIST 원심모형실험기는 5m 회전 반경을 가지며, 회대 240g-ton에서 실험을 수행할 수 있다(Kim et al., 2013; Yun et al., 2022). 실험에 사용된 모형토조는 길이, 폭, 높이가 각각 49cm, 49cm, 63cm의 정사각형 Equivalent shear beam box이며, 본 토조의 경우 지반의 움직임과 동일하게 거동하면서 벽체 반사파의 영향을 최소화하는 역할을 한다(Kim et al., 2013; Lee et al., 2013).
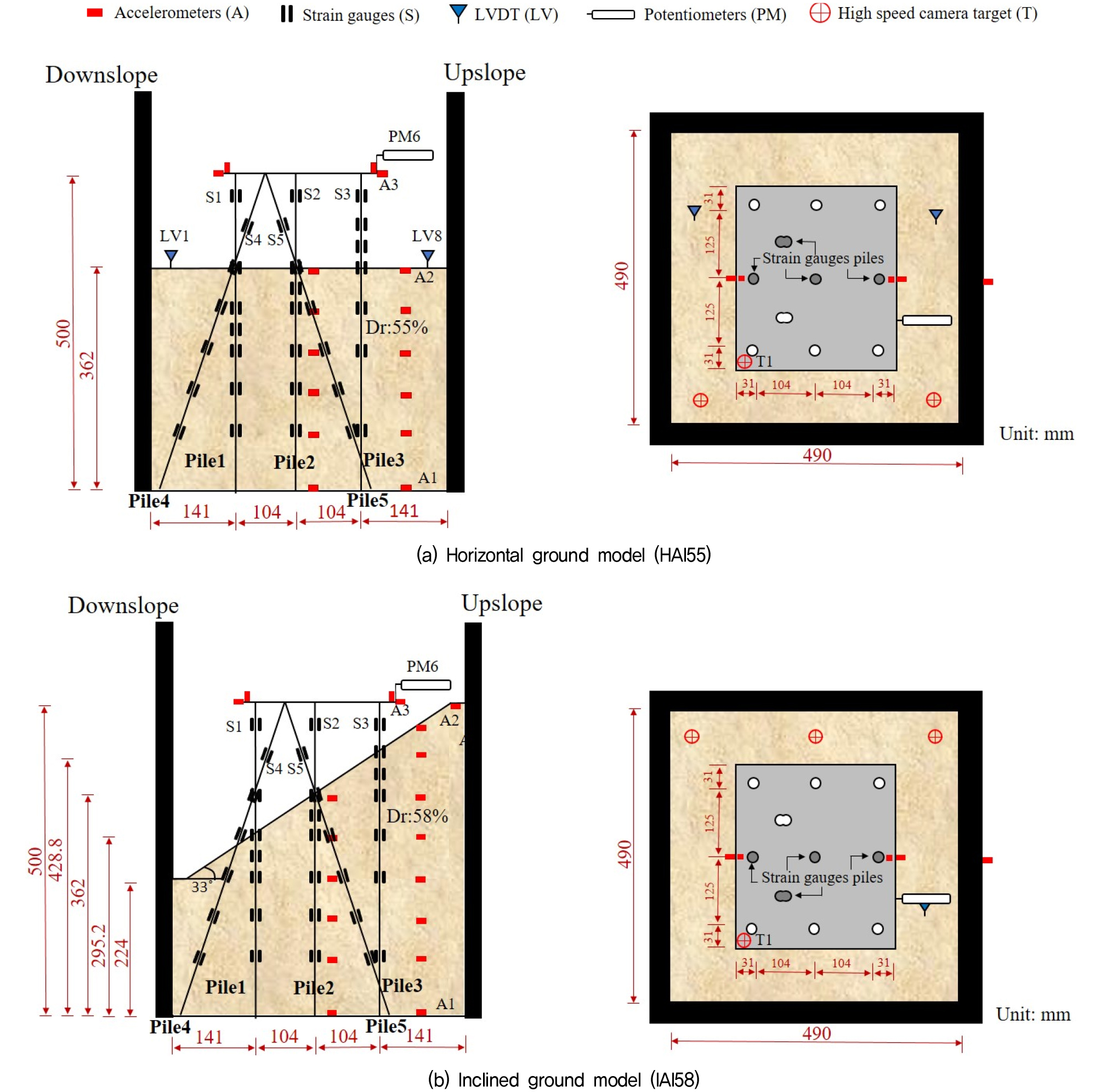
원심모형실험을 위해 대한민국 포항에 위치한 잔교식 구조물 말뚝 중 일부 구간을 선정하였다. 실험 모델의 경우 지반 경사에 따라 Fig. 1과 같이 2가지 모델로 분류하였다. HAI 모델의 경우, Horizontal ground, Artificial input earthquake, 그리고 Inclined pile의 첫 문자를 조합하여 나타내었으며, IAI 모델의 경우, Inclined ground, Artificial input earthquake, 그리고 Inclined pile의 첫 문자를 조합하여 나타내었다. 또한 55 및 58은 지반 상대밀도를 의미한다. 각 모델은 1/48 축소모델로 제작되었으며, 말뚝의 휨강성을 조절하여 모형 제원을 산정하였다. 또한 Table 1과 같이 원형 및 모형 구조물의 상사 법칙을 적용하였으며, Table 2와 같이 모형 말뚝과 플레이트를 알루미늄관(E=68,300Mpa; 포아송비 υ=0.3)으로 제작하였다(McCullough et al., 2007). 스트레인 게이지가 부착된 말뚝의 경우 게이지를 바깥쪽에 붙인 뒤 말뚝 표면을 천공하여 스트레인 게이지 라인을 내부로 관통하였다.
Table 1.
Model scaling factors and values (McCullough et al., 2007)
Table 2.
Prototype and model properties (scale factor=48)
본 실험에서는 지반조성을 위해 인공적으로 생산된 규사(silica sand)를 사용하였으며, 기본 물성정보를 Table 3에 나타내었다. 본 실험은 경사 말뚝이 설치된 잔교식 구조물의 동적 특성을 살펴보기 위한 기초 연구로서, 간극수압을 고려하지 않고 건조토만을 활용하여 지반을 조성하였다. 지반 상대밀도의 경우 낙사법을 활용하여 구현하였으며, 선단지지 말뚝 모사를 위해 말뚝을 하부 플레이트에 고정하였다. 실험을 위해 가속도계, 스트레인게이지, LVDTs, Potentiometers를 설치하였으며, High speed camera를 통해 지진 시 구조물의 거동을 살펴보았다. Fig. 1 및 2에 모형 실험 단면 및 계측기 위치에 대하여 자세하게 나타내었다.
Table 3.
Properties of silica sand
| Soil property | USCS | Cc | Cu | Gs | rd.max (kN/m3) | rd.min (kN/m3) |
| Silica sand | SP | 1.16 | 1.96 | 2.63 | 16.5 | 12.4 |
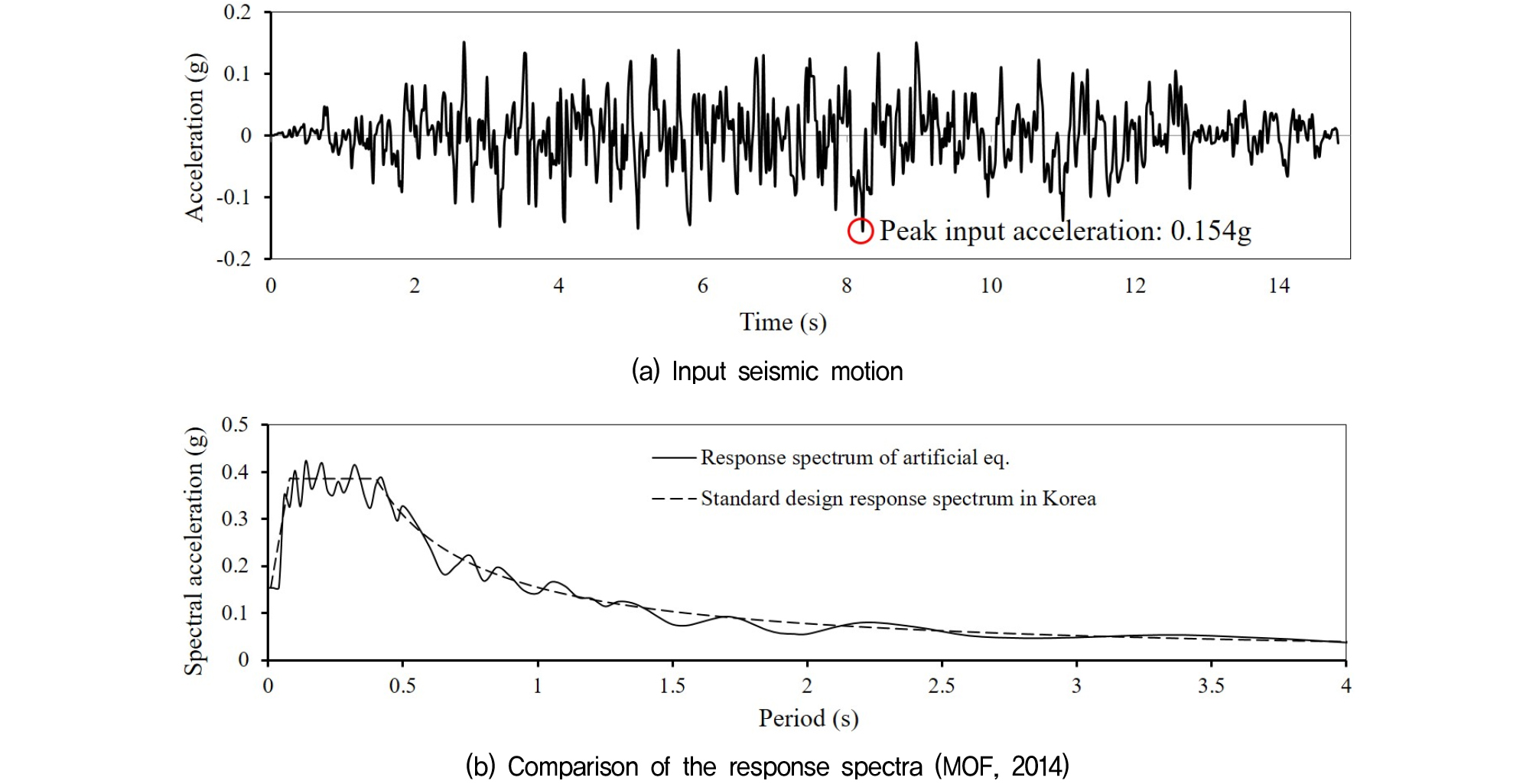
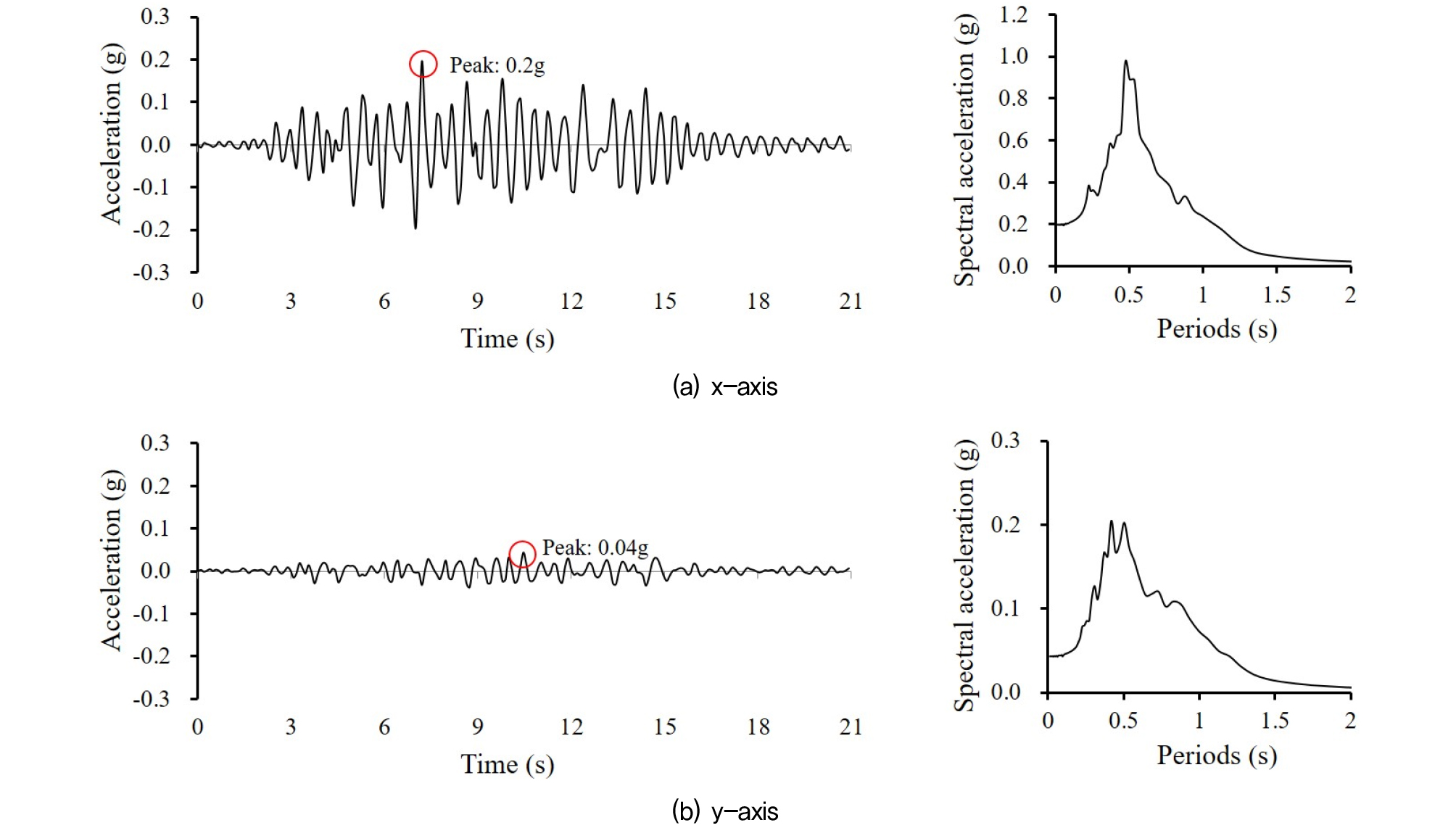
지진파의 경우, 대한민국 해양수산부 ‘항만 및 어항설계 기준·해설’에서 제시하고 있는 대한민국 지반에 적합한 제작 방법에 따라 인공지진파를 Fig. 3(a)와 같이 제작하였다(MOF, 2014). 대한민국 지반에 적합한 특성을 고려한 설계지반 가속도를 기본적으로 응답스펙트럼 곡선으로 표현하며, 일반적으로 5% 감쇠비를 적용하고 있다. Fig. 3(b)에서는 인공지진파의 응답스펙트럼 곡선과 표준설계응답스펙트럼 곡선을 비교하였으며, 두 곡선이 잘 부합함을 알 수 있다. Table 4에서는 각 모델에 적용된 입력지진파의 크기에 대하여 나타내고 있다. 본 실험 모델의 동적원심모형실험 결과는 Yun and Han(2020)에 자세히 설명하고 있다.
3. 응답스펙트럼해석 수행
응답스펙트럼해석은 탄성 동적 수치해석 기법으로, 응답스펙트럼 곡선을 통해 단자유도계 구조물의 응답을 산정하여 모드 조합법을 통해 최대 응답을 도출하는 탄성해석 기법이다(Kiureghian, 1981; Kiureghian and Neuenhofer, 1992; CEN, 2005). 응답스펙트럼 해석에 대한 세부 절차는 연직 말뚝으로 구성된 잔교식 구조물에 대해 응답스펙트럼해석을 수행하였던 Yun and Han(2021)의 연구에서 자세히 설명하였다.
본 절에서는 잔교식 구조물의 응답스펙트럼 해석을 위해 앞서 설명하였던 것과 같이 말뚝을 가상고정점이 적용된 프레임 구조물 및 탄성 지반 스프링으로 지지되는 프레임 구조물로 모델링하였다. 응답스펙트럼 해석을 위해 유한요소 해석 프로그램인 MIDAS GEN 2016 ver. 1.4를 활용하였다(MIDAS, 2016).
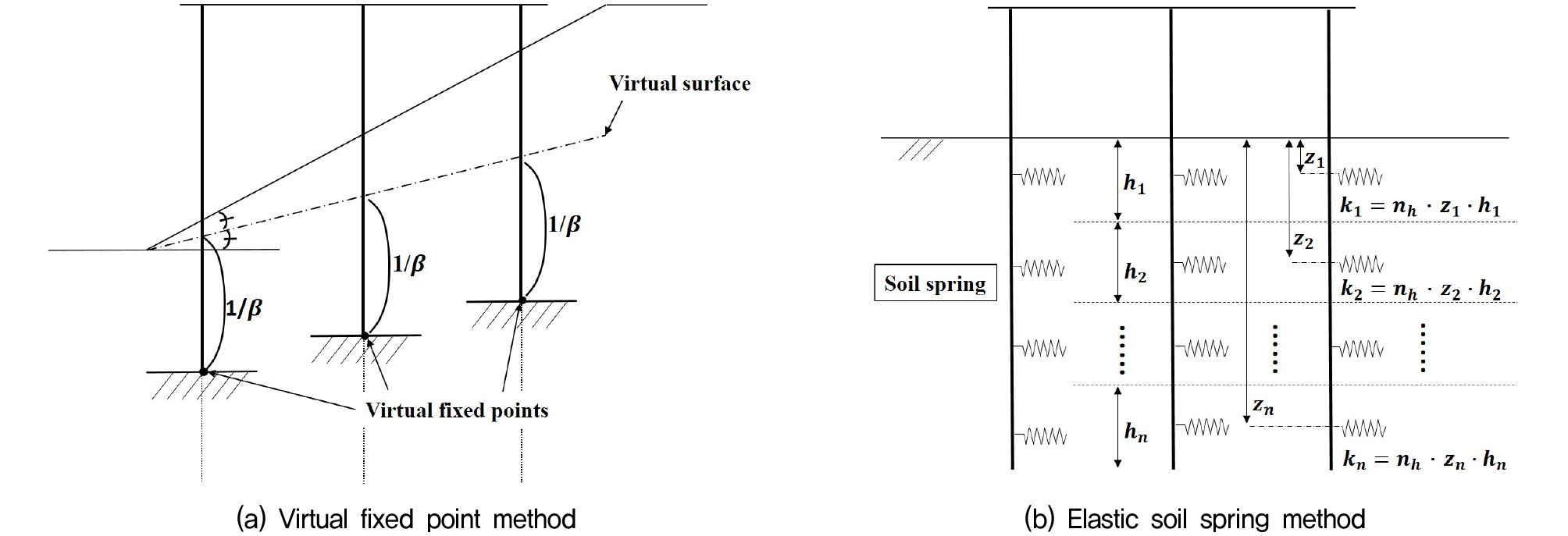
먼저, 가상고정점 방법을 적용하기 위해서는 잔교가 설치된 지반의 경사면 각도 1/2에 해당하는 위치를 가상지표면(virtual surface)으로 가정하여야 하며, 가상지표면 아래 1/β 지점에 가상고정점(virtual fixed point)이 위치한다고 가정하여 Fig. 4(a)와 같이 말뚝을 설계한다. 가상고정점을 산정하기 위해 식 (1) 및 식 (2)를 활용할 수 있다. 여기서, kh는 수평지반반력계수(N/cm3), D는 말뚝 직경(cm), EI는 말뚝의 휨강성(N·cm2), N은 표준관입시험을 통한 지반의 1/β 부근까지의 평균 타격 횟수를 일컫는다(PIANC, 2001).
Meyerhof(1956)는 상대밀도와 N 값과의 상관관계를 도출한 바 있는데, 본 연구에서는 이를 활용하여 지반 상대밀도를 N 값으로 환산하였으며, 수평지반 반력계수 및 가상고정점 값을 산정하였다(Table 5). 본 연구에서는 Fig. 5와 같이 각 모델에 따라 산정된 가상고정점을 활용하여 해석을 수행하였다.
Table 5.
Relationship between the relative density and N value (Meyerhof, 1956)
| Consistency | Very loose | Loose | Medium | Dense | Very dense |
| Relative density | < 0.2 | 0.2-0.4 | 0.4-0.6 | 0.6-0.8 | > 0.8 |
| N value | < 4 | 4-10 | 10-30 | 30-50 | > 50 |
다음으로 지반스프링 방법을 적용하기 위해서는 지반에 관입된 말뚝의 지반 반력을 고려하여 말뚝을 지반 스프링이 적용된 프레임 구조물로 모델링하여야 한다(PIANC, 2001). 여기서, 탄성지반 스프링 강성은 지반반력상수(nk)에 스프링이 위치하는 깊이(z)와 각 지층의 두께(h)를 곱하여 Fig. 4(b)와 같이 산정할 수 있다. Table 6에서는 Yun and Han(2021)이 상대밀도에 따라 정리한 각 스프링 모델의 지반반력 상수(nh)를 비교하여 나타내었다. Yun and Han(2021)은 Terzaghi(1955), Dvisson(1970), API(2000)가 제시한 지반 반력상수를 활용하여 깊이 별 스프링 강성을 도출하였으며, 이를 바탕으로 응답스펙트럼 해석을 수행한 바 있다. 위 연구에 따르면, Terzaghi(1955) 스프링 모델을 적용하는 경우 잔교식 구조물의 고유주기 및 말뚝 모멘트를 가장 적절히 모사하는 것으로 나타났으므로, 본 연구에서도 Terzaghi(1955) 스프링 모델을 적용하여 구조물을 모델링하여 응답스펙트럼 해석을 수행하였다. 본 연구에서는 상용 프로그램으로 MIDAS GEN 2016. ver.1.4를 활용하였다.
Table 6.
Constant of horizontal subgrade reaction (nh) value
| Relative density of sand (%) | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| Terzaghi (1955) (kN/m3) | 1,280 | 2,560 | 4,490 | 7,690 | 12,820 | 19,230 | 25,640 |
| Davisson (1970) (kN/m3) | 7,600 | 10,040 | 12,480 | 14,920 | 17,360 | 19,800 | 22,250 |
| API (2000) (kN/m3) | 2,630 | 6,570 | 12,330 | 25,930 | 43,200 | 58,890 | 75,230 |
또한 지진 시 지반 증폭현상이 발생할 수 있으므로, 응답스펙트럼 해석 시 이를 고려하여 증폭된 지진파를 입력지진파로 적용하여야 한다. Yun 등(2020)은 잔교식 구조물의 응답스펙트럼 해석 시 적절한 입력가속도 결정 방법을 도출하기 위한 연구를 수행하였으며, 경사면 중앙 상부에서 증폭된 지진파를 활용하여 해석을 수행하는 것이 실험에서 도출된 모멘트를 가장 적절히 모사함을 설명하였다. 또한 지표면 상부에서 증폭된 지진파를 활용하여 해석을 수행하는 경우 보수적인 응답이 도출됨을 설명하였다. 그러므로 본 연구에서는 경사면 중앙 상부에서 증폭된 지진파를 활용하여 해석을 수행하고자 하였다.
4. 경사말뚝이 적용된 잔교식 구조물의 동적 거동 분석
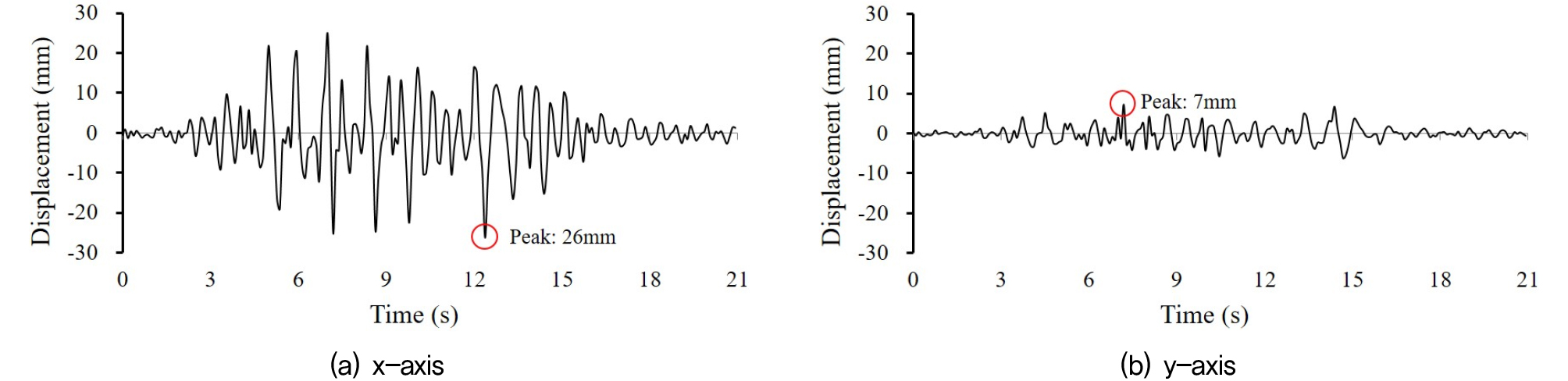
본 실험에서는 시간에 따른 구조물의 거동을 분석하기 위해 Fig. 1과 같이 실험 모델에 high speed camera target을 설치하였으며, 고성능 카메라를 통해 slow-motion movie를 촬영하여 이미지 해석을 수행하였다. 구조물 상단에 설치된 target의 변위를 추적하기 위해 사용프로그램인 TEMA ver. 3.5를 활용하였으며, Fig. 6과 같이 x축 및 y축의 변위 시간이력곡선을 각각 도출하였다. 또한 도출된 변위 시간이력곡선을 두 번 미분하여 x축 및 y축 가속도 시간이력곡선을 도출하였다(Fig. 7). 실험 응답은 모두 원형으로 환산하여 보여주고 있으며, 대표적으로 HAI55(bedrock input peak acceleration: 0.26g) 모델의 응답을 보여주고 있다.
Fig. 6을 보면 구조물 상단(Fig. 1(a)의 T1)에서 x축 방향으로 최대 변위가 약 26mm 발생하였으며, y축 방향으로 최대 변위가 약 7mm 발생하였다. 또한 Fig. 7을 보면 x축 방향으로 최대 가속도가 0.2g 발생하였으며, y축 방향으로 최대 가속도가 0.04g 발생하였다. 본 실험에서는 Fig. 2와 같이 x축 방향으로만 하중을 가력하였음에도 불구하고 y축에서 x축에 비해 28%의 최대 변위가 발생하였으며, 22%의 최대 가속도가 발생한 것으로 나타났다. 또한 가속도 응답스펙트럼 곡선을 보면, x축 및 y축 응답 모두 유사한 주기 영역인 0.47s 부근에서 가장 큰 스펙트럴 가속도 값이 도출되었다.
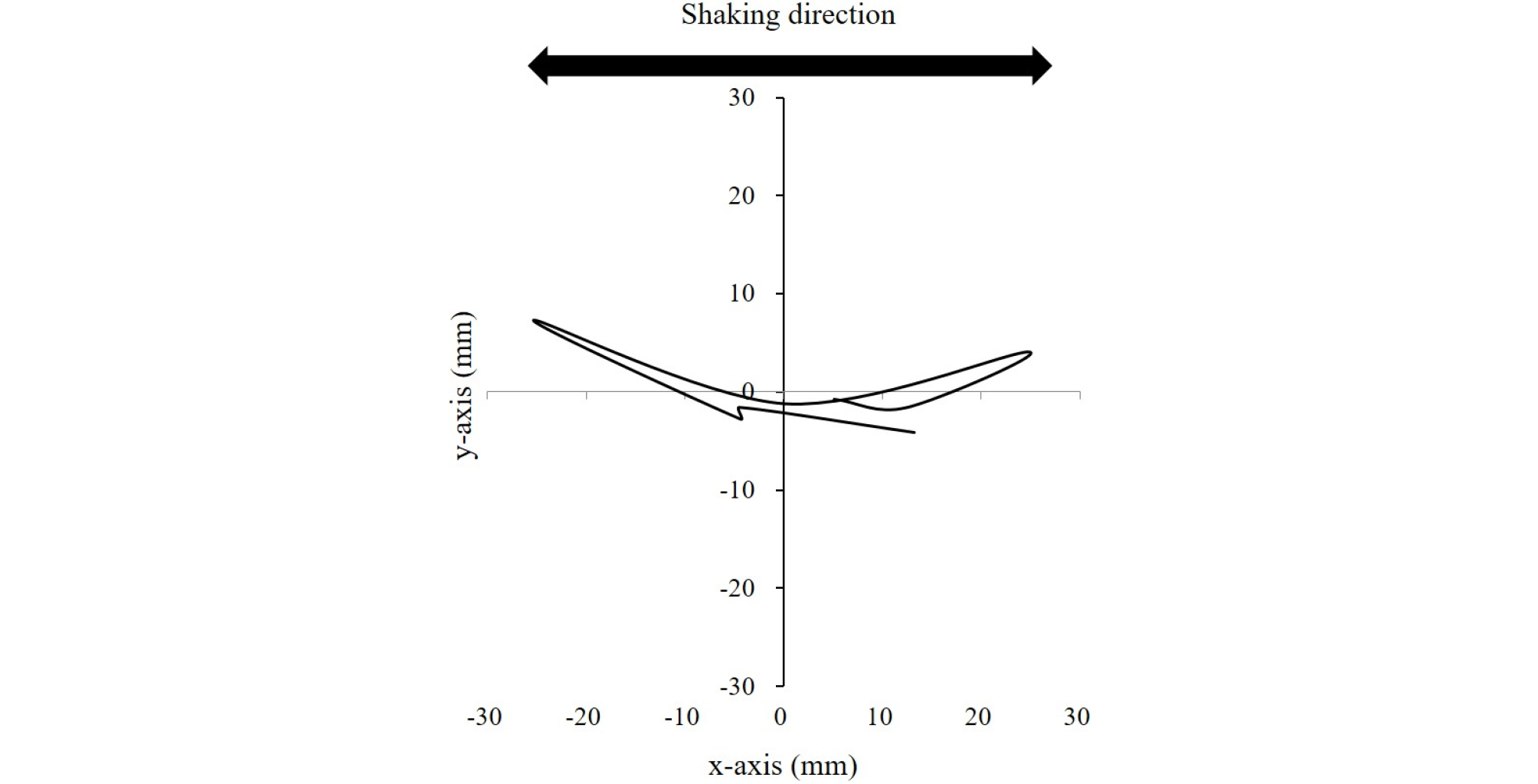
Fig. 8에서는 구조물의 응답이 크게 발생한 6.8-7.5s 사이의 x축 및 y축 변위 응답을 비교하여 보여주고 있다. 그림을 보면, y축에서 x축에 비해 30% 정도의 최대 변위가 발생하였으며, x축 방향으로만 하중을 가력하였음에도 불구하고 실험 모델에 회전이 발생한 것으로 나타났다. 이는 Fig. 1과 같이 구조물 측면에 경사 말뚝이 설치되어 있으며, 스트레인 게이지가 부착된 말뚝 및 부착되지 않은 말뚝에 천공으로 인한 강성 차이가 발생하므로(Table 2), 강성의 비대칭으로 인해 회전이 발생한 것으로 판단된다. 위 결과를 종합적으로 고려해 볼 때, x축 방향으로만 하중을 가력하였음에도 구조물에 회전이 발생하였으며, x축 및 y축 모두 최대 응답이 발생하는 고유주기가 유사하게 도출되었으므로 구조물의 회전 시 회전 방향 고유주기가 0.47s로 도출된 것으로 판단된다.
본 절에서는 구조물의 회전 거동을 명확히 살펴보기 위해 실험 모델을 다자유도계 구조물로 모사하여 고유치해석을 수행하였다. 해석 모델의 경우 앞서 3장에서 설명하였던 가상고정점 모델 및 Terzaghi(1955) 수평지반반력상수(nh)를 적용한 지반스프링 모델을 활용하였다. 고유치해석은 다자유도계 구조물에 대한 미분 방정식 해를 구하기 위한 일련의 과정으로, 각 진동모드에 따른 모드 형상을 간편하게 구할 수 있는 기법이다(Wilkinson, 1965). 본 연구에서는 고유치 해석을 통해 각각의 고유 모드에 따른 고유주기를 도출하였으며, 해석을 위해 상용프로그램인 MIDAS GEN 2016 ver. 1.4을 활용하였다(MIDAS FEA, 2016).
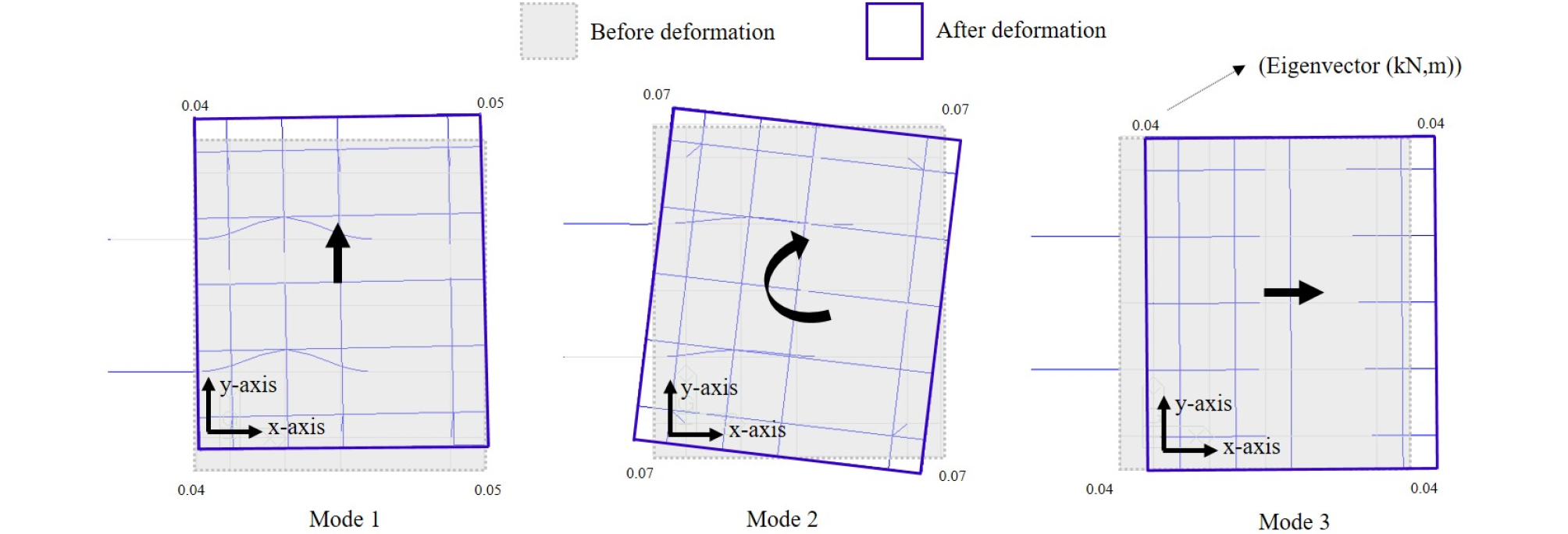
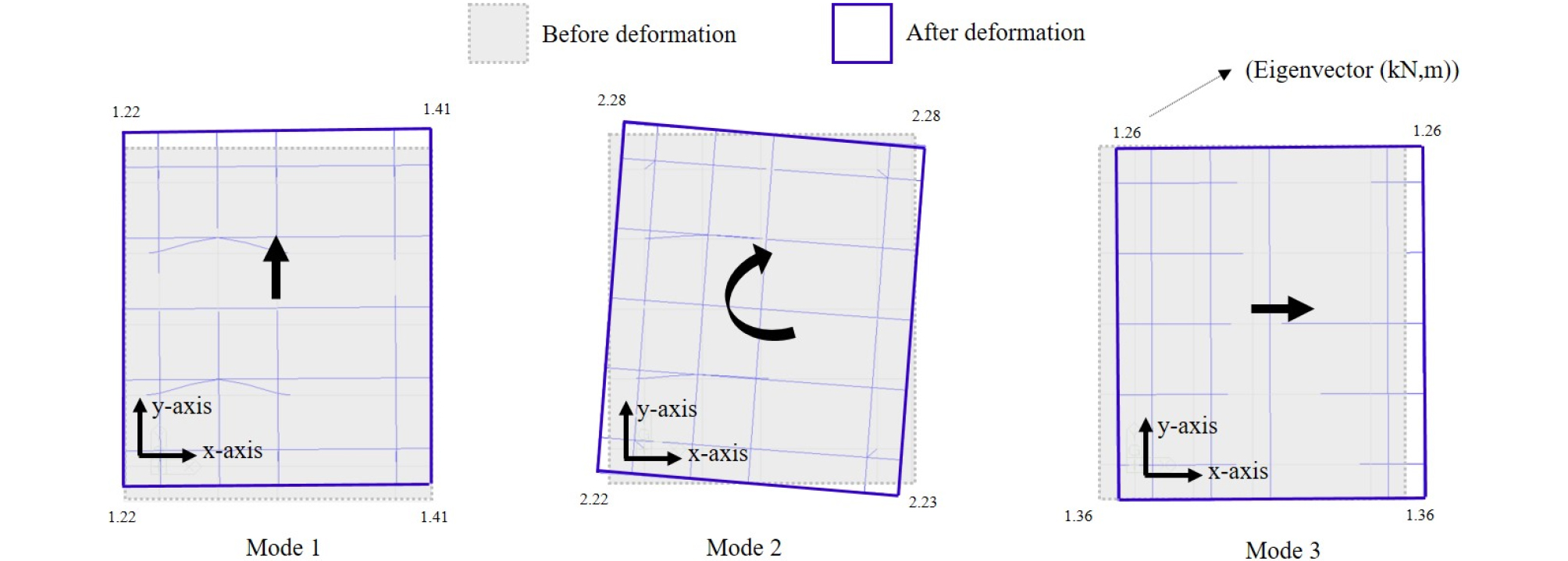
Fig. 9 및 10은 지반스프링 및 가상고정점 방법으로 모델링 한 HAI55 모델의 고유 모드에 따른 모드 형상을 대략적으로 나타내고 있으며, 실제 변형을 명확히 살펴보기 위해 약 25배 스케일로 확대하여 나타내었다. 또한 Table 7 및 8에서는 지반스프링 모델 및 가상고정점 모델의 고유 모드에 따른 질량참여계수와 고유주기를 나타내고 있다. 질량참여계수는 각 모드가 응답에 참여하는 정도를 나타내며, 질량참여계수가 클수록 구조물의 응답에 지배적인 역할을 하는 것을 알 수 있다.
Table 7.
Mode participation mass and natural periods according to the natural mode (soil spring model)
| Modal participation mass (%) | Natural periods (s) | |||
| Tran. -X | Tran. -Y | Rot. - Z | ||
| Mode 1 | 0.0 | 88.4 | 1.2 | 0.54 |
| Mode 2 | 0.9 | 1.1 | 85.9 | 0.44 |
| Mode 3 | 89.3 | 0 | 1.0 | 0.34 |
| Mode 4 | 0.9 | 0 | 0 | 0.08 |
| Mode 5 | 0 | 0 | 0 | 0.08 |
Table 8.
Mode participation mass and natural periods according to the natural mode (virtual fixed point model)
| Modal participation mass (%) | Natural periods (s) | |||
| Tran. -X | Tran. -Y | Rot. - Z | ||
| Mode 1 | 0.0 | 97.0 | 0.4 | 0.44 |
| Mode 2 | 0.1 | 0.4 | 96.7 | 0.34 |
| Mode 3 | 97.3 | 0 | 0.1 | 0.23 |
| Mode 4 | 0 | 0 | 0 | 0.05 |
| Mode 5 | 0 | 0 | 0 | 0.05 |
먼저 지반스프링 모델(Fig. 9, Table 7)을 보면, Mode 1에서는 y축 방향의 질량 참여계수가 88.4%로서, 구조물의 y축 거동이 지배적인 것을 알 수 있으며, 이때의 고유 주기는 0.54s로 도출되었다. Mode 2에서는 회전 방향의 질량참여계수가 85.9%로서 구조물의 회전 방향 거동이 지배적인 것을 알 수 있으며, 이때의 고유주기는 0.44s로 도출되었다. Mode 3에서는 x축 방향의 질량참여계수가 89.3%로서 구조물의 x축 거동이 지배적인 것을 알 수 있으며, 이때의 고유주기는 0.34s로 도출되었다. 고유치 해석은 구조물에 가해지는 외력과 감쇠가 없다고 가정하며, 초기 변위를 주어 구조물의 고유 진동 모드를 산정하는 방법이다. 본 해석 모델의 경우, 경사 말뚝이 x축과 나란히 설치되어 x축 방향 저항력이 크게 증가하였으므로, y축 방향으로 1차 모드가 도출된 것으로 보인다. 그러나 본 실험모델에서는 x축 방향으로만 하중을 가력하였으므로 y축 방향으로 거동하는 1차 모드의 영향이 거의 없으며, 회전 거동을 하는 2차 모드가 구조물의 거동에 더 큰 영향을 미칠 수 있는 것으로 판단된다. 실험을 통해 도출된 구조물의 회전방향 고유주기 및 고유치 해석으로 도출된 2차 모드의 고유주기를 비교해 보면 각각 0.47s, 0.44s로 도출되어 실험 및 지반스프링 모델의 고유주기가 유사한 것으로 나타났다.
다음으로 가상고정점 모델(Fig. 10, Table 8)을 보면, Mode 1에서는 y축 방향의 질량참여계수가 97.0%로서 구조물의 y축 거동이 지배적인 것을 알 수 있으며, 이때의 고유 주기는 0.44s로 도출되었다. Mode 2에서는 회전 방향의 질량참여계수가 96.7%로서 구조물의 회전 방향 거동이 지배적인 것을 알 수 있으며, 이때의 고유주기는 0.34s로 도출되었다. Mode 3에서는 x축 방향의 질량참여계수가 97.3%로서 x축 거동이 지배적인 것을 알 수 있으며, 이때의 고유주기는 0.23s로 도출되었다. 지반스프링 모델과 가상고정점 모델의 질량참여계수는 비교해 보면, 지반스프링 모델의 경우 대부분 Mode 1~3 질량참여율이 각각 80% 후반으로 도출되었는데, 가상고정점 모델의 경우 90% 후반으로 도출된 것을 알 수 있다. 이는 가상고정점 모델의 경우 하부 말뚝이 짧고 고정단으로 구성되어 있어 자유도가 작으므로, 저차 모드에서 구조물의 거동이 결정되기 때문이다. 또한 가상고정점 모델의 경우 하부 말뚝이 짧고 고정단으로 구성되어 있으므로 지반스프링 모델에 비해 고유주기가 작게 도출된 것으로 판단된다.
본 결과를 통해 경사말뚝이 적용된 잔교식 구조물의 경우 Terzaghi(1955) 수평지반반력상수를 활용한 스프링 방법 적용 시 구조물의 고유주기를 적절히 모사할 수 있는 것으로 판단된다. 또한 경사 말뚝이 설치된 잔교식 구조물의 경우 구조물의 비대칭성으로 인해 회전이 발생할 수 있으므로, 하나의 모드만을 고려할 수 있는 단일모드 스펙트럼해석보다 회전방향 고유모드가 포함된 다수의 모드를 고려할 수 있는 다중모드 스펙트럼해석을 통해 설계를 수행하는 것이 적절할 것으로 판단된다.
5. 경사말뚝이 적용된 잔교식 구조물의 응답스펙트럼 해석
본 연구에서는 Terzaghi(1955) 지반 스프링 방법 및 가상고정점 기법을 활용하여 응답스펙트럼 해석을 수행하였으며, 이를 동적원심모형실험과 비교하여 모델링 방법에 따른 잔교식 구조물의 내진성능을 평가하였다.
연직 말뚝으로 구성된 잔교식 구조물의 경우 지진, 파랑 및 충격력 등의 수평하중에 의해 말뚝에 큰 손상이 발생할 수 있으므로 설계 시 말뚝의 휨 성능을 적절히 평가하는 것이 매우 중요하다. 그러나 경사 말뚝이 설치된 잔교식 구조물의 경우, 수평 하중을 축력으로 전달하여 큰 축력 또한 발생하므로 모멘트 뿐 아니라 축력까지 고려해주어야 한다(Yun and Han, 2020). 그러므로 본 연구에서는 동적원심모형실험 및 응답스펙트럼해석으로 도출된 말뚝의 모멘트와 축력을 중점적으로 비교하였다.
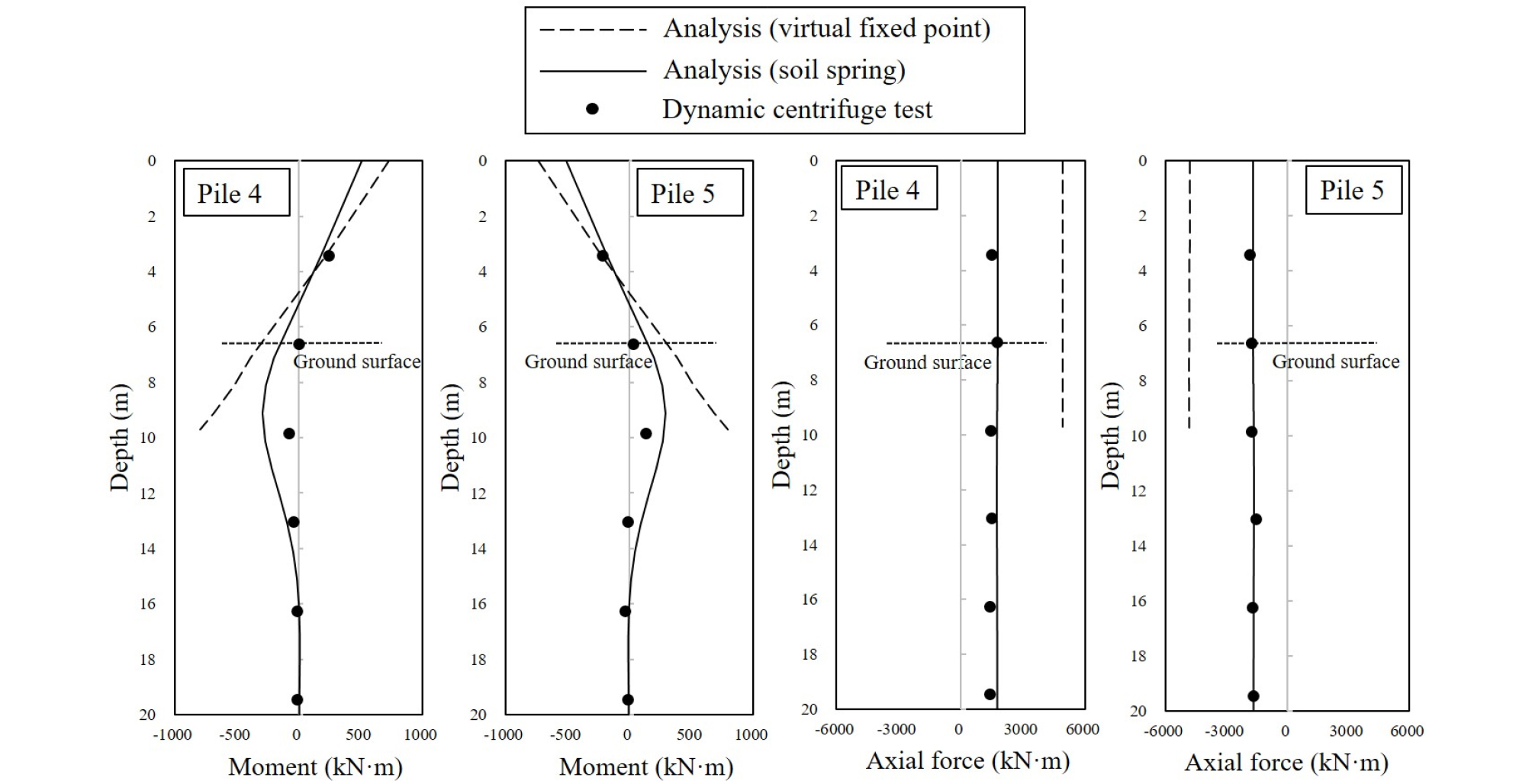
Fig. 11 및 Fig. 12에서는 수평지반 잔교식 구조물(HAI55 model, bedrock input peak acceleration : 0.26g)에서 수행된 실험 및 해석의 깊이 별 말뚝 모멘트 및 축력을 비교하여 나타내고 있다. Fig. 11은 연직 말뚝의 깊이 별 모멘트 결과를, Fig. 12는 경사 말뚝의 깊이 별 모멘트 및 축력을 보여주고 있다. 그래프에서는 가상고정점 방법 및 지반스프링 방법을 활용한 응답스펙트럼 해석 결과를 나타내고 있으며, 실험을 통해 말뚝 별 최대 응답이 발생한 시점의 깊이 별 응답을 함께 나타내었다. 본 그래프에서 Pile 1 상단 및 Pile 3 하단 실험 모멘트의 경우 계측기의 오류로 계측되지 못하였다.
먼저, 가상고정점 기법이 적용된 응답스펙트럼 해석 결과와 실험 결과를 비교해 보면, 깊이 별 모멘트 결과에 큰 차이가 있음을 알 수 있다. Fig. 11 및 연직 말뚝(Pile 1~3) 실험 결과의 경우 음(-) 방향 최대 모멘트가 말뚝 상부에서 발생하며, 말뚝 하부로 갈수록 양(+) 방향으로 증가하다가 약 10m 깊이에서 양(+) 방향 최대 모멘트가 발생한 뒤, 16m 부근에서 0으로 수렴하게 된다. 반면, 해석 모델의 연직 말뚝(Pile 1~3) 깊이 별 모멘트를 보면, 모멘트가 직선 형태로 도출되었는데, 이는 말뚝 하부를 고정단으로 모사하였기 때문에 하부 고정단에서 최대 모멘트가 발생한 것으로 판단된다. 다음으로 Fig. 12 경사 말뚝(Pile 4~5) 깊이 별 축력을 비교해 보면, 마찬가지로 실험 및 해석으로 도출된 축력에 큰 차이가 있음을 알 수 있다. 깊이에 따라 유사한 축력이 도출되었으나, 해석에서 실험에 비해 매우 큰 축력이 도출된 것으로 보인다. 또한 실험 모델의 경우 스트레인 게이지가 부착된 20m 깊이까지 응답이 계측되었으나, 가상고정점 모델의 경우 Fig. 5와 같이 말뚝 길이가 짧게 모사되므로 약 10m 깊이까지의 응답이 도출되었다. 결과적으로, 가상고정점 방법을 활용하여 응답스펙트럼 해석을 수행하는 경우 실험과 큰 차이가 발생하였다.
또한 Fig. 11 및 Fig. 12에는 Terzaghi(1955) 지반 스프링 모델이 적용된 응답스펙트럼 해석 결과와 실험 결과를 비교하여 나타내고 있다. 먼저, 연직 Fig. 11 연직 말뚝(Pile 1~3) 깊이 별 모멘트를 비교해 보면, 지반 스프링 모델을 적용하는 경우 가상고정점 모델에 비해 깊이 별 모멘트를 적절히 모사하는 것을 알 수 있다. 또한 Fig. 12 경사 말뚝(Pile 4~5) 깊이 별 축력을 비교해 보면, 깊이에 따라 유사한 축력이 도출되었으며, 실험 및 해석으로 도출된 축력이 유사한 것으로 보인다. 본 결과를 통해 경사 말뚝이 설치된 잔교식 구조물의 경우에도 Terzaghi(1955) 스프링을 적용하여 응답스펙트럼 해석을 수행하는 것이 구조물의 고유주기 및 모멘트, 축력 응답을 적절히 모사하는 것으로 판단된다.
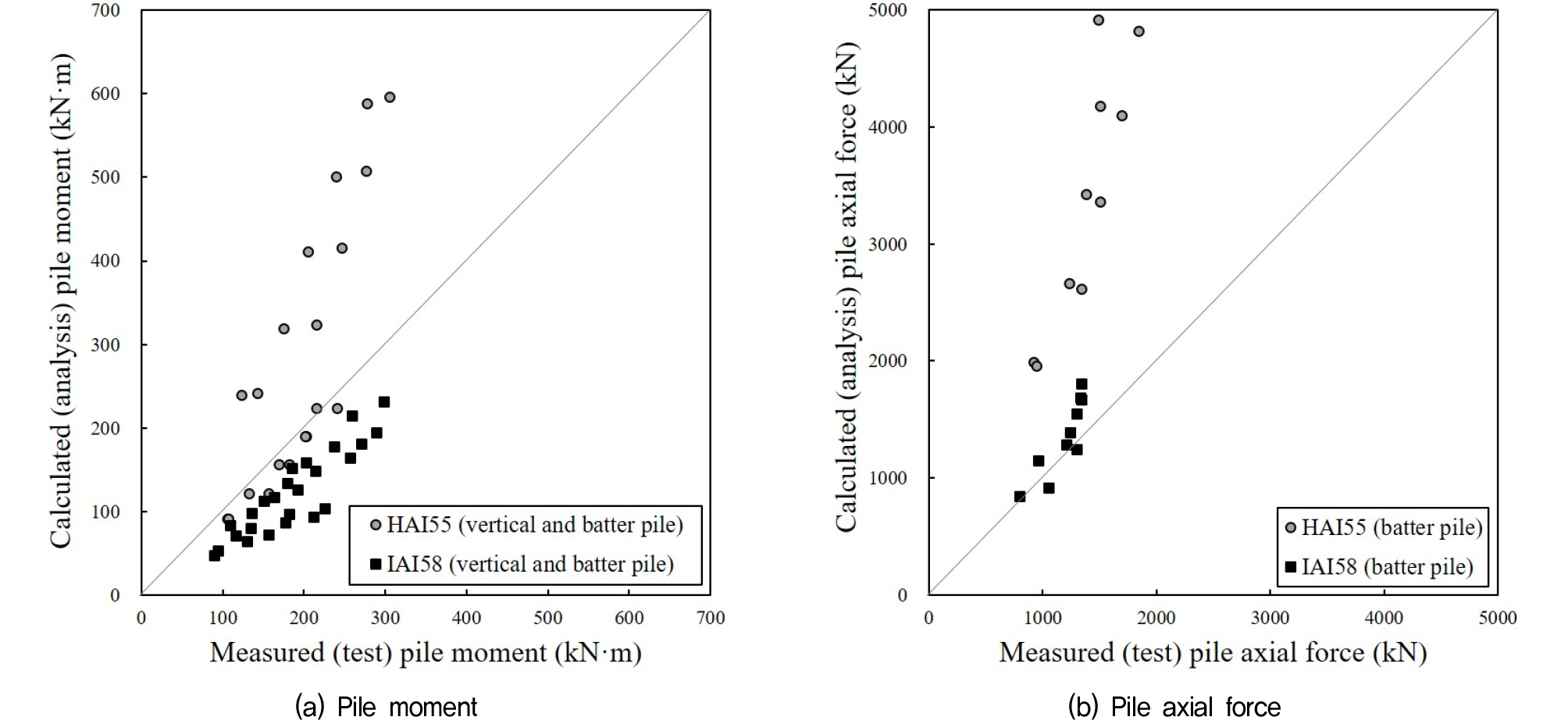
Fig. 13 및 14에서는 본 연구에서 수행하였던 전체 실험 및 해석으로 도출된 말뚝 최대 모멘트 및 축력 결과를 비교하여 나타내었다. 모멘트의 경우 연직 및 경사 말뚝 상부(1.62m 깊이) 응답을 도출하였으며, 축력의 경우 경사 말뚝 상부(3.42m 깊이) 응답을 도출하였다. 먼저 Fig. 13에서는 가상고정점 방법을 활용한 응답스펙트럼 해석 결과를 실험 결과와 비교하였다. 그림을 보면, 해석 모델에서 수평 지반 모델(HAI55)의 모멘트 및 축력이 모두 크게 도출된 것으로 나타났다. 특히 해석 모델에서 4913kN의 축력이 발생하였는데, 이는 실험 모델에서 도출된 축력인 1492kN보다 약 3배 정도로 큰 것으로 보인다. 결과적으로, 가상고정점 방법을 활용하여 응답스펙트럼 해석을 수행하는 경우 실험과 큰 차이가 발생하였는데, 이는 가상고정점 및 실험 모델의 말뚝 길이 차이에 따른 고유주기 차이로 판단된다. 수평지반 모델에 가상고정점 방법을 적용하는 경우 Fig. 5(a)와 같이 지반에 관입된 말뚝 길이를 매우 짧게 모사하므로, 고유 주기 차이가 발생하게 되고, 이로 인해 구조물에 발생하는 응답에 차이가 발생할 수 있기 때문이다. 연직 말뚝으로 구성된 잔교식 구조물의 응답스펙트럼 해석을 수행하였던 Yun et al.(2022)에 따르면, 특정 지진에 의해 구조물이 받는 응답은 구조물의 고유주기에 따라 변하므로, 구조물의 고유주기에 차이가 발생하는 경우 구조물의 응답 또한 차이가 발생할 수 있음을 설명하였다.
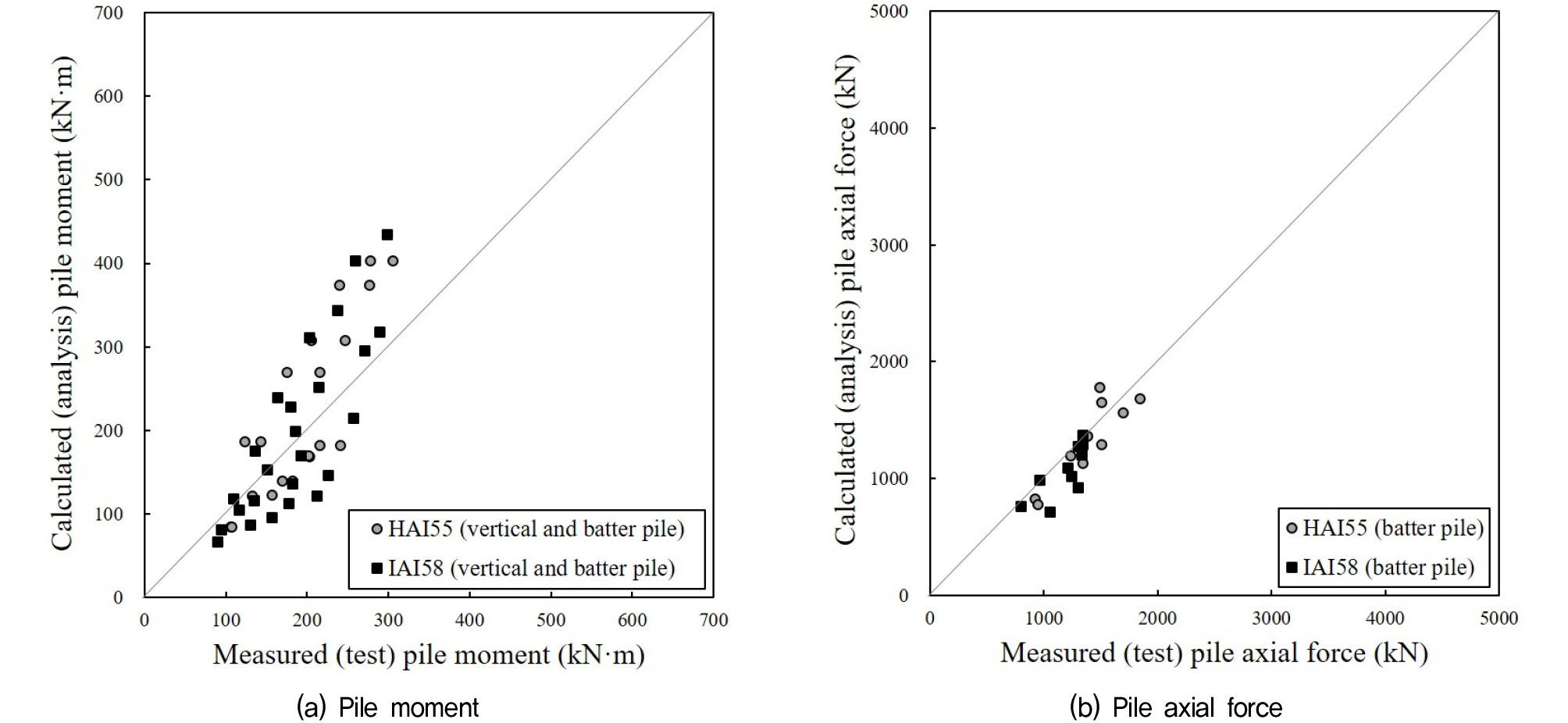
다음으로 Fig. 14에서는 Terzaghi(1955) 지반 스프링 기법을 활용한 응답스펙트럼 해석 결과를 실험 결과와 비교하였다. 그림을 보면 가상고정점 방법이 적용되는 경우에 비해 모멘트와 축력을 적절히 모사하는 것으로 보인다. 이는 지반 스프링 모델의 경우 지반에 관입된 말뚝 길이를 실제 말뚝과 유사하게 모사하므로 구조물의 고유주기를 적절히 모사할 수 있게 되고, 결과적으로 말뚝에 발생하는 응답 또한 적절히 모사할 수 있기 때문으로 판단된다.
결과적으로, 경사말뚝이 설치된 잔교식 구조물에 가상고정점 기법을 적용하여 응답스펙트럼 해석을 수행하는 경우, 깊이에 따른 구조물의 응답을 적절히 모사하기 어려우며, 상당히 보수적인 모멘트 및 축력 값이 도출 될 수 있는 것으로 나타났다. 반면, Terzaghi(1955) 지반 스프링 기법을 적용하여 응답스펙트럼 해석을 수행하는 경우 깊이에 따른 구조물 응답을 적절히 모사하는 것으로 나타났으며, 가상고정점 기법에 비해 실험과 유사한 응답이 도출되는 것으로 나타났다.
본 연구는 경사 말뚝이 설치된 잔교식 구조물의 내진성능 평가를 위한 기초 연구로서, 간극수압을 고려하지 않고 건조토만을 활용하여 지반을 조성하였다. 그러나 실제 잔교식 구조물의 경우 간극수압이 발생하는 포화지반에 관입되어 있으며, 지진 시 과잉간극수압의 증가로 인해 지반의 운동학적 힘이 증가할 수 있는 것으로 알려져 있다. 그러므로 향후 포화된 지반-말뚝 상호작용 및 지반의 운동학적 힘을 고려한 수치해석 기법의 도출이 필요할 것으로 판단된다.
6. 결 론
본 연구에서는 경사말뚝이 설치된 잔교식 구조물의 모델링 방법에 따른 내진성능을 평가하기 위해 동적원심모형실험과 더불어 응답스펙트럼해석을 수행하였다. 동적원심모형실험 모델의 경우 지반 경사에 따라 2가지 모델(수평, 경사)로 분류하였으며, 실험 모델에 가상고정점 및 지반스프링 방법을 적용하여 응답스펙트럼해석을 수행하였다. 실험 및 해석을 통해 도출된 구조물의 응답을 비교하였으며, 경사말뚝이 적용된 잔교식 구조물의 모델링 방법에 따른 내진성능을 평가하였다. 본 연구를 통해 얻어진 결론은 다음과 같다.
(1) 경사 말뚝이 설치된 잔교식 구조물의 회전 거동을 분석하기 위해 지반 스프링 기법을 활용하였으며, 실험 모델을 다자유도계로 모사하여 고유치 해석을 수행하였다. 실험 및 해석을 통해 도출된 구조물의 회전 방향 고유주기가 0.47s, 0.44s로 도출되어 실험 및 해석의 고유주기가 유사함을 확인하였다. 본 결과를 통해 경사 말뚝이 설치된 잔교식 구조물의 경우 Terzaghi(1955)의 지반반력상수(nh)를 활용한 지반 스프링 방법을 적용하는 것이 구조물의 고유주기를 적절히 모사할 수 있는 것으로 나타났다.
(2) 경사 말뚝이 설치된 잔교식 구조물의 경우 구조물의 비대칭성으로 인해 회전이 발생할 수 있으므로, 하나의 모드만을 고려하는 단일모드 스펙트럼해석보다 회전 방향 고유 모드가 포함된 다수의 모드를 고려할 수 있는 다중모드 스펙트럼 해석을 통해 설계를 수행하는 것이 적절할 것으로 판단된다.
(3) 경사말뚝이 적용된 잔교식 구조물 내진성능 평가를 위해 가상고정점 및 지반스프링 기법을 활용하여 응답스펙트럼해석을 수행하였다. 가상고정점 기법을 활용하여 응답스펙트럼 해석을 수행하는 경우, 말뚝 모멘트 및 축력 응답을 적절히 모사하지 못하는 것으로 나타났다. 이는 가상고정점 방법을 적용하는 경우 지반에 관입된 말뚝 길이를 매우 짧게 모사하므로, 고유 주기 차이가 발생하게 되고, 이로 인해 구조물에 발생하는 응답에 차이가 발생할 수 있기 때문이다.
(4) 반면, Terzaghi(1955) 지반스프링 방법을 적용하여 응답스펙트럼 해석을 수행하는 경우, 말뚝 모멘트 및 축력 응답을 적절히 모사하는 것으로 나타났다. 이는 지반 스프링 모델의 경우 지반에 관입된 말뚝 길이를 실제 말뚝과 유사하게 모사하므로 구조물의 고유주기를 적절히 모사할 수 있게 되고, 결과적으로 말뚝에 발생하는 응답 또한 적절히 모사할 수 있기 때문으로 판단된다.