1. 서 론
2. 수치해석을 위한 흙막이 해석 단면
2.1 수치해석 지반조건
2.2 수치해석 굴착 규모와 흙막이 벽체 및 지보재 형식
3. 수치해석 모델링
3.1 수치모델 및 해석순서
3.2 입력지진파
3.3 지반요소
3.4 지반물성
3.5 구조체 모델링
3.6 내진해석 모델의 경계조건
4. FLAC 해석 모델링의 적정성 검증
5. 수치해석 결과
6. 지진하중이 흙막이 구조물의 설계에 미치는 영향
6.1 지진하중이 벽체 설계에 미치는 영향
6.2 지진하중이 지보재 설계에 미치는 영향
6.3 지진하중이 띠장 설계에 미치는 영향
7. 결 론
1. 서 론
현재 서울과 경기 등 대도시의 초고밀도 지역을 중심으로 수도권광역급행철도, 영동대로 복합환승센터, 초고층빌딩, 대심도 지하도로 건설공사 등 대형 인프라 시설물을 구축하기 위한 대심도 지하 굴착공사가 증가하고 있다. 과거보다 지하 굴착공사의 규모가 커지고 흙막이 구조물의 존치 기간이 길어지고 있어, 붕괴발생시 주변 건축물의 침하와 균열, 매립시설물의 파손과 같은 재산피해는 물론이고 수많은 인명 피해를 일으킬 수 있다. 따라서 흙막이 시설물의 대형화, 장기화 추세를 고려할 때 기존에는 중요성을 인지하지 못한 지진과 같은 자연재해에 대해서도 철저한 대비가 필요한 상황이다. 그러나 한편으로는 강진이 빈번하게 발생하는 나라들과는 다르게 아직 국내에서는 지진 시 흙막이 시설물의 피해 사례가 보고된 바 없고, 임시 구조물에 대해서도 내진설계를 적용할 경우 발생할 수 있는 공사비 상승과 경제적 효율성의 문제, 그리고 부정적인 사회적 인식도 고려해야만 한다.
최근 대도시의 교통체증 해소와 대심도 안전기준을 강화하기 위한 방안으로 대심도 지하 건설 및 관리에 관한 특별법 제정을 준비하고 있다. 따라서 흙막이 시설물의 내진설계 적용 대상을 합리적으로 선별하고 적정한 기준을 정립해야 할 필요가 있는데, 아직 국내는 물론 해외에서도 흙막이 시설물의 내진설계 기준은 명확하게 정립되어 있지 않으며, 관련 연구사례도 많지 않은 것이 현실이다.
국내 흙막이 시설물에 대한 설계기준에서는 지반 조건 및 활동 전도 등에 대한 안전율, 지반종류에 따른 예상 수동토압과 흙막이 벽의 형식에 따른 허용변위량을 정의하고 있으나, 내진과 관련된 내용은 없는 실정이다(KDS 21 30 00, 2018, KCS 11 19 15, 2019). 미국의 가시설 관련 내진설계 기준에서는 교량의 경우 5년 이상 공사시 영구구조물로 간주하여 내진설계를 적용하고 있다(AASHTO, 2017, ASCE, 2015). 일본의 가시설 관련 내진설계 기준에서는 내진성능을 고려한 시공방법을 정성적으로 제시하였으며, 설치 기간이 길거나 중요구조물에 근접한 경우 내진성능을 고려하고 있다(도로토공-가설구조물공지침, 1999; 터널표준시방서-개삭공법편, 2016). 유럽의 가시설 관련 내진설계 기준으로는 구조물의 붕괴방지, 피해제한 요건 준수에 관한 기준과 흙막이 구조물에 대한 내진설계에 따른 액상화 안정 확보 및 지진계수 적용에 대한 내용이 포함되어 있다(EN 1998-1:2004, EN 1998-5:2004).
이에 본 논문에서는 흙막이 시설물 내진설계의 필요성을 살펴보기 위한 기초 연구로서, 대표적인 흙막이 시설물인 지하연속벽(Diaphragm wall)을 대상으로 유한차분해석 프로그램인 FLAC을 이용하여 동적 수치해석을 수행하고, 지진하중이 흙막이 시설물의 동적 거동에 미치는 영향을 평가하였다. 그리고 지진하중 작용 시 벽체에 발생한 최대 모멘트와 지보재의 최대 축력을 이용하여, 현행 기준에 따라 상시조건에서 설계된 흙막이 시설물의 부재 안정성을 재평가함으로써, 지진하중이 기존 시설물의 안정성(단면 설계)에 미치는 영향을 분석하였다.
2. 수치해석을 위한 흙막이 해석 단면
수치해석에 가장 큰 영향을 미치는 지반조건을 현실적으로 제시하고, 대심도·대규모 굴착 조건에 적합한 흙막이 벽체와 지보재의 형식을 결정하여 내진해석을 위한 합리적인 단면을 설정하고자, 김포-00간 도로건설공사, 00대로 강남권 광역복합환승센터, 00자동차부지 특별계획구역 복합시설 신축사업 관련 자료 등 서울과 경기 대도시를 중심으로 실제 흙막이 시설물이 설계 또는 시공된 사례들을 분석하였다.
2.1 수치해석 지반조건
서울과 수도권 지역의 주요 프로젝트에서 분석한 지층조건을 정리하면 Table 1과 같다. 전반적으로 토사층이 풍화대에 비해 두껍게 존재하고, 기반암의 출현 심도는 4.5∼29.3m까지 다양하게 분포하였다. 국토교통부의 내진설계일반 (17 10 00 : 2018) 기준 적용 시 지반종류는 기반암 심도가 20m 이내일 경우에는 주로 S3 지반, 20m 이상일 경우에는 S4 지반으로 분류되는 것으로 나타났다.
Table 1.
Site conditions of major projects in Seoul / Gyeonggi province
이에 본 수치해석에서는 기반암 심도가 20m 이내와 20m 이상인 두 가지 조건으로 구분하고, 매립층과 퇴적층의 두께를 풍화대보다 크게 가정하였으며, 지반종류가 S3 지반과 S4 지반이 되도록 Table 2와 같이 두 가지의 지층 단면을 결정하였다. 그리고 해석에 영향을 미치는 인자들을 최소화하기 위해, 지진 시 발생하는 과잉간극수압의 영향을 배제하고자 지하수위는 고려하지 않았다.
Table 2.
Site condition for numerical analysis
2.2 수치해석 굴착 규모와 흙막이 벽체 및 지보재 형식
최근 수행된 대규모 굴착 프로젝트들의 터파기 심도와 폭, 그리고 흙막이 벽체와 지보재의 설계 내용을 정리하면 Table 3과 같다.
Table 3.
Earth retaining system of recent deep excavation
굴착 심도는 지반과 접촉한 벽면을 기준으로 약 23.0∼38.8m의 범위를 갖는 것으로 나타났으며, 이에 본 연구에서는 굴착 심도가 얕은 조건(20m)과 깊은 조건(40m)으로 구분하고, 각각의 경우에 대해 굴착 폭은 심도의 1.5배로 가정하였다.
흙막이 벽체 형식은 대심도 터파기 시 주변 건물에 미치는 영향을 최소화하기 위해 강성이 큰 지하연속벽(Diaphragm wall)과 SBP(Secant Bored Pile) 벽체로 계획된 사례가 많았다. 본 연구에서는 최근에 국내 적용사례가 증가하고 있는 SBP 벽체보다는 엔지니어들에게 조금 더 친숙한 지하연속벽을 해석대상 벽체로 결정하였고, 두께는 800mm, 근입 심도는 굴착 바닥면으로부터 2m 또는 암반 2m 근입 조건으로 해석을 단순화하였다.
지보재는 앵커가 계획된 사례들도 많았지만, 도심지 조건에서 부지점용과 상관없이 적용할 수 있는 버팀보 형식 중 터파기 시공성이 좋은 강관버팀보를 해석대상 지보재로 결정하였다. 강관버팀보의 두께는 설치 위치와 상관없이 9mm를 동일하게 적용하였고, 수직 간격은 시공성을 고려하여 기본적으로 2.5m를 유지 시키되, 토압이 작은 암반층에서는 3.0∼4.0m까지 증가시켰다. 그리고 수평 간격은 띠장 설계와의 연관성을 고려하여 4.0m로 결정하였다.
지하연속벽과 강관버팀보의 단면 가정조건은 실무에서 가장 많이 적용되고 있는 Midas 탄소성해석을 통해 적정성을 확인하였으며, 이상의 과정을 통해 결정된 지층구성과 굴착규모(심도, 폭)를 해석조건에 따라 정리하면 Table 4와 같다.
3. 수치해석 모델링
흙막이 시설물의 지진시 거동 특성을 평가하기 위해 지반공학분야에서 적용성이 검증된 유한차분 해석 프로그램인 FLAC 2D Version 8.1(ITASCA Consulting Group, 2021)을 이용하여 동해석을 수행하였다. 굴착 규모와 지반 조건에 따라 결정된 네 가지 해석 Case에 대해 굴착 단계별 정적 해석을 수행하고, 굴착이 완료된 최종 단면을 대상으로 동적 해석을 진행하였다. 일반적으로 탄소성 해석에서는 지보재의 변위가 발생하지 않는 중앙부를 경계로 반단면의 대칭 해석을 수행하지만, 지진하중 작용시 흙막이 시설물과 지반의 상대적인 움직임을 고려하기 위해 전단면을 대상으로 해석을 진행하였다. 상세한 해석 조건과 과정은 다음과 같다.
3.1 수치모델 및 해석순서
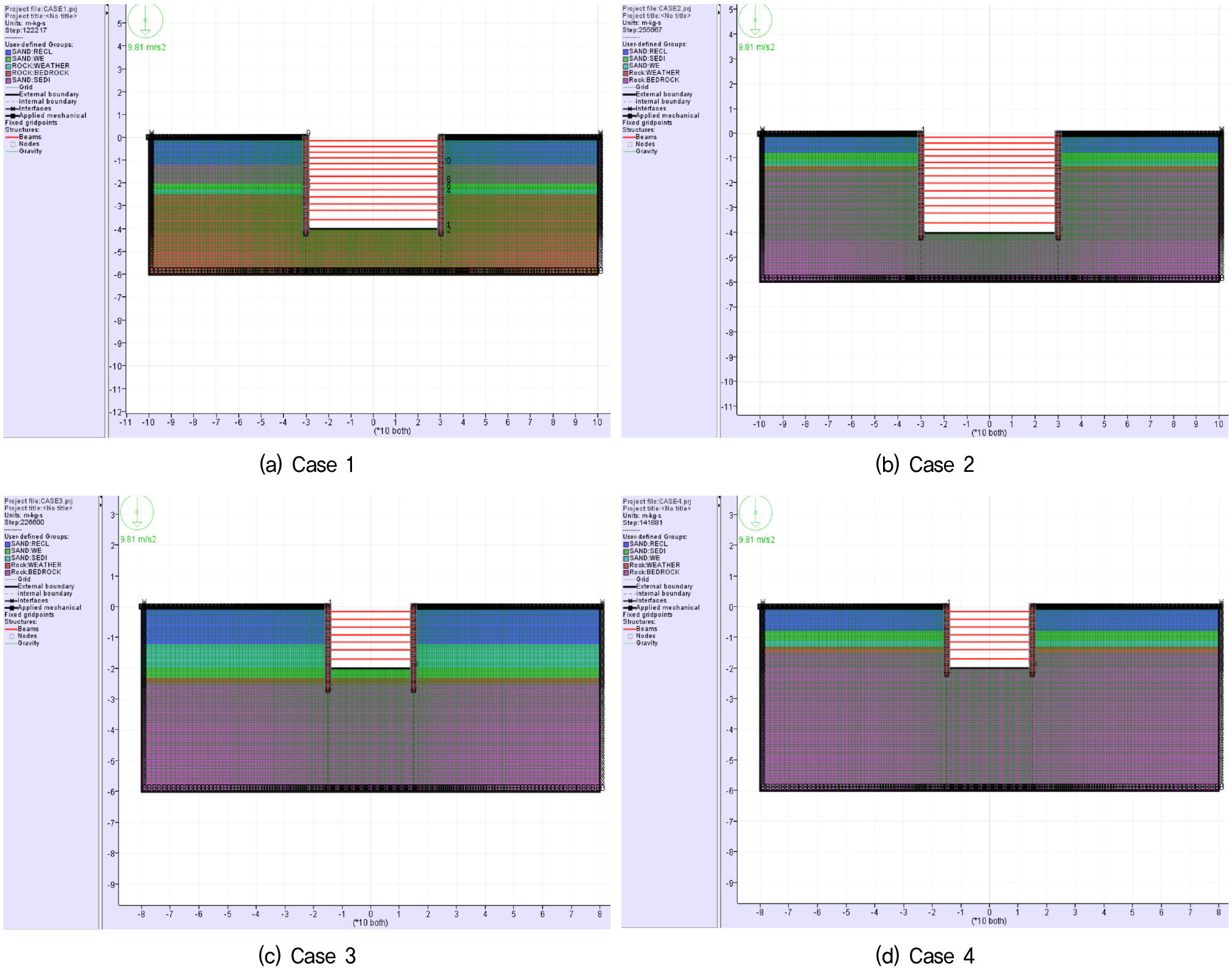
굴착 규모에 따라 굴착면의 중앙부를 기준으로 Case 1, 2는 횡방향으로 200m, Case 3, 4는 160m의 범위까지 모델링 하고, 입력지진파를 같은 심도에 작용시키기 위해 연직방향은 지표면으로부터 60m까지 동일한 깊이로 모델링 하였다. 지반은 Mohr-Coulomb 모델을 적용하고, 지하연속벽과 강관버팀보는 빔 요소(Beam element)를 적용하였다.
수치해석은 “Grid 생성 → Boundary condition 및 Interface 특성 입력 → Mesh 생성 → 지반 물성 입력 → 초기 지중응력 상태 구현 → Diaphragm wall 생성 → 지표면 상재하중(장비하중) 재하 → 단계별 굴착 및 지보재 설치 → 최종 굴착 완료 → 동적 물성 입력 → 지진 경계조건 및 지진하중 재하”의 순서대로 진행하였으며, 단계별 굴착이 완료된 최종 단면의 형상은 Fig. 1과 같다.
3.2 입력지진파
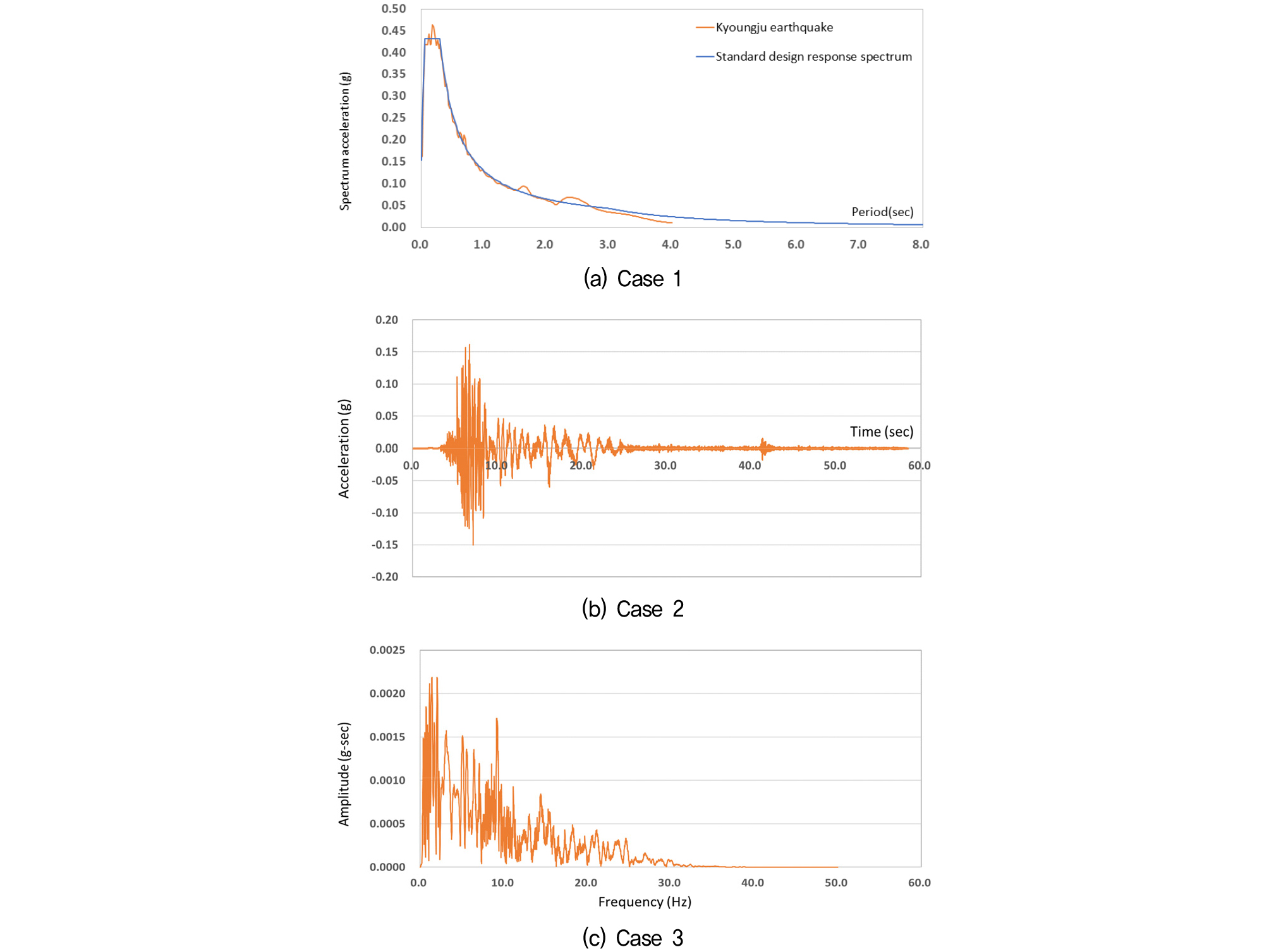
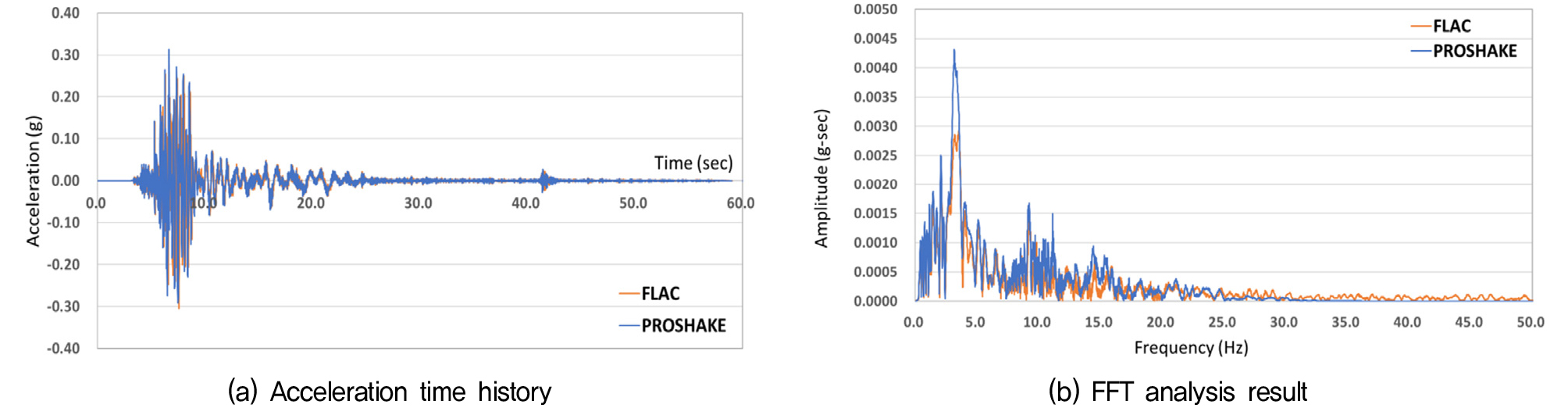
수치해석을 위한 지진파로는 2016년 경주에서 계측된 지진파를 적용하고, 가속도의 크기는 수도권 주요 토목구조물의 내진설계에 적용되고 있는 내진 1등급 붕괴방지수준에 해당하는 재현주기 1,000년의 값을(0.154g) 적용하였다. 내진설계기준(KDS 17 10 00)에 따라 Fig. 2(a)와 같이 실 계측 지진파의 응답스펙트럼을 설계응답스펙트럼에 맞게 보정하는 과정을 거쳤으며, 이 과정을 통해 결정된 입력 지진파의 가속도 시간이력과 FFT 해석 결과를 각각 Fig. 2(b)와 Fig. 2(c)에 나타냈다. Fig. 2(c)에서와 같이 경주지진파는 10Hz 이상의 고주파 성분이 비교적 높은 가속도 값을 보여, 앞서 가정된 두 가지의 지반조건 중 S3 지반에서 더 큰 가속도 증폭이 발생하고, 동적 토압이 구조물에 미치는 영향이 더 클 수도 있을 것으로 예상되었다.
3.3 지반요소
FLAC 동해석에서는 지반 모델링에 적용한 요소의 크기에 따라 전파되는 지진파의 최대 주파수 크기가 결정되므로, 요소의 크기가 부적절할 경우에는 해석 결과의 신뢰도에도 영향을 미칠 수 있다. 지반요소의 크기는 Kuhlemeyer and Lysmer(1973)의 연구결과에 따라 아래 식 (1)과 같이 지진파의 주파수 성분과 매질의 전단파 속도와의 상관관계에 따라 결정할 수 있으며, 본 해석에 적용한 경주지진파는 약 25∼30Hz까지 유의미한 에너지대역을 보이고 있고, 매립 모래의 전단파속도가 180m/s였기 때문에 지반요소의 크기는 0.6m∼0.7m 이하로 적용하는 것이 합리적인 것으로 판단되었다. 이에, 벽체와 인접한 지반요소의 크기는 0.5m를 적용하였고, 동일한 요소 크기를 전체 해석영역에 일률적으로 적용했을 경우 해석시간이 너무 길어진다는 단점을 해결하고자 모델의 경계부로 가면서 요소의 크기를 일정비율로 증가시켰다.
여기서, Δl : 메시의 최대크기
λ : 지진파의 파장
f : 지진파의 주파수
Vs : 매질의 전단파속도
3.4 지반물성
지반 모델은 Mohr-Coulomb 모델을 적용하였으며, 기본물성과 정적, 동적 해석을 위한 변형계수 값은 기존 프로젝트에서 수행된 지반조사결과와 Sun 등(2012)의 연구결과를 토대로 아래 Table 5와 같이 적용하였다.
Table 5.
Engineering properties for numerical analysis
동적해석을 위한 물성값 중 전단탄성계수(Gd) 값을 산정하는 방법에는 여러 가지 방법이 있으나, 본 연구에서는 동일한 지층에서 전단파속도(Vs)가 일정한 것으로 가정하여 아래 식 (2)에 따라 결정하였다.
여기서, ρ : 단위밀도
Vs : 전단파속도
지반의 전단탄성계수와 감쇠비는 지진하중 작용시 발생하는 전단변형율의 크기에 따라 비선형적 거동을 보이게 되는데, FLAC에서는 두 가지 방법으로 비선형 특성을 고려할 수 있다. 첫 번째 방법은 지반응답해석을 통해 각 지층에서의 유효 전단변형율을 산정한 후, 해당 변형율에서의 전단탄성계수 감소계수와 Rayleigh damping 값을 추정하여 수치해석 중 일정한 전단탄성계수와 감쇠비를 적용시키는 방법이다. 두 번째 방법은 기존 연구자들이 제시한 전단변형율에 따른 정규화 전단탄성계수 감소곡선과 Hysteretic damping 곡선을 지반물성으로 직접 입력하여, 수치해석 중 발생하는 변형율의 크기에 따라 지반물성을 자동적으로 변경시키는 방법이다. 해석의 편의성이나 정밀도, 해석시간 등 여러 가지 측면에서 각각의 장단점이 있으나, 지층조건이 여러 개의 지층으로 구성되어 있고 지진으로 인한 변형율의 변화정도가 커다란 경우에는 Rayleigh damping과 비교하여 Hysteretic damping을 적용하는 것이 보다 현실적인 결과를 도출하는 것으로 알려져 있다. FLAC 프로그램에는 Seed and Idriss(1970)의 방법을 포함하여 기존의 연구자들이 제시한 G/Gmax - strain, Damping ratio - strain 곡선을 모사할 수 있는 몇 가지의 Fitting curve가 내장되어 있는데, 본 연구에서는 Default fitting curve model을 이용하여 지반의 비선형 거동을 모사하였다. 상기의 방식을 적용함으로써 Rayleigh 감쇠와는 달리 지진파 주파수 성분의 영향을 받지 않는 Hysteretic damping을 구현할 수 있었으며, Hysteretic damping을 통해 감쇠되지 않는 고주파 성분의 노이지를 제거하기 위해 0.2% 정도의 stiffness proportional Rayleigh damping을 추가적으로 적용하여 해석의 정확도를 높였다.
3.5 구조체 모델링
흙막이 시설물의 벽체로 적용된 지하연속벽은 두께 800mm의 철근콘크리트 구조물이고, 지보재는 직경 406mm, 두께 9mm의 강관스트럿으로써, 두 구조요소 모두 빔 요소로(Beam element) 모델링 하였다. 지보재와 벽체의 연결부는 힌지로 모사하였고, 지하연속벽 구조부재와 지반요소의 경계면은 서로 다른 이질재료(콘크리트-지반) 간의 미끄러짐(Sliding)과 분리거동(Opening)이 일어날 수 있도록 경계요소(Interface element)를 적용하였다. 경계요소의 전단방향(ks), 연직방향(kn)강성은 구조요소와 인접한 지반 중 강성이 가장 큰 지반을 대상으로 아래 식에 따라 산정할 수 있다.
여기서, K : 체적탄성계수
G : 전단탄성계수
Δzmin : 구조요소와 인접한 지반의 최소 폭
3.6 내진해석 모델의 경계조건
FLAC 동적해석을 위한 하부경계조건은 Rigid base로 모사하는 방법과 Compliant base로 모사하는 두 가지 방법이 있다. Rigid base는 모델 하부경계를 고정하고 가속도 시간이력을 하부경계에 직접 적용하는 방법으로, 모사하고자 하는 가속도를 그대로 입력할 수 있어 편리하다는 장점이 있다. 그러나 암반 노두에서 계측된 Outcrop motion을 직접 입력할 경우 실제 기반암 가속도보다 더 큰 가속도가 입력될 수 있고, 이를 극복하기 위해서는 별도의 1차원 지반응답해석을 통한 Deconvolution 과정을 통해 지진파를 입력해야 하는 단점이 있다. 또한 토층에서 반사되어 하향으로 전파된 가속도가 다시 해석영역 내부로 반사되어 무한 Trap이 발생할 수 있다는 단점이 있어(Park et al., 2010), FLAC 매뉴얼에서도 이에 대한 주의를 요구하고 있다. 이에 반해 Compliant base는 아래 식 (4)와 같은 변환과정을 통해 산출한 전단응력 시간이력을 입력 지진파로 입력하고 하부경계에는 Lysmer et al.(1972)이 개발한 점성댐퍼를 적용하는 방법으로써, 가속도 변환과정이 필요하다는 번거로움이 있으나 상부층에서 반사되어 하부로 전달되는 진동을 흡수시켜 지반진동의 과대예측을 방지하고, 별도의 Deconvolution 과정이 필요 없다는 장점이 있다(Joyner et al., 1975; Kwok et al., 2007).
FLAC 매뉴얼과 기존의 연구결과에 따르면 2차원 동적해석을 위해 Compliant base를 적용하는 것이 가장 신뢰성이 높은 것으로 알려졌으며, 이에 본 연구에서도 경주 지진파의 가속도 시간이력을 적분하여 속도 시간이력을 산정한 후, 이를 식 (4)에 따라 응력 시간이력으로 변환시키고, Compliant base를 적용하여 동적 해석을 수행하였다. 측면 경계조건은 지진파의 소산을 모사하기 위하여 무한요소인 자유장 경계조건을 적용하였다.
여기서, vs : Outcrop motion의 속도 시간이력
Cs : 기반암의 전단파 속도
ρ : 기반암의 밀도
4. FLAC 해석 모델링의 적정성 검증
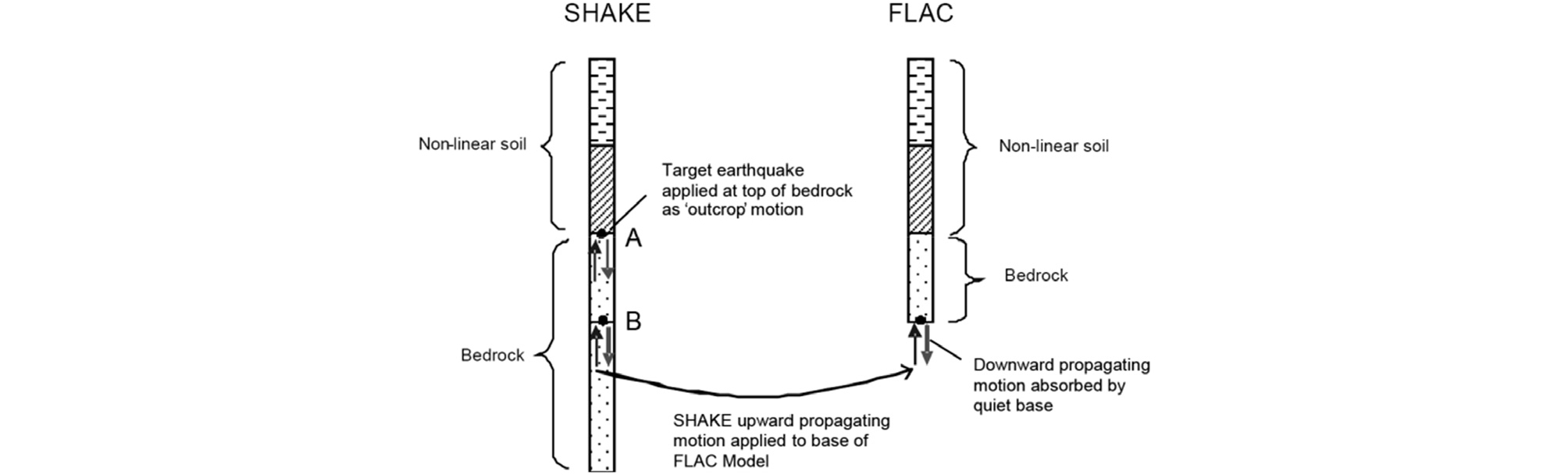
본 해석에 앞서 흙막이 시설물이 설치되기 이전 원지반을 대상으로 2차원 지반응답해석을 수행하고, 이 결과를 실무에서 가장 많이 사용되고 있는 1차원 지반응답해석(Pro-Shake ver. 2.0) 결과와 비교하여, 본 연구에서 적용한 동적 해석 모델의 경계조건, 지반 요소의 크기, 그리고 동적 물성의 적정성을 확인하였다. 1차원 해석은 매질의 층별 두께를 1m로 조정한 것을 제외하면 2차원 해석과 모두 동등한 입력 지반물성에 대해 해석이 이루어졌다. 1차원, 2차원 지반응답해석의 가장 커다란 차이점은 지진하중을 적용시키는 방법인데, Fig. 3의 개념도(Mejia, L. H., and E. M. Dawson, 2006)와 같이 동일한 에너지의 하중조건에서 지반응답해석이 이루어질 수 있도록, 2차원 해석에서는 앞서 기술한 Compliant base에 전단응력의 시간이력 함수를 적용시켰고, 1차원 해석에서는 기반암 상부 위치에 가속도 시간이력을 Outcrop Motion으로 재하시켰다.
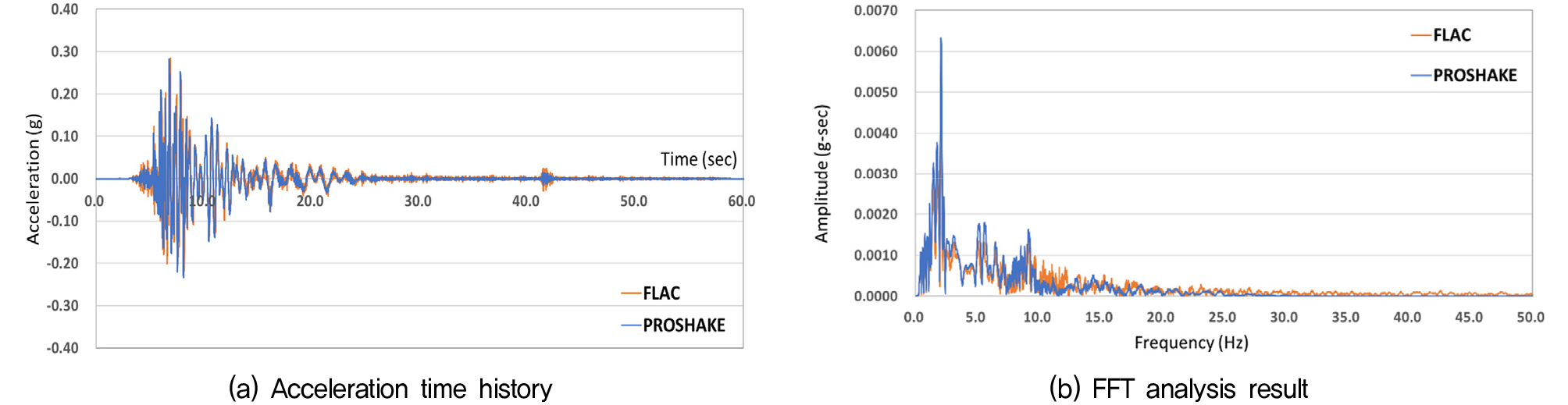
1차원, 2차원 수치해석을 통해 지표면에서 산정된 가속도 시간이력과 FFT 해석 결과를 각각 Fig. 4, Fig. 5에 도시하고, 최대 가속도 값을 Table 6에 정리하였다. 1차원, 2차원 해석 모두 기반암의 출현 심도가 얕은 경우에 지표면 가속도가 더 크게 산정되었고, 이는 단주기 성분이 우세한 지진파의 특성 상 고유주기가 0.246초로 작은 S3 지반에서 고유주기가 0.414초로 길었던 S4지반에 비해 더 커다란 증폭이 발생했기 때문으로 판단된다. FLAC과 Pro-Shake는 해석 기법의 차이에도 불구하고 가속도 시간이력과 FFT 해석 결과가 전반적으로 매우 유사한 것으로 나타났으며, 특히 지표면 최대 가속도 값이 약 5% 내의 미소한 차이를 보여, FLAC 해석 모델의 경계조건, 지진파의 주파수 성분을 고려한 지반요소의 크기, 동적 물성은 모두 적절하게 모델링 된 것으로 판단된다.
5. 수치해석 결과
지반을 단계별로 굴착하는 과정에서 지진이 발생할 확률은 낮고, 굴착심도가 클수록 지진하중이 벽체에 미치는 영향이 클 것으로 판단되므로, 본 연구에서는 Table 4에 기술한 네 가지 해석 Case에 대해 Table 7과 같이 단계별 굴착을 모사한 후, 굴착이 완료된 최종 단면을 대상으로 내진해석을 수행했다.
Table 7.
Step by step excavation and dynamic analysis procedure
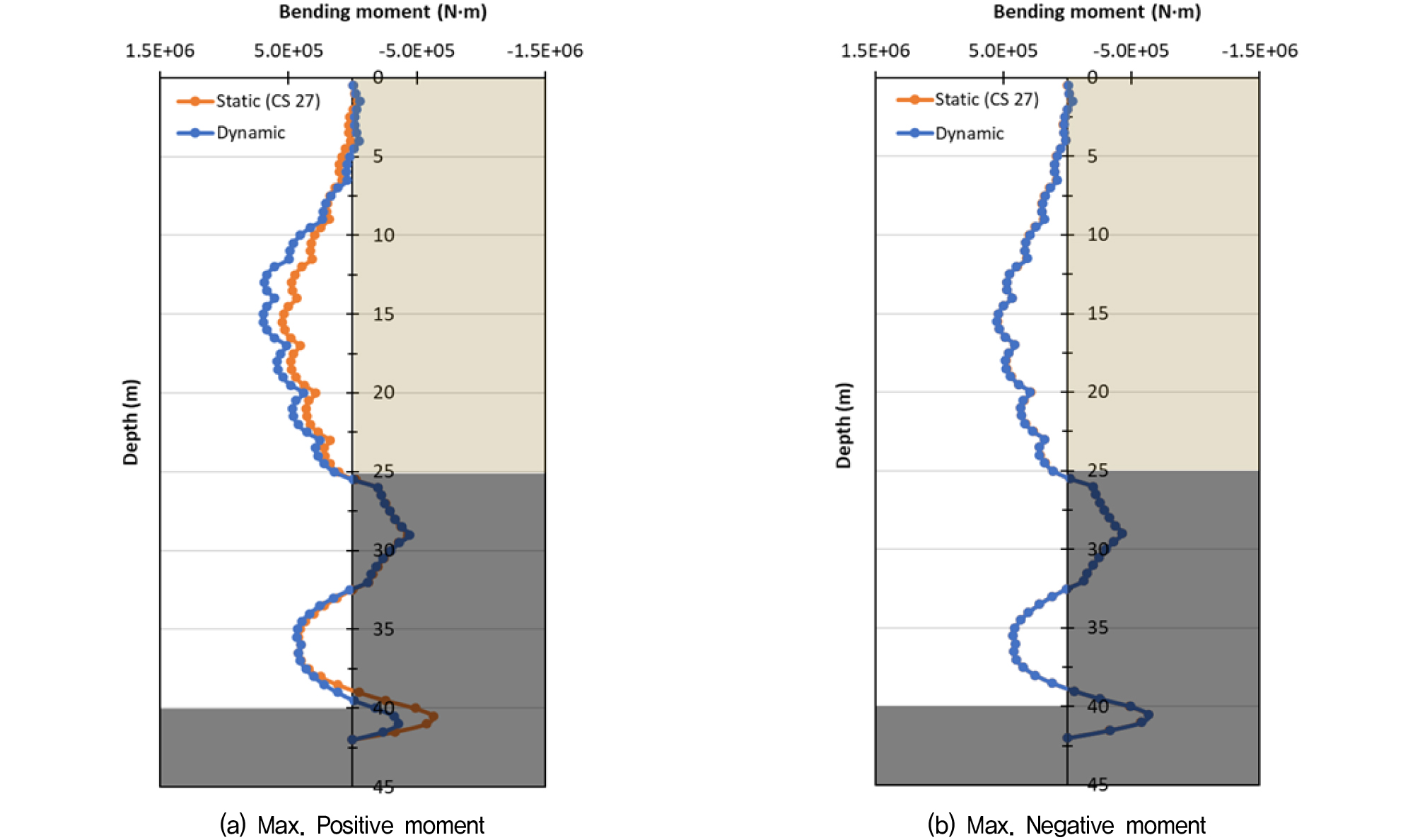
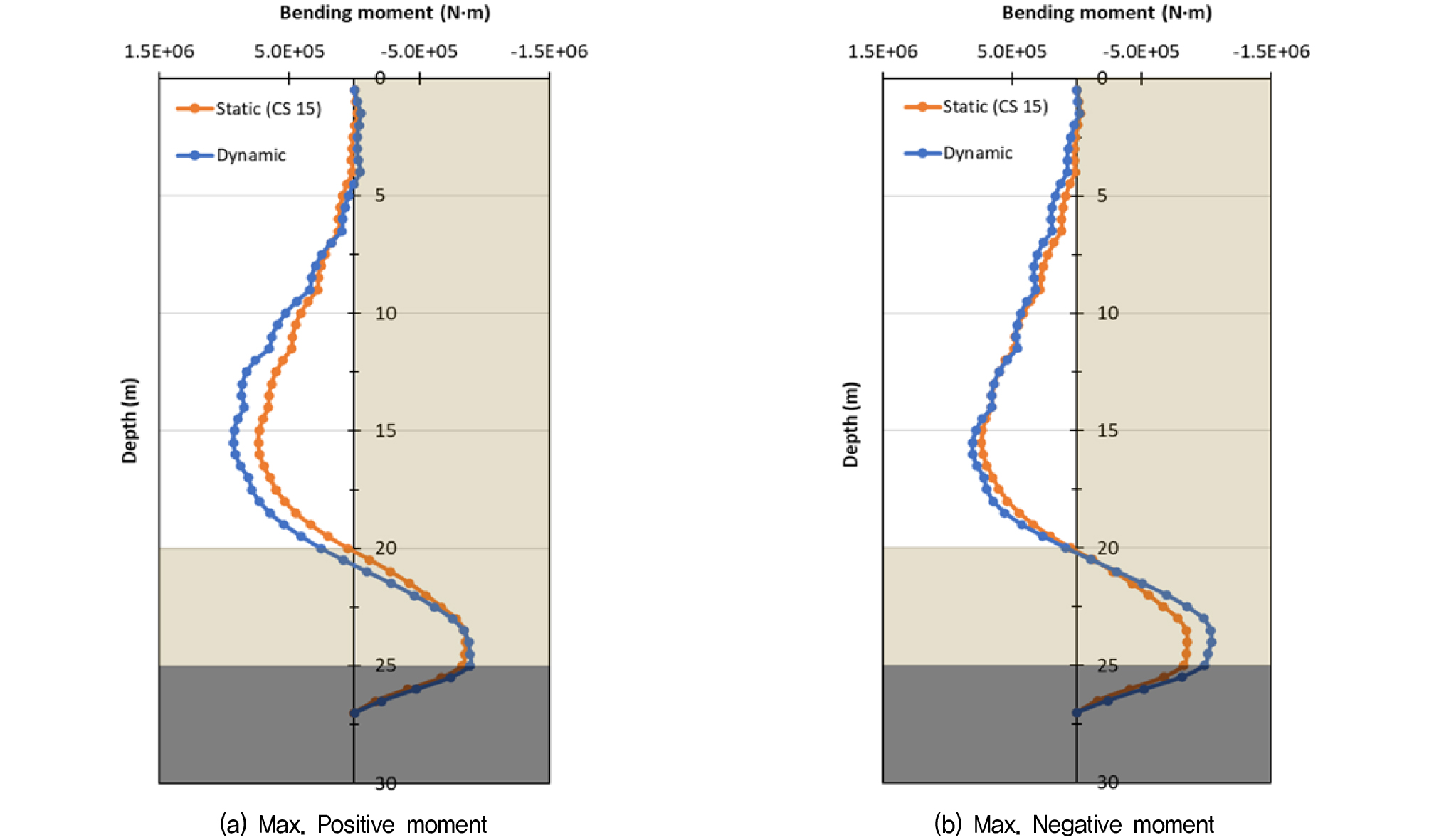
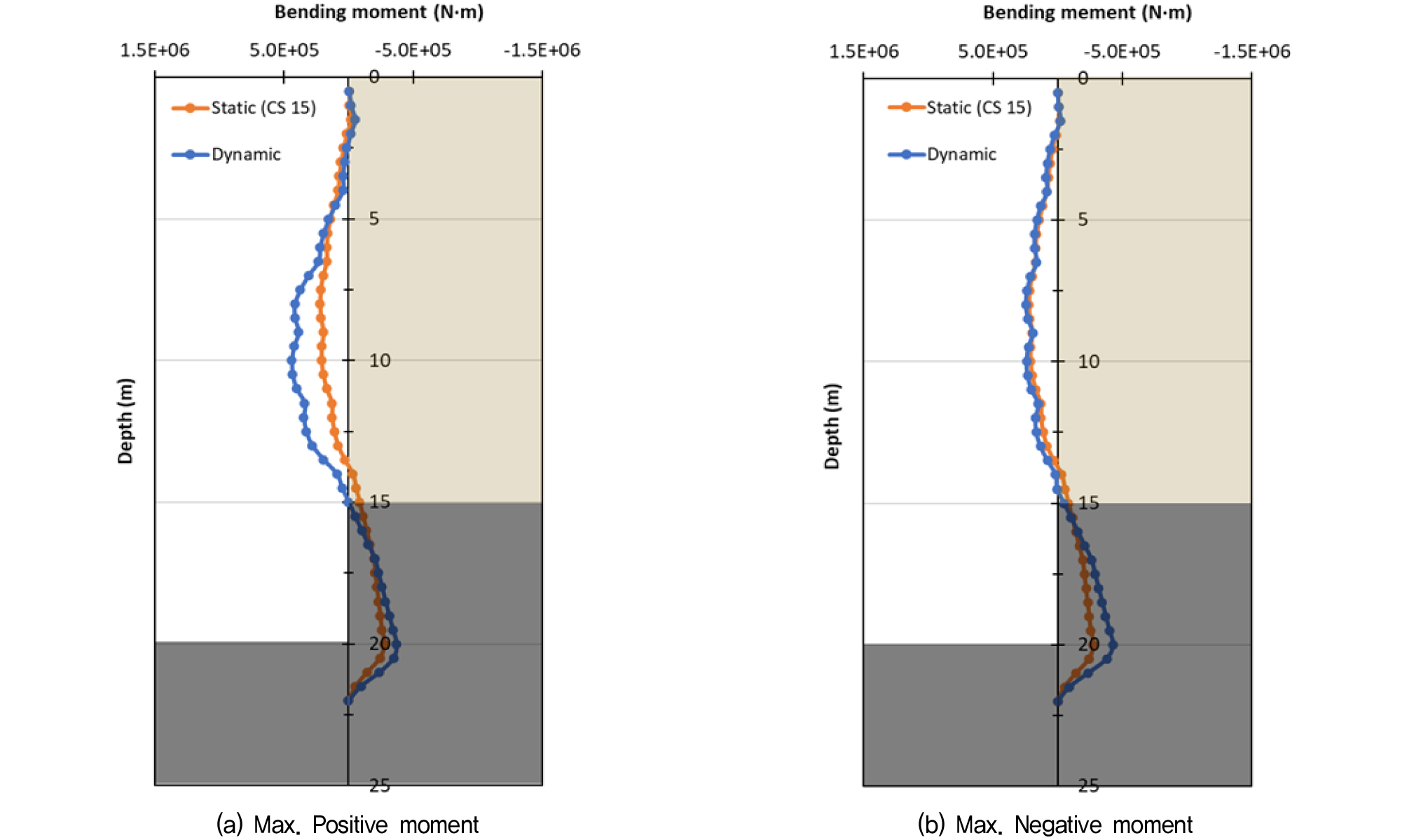
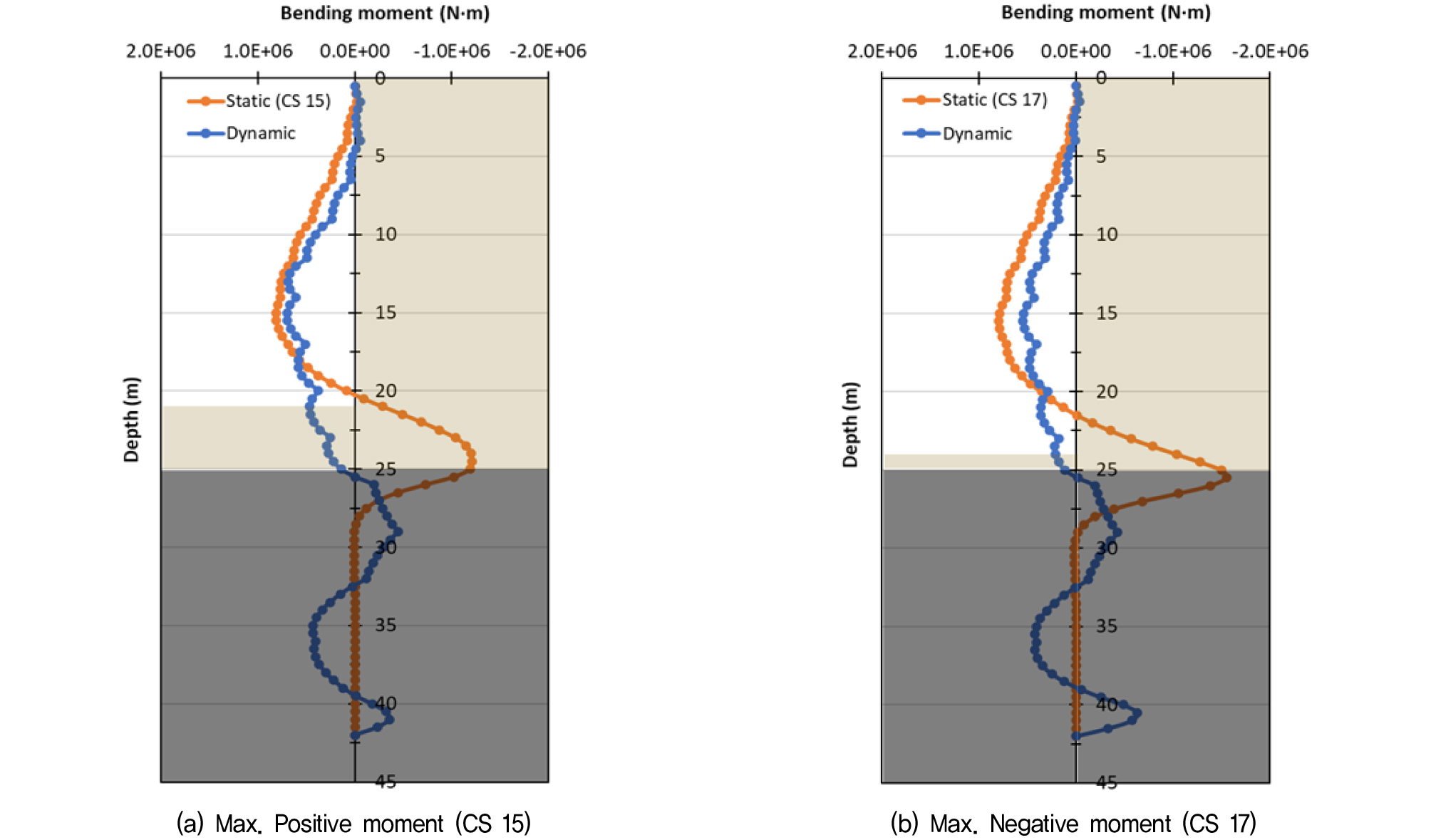
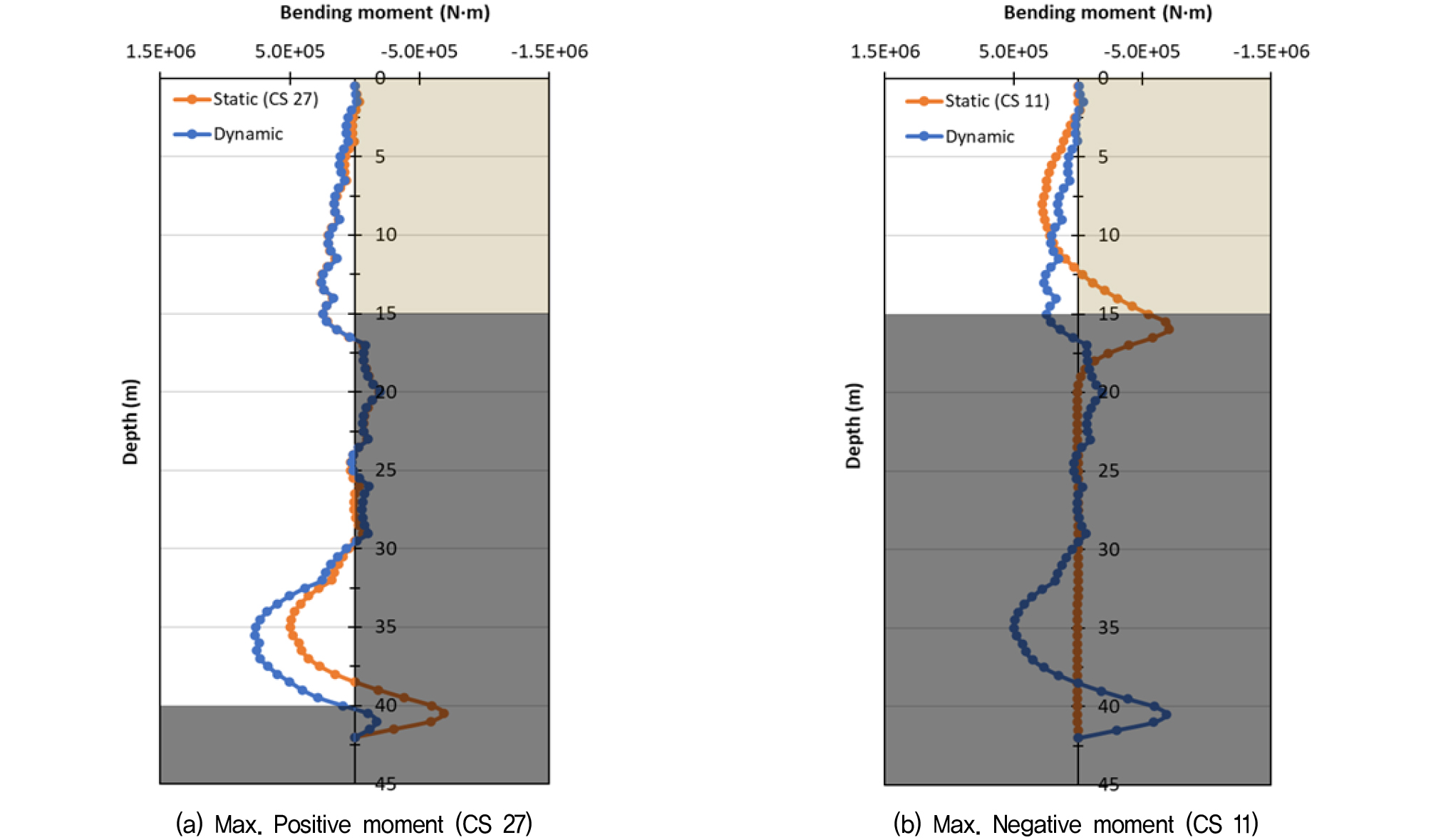
우선 지진하중 작용 시 벽체의 최대 정모멘트와 부모멘트가 발생했을 시점을 기준으로 깊이별 모멘트도를 작성한 후, 이를 지진 하중 작용 전 최종 굴착단계에서의 모멘트도와 비교하여 Fig. 6∼9에 도시하고, 최대 값을 Table 8에 정리하였다. 기반암의 출현심도보다 굴착 심도가 매우 깊었던 Case 1, 2의 경우, 최종 굴착단계와 비교하여 지진하중 작용 시 최대 정모멘트는 약 27∼50%정도 증가하였고, 최대 부모멘트는 거의 변화가 없는 것으로 나타났다. 굴착 심도가 기반암 출현심도 대비 얕거나 비슷했던 Case 3, 4의 경우 정모멘트는 약 26∼98%정도 증가하였고, 부모멘트도 Case 1, 2와는 다르게 약 21%∼54%까지 증가하는 것으로 나타났다. 이상의 결과를 통해, 지진하중으로 인한 동적 토압의 영향으로 굴착방향으로의 정모멘트는 전반적으로 증가하려는 경향을 보이며, 배면측으로의 부모멘트는 기반암 출현 심도와 굴착 심도의 상대적인 관계에 따라 토압의 영향 정도가 달라지는 것으로 판단된다. 한편, 기반암 출현 심도가 15m로 얕은 Case 2와 Case 4의 경우에는 최대 정모멘트가 지진하중 작용 전과 비교하여 각각 50%, 98%까지 증가하여, 기반암 출현 심도가 25m로 깊었던 Case 1과 Case 3과 비교하여(26%∼27%) 지진하중이 벽체에 미치는 영향이 더 큰 것으로 나타났는데, 이는 앞서 예측했던 바와 같이 단주기 성분이 우세한 경주 지진파의 특성 상 기반암 심도가 얕은 S3 지반에서 지반 증폭이 더 크게 발생하여 동적 토압의 영향이 더 커졌기 때문으로 판단된다.
Table 8.
Comparison of maximum bending moment (Final Exca. Static vs Dynamic)
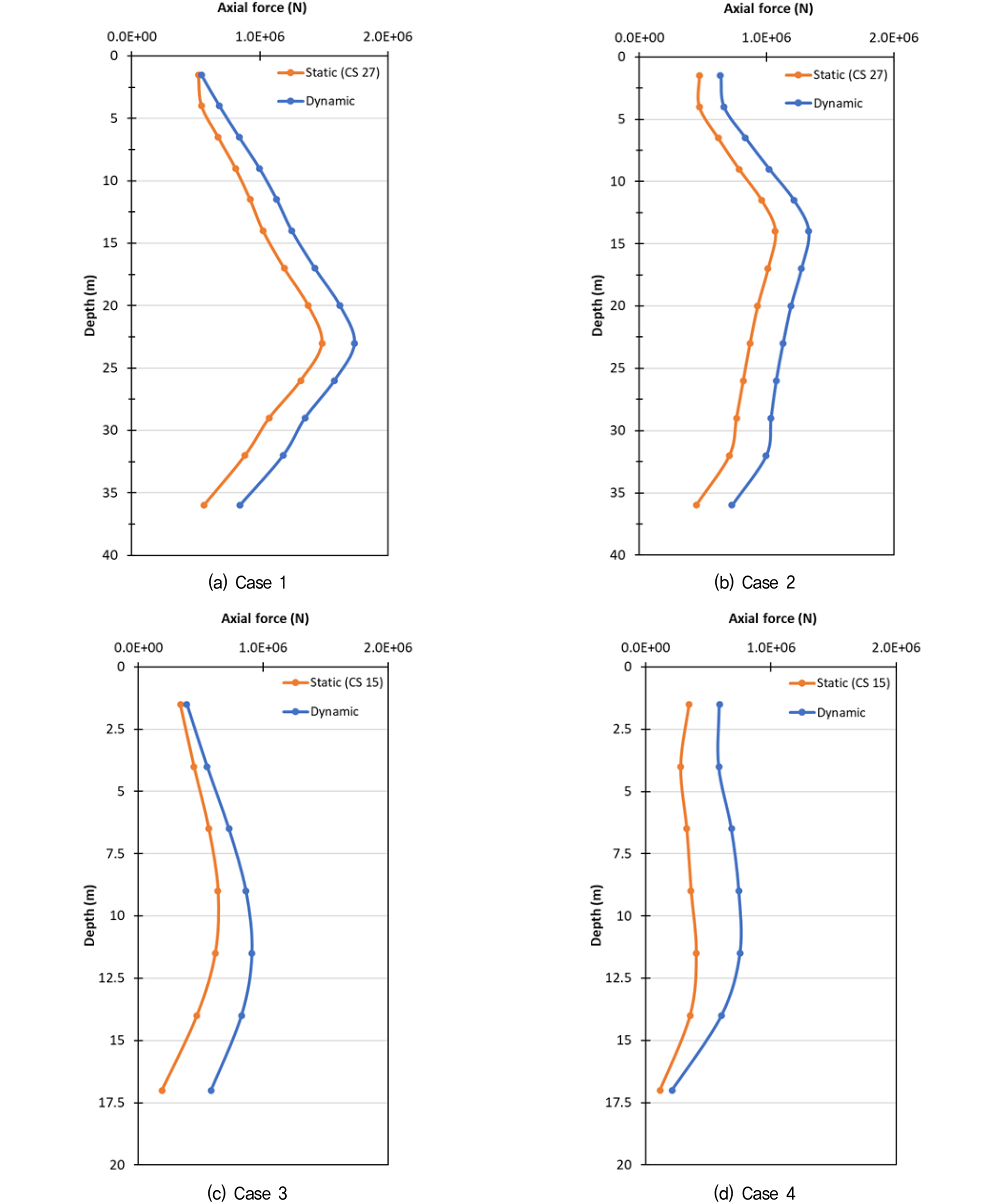
다음으로 지진하중 작용 시 지보재에 발생한 최대 축력을 지진하중 작용 전 최종 굴착단계에서의 축력 값과 비교하여 Fig. 10에 도시하고, 축력이 가장 크게 발생한 지보재를 대상으로 축력의 최대값을 Table 9에 정리하였다. 해석 조건에 따라 차이가 있으나 지진하중 작용 시 최대 축력이 17∼87%까지 증가하여, Soil Nailing을 대상으로 수치해석을 수행한 Khaja Moniuddin et al.(2016)의 연구결과와 유사하게 지진으로 인한 동적 토압이 지보재에 미치는 영향이 매우 큰 것으로 나타났다. 특히 앞서 벽체 모멘트 분석 결과와 마찬가지로 기반암 출현 심도가 얕은 S3 지반조건에서(Case 2, 4) 기반암 심도가 깊은 S4 지반조건과 비교하여(Case 1, 3) 축력의 증가 정도가 더 큰 것으로 분석되었다.
6. 지진하중이 흙막이 구조물의 설계에 미치는 영향
동적 해석 결과와 같이 조건에 따라 정도의 차이를 보이지만 지진하중은 흙막이 시스템의 부재력에 영향을 미치고, 따라서 현행 기준에 따라 정적인 하중 조건에서 설계된 흙막이 벽체와 지보재의 안정성에도 영향을 미칠 수 있을 것으로 예상된다. 이에 단계별 굴착 해석 결과로부터 도출한 벽체의 모멘트와 지보재의 축력을 이용하여 현행 흙막이 설계기준에 따라 정적 설계를 수행한 후, 동해석으로부터 산출한 지진하중 조건에서의 벽체 모멘트와 지보재의 축력이 정적인 하중 조건에서 설계된 부재의 안정에 미치는 영향을 평가하였다. 흙막이 설계는 가설흙막이 설계기준(KDS 21 30 00: 2020)을 기준으로 하되, 강관버팀보에 대한 내용은 도로교설계기준(국토해양부, 2010)을 따르고, 띠장 설계는 구조물기초설계기준(KGS, 2018)을 적용하였다. 가시설 흙막이는 영구구조물로 사용되는 경우와 임시구조물의 공사기간에 따라 가설 할증계수를 달리 적용하는데, 대규모·대심도 흙막이의 경우 지하구조물 설치 후 해체시까지 공사시간 2년 이상을 가정하여 가설 할증계수로 1.25를 적용하였다. 그리고 흙막이 공사시 신강재를 사용하더라도 재사용 또는 부식 등의 가능성을 대비하여 강재응력 감소계수 0.9를 적용하였다.
6.1 지진하중이 벽체 설계에 미치는 영향
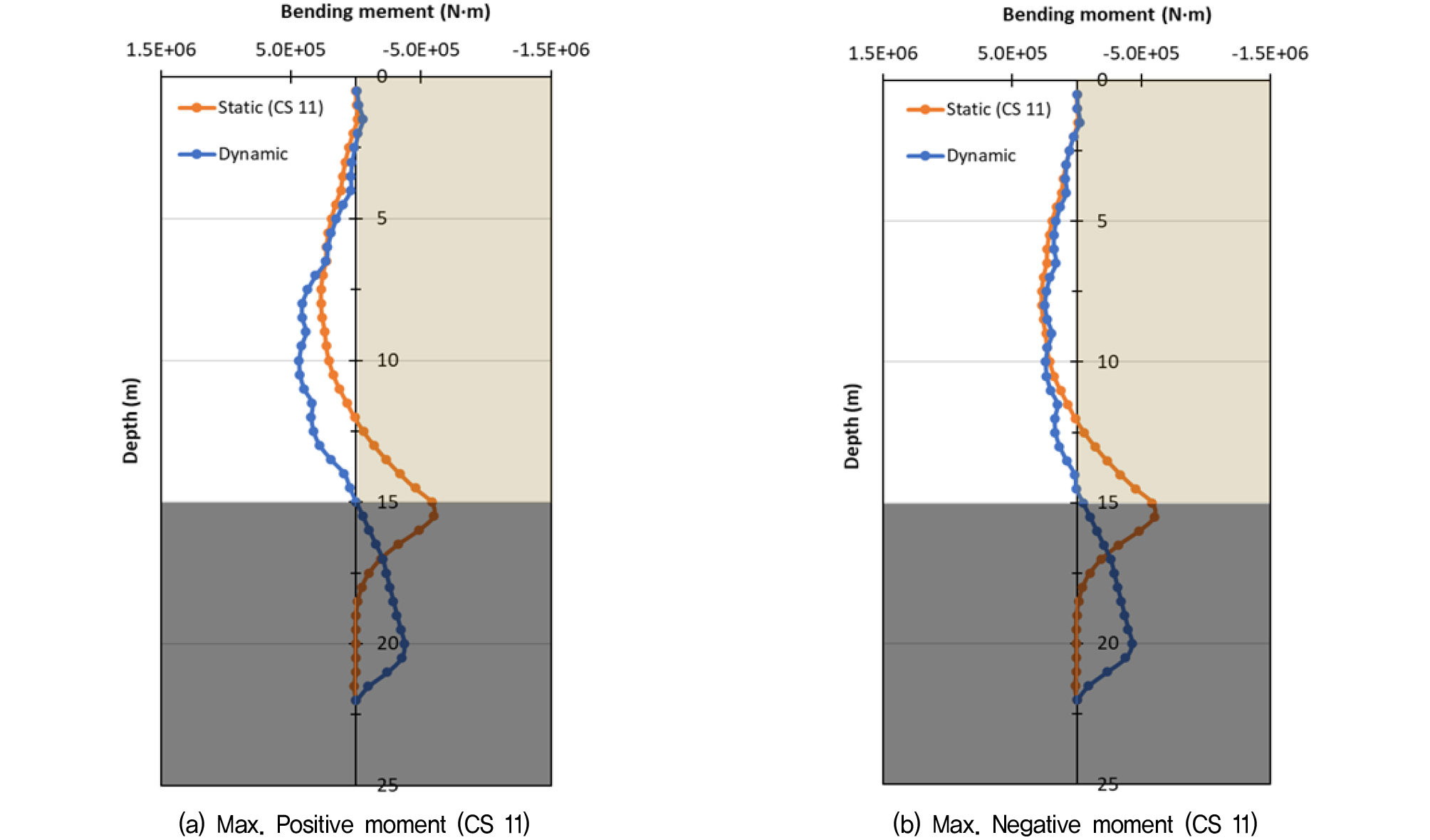
지하연속벽의 안정성(제원)은 굴착 중 벽체에 발생하는 최대 모멘트의 크기에 따라 결정된다. 그런데 상시조건에서 벽체 설계를 위해 적용하는 최대 모멘트는 최종 굴착 단계에서 발생할 수도 있지만, 단계별 굴착 과정 중에도 발생할 수도 있다. 본 연구에서는 토사층에서 굴착이 종료된 Case 3의 경우 최종 굴착 단계에서 최대 모멘트가 발생하였고, 나머지 Case 1, 2, 4의 경우 최종 굴착단계에 도달하기 전 단계별 굴착 과정 중에 최대 모멘트가 발생하는 것으로 나타났다. 이에 Fig. 6∼9에 나타냈던 최종 굴착 단계에서의 모멘트와는 별도로, Case 1, 2, 4의 경우에 대해 굴착 과정 중에 발생한 최대 모멘트를 지진시와 비교하여 Fig. 11∼13에 도시하였다. 그리고 상시·지진 시 조건에서 벽체 설계에 적용할 최대 모멘트 값을 Table 10에 비교하였다. 상시조건에서 최대 모멘트는 모두 부모멘트 방향에서 발생하였고, 토사층에서 굴착이 종료된 Case 3을 제외하고 모두 토사층과 기반암층의 경계부에서 최대 값이 나타났다. Case 1과 Case 4의 경우, 굴착 중에 발생한 최대 모멘트가 지진하중 작용 시에 발생한 최대 모멘트보다 큰 것으로 나타나, 지진하중이 벽체의 단면설계에는 영향을 미치지 않을 것으로 보인다. 그러나 Case 2와 Case 3의 경우에는 지진시의 모멘트가 상시 대비 약 10%∼21% 정도 크게 나타나, 지진시 조건에 대한 별도의 구조 해석이 필요할 것으로 판단된다.
Table 10.
Comparison of maximum bending moment for design (Static & Dynamic)
Case 2와 Case 3을 대상으로, 앞서 언급한 현행 흙막이 설계기준에 따라 상시 최대 모멘트를 이용하여 단면설계를 수행한 후, 지진으로 발생한 모멘트가 벽체의 안정성에 미치는 영향을 평가하였다. Table 11과 같이 상시조건에 발생한 응력이 허용응력 대비 86% 수준이 되도록 철근을 배근하고, 지진 시 발생한 최대 모멘트로 추가의 구조해석을 수행한 결과, Case 2에서는 소요철근량이 사용철근량의 94%까지 증가하였으나 안전상에는 문제가 없었으며, Case 3의 경우에는 소요철근량이 사용철근량보다 더 큰 것으로 나타나 철근배근을 증가시킬 필요가 있는 것으로 나타났다. 그러나 본 연구에서는 철근량을 계산하는데 있어 지진시 조건에서 별도로 적용할 수 있는 허용응력 증가계수 값이 없었던 관계로, 상시 조건과 동일한 값인 1.25를 적용했으므로, 향후 지진시 조건에서 합리적인 구조해석이 이루어지기 위해서는 적정한 보정계수가 정립되어야 할 것으로 판단된다.
Table 11.
Structural design of diaphragm wall
6.2 지진하중이 지보재 설계에 미치는 영향
지보재는 굴착 단계 중 발생하는 최대 축력과 중간말뚝의 간격에 따라 결정되는 휨모멘트나 전단력에 대한 구조적 안정성을 확보해야 한다. 앞서 Table 9와 같이 지진하중 작용 시 지보재에 발생하는 최대 축력은 상시와 비교하여 약 17%∼87%까지 증가하는 것으로 나타났으며, 상시 및 지진 시 조건에 대한 지보재의 구조해석 결과는 Table 12와 같다.
Table 12.
Structural design of support system
굴착 깊이가 깊은 Case 1과 Case 2의 경우 강관지보재의 강종은 STKT 590, 중간말뚝의 간격은 7.5m를 적용하였고, 굴착 깊이가 얕은 Case 3과 Case 4의 경우에는 강종은 STK 490, 중간말뚝의 간격은 10.0m를 적용하여 상시조건에서 발생한 지보재의 부재력이 허용응력 대비 70%∼90% 수준이 되도록 설계하였다. 지진시에 발생한 최대 축력을 이용하여 상시조건에서 결정된 지보재의 재원에 대해 구조해석을 수행한 결과, 상시조건에서 여유가 많지 않았던 Case 3은 지보재에 발생한 응력이 허용응력을 초과하여 구조적으로 불안정해지는 것으로 나타났으며, 상대적으로 안전율에 여유가 많았던 Case 4의 경우에도 지진하중으로 최대 축력이 87%까지 증가하였기 때문에 불안정한 상태가 발생하는 것으로 나타났다. 또한 Case 1의 경우에도 안전율이 99.9%까지 증가하여 위험요소가 발생할 수 있는 것으로 예상되었다. 이상의 결과로 볼 때 상시조건에서 설계된 지보재가 지진시 조건에서도 구조적인 안정성을 확보하기 위해서는 지보재의 설치 간격이나 재원에 대한 재검토가 필요할 것으로 판단된다. 다만, 본 연구에서는 앞서 벽체설계와 마찬가지로 상시·지진시 조건에서 동일한 허용응력 증가계수를 적용하였으며, 합리적인 구조해석이 이루어지기 위해서는 적정한 보정계수가 확립되어야 할 것이다.
6.3 지진하중이 띠장 설계에 미치는 영향
띠장은 지보재의 최대 축력을 이용하여 연속보 조건으로 설계가 이루어지며, 구조적으로 휨응력과 전단응력에 대한 안정성을 확보해야 한다. 아래 Table 13은 상시와 지진시 조건에 대한 띠장의 구조 해석 결과이다.
Table 13.
Structural design of wale
굴착심도에 따라 띠장의 규격을 다르게 적용하였는데, Case 1과 Case 2의 경우에는 H-400x400x13x21(SM490) 규격을 적용하고, Case 3과 Case 4에서는 H-344x348x10x16(SS400) 규격을 적용하여 상시조건에 대한 비슷한 허용응력 기준으로 설정하였다. 동일한 보정계수를 적용하여 지진시 조건에 대한 구조해석을 진행한 결과, 지보재와 마찬가지로 Case 1, 3, 4에서 띠장에 발생한 휨응력이 허용응력을 초과하여 구조적으로 불안정해지는 것으로 나타나, 지진시 조건에서 안정성을 확보하기 위해서는 띠장의 재원에 대한 재검토가 필요한 것으로 나타났다. 그러나 본 검토 역시 상시조건과 동일한 허용응력 증가계수를 적용했다는 한계가 있다.
7. 결 론
본 연구에서는 유한차분해석 프로그램인 FLAC을 이용하여 가상의 대심도 흙막이 구조물을 대상으로 단계별 굴착 해석을 진행하고, 굴착이 완료된 최종 단면을 대상으로 내진해석을 수행하였으며, 다음과 같은 결론을 도출하였다.
(1) 지진시 벽체에 발생한 최대 모멘트를 지진하중 작용 전 최종 굴착단계의 모멘트와 비교한 결과, 굴착측으로의 정모멘트는 약 26∼98% 정도 증가했고, 배면측으로의 부모멘트는 굴착심도가 기반암의 출현심도 보다 매우 깊은 경우에는 변화가 거의 없었던 반면, 비슷하거나 얕은 경우에는 정모멘트와 마찬가지로 약 21%∼54%까지 증가하는 것으로 나타났다.
(2) 지진시 지보재에 발생한 최대 축력은 해석 조건에 따라 차이가 있으나 상시 대비 약 17∼87%까지 증가하여, 동적 토압이 지보재에 미치는 영향이 매우 큰 것으로 나타났다. 특히 본 연구에서 적용한 경주 지진파의 경우 단주기 성분이 우세하여, S3 지반이 S4 지반보다 축력의 증가 정도가 더 큰 것으로 나타나, 입력 지진파의 주파수 성분과 지반 고유주기의 상대적인 관계가 흙막이 시스템의 거동 특성에 커다란 영향을 미치는 것으로 분석되었다.
(3) 지진하중 작용 시 벽체에 발생한 최대 모멘트와 지보재의 최대 축력을 이용하여 상시조건에서 설계된 흙막이 시설물의 부재 안정성을 재평가함으로써, 지진하중이 현행 기준에 따라 설계된 흙막이 시설물의 안정성에 미치는 영향을 분석하였다. 그 결과 토사층에서 굴착이 종료된 경우, 지진시 벽체에 발생한 단면력이 허용응력을 초과하여 철근량의 조정이 필요한 것으로 나타났다. 그리고 대부분의 해석 조건에서 지진시 지보재와 띠장에 발생한 단면력의 최대값이 상시조건에서의 허용응력을 초과하여, 구조적인 안정성을 확보하기 위해서는 재원에 대한 재검토가 필요한 것으로 분석되었다. 그러나 현행 설계기준에서는 지진시 조건에서 적용할 수 있는 허용응력 증가계수가 제시되어 있지 않기 때문에, 본 연구에서는 구조해석시 상시·지진시 조건에서 동일한 계수 값을 적용했다는 한계가 있으며, 향후 합리적인 해석이 이루어지기 위해서는 지진시 조건에 대한 적정한 보정계수가 정립되어야 할 것으로 판단된다.
(4) 본 연구는 흙막이 구조물의 동적 거동 특성을 살펴보기 위한 기초 연구로서, 여러 가지 제한적인 조건에서 해석이 수행되었다. 향후 다양한 변수 연구를 통해 지진하중이 흙막이 구조물에 미치는 영향을 재평가할 필요가 있으며, 특히 포화지반에서 지진시 발생하는 간극 수압의 영향이 별도로 고려되어야 할 것으로 판단된다.