1. 서 론
연약지반에서 터널 굴착 시 막장 안정 확보를 위한 쉴드공법이 19세기 초 고안된 이후, 현재와 같이 막장이 격벽으로 차단되어 막장압을 유지하는 형태로 쉴드TBM의 제작기술이 발달하여 왔다. 그러나, 현재의 진보된 쉴드TBM으로도 연약지반 상 터널 굴착 시 지표침하를 완벽히 억제할 수는 없다. 그러므로, 쉴드TBM 굴착에 의한 침하형상과 크기의 예측을 통해 인접한 지상 및 지하 구조물에 대한 영향을 평가하고 대책을 수립하는 것은 여전히 중요한 이슈이다.
지표 침하형상(surface settlement trough)은 실측 침하data로부터 식 (1)과 같이 Gaussian distribution에 의해 효과적으로 나타내 질 수 있다는 Peck(1969)의 연구이후, 현장 및 실내실험의 계측자료와 수치해석을 통해 쉴드TBM 굴착에 따른 침하형상에 대한 연구가 폭 넓게 수행되고 있다(Chou and Bobet, 2002; Liao et al., 2009; Mair, 1979; McCabe et al., 2012; O’reilly and New, 1982; Rankin, 1988; Wang et al., 2016; Xu et al., 2011).
여기서, δ는 터널 중심으로부터 거리 x에서의 지표침하량, δmax는 최대지표침하량, i는 형상 폭 계수로써 터널 중심에서 변곡점까지의 거리를 나타낸다. 식 (1)에 의해 지표 침하형상을 나타내기 위해서는 변곡점까지 거리 i에 대한 추정이 필요하다. i의 제안식은 다양한 연구에서 터널 중심까지의 심도 Z0와의 선형적 관계식으로 제시되고 있으며(Arioglu, 1992; Herzog, 1985; O’reilly and New, 1982), i는 실용적으로 경험적 계수 K를 사용하여 식 (2)와 같이 산정될 수 있다(Mair et al., 1993; O’reilly and New, 1982; Rankin, 1988).
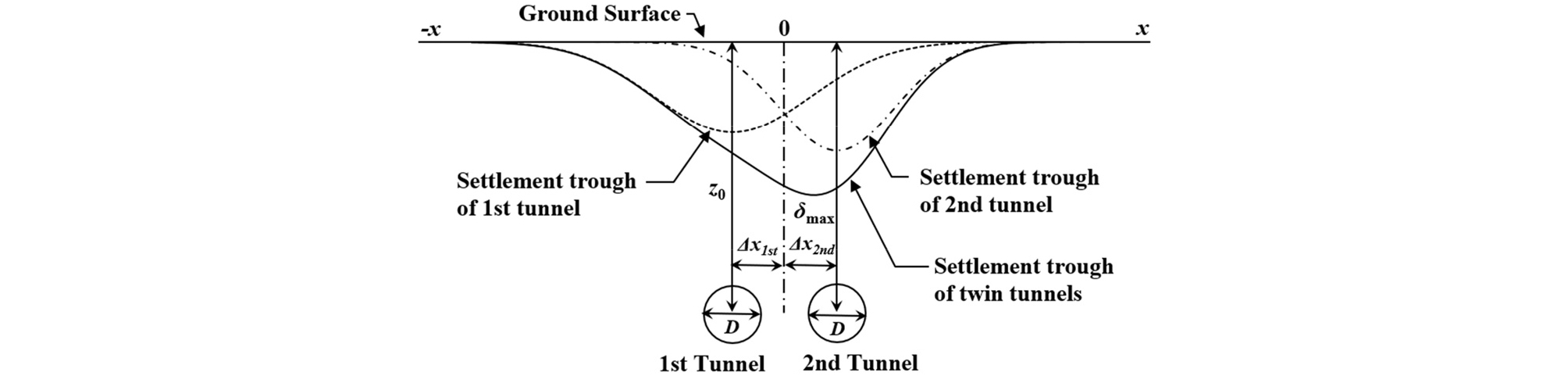
최근에는 도심지 교통해소를 위한 수단으로 터널구조물이 날로 증가되고 있다(Kim and Lee, 2003). 기존 터널구조물과 인접하여 건설되는 터널 및 병설쉴드터널이 증가함에 따라 병설쉴드터널에서의 침하형상에 대한 관측 및 침하형상에 대한 원인분석에 대한 다양한 연구보고가 수행되고 있다(Chen et al., 2018; Fargnoli et al., 2015; Jin et al., 2018; Kim, 2003; Li and Yuan, 2012; Suwansawat and Einstein, 2007; Xu et al., 2011). 특히, Suwansawat와 Einstein(2007)은 Gaussian function의 중첩원리를 이용하여 병설쉴드터널의 지표침하형상을 표현하는 방법을 현장계측자료와의 비교를 통해 제시하였다. Greenfield condition(미개발 부지 조건)에서 Gaussian function의 중첩원리를 이용한 지표침하는 아래와 같이 나타낼 수 있다(Fig. 1, 식 (3)).
여기서, 1st, 2nd는 병설터널의 선행(1st tunnel) 및 후행터널(2nd tunnel)을 나타내며, ∆x는 병설터널 중심으로부터의 이격거리이다.
Fig. 1에서 병설쉴드터널의 지표침하형상은 선행 및 후행터널 각각의 최대침하량 및 변곡점 거리에 따라 대칭적 형태일 수도 있고, 선행 또는 후행터널 측으로 치우치는 비대칭적 형태일 수 있다. Greenfield condition(미개발 부지 조건)에서 선행터널 굴착 조건은 단선쉴드터널과 동일하므로 대칭적 지표침하형상을 나타내는 것이 일반적이다. 이에 반하여, 터널간 이격거리에 따라 차이가 있으나, 후행터널 굴착 시에는 선행터널의 존재로 인해 선행터널측 지반 변형이 일부 구속될 수 있으며, 선행터널 굴착에 의한 지반 이완영역이 후행터널 굴착에 의한 지반 이완영역과 일부 중첩된다. 또한, 쉴드터널의 지표침하는 쉴드TBM의 챔버압, 굴진율, 뒷채움 그라우팅의 주입량 및 주입압 등과 같은 장비 운영 조건(operational parameter)에 따라 영향을 받으므로(Suwansawat and Einstein, 2007), 선행터널과 후행터널의 굴착 시 장비 운영 차이가 지표침하에 영향을 미칠 수 있다. 이러한 굴착 조건의 차이에 따른 지반거동의 차이는 후행터널에 의한 지표침하형상에 영향을 미치게 된다.
본 연구에서는 후행쉴드터널의 굴착에 따라 추가적으로 발생하는 지표침하형상을 확인하기 위해 현장 지표침하 계측을 수행하였으며, 문헌조사를 통해 Bankok MRT의 후행쉴드터널 굴착에 따른 추가 발생 지표침하를 확인하였다. 그 결과로부터 점성토지반의 후행쉴드터널 굴착에 따라 추가 발생하는 지표침하형상의 특성을 분석하였다.
2. 현장 조건
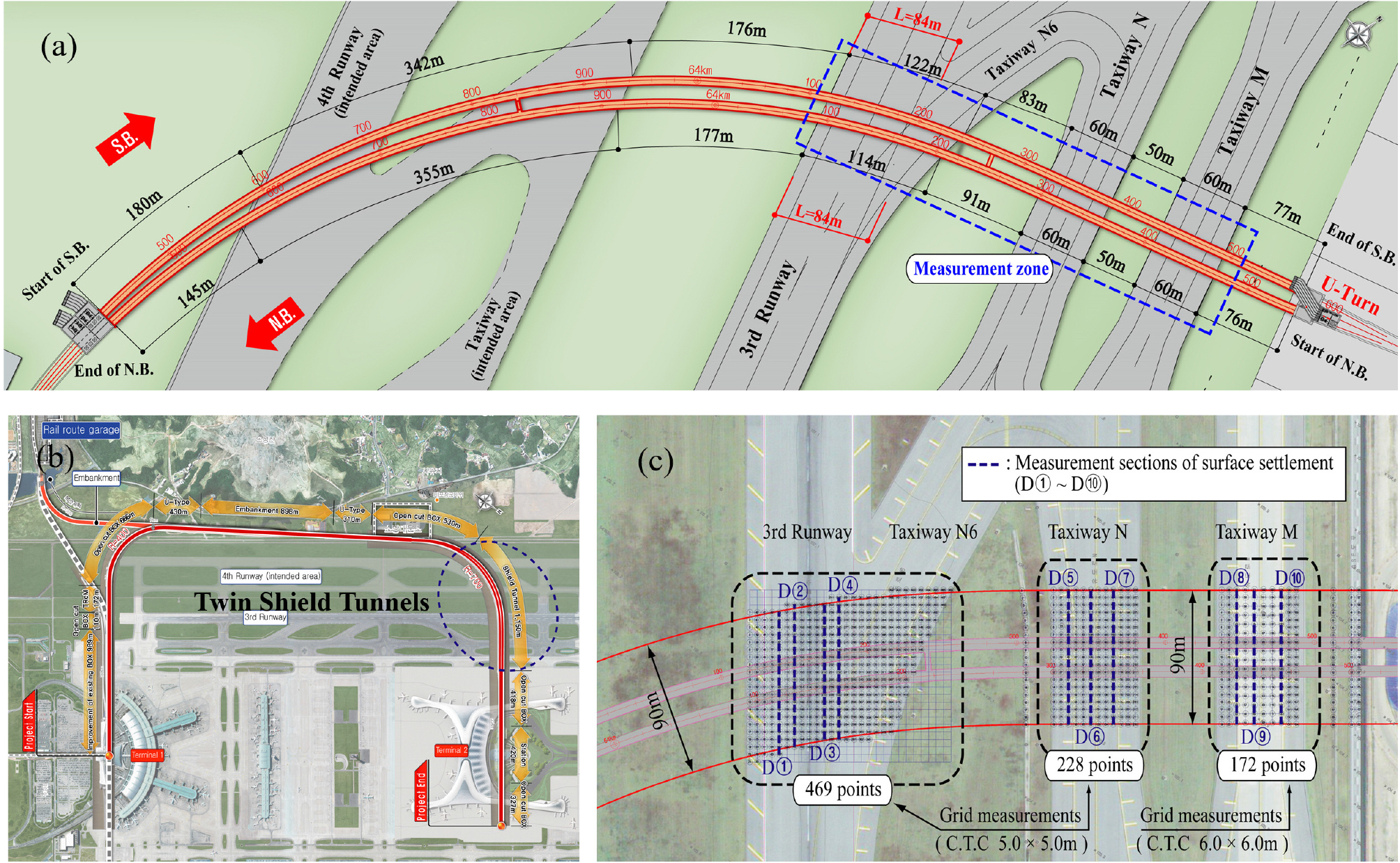
현장 지표침하 계측이 수행된 쉴드터널은 철도터널로써 인천국제공항의 제4활주로 예정부지 및 운영중인 제3활주로와 유도로 N, M 하부로 굴착되었다(이후, T2 연결철도). 쉴드TBM은 외경 7.91m, 길이 9.5m의 EPBs (Earth Pressure Balnaced Shield) Type이고, 터널의 외경과 내경은 각각 7.77m, 7.07m이다. 쉴드터널 중심까지의 심도는 13.3m~22.3m이고, 상행 및 하행선 터널 중심간 거리는 11.4m~20.8m이다. 선행 및 후행의 병설쉴드터널은 1대의 TBM이 시점에서 종점을 왕복하여 시공하였다(Fig. 2(a)).
지표침하형상의 확인을 위한 상세 현장계측은 포장지역(3활주로 및 유도로 N, M)에서 이루어졌으며, 병설쉴드터널 중심으로부터 양쪽으로 각각 45m범위에 대해 정사각형 격자망(c.t.c 5.0m, 6.0m)으로 지표침하를 측정하였다(Fig. 2(c)).
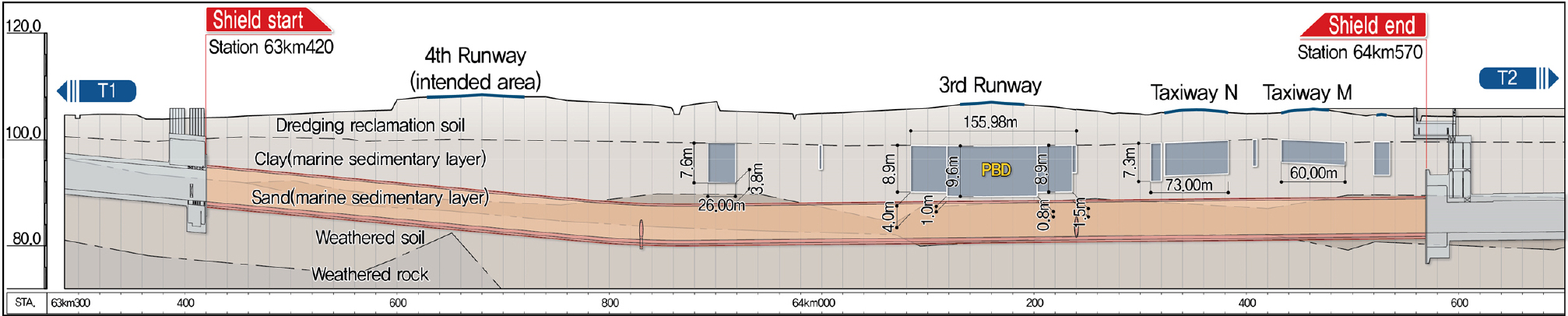
쉴드터널이 시공된 인천국제공항은 서해 경기만에 위치하며, 쥬라기 흑운모 화강암이 기반암으로 분포하고, 상부로 제4기 충적층이 퇴적되어 있다. 과거 빙하기와 간빙기에 의한 해수면의 변화로 인해, 경기만의 퇴적환경이 육지와 바다로 변화되었으며, 이러한 영향으로 점성토와 사질토가 교호하여 퇴적되었다(Korea-National-Railway, 2013a). 쉴드터널의 굴착지반은 점토, 모래, 풍화토이며, 터널 천단부위 부터 상부로 점토층이 분포함에 따라 굴착에 따른 침하는 대부분 점토층에서 발생한다.
3. 후행터널의 지표침하형상 분석
3.1 후행터널의 지표침하
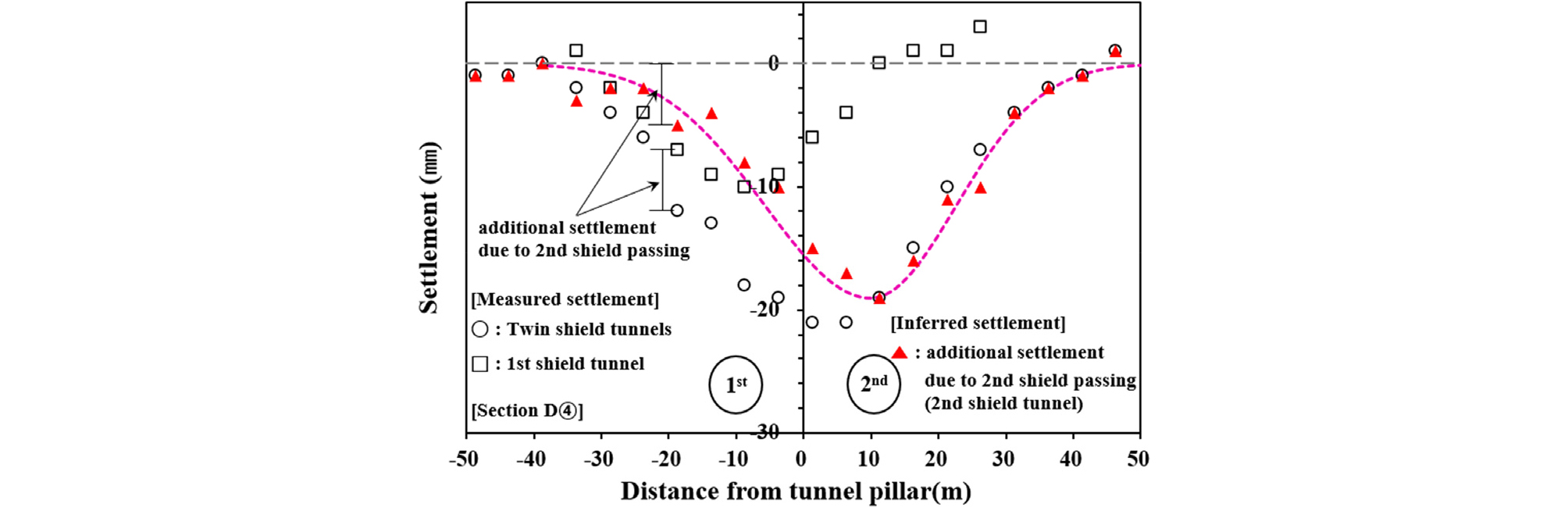
병설쉴드터널에서 직접적으로 계측 가능한 지표침하는 선행터널에 의한 단선쉴드터널의 침하와 후행터널에 의한 병설쉴드터널의 침하이다. 즉, 후행터널에 의해 발생되는 추가 침하는 직접적인 계측이 불가능하다. 따라서, 식 (3)의 중첩원리에 따라 후행터널 굴착에 의해 추가적으로 발생되는 침하는 상기에 언급된 직접적으로 계측가능한 두 침하량의 차이로 유추하여야 한다. Fig. 4는 Fig. 2(c)의 계측단면 D④에서 후행터널에 의한 추가 지표침하를 유추한 예시이다. 여기서, 지표침하계측은 단선쉴드터널과 병설쉴드터널의 지표침하형상 확인을 위해 후행터널 굴착 예상일자의 약 5~30일 이전과 이후 기간에 각각 수행되었다. 항공기 운용 중인 공항 하부에서 터널이 굴착됨에 따라, 지표침하의 직접적인 측정을 위한 터널 상부 활주로, 유도로 진입 가능 시기의 결정에 여러 제약이 있으며, 이로 인해 단면별 계측 일자에 편차가 있다. 3활주로의 경우 선행터널 굴착 후 약 172일에 후행터널이 굴착 되었으며, 후행터널 굴착 이전 약 36일, 굴착 이후 약 33일에 계측을 수행하여 단선쉴드터널과 병설쉴드터널의 침하형상을 각각 계측하였다. 현장 지표침하계측이 수행된 단면 D① ~ D⑩의 후행터널에 의한 추가 침하량을 Fig. 4의 방법으로 유추하였으며, Fig. 6과 7에 나타내었다.
Suwansawat와 Einstein(2007)는 첫번째 굴착터널과 두번째 굴착터널의 Gaussian function의 중첩에 의해 병설쉴드터널의 침하형상을 보다 정확히 표현할 수 있음을 점토지반에 시공된 Bankok MRT의 현장계측결과와 비교를 통해 확인하였다. Suwansawat와 Einstein(2007) 역시 상기의 방법으로 두번째 터널 굴착에 따른 추가 침하량을 유추할 수 있음을 언급하였다.
3.2 후행터널의 지표침하형상 분석
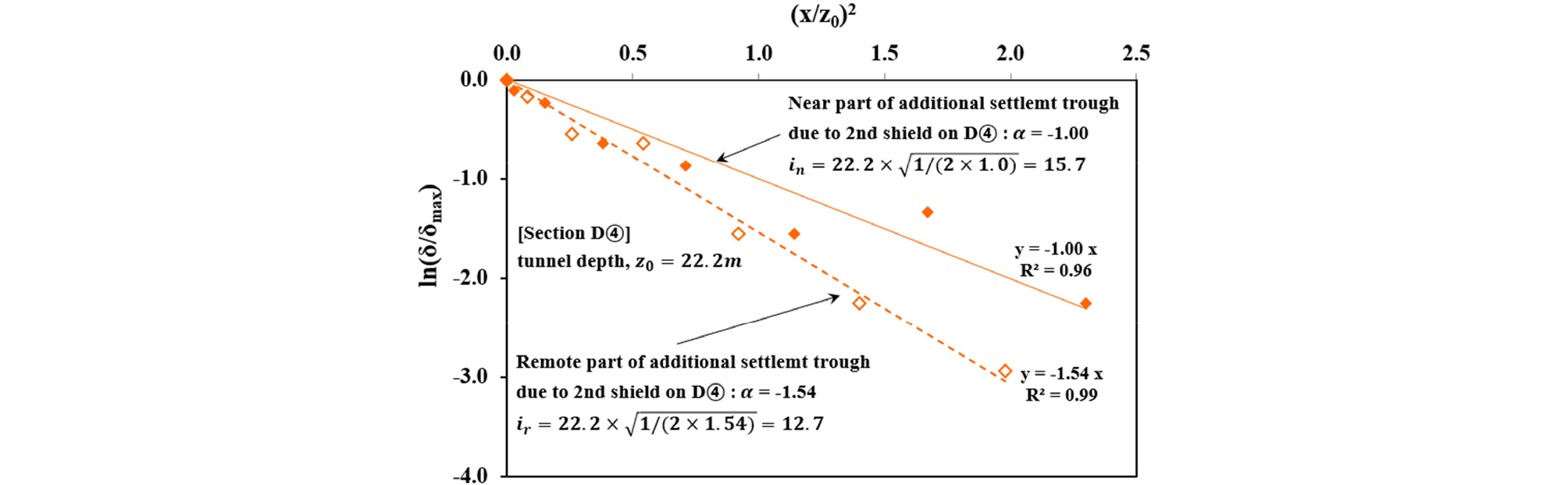
현장계측된 지표침하에 대해 식 (1)의 Gaussian function으로 침하형상을 분석할 때, δmax는 터널 중심위치에서 발생한 계측된 지표침하량을 적용한다. 형상 폭 계수 i는 시행착오법(trial and error method)에 의해 결정하는 방법과 식 (1)의 Gaussian function을 이용하여 결정하는 방법이 있다. 식 (1), (2)로부터 얻어진 식 (4)의 그래프로부터 얻어지는 식 (5)의 기울기 α를 이용하여 식 (6)과 같이 형상 폭 계수 i를 결정할 수 있다.
본 연구에서는 Gaussian function을 이용한 식 (4)와 (6)으로 부터 형상 폭 계수 i를 결정하였으며, Fig. 5는 형상 폭 계수 i의 산정 예시이다. 실측 계측결과를 이용하여 식 (4)와 (6)으로 형상 폭 계수 i를 결정 할 때, Fig. 4의 후행터널 추가 지표침하량 예시와 같이, 계측결과 중 일부에서 지표 융기가 관찰된 경우 융기된 계측치는 제외하고 형상 폭 계수 i를 산정한다.
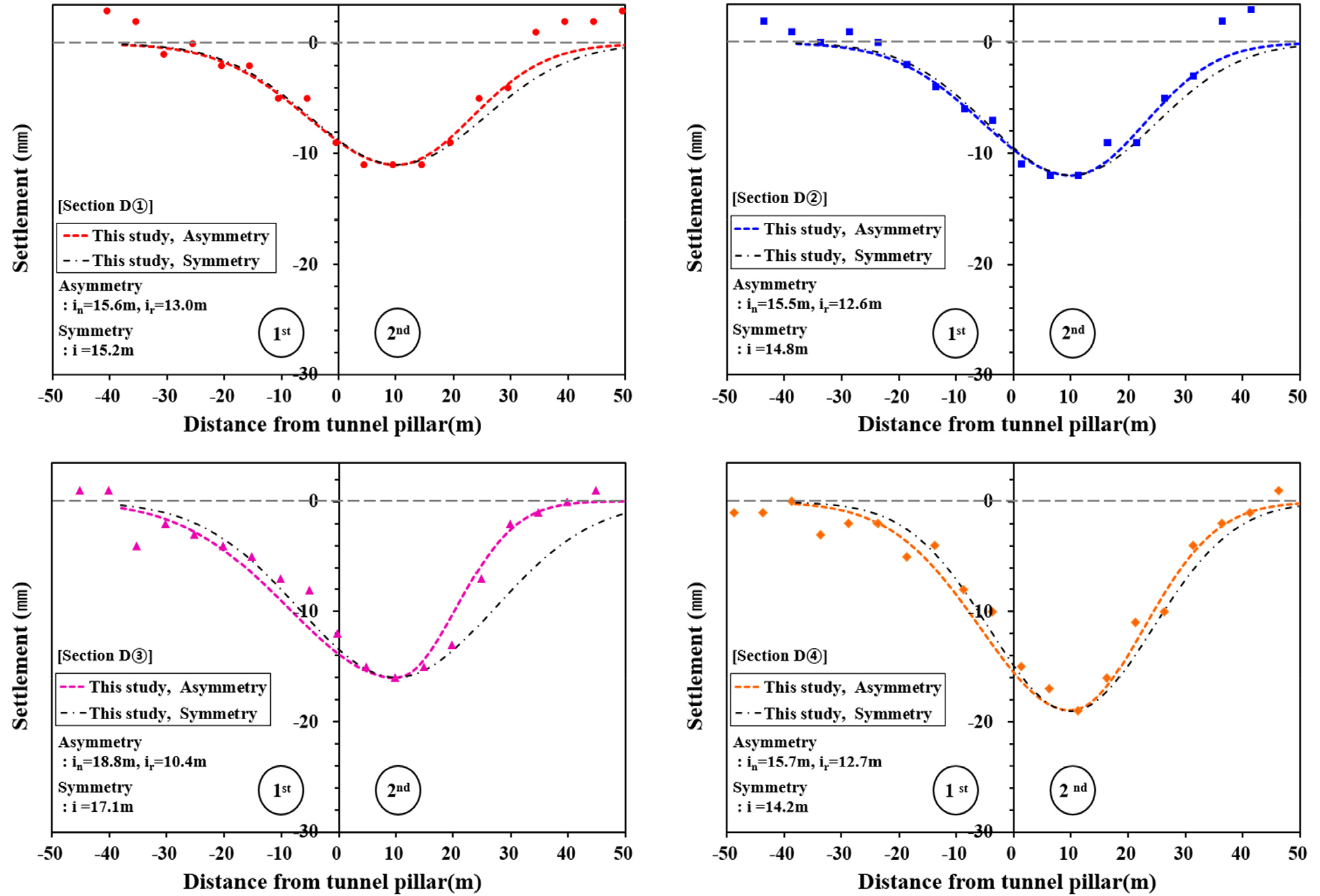
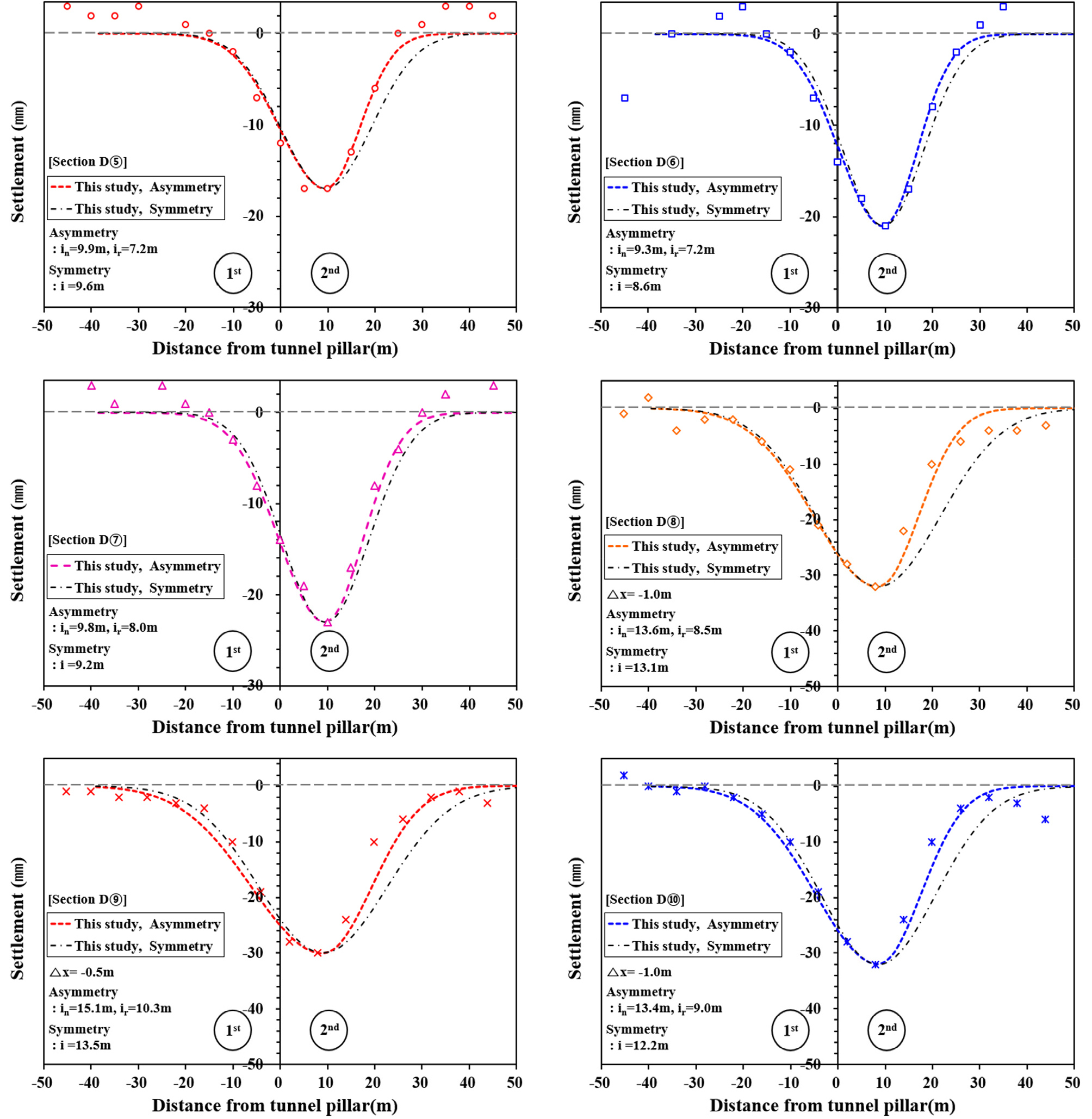
본 연구의 계측단면 D① ~ D⑩의 침하계측 결과, 후행터널 굴착에 따라 추가적으로 발생하는 지표침하형상은 대부분 선행터널측의 폭이 넓은 형상을 나타내고 있다. 이를 명확히 확인하기 위해 침하 계측치와 Gaussian function을 사용한 침하곡선을 Fig. 6과 7에서 비교하였다. 본 연구에서는 침하계측결과를 침하곡선에 보다 효과적으로 반영하기 위해, 후행터널 중심을 기준으로 병설쉴드터널 내측(Near part of twin shield tunnels)과 병설쉴드터널 외측(Remate part of twin shield tunnels)의 형상 폭 계수 in, ir을 각각 산정하여 Gaussian function에 적용함으로써 침하곡선을 표현하였다.
후행쉴드터널의 in, ir을 사용한지표침하곡선은 다음의 순서로 작도할 수 있다.
1. 후행터널의 최대침하량을 기준으로 내측과 외측의 지표침하로 계측결과를 구분한다.
2. 구분된 양측의 침하 계측치로 ln(δ/δmax)와 (x/z0)2의 관계를 각각 나타내고, 이로부터 병설쉴드터널 내측과 외측의 형상 폭 계수 in, ir을 Fig. 5와 같이 각각 산정한다.
3. 계산된 두 개의 i 값을 Gaussian function에 적용하여 침하곡선을 작도한다.
이 방법은 D③, D⑤, D⑧ ~ D⑩와 같이 비대칭성이 큰 경우에도 계측된 침하의 형상을 표현함에 있어 높은 일치성을 나타냄을 확인할 수 있다.
Suwansawat와 Einstein(2007)은 Bankok MRT에서의 현장 계측결과로 부터 병설쉴드터널의 비대칭적 침하형상을 효과적으로 표현하기 위해 각 단선터널의 Gaussian curve를 중첩시키는 방법을 제시하였다. 이때, 후행터널의 침하형상을 본 연구와 다르게 대칭적 Gaussian curve로 가정하였다.
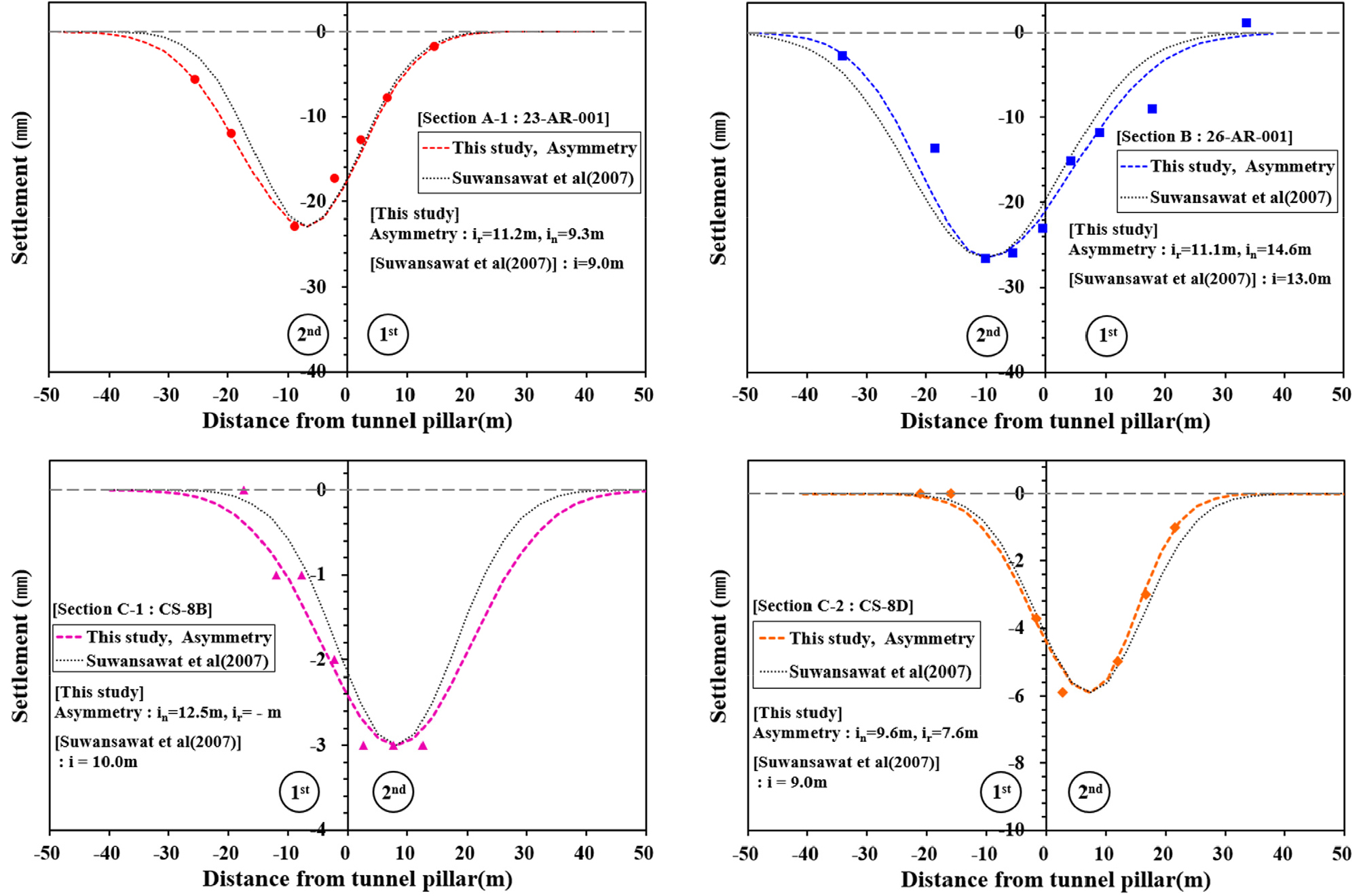
Fig. 8과 9는 Bankok MRT의 현장 계측결과로부터 유추된 후행터널 굴착으로 추가 발생된 지표침하를 본 연구의 in, ir을 사용한 방법에 의한 침하곡선 및 Suwansawat와 Einstein(2007)이 가정한 대칭 침하곡선과 비교한 결과이다. 비교결과 본 연구의 in, ir을 이용한 Gaussian function 침하곡선이 Suwansawat와 Einstein(2007)의 가정보다 후행터널 굴착에 의한 지표침하형상을 효과적으로 표현 할 수 있음을 확인 할 수 있다.
T2 연결철도와 Bankok MRT의 현장 계측결과로부터 유추된 후행터널 굴착으로 추가 발생되는 지표침하형상은 대체적으로 비대칭임을 확인하였다. 또한, 후행터널의 지표침하형상은 내측의 변곡점 거리 in이 외측 변곡점 거리 ir 보다 크고 침하 폭 역시 더 큰 형태를 나타냈다.
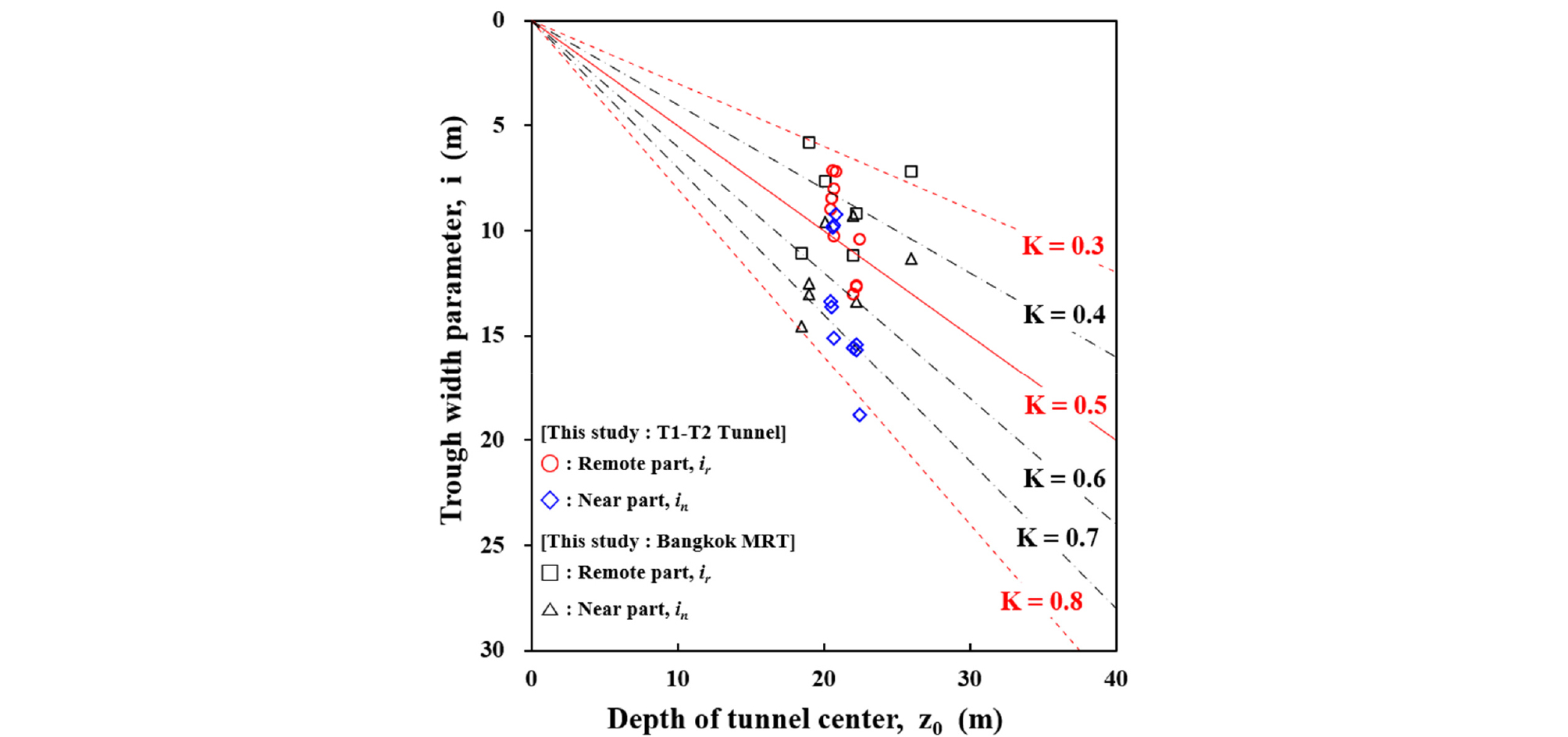
Fig. 10은 점성토 지반에서 후행쉴드터널의 in, ir을 사용한 침하곡선의 경험적 계수 K의 범위를 나타낸 것이다. 침하곡선의 외측 Kr는 0.3~0.6, 내측 Kn는 대부분 0.5~0.8의 범위에 분포하는 것으로 나타났다. 외측의 Kr의 범위 0.3~0.6는 O’reilly와 New(1982) 그리고 Rankin(1988)이 점성토지반의 단선쉴드터널에 대해 제시한 K의 값 0.5를 포함하는 범위이다.
4. 결 론
본 연구에서는 Suwansawat와 Einstein(2007)이 Bankok MRT 병설쉴드터널의 후행터널 지표침하 유추를 위해 사용한 방법을 이용하여, 본 연구에서 수행한 인천국제공항 T2 연결철도 하부 병설쉴드터널의 현장계측 결과로부터 후행터널 굴착으로 추가 발생되는 지표침하를 유추하였다. T2 연결철도와 Bankok MRT의 후행터널의 추가 지표침하의 최대침하량 좌우측에 대해 각각의 in, ir를 산정하여 Gassian function에 적용함으로써, 실측된 후행터널 굴착에 의해 추가 발생된 지표침하형상을 적절히 모사할 수 있었다. 본 연구에 사용된 두 현장의 계측결과에서 후행터널의 내측과 외측의 경험적 계수 K는 외측 Kr는 0.3~0.6, 내측 Kn는 대부분 0.5~0.8의 범위에 분포하였다. 외측 Kr의 범위는 점성토지반에서 단선쉴드터널의 K 값 0.5를 포함하는 범위이다.
본 연구는 일부 현장의 계측결과를 바탕으로 수행한 것으로, 현장 계측결과의 추가 조사, 수치해석 및 모형실험 등에 의한 후행터널의 형상 폭 계수 in, ir에 대한 추가 연구를 통해 중첩의 원리를 이용한 병설터널의 침하형상 예측에 활용 가능할 것으로 판단된다.