1. 서 론
2. 원심모형실험
2.1 실험시스템
2.2 모형지반
2.3 모형 모노파일
2.4 실험조건 및 절차
3. 원심모형실험 결과
3.1 정적재하실험을 통한 극한지지력 산정
3.2 반복수평하중에 대한 거동 평가
3.3 p-y 곡선 비교
4. 결 론
1. 서 론
해상풍력은 육상풍력에 비해 넓은 설치공간과 양질의 풍력 에너지를 안정적으로 생산할 수 있는 이점을 갖고 있어 전 세계적으로 널리 각광받고 있다. 모노파일(monopile)은 해상풍력 발전기의 대표적인 하부기초로 경제성과 시공성이 뛰어날 뿐만 아니라 시공이력과 잘 정립된 설계법으로 널리 활용되고 있다(API, 2011; DNV, 2013). 이러한 이점으로 모노파일은 현재 전 세계적으로 설치된 해상풍력 기초의 약 80% 이상을 차지하고 있다(Murphy et al., 2018). 해상풍력 구조물은 육상구조물에 비해 수직하중(자중)이 작고, 풍력이나 파력, 조력에 의한 횡하중(또는 수평하중)이 크다는 차이가 있다. 따라서, 해상풍력 하부기초 설계 시 횡방향 하중에 대한 충분한 지지력을 확보하는 것이 중요하다.
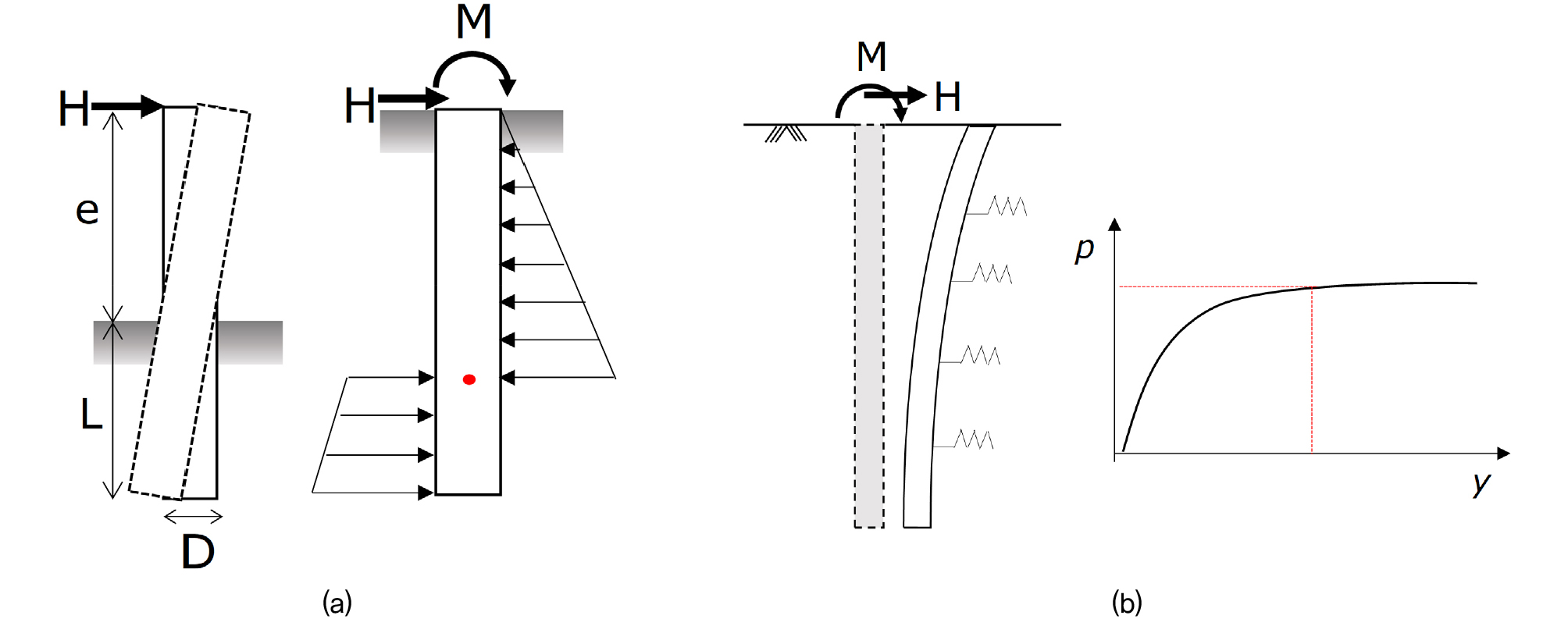
해상풍력 모노파일의 수평거동 해석은 일반적으로 American Petroleum Institute(API)가 제안하고 있는 p-y 곡선법을 사용하고 있다(API, 2011). p-y 곡선법은 수평하중을 받는 말뚝을 해석하는데 가장 널리 쓰이는 방법이다. p-y 곡선법은 말뚝을 탄성보(elastic beam)로 가정해 Fig. 1(a)와 같이 말뚝에 수평하중이 작용했을 때 말뚝과 지반에 각각 휨모멘트와 지반반력이 발생하는 것으로 간주한다. 이때 Fig. 1(b)와 같이 지반을 비선형 스프링(nonlinear spring)으로 치환하여 임의의 깊이에서 지반반력(soil reaction, p)과 말뚝변위(lateral pile displacement, y)의 관계를 나타내어 수평하중에 대한 말뚝거동을 평가한다. 일반적으로 사질토 지반에서의 p-y 곡선은 현행 API에서 채택하고 있는 O’Neill and Murchison(1983)의 p-y 곡선이 사용되고 있다. 또한, 반복하중에 대한 p-y 곡선은 정적하중에 대한 p-y 곡선에서 극한지반반력에 90%에 해당하는 곡선을 사용하고 있다.
한편, API p-y 곡선법은 제한된 지반조건에서 직경 1m 미만인 소구경 말뚝의 현장시험 기반으로 개발되었기 때문에 모노파일과 같은 대구경 말뚝에 적용하는데 한계가 있다(Choo and Kim, 2015). 뿐만 아니라, 횡방향 장기반복하중에 의한 말뚝거동이 다양한 인자(하중크기, 반복하중 횟수, 지반조건 등)에 복잡하게 영향을 받음에도 불구하고, p-y 곡선에서는 감소계수를 일률적으로 적용하고 있어 말뚝거동을 정확히 예측하는데 한계가 있다(Achmus et al., 2009; Paik et al., 2011; Choo and Kim, 2015; Murphy et al., 2018; Lee et al., 2019; Baek et al., 2019; Lee et al., 2020; Li et al., 2023).
최근 모노파일의 정적하중에 대한 횡방향 거동평가는 주로 원심모형실험과 수치해석을 통해 수행되고 있다. Lee et al.(2020)은 비교적 느슨한 포화 모래지반(상대밀도, Dr = 52%)에 근입된 직경 7m 모노파일의 횡방향 거동을 평가하기 위해 원심모형실험을 수행하였으며, 지표면으로부터 수평하중 재하높이가 모노파일의 수평거동에 미치는 영향이 미미하다는 것을 확인하였다. Choo and Kim(2015)은 조밀한 모래지반(Dr = 85%)에 근입된 직경 6m 모노파일에 대해 횡방향 재하실험을 수행하였으며, API p-y 곡선이 초기 기울기 및 지반반력을 과대평가하고 있는 것을 확인하였으며, 실험결과를 기반으로 조밀한 모래지반에서 대구경 모노파일에 대한 p-y 곡선을 제안하였다.
반복하중에 대한 모노파일의 횡방향 거동평가도 활발히 이루어지고 있다. Lee et al.(2019)은 원심모형실험을 통해 조밀한 건조 모래지반에서 직경 3.3m 모노파일에 대해 양방향(two-way) 반복하중 조건에서의 횡방향 거동을 평가하였으며, API p-y 곡선이 초기 기울기를 과대평가하는 것을 확인하였다. 또한, Baek et al.(2019)은 조밀한 포화 실트질 모래지반(Dr = 70%)에서 양방향 반복수평하중을 받는 말뚝의 거동을 평가하였으며, 반복하중 횟수가 증가할수록 말뚝 인접지반의 조밀화로 인해 지반반력이 증가하는 것을 확인하였다. 또한, 최초 10회 이하의 반복하중이 작용할 때 반복하중에 의한 p-y곡선의 강성감소효과가 가장 크게 나타났으며, 이후 그 효과가 점차 미미해지는 것을 확인하였다.
한편, Achmus et al.(2009)는 유한요소해석을 통해 조밀한 모래지반 조건에서 직경 7.5m의 대구경 모노파일에 대해 횡방향 거동을 분석하였으며, 수평하중을 받는 모노파일의 영구변위는 모노파일의 직경보다 깊이에 크게 영향을 받는 것을 확인하였다. 또한, Murphy et al.(2018)는 수치해석과 현장시험을 통해 정적 수평하중을 받는 직경 0.5m인 소구경 모노파일의 수평거동을 분석하였으며, 수평변위를 예측하는 방법론을 제시하였다. 이 외에도 Kim et al.(2014)은 실트질 모래지반에서 반복하중을 받는 해상풍력 모노포드(monopod)와 트라이포드(tripod)의 거동을 평가한 바 있으며, 극한하중보다 작은 반복하중 조건에서 반복하중에 의한 영구변위가 미미함을 확인한 바 있다.
최근 수행된 선행연구들에서 나타난 바와 같이 해상풍력 모노파일의 반복수평하중에 대한 거동이 하중크기, 하중횟수, 하중조건(one-way or two-way) 등에 복잡한 변수에 복잡하게 영향을 받음에도 불구하고, 현재까지 제한적인 조건으로만 연구가 수행된 실정이다. 뿐만 아니라 국내 서남해안 인근에 널리 분포하는 실트질 모래지반에서 모노파일의 반복수평하중 거동평가는 매우 부족하므로 실트질 모래지반에 설치된 모노파일의 반복수평하중 거동에 대한 추가적인 실험적 연구가 필요하다. 따라서, 본 연구에서는 원심모형실험을 이용해 느슨한 포화 실트질 모래지반에서 해상풍력 대구경 모노파일의 양방향 반복수평하중에 대한 원심모형실험을 실시하였으며, API에서 제안하는 p-y 곡선 및 선행연구와 비교하였다. 실험 결과는 서남해안 지역과 같이 실트질 모래지반이 널리 분포하는 지반조건에서 모노파일의 장기거동을 평가하고 기존 p-y 곡선과 비교하는데 큰 의의가 있다.
2. 원심모형실험
2.1 실험시스템
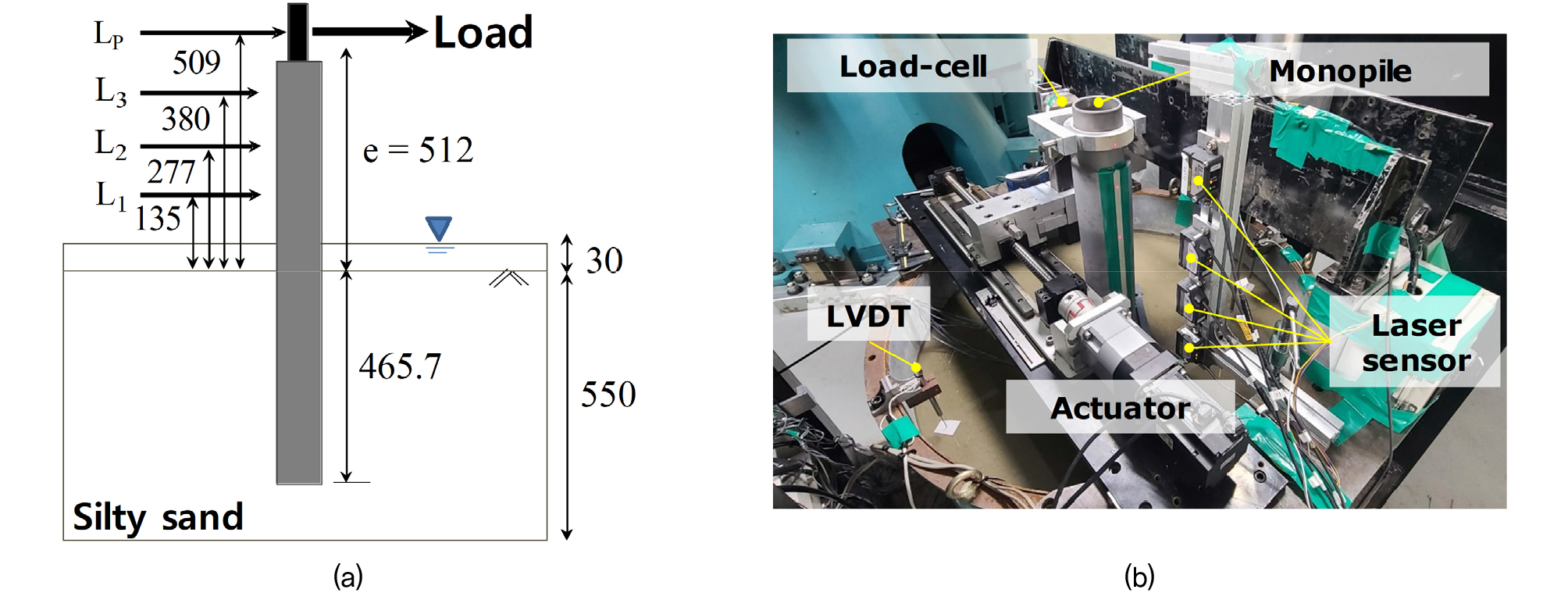
본 연구는 KAIST 지오센트리퓨지센터(KOCED)에 설치된 240g·ton 용량의 원심모형실험기를 활용하였다(Kim et al., 2013). 본 실험을 위해 대구경 모노파일의 수평거동 분석을 위한 실험시스템을 구성하였다(Fig. 2). 이를 위해 내경 900mm, 높이 700mm의 원형 강재(steel)로 된 토조 상단에서 모노파일에 수평하중을 재하 할 수 있는 수평엑츄에이터를 설치하고, 변위제어방식으로 모노파일에 수평방향 반복하중을 재하할 수 있도록 하였다. 하중제어 방식의 경우 수평하중을 재하 할수록 누적변위가 발생하며(Lee et al., 2019; Zhu et al., 2021), 변위제어의 경우 변위를 재하 할수록 지반상태 변화로 인해 작용하는 하중이 변화하는 특징이 있다(Darvishi Alamouti, S, 2019; Choo and Kim, 2015; Lee et al., 2020). 두 방식은 하중특성과 누적변위 관점에서 결과에 차이를 발생시키며, 본 연구는 변위제어로 수행되었으므로 실험 결과는 변위제어 방식의 결과에 국한된다.
축소된 모노파일에 수평하중 재하 시 변위 및 회전각을 관측하기 위해 Keyence 사의 IL-300 비접촉식 레이져센서(Laser sensor)를 활용하였다. 이때, 모노파일의 길이방향으로 4개 지점에 레이져센서 타겟을 설치하고 횡하중에 대한 변위를 관측하였다. 또한, 모형 모노파일 상부에 설치된 압축/인장형 로드셀(Load cell, Tokyoshokki 사의 TCLK 10KNA)을 통해 수평하중 재하 시 모노파일에 작용하는 하중을 측정하였다. 뿐만 아니라, 원심모형실험 중 지반의 침하를 계측하기 위해 모형 토조 벽면에 linear variable differential transducer(LVDT) 2개를 설치하였다.
모노파일에 수평하중을 재하하기 위해 수평엑츄에이터 구동부에 랏드(rod)를 고정하고, 랏드 끝단에 모노파일과 최소한의 유격으로 삽입시킬 수 있는 연결링을 설치하였다. 연결링은 힌지 타입(hinge type)으로 제작하여 수평하중에 의해 모노파일이 회전할 때 연결부에 국부적으로 발생하는 휨모멘트를 최소화 하도록 했다. 또한, 연결링 내부(연결링과 모노파일이 맞닿는 부분)를 테프론(teflon)으로 제작하여 하중이 재하되는 동안 마찰이 발생하는 것을 최소화하였다. Fig. 2는 센서의 위치와 실험시스템을 보여준다.
2.2 모형지반
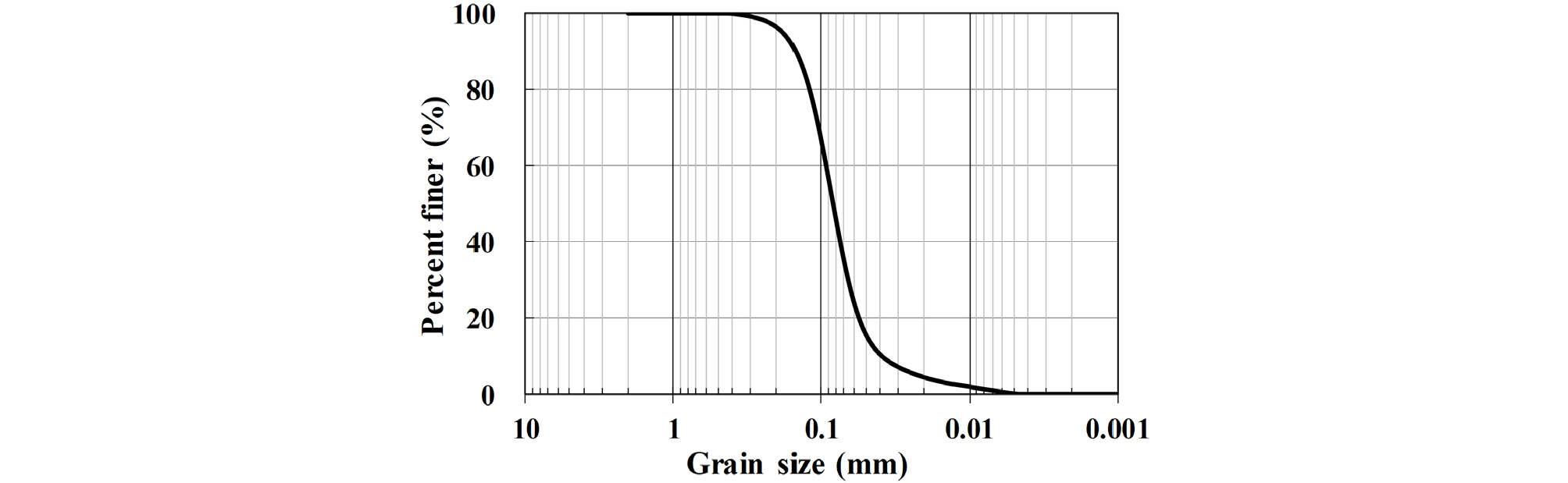
본 연구에서는 국내 대규모 해상풍력 단지 개발 예정 부지인 서남해안 새만금지역에서 채취한 흙을 모형지반으로 선정하였다(Kim et al., 2014). 새만금 흙은 비중(Gs) 2.67이며, 평균 유효입경(D50) 0.08mm로 통일분류법(unified soil classification system, USCS)상 실트질 모래지반(SM)으로 분류된다. 채취된 새만금 흙의 입도곡선은 Fig. 3과 같으며, 기본 물성치는 Table 1과 같다.
Table 1.
Basic soil properties of Saemangeum sand
| Items | Properties |
| Soil classification (USCS) | SM |
| Specific gravity (Gs) | 2.67 |
| Friction angle (°) | 35.8 (Kim, 2016) |
| Maximum dry density (kg/m3) | 1,650 |
| Minimum dry density (kg/m3) | 1,200 |
본 연구에서는 상대밀도(Dr) 40%의 느슨한 사질토를 조성하기 위해 모형지반을 11층으로 나누어 분할 다짐하였다. 이때 각 층의 균질성을 확보하기 위해 층 높이를 5cm로 균일하게 하였으며, 목표 밀도에 해당하는 흙을 최적함수비(optimal moisture content) 18.4%로 교반한 뒤 토조에 투입 후 층다짐을 실시하였다. 마지막 층을 조성 한 후에는 지표면으로부터 소량의 물을 흘려 물이 시료 내부로 침투되도록 유도하였으며, 지표면으로부터 3cm 수위가 될 때까지 물을 가득 채운 뒤, 4주 이상 방치하여 지반포화(soil saturation)를 유도하였다. 원심모형실험 중 지반의 침하량을 LVDT를 통해 관측한 결과, 원심가속도의 증가로 초기 지반의 상대밀도인 Dr = 40%에서 Dr = 47%로 일부 증가하는 것을 확인하였다.
2.3 모형 모노파일
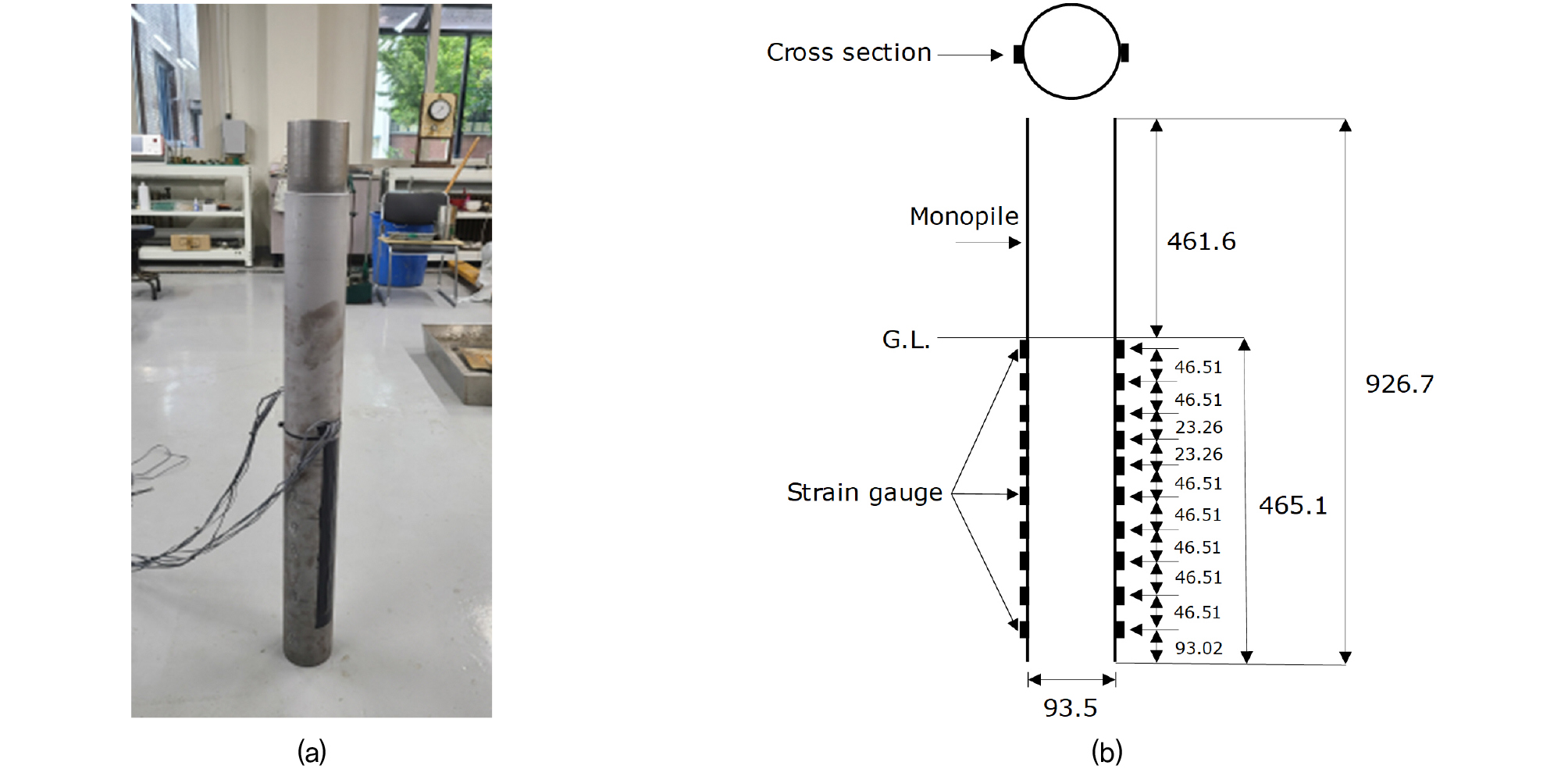
본 연구에서는 직경 6m급 해상풍력 모노파일을 대상으로 축소모델링을 실시하였다. 모형은 강재(steel)로 제작하였으며, 원심모형상사비(1/64.5)를 고려하여 외경(Do,m)은 93.5mm, 내경(Di,m) 90.96mm, 길이(Lm) 926.7mm, 근입깊이(zm) 465.1mm, 선단부 두께(tm) 0.0013mm로 제작하였다. 이는 원형스케일로 환산하였을 때, 각각 직경(Do,p) 6m, 길이(Lp) 63m, 근입깊이(zp) 30m, 두께(tp) 0.082m에 해당되며, 모노파일 직경 대비 선단부 두께비(Do,p/tp)는 73.6이다. 일반적으로 현장에서 사용되는 모노파일의 직경(Do,p) 대비 선단부 두께비(Do,p/tp)가 25~100 이내인 것을 감안할 때 제작된 모노파일의 두께비는 일반적인 범위에 속한다. 가공된 모노파일은 표면이 매끄러워 실제 모노파일의 표면 거칠기를 모사할 수 없으므로, 제작된 모노파일 표면에 샌드블래스팅(sand blasting)으로 처리하여 거친 표면을 모사하였다. 이후, 조도계를 통해 표면 거칠기를 측정하였으며, 평균 거칠기(Ra)는 1.14μm로 확인되었다.
Uesugi et al.(1990)는 강재와 흙입자 사이의 거칠기비(Ra/d50)에 따른 마찰계수 범위를 제안하였으며, 이를 토대로 본 연구에서 제작된 모노파일의 마찰계수가 0.5~0.55인 것으로 확인하였다. 일반적인 강관과 지반사이의 마찰계수가 0.53~0.57인 것을 감안하면, 제작된 모형 모노파일이 합리적으로 지반-모노파일의 상태를 모사할 것으로 판단된다. 한편, 본 실험은 단단한 벽체(rigid wall)로 둘러쌓인 토조에서 수행되었으며, 벽체가 모노파일 거동에 영향을 미치는 경계면 효과(boundary effect)가 발생할 수 있다(Li et al., 2023). Frick and Achmus(2020)은 수치해석을 통해 느슨한 사질토 지반에서 모노파일 직경대비 경계면까지의 거리(S/Do,m, 여기서 S는 모노파일 중심부터 벽체까지의 거리, Do,m은 모형 모노파일 외경)가 5 이상일 때 경계면 효과가 미미함을 확인하였으며, Prakasha et al.(2005)는 경계면 효과를 최소화하기 위해서는 S/Do,m이 4 이상이 되어야 한다고 하였다. 본 연구는 S/Do,m = 4.81의 조건에서 수행되었으며, Prakasha et al.(2005)의 기준을 충족하므로 모노파일의 횡하중-변위거동에 미치는 영향이 미미할 것으로 판단된다. Table 2는 모형 모노파일 및 상사비를 적용한 원형 모노파일의 상세제원을 나타낸다.
Table 2.
Monopile specification
실트질 모래지반에 설치된 모노파일의 횡방향 하중에 대한 거동을 평가하기 위해 모노파일의 길이방향으로 변형률계(strain gauge)를 설치하였다. 이때, 지반에 근입된 모노파일의 위치별 거동을 관측하기 위해 지표면으로부터 0D, 0.5D, 1D, 1.5D, 1.75D, 2D, 2.5D, 3D, 3.5D, 4D 깊이(여기서 D는 모노파일 외경)에 180° 방향으로 총 10쌍의 변형률계를 설치하였다. 변형률계는 모노파일 설치 중 응력집중과 단선을 막기 위해 피복이 없는 얇은 에나멜 연선(enamelled winding wires)으로 연결되었으며, 차수를 위해 표면에 Vishay사의 M-coat A를 여러 차례 도포한 뒤, VM 테이프로 겉면을 2차 차폐하여 실험 중 센서 망실을 최소화했다. 실험 중 계측된 변형률을 통해 깊이별 모멘트로 환산하여 모노파일에 작용하는 휨모멘트를 도출하였다. Fig. 4는 모형 모노파일 및 변형률계가 설치된 모노파일의 단면도를 나타낸다.
2.4 실험조건 및 절차
제작된 시스템과 모형을 이용해 느슨한 실트질 모래지반에 설치된 해상풍력 모노파일의 정적 및 양방향 반복수평하중에 대한 원심모형실험을 수행하였다. 우선, 느슨한 실트질 모래지반에 설치된 모노파일의 극한하중(ultimate load state, ULS)을 산정하기 위해 정적하중재하실험을 수행하였다.
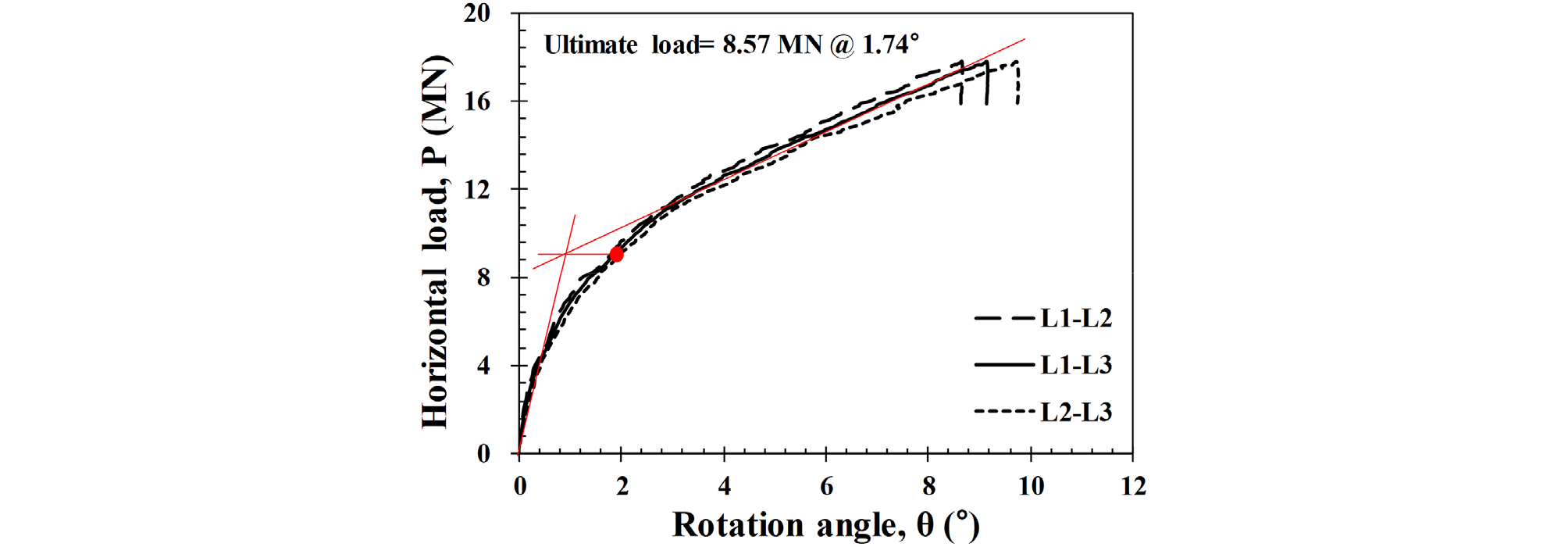
이를 위해 지반조성이 완료된 토조 상부에 수평엑츄에이터를 설치하였으며, 안정적인 하중재하를 위해 하중재하장치와 토조를 강결시켰다. 그 후 변형률계가 설치된 모형 모노파일을 토조 중앙에 일정한 속도로 압입 설치한 후 원심모형실험 바스켓에 거치한 뒤, 모노파일 상부에 수평하중을 재하하기 위한 연결링과 관측을 위한 센서를 설치하였다. 실험을 위해 목표 중력가속도인 64.5g까지 3g/min으로 가속하였으며, 목표 중력가속도에서 지반안정화를 유도한 뒤, 정적하중재하실험을 실시하였다. 수평하중재하는 1mm/s의 일정한 속도로 변위를 제어하였으며, 이때 센서를 통해 계측된 결과들을 토대로 모노파일의 하중-변위 곡선을 도출하고, 극한하중을 산정하였다.
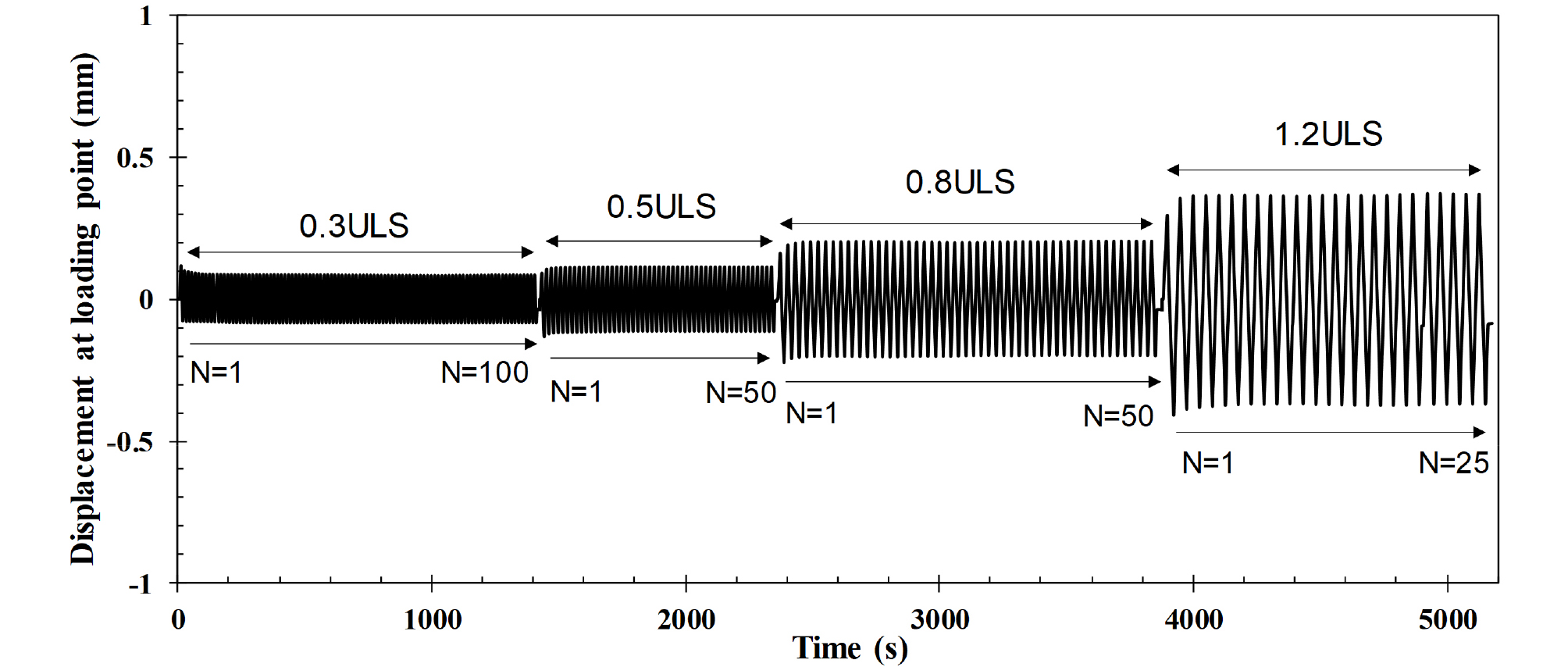
극한하중은 모노파일의 하중-회전각 곡선에서 초기 탄성부분 접선과 항복 이후 소성구간의 접선이 서로 만나는 점을 기초의 극한하중(ultimate limit state; ULS)으로 산정하였다(Villalobos, 2006). 그 결과, 극한하중은 1.74° 회전각에서 8.57MN로 확인되었으며, 산정된 극한하중을 통해 모노파일에 작용할 반복하중의 크기를 산정하였다(Fig. 5). 반복하중의 크기는 정적하중재하실험을 통해 획득한 극한하중(ULS)의 30%(0.3ULS), 50%(0.5ULS), 80%(0.8ULS), 120%(1.2ULS)를 각각 산정하였으며, 정적하중재하시험과 동일한 시료로 재성형하여 조성 한 뒤, 작은 하중부터 큰 하중에 이르기까지 단계적으로 반복하중재하실험을 수행하였다. 본 연구에서는 변위제어 방식의 수평하중 재하장치를 사용하였으므로, 정적하중재하실험을 통해 도출된 하중-변위곡선에서 각각 0.3ULS, 0.5ULS, 0.8ULS, 1.2ULS의 하중에 해당하는 변위를 확인한 뒤, 반복하중재하실험에서 각 하중에 해당하는 변위만큼 이동시켜 목표하중을 재하하는 방식을 택하였다. 각 실험에서 반복횟수(Ncycle)는 각각 100회(0.3ULS), 50회(0.5ULS), 50회(0.8ULS), 25회(1.2ULS)로 설정하였다(Table 3).
Table 3.
Testing condition
| No. | Static load | Cyclic load case | |||
| Loading state | ULS* | 0.3ULS | 0.5ULS | 0.8ULS | 1.2ULS |
| Load level (MN) | 8.57 | 2.57 | 4.29 | 6.86 | 10.28 |
| Cycle number (N) | - | 100 | 50 | 50 | 25 |
상세 실험절차는 다음과 같다.
(1) 조성된 모형지반에 변형률계가 설치된 모형 모노파일을 수직하중 재하장치를 이용해 압입설치한다. 이때, 정확한 수평거동 해석을 위해 관입 중 경사계를 통해 수직도가 유지되는지를 확인하였으며, 목표 관입깊이인 465.1mm까지 압입한다.
(2) 토조 상단에 수평하중 재하장치를 설치한 뒤, 모노파일의 변위 및 회전각 측정을 위한 레이져센서를 지표면으로부터 각각 135mm(L1), 277mm(L2), 380mm(L3), 509mm(LP, 수평하중 재하위치) 높이에 설치한다. 또한, 수평엑츄에이터를 이용해 모노파일에 수평하중을 재하하기 위해 엑츄에이터의 가력부가 지표면으로부터 512mm 높이(원형기준 33m)에서 모노파일에 수평하중을 재하시킬 수 있도록 하였다.
(3) 모형토조를 원심모형실험기에 탑재한 후 3g/min의 속도로 목표 중력가속도인 64.5g까지 가속한다.
(4) 목표 중력가속도에서 지반이 안정화된 후, 낮은 크기의 반복하중(0.3ULS)부터 높은 크기의 반복하중(1.2ULS)까지 순서대로 단계적으로 하중을 재하한다. 이때, 반복수평하중은 변위제어 방식을 통해 하중재하 지점에서 1mm/s의 일정한 속도로 재하되었으며, 정적하중재하시험에서 산정된 하중-변위 곡선을 통해 목표 반복하중 크기에 해당하는 변위를 기준으로 반복하중을 재하하였다.
3. 원심모형실험 결과
3.1 정적재하실험을 통한 극한지지력 산정
Fig. 5는 수평하중에 대한 모노파일의 하중-회전각 곡선을 나타낸다. 이때, 회전각은 모노파일 길이방향으로 각 위치에 설치된 레이져센서를 통해 산정하였다. 그 결과, 회전각 산정에 사용된 센서의 위치에 관계없이 유사한 하중-회전각 거동을 보였다. 이는 지표면 위로 노출된 모노파일이 작용한 하중범위 내에서 강체거동(rigid body)을 보임을 의미하며, 이후 해석에서는 L2 - L3의 센서를 통해 산정된 값을 대표 회전각으로 선정하였다.
수평하중이 재하될 때 모노파일의 길이 방향으로 외벽에 설치된 변형률계(strain gauge)를 통해 모노파일에 작용하는 위치별 휨모멘트를 관측하였다. 이때, 모노파일의 180° 방향으로 설치된 변형률계의 관측값을 통해 모노파일에 작용하는 휨 변형률을 식 (1)을 이용해 산정하였다. 관측된 변형률에서 휨모멘트는 식 (2)를 이용해 산정할 수 있다.
여기서, 은 모노파일에 작용하는 휨 변형률, , 은 모노파일 중심축 기준 180° 방향에 설치된 변형률계 관측값을 의미한다. 산정된 값과 모노파일 제원을 통해 횡하중에 의해 발생하는 휨모멘트()는 다음과 같은 식을 통해 산정된다.
여기서, = 휨모멘트, = 모노파일의 탄성계수, = 단면계수
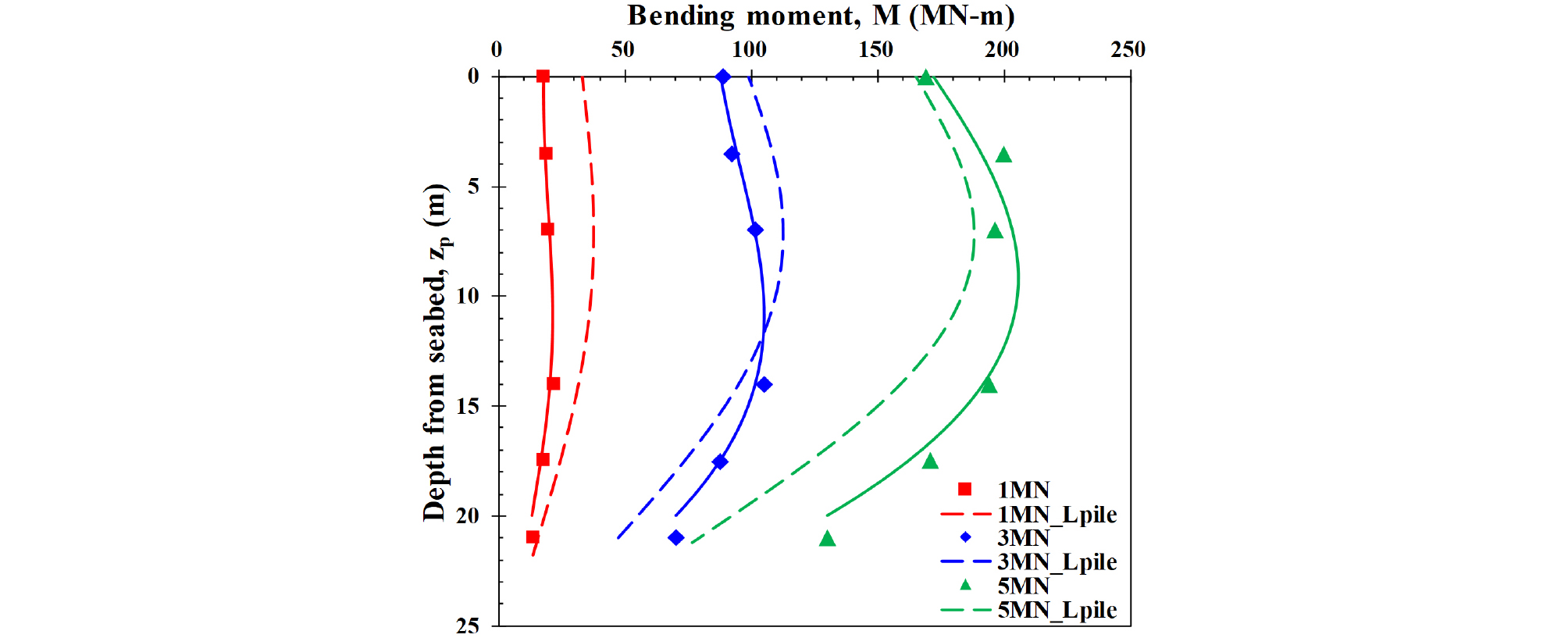
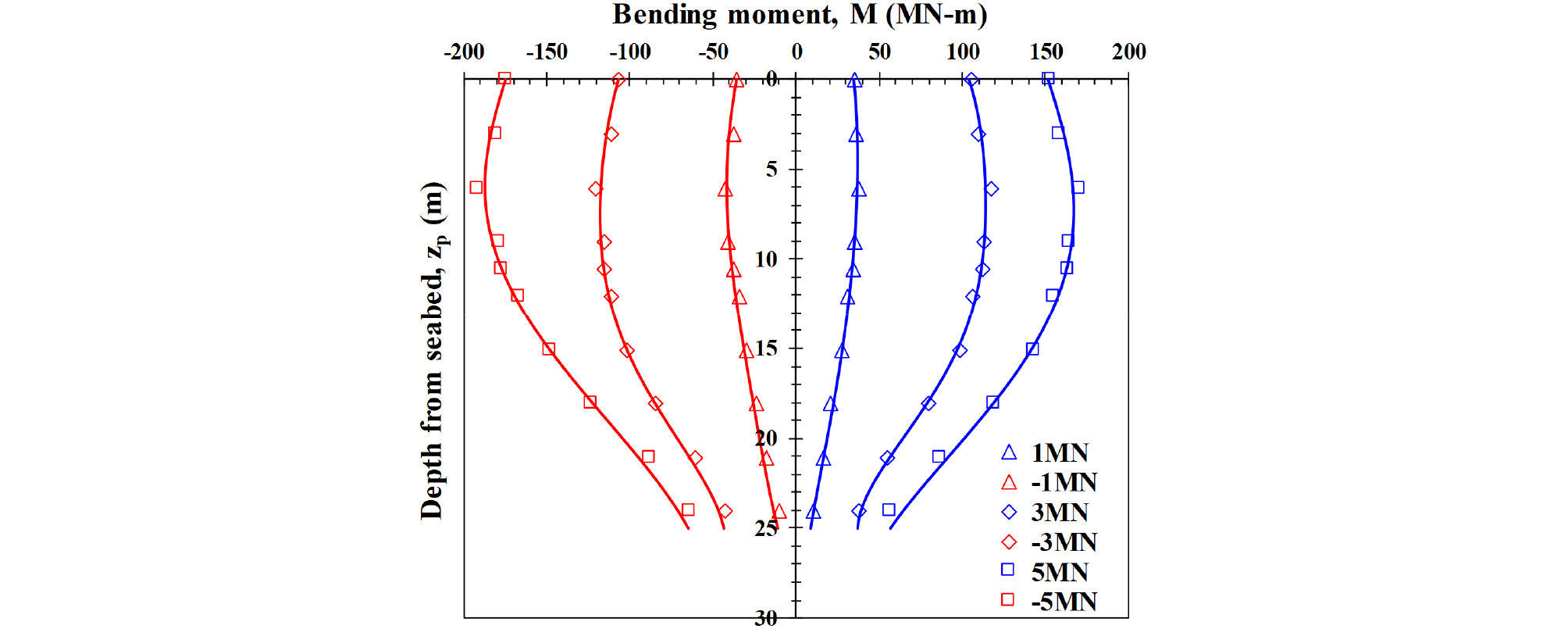
관측된 휨모멘트는 원심모형실험 상사법칙인 N3(여기서, N은 원심가속도)을 고려해 원형(prototype)으로 환산하였다. Fig. 6은 정적수평하중 1MN, 3MN, 5MN에서 모노파일에 설치된 변형률계(strain gauge)를 통해 계측된 휨모멘트를 회귀곡선(regression curve)과 함께 나타내었다. 회귀곡선은 식 (3)과 같이 5차 다항식(5th polynomial)을 이용하였으며, 깊이방향으로 특정하중에서 관측된 휨모멘트를 회귀분석에 활용하였다. 여기서, 은 휨모멘트, 은 피팅계수, 는 깊이를 의미한다. 이때, 5차 다항식인 식 (3)의 2차항은 깊이별 휨모멘트의 이계미분을 통해 도출되는 지반반력(p)이 지표면에서 0이 되도록 하기 위해 2.5제곱으로 치환하여 사용하였다(Kong and Zhang, 2006; Choo and Kim, 2015; Lee et al., 2020). 산정된 회귀곡선은 전반적으로 실험값과 높은 상관관계성을 가지고 있음을 확인하였다.
실험 결과, 모노파일에 작용하는 휨모멘트는 지표면으로부터 깊이가 깊어질수록 증가하다가 10m 깊이(z/D = 1.67)에서 최댓값을 나타내었다. 이후, 깊이가 깊어질수록 휨모멘트가 감소하였다.
모노파일의 수평거동 분석 및 원심모형실험 결과의 검증을 위해 말뚝 전용 1차원 유한차분법 해석 프로그램인 L-pile을 활용하였다(L-pile, 2022). L-pile은 현행 API p-y 곡선이 탑재되어 있어 수평거동 말뚝을 분석하는데 유용하다. 본 연구에서 사용된 L-pile 지반조건은 API sand이며, 말뚝은 모노파일과 같은 강관말뚝을 모사하기 위해 steel pipe pile 요소를 사용하였고, 탄성계수는 210 GPa로 실험에 사용된 강재의 특성을 반영하였다. 상세 해석조건은 Table 4와 같다. 수평하중은 모노파일 상단(지표면으로부터 33m 지점)에 1MN, 3MN, 5MN을 각각 재하하였다. L-pile을 통해 수평하중에 따라 모노파일에 발생하는 휨모멘트도를 Fig. 6과 같이 도출하였으며, 원심모형실험에서 획득한 값과 비교해 본 결과, 전반적으로 유사한 결과를 얻을 수 있었다.
Table 4.
Input parameters of L-pile
3.2 반복수평하중에 대한 거동 평가
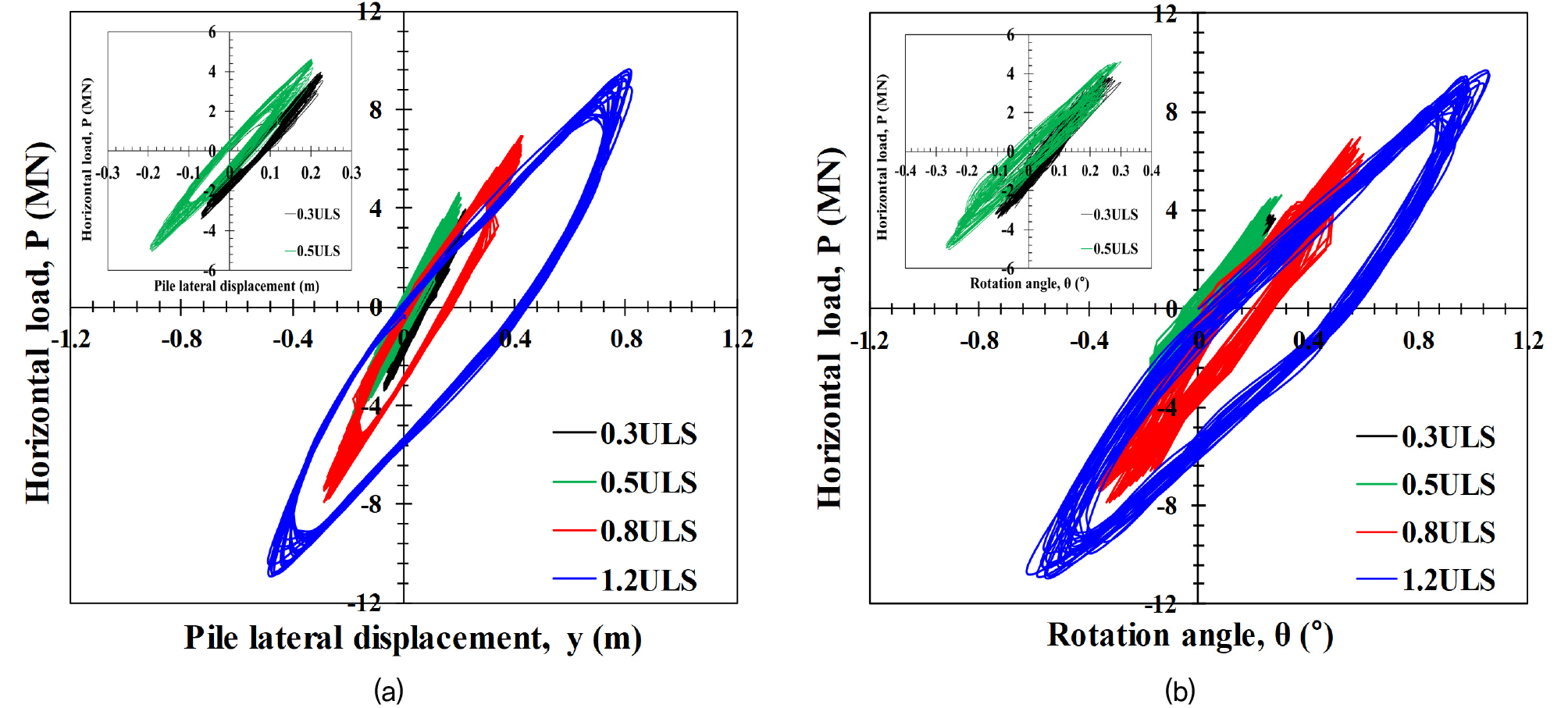
정적하중 실험을 통해 산정한 극한하중을 토대로 반복하중 크기를 선정해 반복수평하중 실험을 수행하였다. 이때, 모노파일에 작용한 반복하중은 Fig. 7과 같이 0.3ULS부터 1.2ULS까지 단계별로 재하(stage test)하였다. 본 연구에서는 수평엑츄에이터를 이용해 하중 재하지점에 일정한 속도(1mm/s)로 변위를 유발시켜 톱니모양의 반복하중이 재하되도록 했다. 따라서, Fig. 7과 같이 하중 크기가 커질수록 주기가 길어지는 것을 확인할 수 있다. Fig. 8은 모노파일의 반복수평하중 실험에서 도출된 하중-변위, 하중-회전각 곡선을 각 조건별로 보여준다. 실험 결과, 양방향 반복수평하중이 재하됨에 따라 하중-변위 곡선과 하중-회전각 곡선이 타원 형상(ellipse loop)을 나타내는 것을 확인하였다. 또한, 낮은하중에서는 선형거동을 보이나 반복수평하중의 크기가 커질수록 하중이력 곡선을 둘러싼 타원 면적(hystrerysis loop)이 커졌다. 뿐만 아니라, 하중이 증가함에 따라 타원의 기울기가 점차 완만해 지는 것을 알 수 있다. 이는 하중이 증가함에 따라 지반의 비선형성(non-linearity)과 영구변형의 크기가 커지기 때문인 것으로 판단된다.
Fig. 9는 0.5ULS 하중조건에서 양방향 반복수평하중이 10회(Ncycle=10) 반복되었을 때, ±1MN, ±3MN, ± 5MN의 하중[여기서 양수 (+)는 전진방향, 음수 (-)는 후진방향을 의미]에서 깊이방향으로 모노파일에 발생하는 최대 및 최소 휨모멘트 분포도를 나타낸다. 그 결과, 모노파일에 작용하는 휨모멘트의 크기는 얕은깊이부터 깊이가 증가함에 따라 증가하다가 6m(1D) 위치에서 최댓값이 발현되었다. 또한, 휨모멘트는 반복수평하중의 크기에 따라 증가하였으며, 큰 하중에서 최대 휨모멘트가 뚜렷하게 나타났다. 최대 모멘트 발생 이후 휨모멘트는 깊이가 깊어짐에 따라 점차 감소하였다. 0.5ULS 하중 조건 외에 0.3ULS, 0.8ULS, 1.2ULS의 하중조건에서도 유사하게 지표면으로부터 6m 깊이(1D)에서 휨모멘트의 최댓값이 발현되었으며, 반복하중 재하에 따른 최대 휨모멘트 발현 깊이의 변화는 미미한 것을 확인하였다.
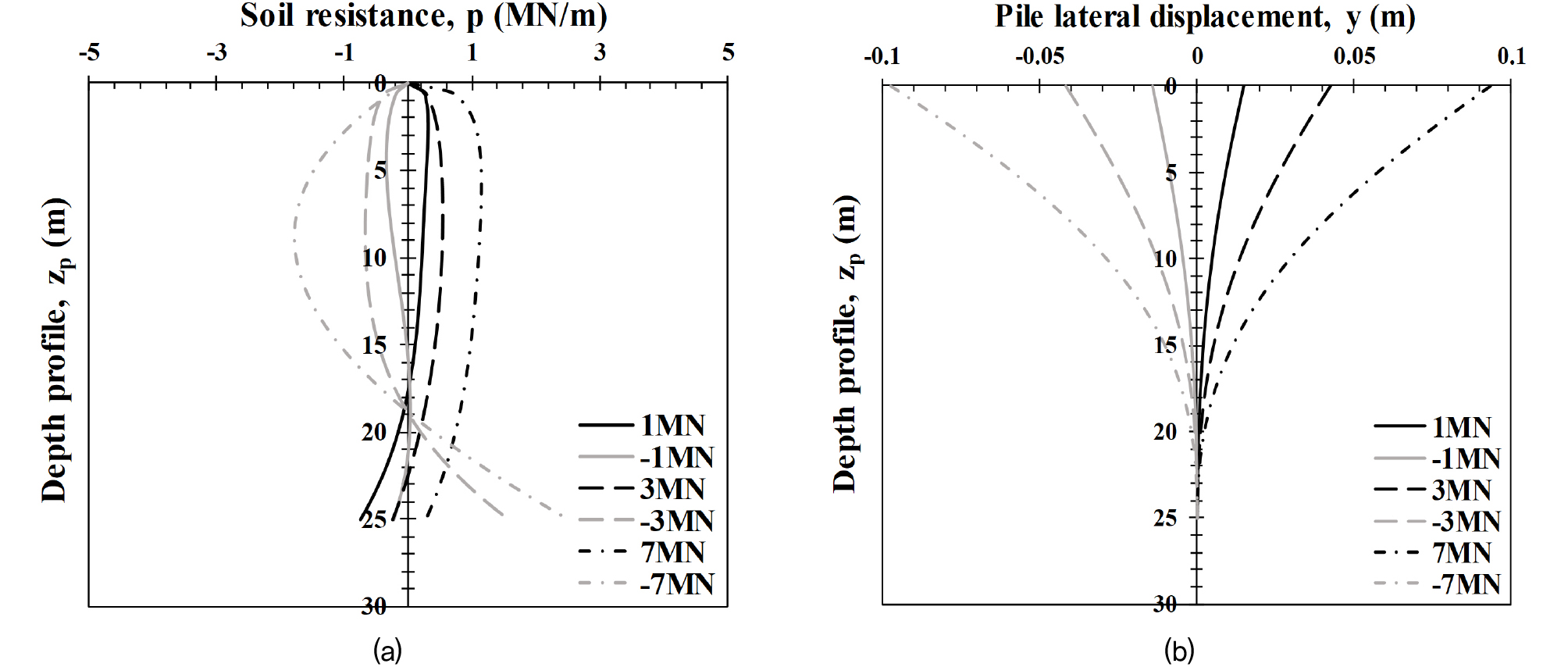
깊이별로 관측된 위치별 모멘트로 도출된 회귀곡선을 이용해 지반반력(p)와 수평변위(y)를 산정하였다. 지반반력은 휨모멘트를 이계미분하여 도출[식 (4)]하였으며, 수평변위는 휨모멘트를 이중적분한 뒤, 모노파일의 휨강성(flexural rigidity, EI)을 나누어 산정하였다[식 (5)]. 이후, 도출된 지반반력과 수평변위를 통해 깊이별 p-y 곡선을 도출하였다. Fig. 10은 위 과정을 통해 획득한 양방향 반복수평하중을 받는 모노파일에 대해 0.8ULS 양방향 하중조건에서 반복하중이 10회(Ncycle=10) 재하되었을 때, 하중크기 별(±1MN, ±3MN, ±7MN) 지반반력(p)과 수평변위(y)를 나타낸다. 여기서, x축의 양수(+)는 모노파일 전진방향으로 재하될 때의 지반반력을 의미하며, 음수(-)는 모노파일이 후진하는 방향으로 재하될 때의 값을 의미한다.
그 결과, 반복수평하중의 크기가 커질수록 최대 지반반력이 크게 나타나는 것을 알 수 있다. 뿐만 아니라, 음수(-, 후진) 방향의 지반반력이 양수 (+, 전진) 방향의 지반반력보다 더 큰 경향을 확인할 수 있다(Fig. 10a). 이는 최초 하중재하방향인 전진(+)으로 모노파일이 이동하면서 후진방향(-)의 모노파일과 지반사이에 유격이 발생하여 지반이 일부 유입되며, 이후 후진방향(-)으로 하중이 재하되면서 인근 지반이 압축(조밀)되어 발생하는 현상으로 판단된다. 한편, 반복수평하중의 크기가 커질수록 수평변위가 증가하는 경향을 확인할 수 있다(Fig. 10b).
여기서, = 지반반력, = 전단력, = 깊이, = 휨모멘트
여기서, = 처짐각, = 모노파일의 휨강성(flexural rigidity)
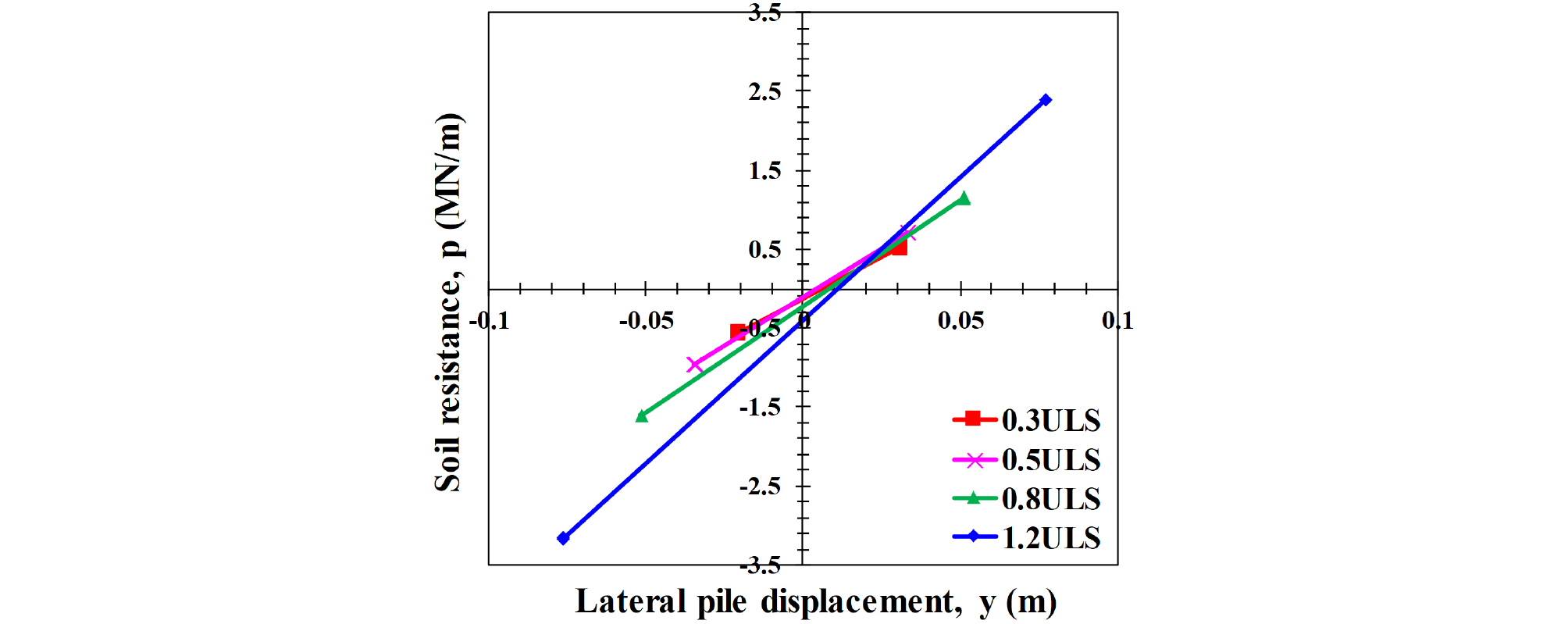
Fig. 11은 반복수평하중을 받는 모노파일의 거동에 대해 반복하중이 20회(Ncycle=20) 재하되었을 때, 1D 깊이(여기서 D는 모노파일 직경)에서 반복하중의 최대값에 대한 p-y 곡선을 나타낸다. 그 결과, 반복수평하중의 크기가 커질수록 동일 변위에서 지반반력이 증가하는 경향을 확인하였다. 이는 낮은 하중(0.3ULS)에서부터 높은 하중(1.2ULS)까지 단계적으로 반복하중이 재하되면서 모노파일 인접지반이 조밀해지기 때문인 것으로 판단된다. 또한, 3사분면의 지반반력(음수 방향)이 1사분면의 지반반력(양수 방향)보다 더 큰 현상을 확인할 수 있다. 이는 Fig. 10a와 같이 모노파일에 최초 수평하중 재하 시 후진방향 (-)으로 지반이 먼저 압축되기 때문이라고 판단된다.
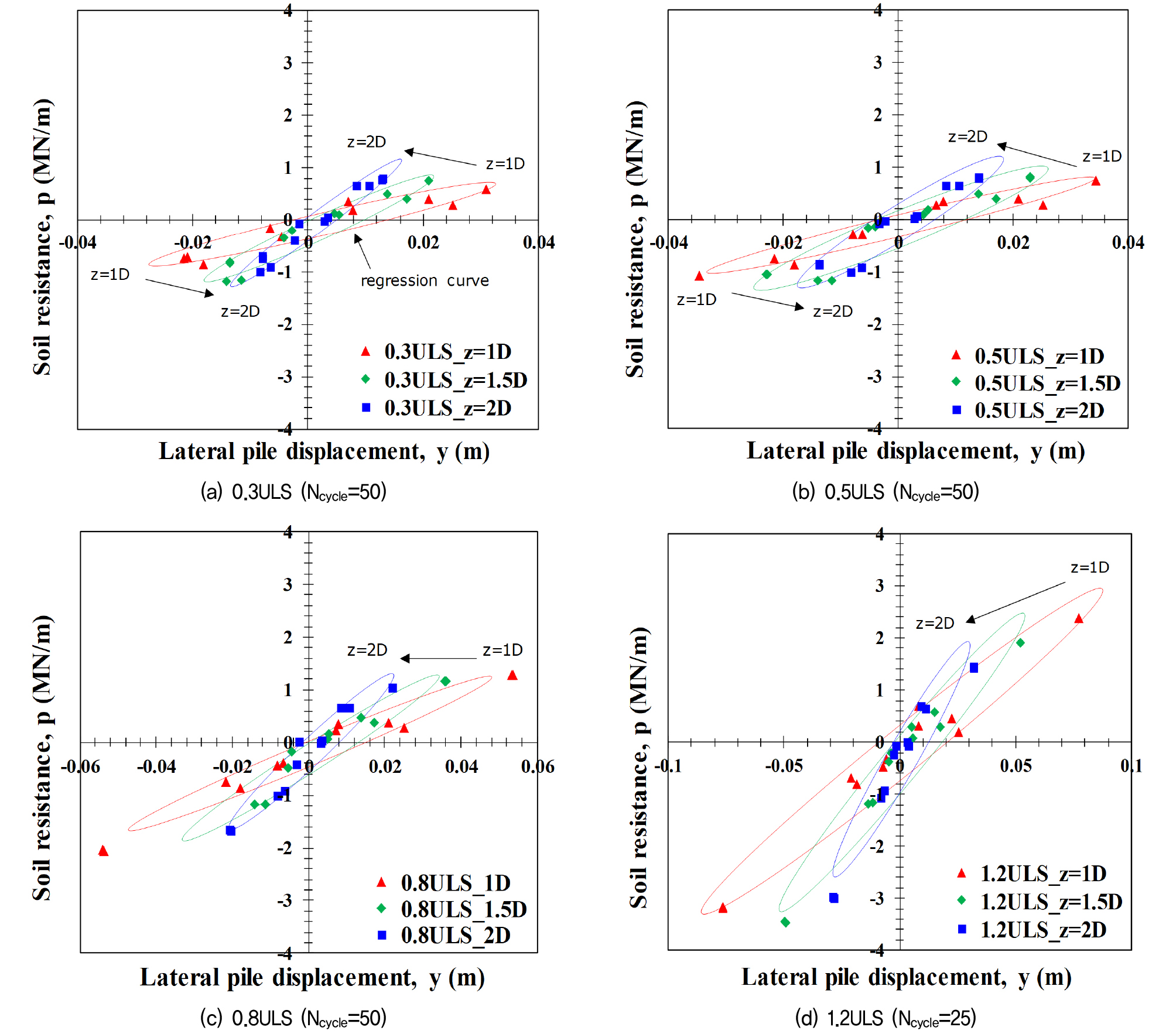
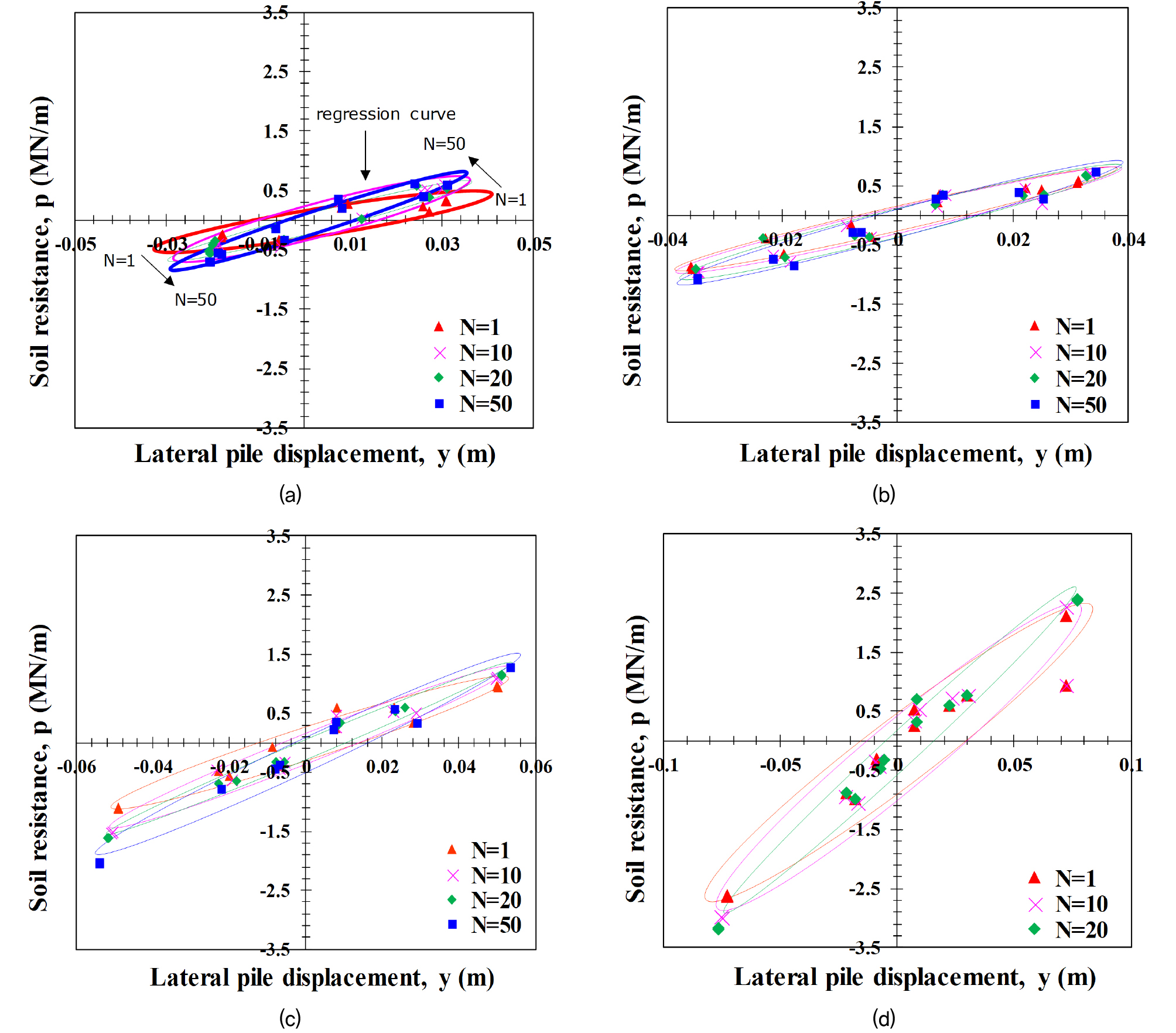
Fig. 12는 반복하중 크기에 따른 깊이별(1D, 1.5D, 2D) p-y 곡선을 나타낸다. 여기서 각 그래프의 표식은 관측값을 나타내며, 타원형 곡선(실선)은 관측값을 토대로 추정한 회귀곡선(regression curve)을 나타낸다. 해석 결과, 지반의 깊이가 깊어질수록 p-y 곡선의 지반반력이 증가하는 경향을 확인하였다(Fig. 12a,b). 이는 지반의 깊이가 깊어질수록 탄성계수 및 구속압의 증가로 인해 지반반력이 증가하기 때문이다. 그러나 Fig. 12d와 같이 1.2ULS에서는 지반의 깊이가 깊어질수록 지반반력이 감소하는 현상을 확인하였다. 이는 극한하중보다 큰 반복하중이 작용하면서 모노파일의 인접지반이 파괴되어 지반반력이 감소했기 때문이라고 판단된다.
Fig. 13은 반복수평하중을 받는 모노파일에 대해 1D 깊이(여기서 D는 모노파일 외경)에서 반복하중 횟수(Ncycle)가 1, 10, 20, 50일 때 p-y 곡선을 나타낸다. p-y 곡선에서 표식은 각 반복수평하중 재하횟수에서 도출된 p-y 값이며, 타원형 이력곡선은 마찬가지로 관측값을 통해 회귀분석하여 도출한 곡선이다. 실험 결과, 반복하중이 최초로 재하되는 0.3ULS에서는 반복하중 횟수가 증가할수록 p-y 곡선의 지반반력이 증가하는 현상을 확인하였다. 특히, 반복횟수가 10회 반복된 시점에서의 p-y 곡선이 크게 변화하는 것을 알 수 있는데, 이는 하중 초기단계에서 인접지반이 조밀해져 나타나기 때문으로 판단된다.
반면, 0.5ULS, 0.8ULS, 1.2ULS 하중 수준에서는 p-y 곡선의 변화가 두드러지지 않았다. 본 연구는 작은 하중(0.3ULS)부터 큰 하중(1.2ULS)까지 단계별로 재하하는 stage 실험으로 수행되었다. 따라서, 단계별로 하중이 점차 커지므로 하중이력에 대한 영향은 미미할 것으로 판단된다. 다만, 첫 하중(0.3ULS)의 경우, 모형 모노파일 설치 후 최초로 재하되는 하중이기 때문에 다른 하중단계에서의 거동과 다소 차이를 보인 것으로 판단된다. 주목할 만한 점은 극한하중에 30% 수준(fatigue limit state, FLS)의 하중이 작용하더라도 하중 반복에 따른 p-y 곡선에 큰 변화가 발생한다는 점이다. 이러한 현상은 느슨한 실트질 모래 지반이 낮은 크기의 반복하중에서 인접지반에 다짐효과가 발생하여 하중재하 초기부터 조밀해졌기 때문으로 판단된다. 즉, 느슨한 실트질 모래지반에서 양방향 반복하중 재하 시 비교적 낮은 하중에서도 10회 이하의 반복하중으로 인한 p-y 곡선의 크기가 크게 변화함을 의미한다. 이러한 현상은 선행연구인 Baek et al.(2019)에서도 유사하게 나타난다.
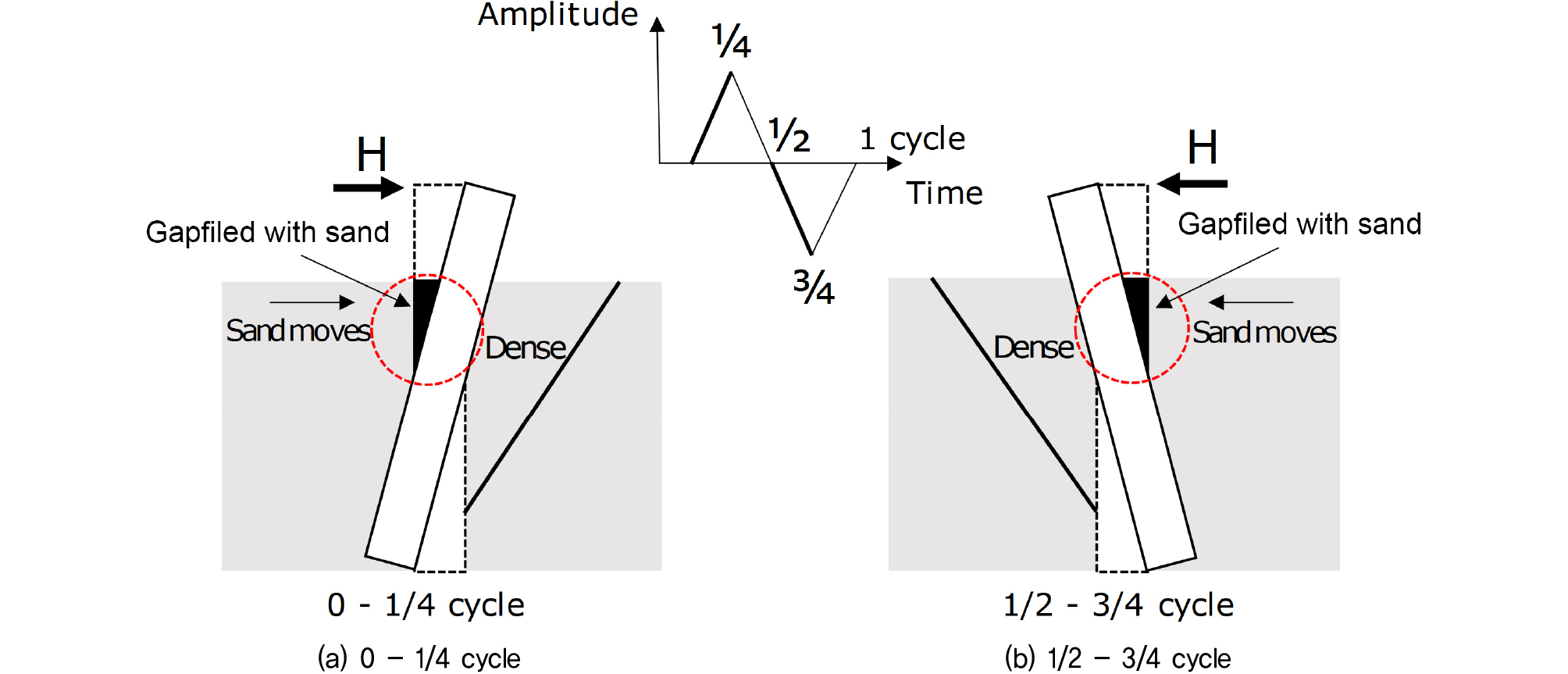
또한, 양방향 반복하중에 대해 모노파일의 전진방향(forward direction, 양수(+))보다 반대 방향인 후진방향(backward direction, 음수(-))의 지반반력이 더 크게 증가하는 현상을 확인할 수 있다. 이는 양방향 반복하중이 재하될 때 최초 반복하중재하 방향의 반대 방향 지반이 일부 붕괴되면서 수평하중에 의한 변위가 발생하는 만큼 빈틈을 메웠다가 반대방향으로 하중이 재하되면서 다져져 위치별 지반반력에 차이가 발생한 것으로 판단된다(Paik et al., 2011). 이는 Fig. 14와 같이 양방향 반복수평하중을 받는 모노파일 인접지반의 거동을 통해 유추할 수 있다. 즉, 모노파일 반복하중 재하 초기에 모노파일이 전진방향(0~1/4 주기)으로 이동하면서 후면에 발생하는 빈틈에 모래가 유입되고, 이후 모노파일이 후진방향으로 이동(1/2~3/4 주기)하면서 유입된 모래와 모노파일에 작용하는 하중에 의해 지반이 조밀해진다. 이로 인해 양방향 반복하중에 불균형이 발생하는 것으로 판단된다.
3.3 p-y 곡선 비교
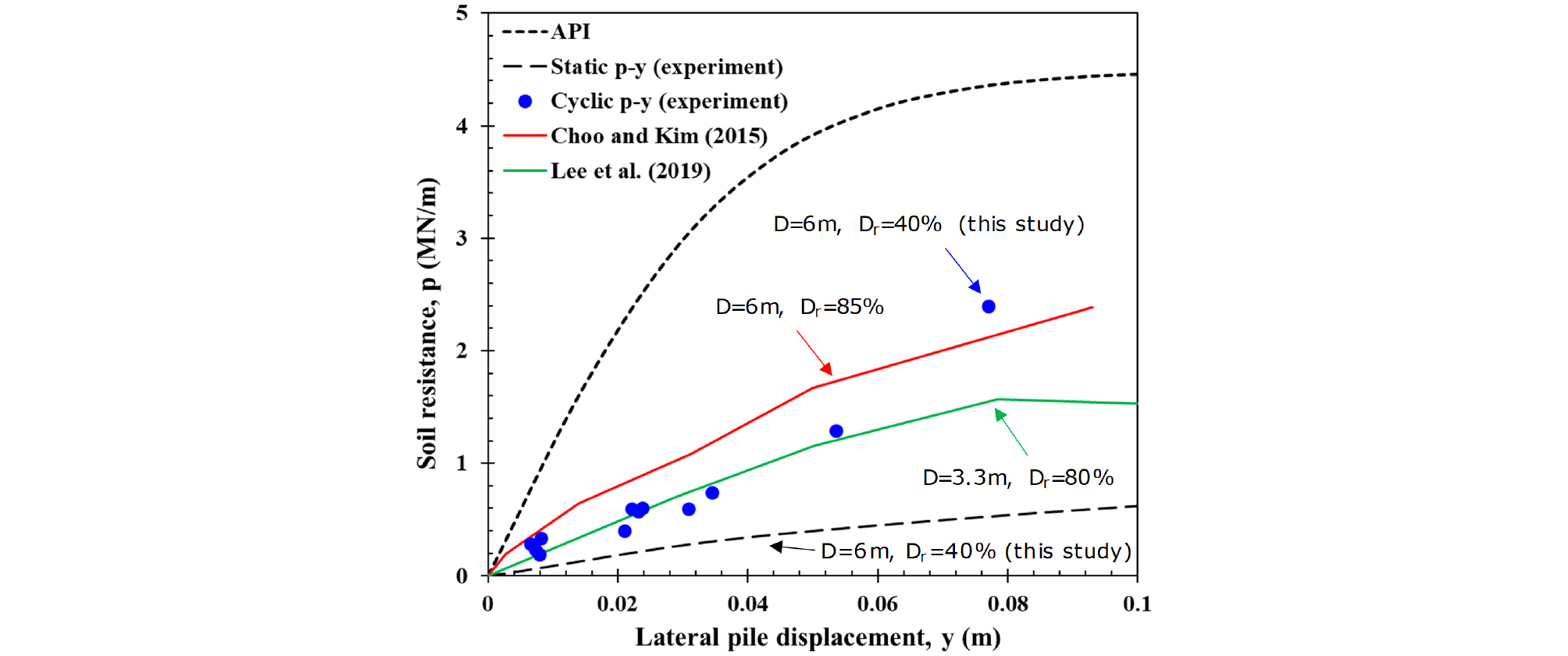
Fig. 15는 원심모형실험을 통해 도출된 p-y 곡선을 나타낸다. Fig. 15에서 파란색 원(circle)은 반복수평하중 실험에서 각 하중 단계의 마지막 하중에 대한 결과(0.3ULS 하중 100회, 0.5ULS하중 50회, 0.8ULS하중 50회, 1.2ULS하중 25회)를 나타내는데, 정적하중재하 실험에 비해 약 3.18~6배 큰 값을 나타내었다. 이는 앞서 언급한 바와 같이 반복수평하중 재하로 인해 느슨한 실트질 모래지반이 조밀해지기 때문으로 판단된다. 한편, API p-y 곡선이 양방향 반복하중재하 실험을 통해 도출된 p-y 곡선보다 약 1.77~4.54배 큰 값을 나타냈으며, 정적하중 p-y 곡선보다는 약 10~14.45배 큰 값을 나타내었다. 이는 현행 API p-y 곡선이 실트질 모래지반에서 대구경 모노파일의 수평거동에 대한 지반반력을 과대평가하고 있음을 의미한다.
또한, API p-y 곡선은 직경 1m 미만 소구경 말뚝의 현장시험을 기반으로 제안되었기 때문에 모노파일과 같은 대구경 말뚝과의 차이가 발생한 것으로 판단된다. 즉, 부재에 발생하는 휨모멘트의 크기는 같으나 직경 차이에 의해 지반에서 작용하는 총 지반반력에는 차이가 발생한다. 결과적으로, 현행 API p-y 곡선은 실트질 모래지반에 설치된 대구경 모노파일에 적용하는데 한계가 있음을 확인할 수 있다(Alderlieste et al., 2011; Baek et al., 2019; Choo and Kim, 2015; Hearn et al., 2010).
선행연구와의 비교를 위해 직경 6m를 대상으로 도출한 선행연구결과인 Choo and Kim(2015)의 p-y 곡선을 Fig. 15에 함께 도시하였다. 그 결과, Choo and Kim(2015)의 결과에 비해 본 연구결과가 다소 낮은 p-y 곡선을 나타냈다. 이는 Choo and Kim(2015)이 상대적으로 조밀한 지반에서 실험이 수행되었기 때문으로 판단된다. 한편, 직경 3.3m 소구경 모노파일의 반복수평하중에 대한 원심모형실험 기존연구사례인 Lee et al.(2019)의 p-y 곡선은 본 연구의 p-y 곡선과 유사하게 나타났다. 소구경 모노파일임에도 불구하고, 본 실험과 유사한 현상을 보인 것은 Lee et al.(2019)의 원심모형실험 모형지반이 상대밀도 80%의 매우 조밀한 건조 모래지반에서 하중제어로 수행되었기 때문이라고 판단된다. 본 연구에서 제시한 p-y 곡선은 선행연구들과 직경 및 지반조건이 상이하므로, 모노파일의 p-y 곡선은 반복하중 특성, 지반조건, 모노파일의 직경에 크게 영향을 받을것으로 판단되며, 모노파일 설계 시 구조물 제원과 현장여건을 고려한 p-y 곡선을 활용하는 것이 필요하다.
4. 결 론
본 연구에서는 원심모형실험을 활용해 느슨한 포화 실트질 모래지반에서 직경 6m의 모노파일에 대한 정적하중재하 실험과 양방향 반복하중재하 실험을 수행하였다. 실험을 통해 대구경 모노파일의 장기반복하중에 대한 거동을 실험적으로 평가하였으며, 반복하중에 대한 p-y 곡선을 도출하였다. 본 연구를 통해 얻은 결과는 다음과 같다.
(1) 양방향 반복하중의 크기가 커질수록 p-y 곡선의 지반반력(p)과 수평변위(y)가 증가하는 현상을 확인하였다. 이는 반복하중의 크기가 커질수록 지반반력이 증가하기 때문으로 판단된다.
(2) 극한하중보다 작은 크기의 반복하중(<ULS)에 대한 p-y 곡선은 깊이가 깊어질수록 지반반력이 증가하는 경향을 보였다. 이는 지반의 깊이가 깊어질수록 탄성계수 및 구속응력이 증가하기 때문으로 판단된다.
(3) 극한하중 이상의 반복하중(1.2ULS)에서는 깊이에 따라 지반반력이 점차 감소하였다. 이는 극한하중을 초과한 하중 재하 시 지반이 파괴되어 지반반력이 감소되기 때문으로 판단된다.
(4) 최초로 재하되는 반복하중(0.3ULS)에서 반복하중횟수(Ncycle)가 증가할수록 p-y 곡선의 지반반력이 증가하는 경향을 보였지만 이후 반복하중(0.5ULS, 0.8ULS, 1.2ULS)에서는 증가량이 미미하였다. 특히 0.3ULS 하중이 10회 이하로 작용했을 때 큰 변화가 발생하는 것을 확인하였다.
(5) 양방향 반복하중이 재하되는 경우, p-y 곡선은 모노파일이 전진되는 방향(양수, +)보다 후진하는 방향(음수, -)에서의 지반반력이 크다. 이는 최초 반복하중 재하 시 모노파일과 지반 사이에 발생하는 유격으로 지반이 유입되어 조밀화되기 때문이다.
(6) 본 연구을 통해 도출된 실험 p-y 곡선을 현행 API p-y 곡선 및 선행연구사례와 함께 비교해 본 결과, API p-y 곡선이 초기기울기 및 지반반력을 과대평가하고 있는 것을 확인하였다. 뿐만 아니라, p-y 곡선은 하중방향, 지반조건, 모노파일 제원에 따라 달라짐을 알 수 있다.
본 연구는 비교적 느슨한 지반조건에서 수행되었으므로 조밀한 실트질 모래지반에서의 거동과는 상이할 것으로 예상된다. 뿐만 아니라 변위제어 조건의 하중재하방식 또한 실험결과에 영향을 미쳤을 것으로 판단된다. 따라서, 본 연구결과는 지반조건과 실험조건에 국한할 필요가 있다.